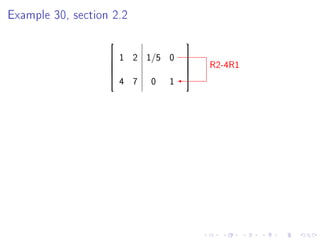
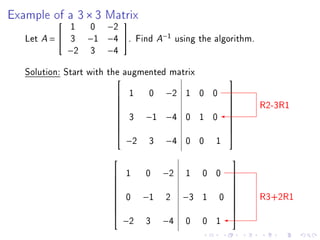
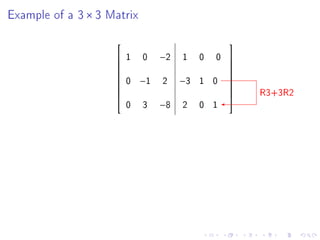
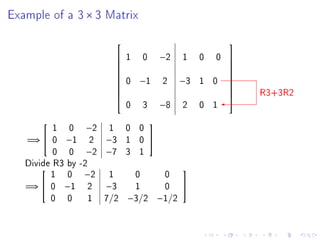
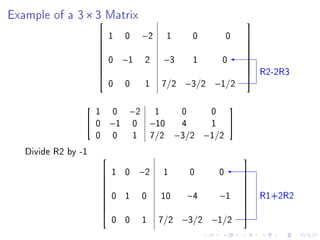
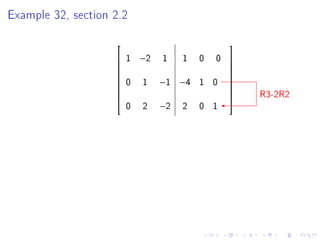
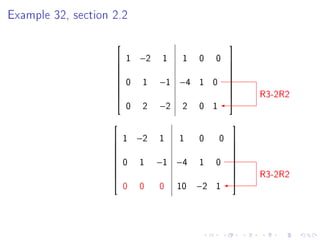
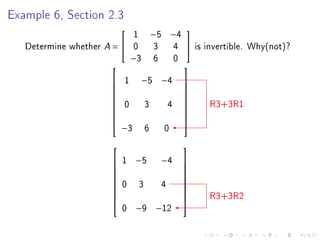
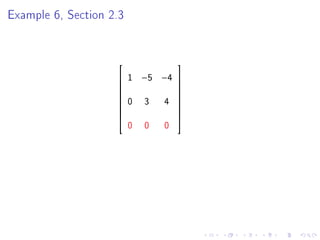
Quiz 2 will be held on January 27 covering sections 1.4, 1.5, 1.7, and 1.8. Test 1 is scheduled for February 1. The document then provides steps to find the inverse of a 2x2 matrix, discusses invertibility if the determinant is 0, and gives an example of finding the inverse of a 3x3 matrix using row reduction of the augmented matrix.

1. Announcements
Quiz 2 on Wednesday Jan 27 on sections 1.4, 1.5, 1.7 and 1.8
Test 1 will be on Feb 1, Monday in class. More details later.

2. Last Class
a b
Let A = . If ad − bc = 0 then A is invertible and
c d
−1 1 d −b
A =
ad − bc −c a
.

3. Last Class
a b
Let A = . If ad − bc = 0 then A is invertible and
c d
−1 1 d −b
A =
ad − bc −c a
.
So if the determinant of A (or det A) is equal to 0, A−1 does not
exist.

4. Last Class
Steps for a 2 × 2 matrix A
1. First check whether det A=0. If so, stop. A is not invertible.

5. Last Class
Steps for a 2 × 2 matrix A
1. First check whether det A=0. If so, stop. A is not invertible.
2. If det A = 0, swap the main diagonal elements of A.

6. Last Class
Steps for a 2 × 2 matrix A
1. First check whether det A=0. If so, stop. A is not invertible.
2. If det A = 0, swap the main diagonal elements of A.
3. Then change the sign of both o diagonal elements (don't
swap these)

7. Last Class
Steps for a 2 × 2 matrix A
1. First check whether det A=0. If so, stop. A is not invertible.
2. If det A = 0, swap the main diagonal elements of A.
3. Then change the sign of both o diagonal elements (don't
swap these)
4. Divide this matrix (after steps 2 and 3) by detA to give A−1 .
(This divides each element of the resultant matrix.)
5. If you want to check your answer, you can see whether
1 0
AA−1 =
0 1
6. This method will not work for 3 × 3 or bigger matrices.

8. Example 7(a) section 2.2, One Case
1 2
Let A = . Find A−1 and use it to solve the equation
5 12
2
Ax = b3 where b3 =
6
Solution: Here detA = (1)(12) − (5)(2) = 2 = 0. So we can nd A−1 .

9. Example 7(a) section 2.2, One Case
1 2
Let A = . Find A−1 and use it to solve the equation
5 12
2
Ax = b3 where b3 =
6
Solution: Here detA = (1)(12) − (5)(2) = 2 = 0. So we can nd A−1 .
Interchange the positions of 1 and 12. Change the signs of 2 and 5.
Then we get
12 −2
−5 1
.

10. Example 7(a) section 2.2, One Case
1 2
Let A = . Find A−1 and use it to solve the equation
5 12
2
Ax = b3 where b3 =
6
Solution: Here detA = (1)(12) − (5)(2) = 2 = 0. So we can nd A−1 .
Interchange the positions of 1 and 12. Change the signs of 2 and 5.
Then we get
12 −2
−5 1
. Divide each element of the matrix by detA which is 2. This gives
−1 6 −1
A =
−5/2 1/2
x1 6 −1 2 6
x= = =
x2 −5/2 1 /2 6 −2
A−1 b

11. Algorithm to nd A−1
To nd the inverse of a square matrix A of any size,
1. Write the augmented matrix with A and I (the identity matrix
of proper size) written side by side.

12. Algorithm to nd A−1
To nd the inverse of a square matrix A of any size,
1. Write the augmented matrix with A and I (the identity matrix
of proper size) written side by side.
2. Do proper row reductions on both A and I till A is reduced to
I.

13. Algorithm to nd A−1
To nd the inverse of a square matrix A of any size,
1. Write the augmented matrix with A and I (the identity matrix
of proper size) written side by side.
2. Do proper row reductions on both A and I till A is reduced to
I.
3. This changes I to a new matrix which is A−1

14. Algorithm to nd A−1
To nd the inverse of a square matrix A of any size,
1. Write the augmented matrix with A and I (the identity matrix
of proper size) written side by side.
2. Do proper row reductions on both A and I till A is reduced to
I.
3. This changes I to a new matrix which is A−1
4. If you cannot reduce A to I (if you get a row full of zeros for
example), A−1 does not exist

15. Example 30, section 2.2
5 10
Let A = . Find A−1 using the algorithm.
4 7
Solution: Start with the augmented matrix
 


5 10 1 0 

 
4 7 0 1
 

16. Example 30, section 2.2
5 10
Let A = . Find A−1 using the algorithm.
4 7
Solution: Start with the augmented matrix
 


5 10 1 0 

 
4 7 0 1
 
Divide R1 by 5  


1 2 1/5 0 

 
4 7 0 1
 

17. Example 30, section 2.2
 
1 2 1/5 0
R2-4R1
 
 
 
4 7 0 1
 

18. Example 30, section 2.2
 
1 2 1/5 0
R2-4R1
 
 
 
4 7 0 1
 
 
1 2 1/5 0
R1+2R2
 
 
 
0 −1 −4/5 1
 
1 0 −7/5 2
=⇒
0 −1 −4/5 1

19. Example 30, section 2.2
 
1 2 1/5 0
R2-4R1
 
 
 
4 7 0 1
 
 
1 2 1/5 0
R1+2R2
 
 
 
0 −1 −4/5 1
 
1 0 −7/5 2
=⇒
0 −1 −4/5 1
1 0 −7/5 2
Divide R2 by -1 =⇒ = I A−1
0 1 4/5 −1

20. Example of a 3 × 3 Matrix
1 0 −2
 
Let A =  3 −1 −4 . Find A−1 using the algorithm.
−2 3 −4
Solution: Start with the augmented matrix

21. Example of a 3 × 3 Matrix
1 0 −2
 
Let A =  3 −1 −4 . Find A−1 using the algorithm.
−2 3 −4
Solution: Start with the augmented matrix
 
 1 0 −2 1 0 0 
R2-3R1
 
 
3 −1 −4 0 1 0
 
 
 
 
−2 3 −4 0 0 1
 
 
 1 0 −2 1 0 0 
 
 
0 −1 2 −3 1 0 R3+2R1
 
 
 
 
−2 3 −4 0 0 1
 

22. Example of a 3 × 3 Matrix
 
 1 0 −2 1 0 0 
 
 
0 −1 2 −3 1 0
 
 
R3+3R2
 
 
0 3 −8 2 0 1
 

23. Example of a 3 × 3 Matrix
 
 1 0 −2 1 0 0 
 
 
0 −1 2 −3 1 0
 
 
R3+3R2
 
 
0 3 −8 2 0 1
 
1 0 −2 1 0 0
 
=⇒  0 −1 2 −3 1 0 
0 0 −2 −7 3 1
Divide R3 by -2
1 0 −2 1 0 0
 
=⇒  0 −1 2 −3 1 0 
0 0 1 7/2 −3/2 −1/2

24. Example of a 3 × 3 Matrix
 
 1 0 −2 1 0 0 
 
 
0 −1 2 −3 1 0
 
 
R2-2R3
 
 
0 0 1 7 /2 −3/2 −1/2
 
1 0 −2 1 0 0
 
 0 −1 0 −10 4 1 
0 0 1 7 /2 −3/2 −1/2
Divide R2 by -1  
 1 0 −2 1 0 0 
 
 
0 1 0 10 −4 −1 R1+2R2
 
 
 
 
0 0 1 7/2 −3/2 −1/2
 

25. Example of a 3 × 3 Matrix

26. Example of a 3 × 3 Matrix
 
 1 0 0 8 −3 −1 
 
 
0 1 0 10 −4 −1
 
 
 
 
0 0 1 7 /2 −3/2 −1/2
 
= I A−1

27. Example 32, section 2.2
1 −2 1
 
Let A =  4 −7 3 . Find A−1 using the algorithm.
−2 6 −4
Solution: Start with the augmented matrix
 
 1 −2 1 1 0 0 
R2-4R1
 
 
4 −7 3 0 1 0
 
 
 
 
−2 6 −4 0 0 1
 
 
 1 −2 1 1 0 0 
 
 
0 1 −1 −4 1 0 R3+2R1
 
 
 
 
−2 6 −4 0 0 1
 

28. Example 32, section 2.2
 
 1 −2 1 1 0 0 
 
 
0 1 −1 −4 1 0
 
 
R3-2R2
 
 
0 2 −2 2 0 1
 

29. Example 32, section 2.2
 
 1 −2 1 1 0 0 
 
 
0 1 −1 −4 1 0
 
 
R3-2R2
 
 
0 2 −2 2 0 1
 
 
 1 −2 1 1 0 0 
 
 
0 1 −1 −4 1 0
 
 
R3-2R2
 
 
0 0 0 10 −2 1
 

30. Very Important
Conclusion: You cannot reduce A to I because of the zero row and
so A−1 does not exist
1. Here A does not have a pivot in every row.

31. Very Important
Conclusion: You cannot reduce A to I because of the zero row and
so A−1 does not exist
1. Here A does not have a pivot in every row.
2. Here A does not have pivot in every column (there is a free
variable)

32. Very Important
Conclusion: You cannot reduce A to I because of the zero row and
so A−1 does not exist
1. Here A does not have a pivot in every row.
2. Here A does not have pivot in every column (there is a free
variable)
3. The equation Ax = 0 has Non-trivial solution

33. Very Important
Conclusion: You cannot reduce A to I because of the zero row and
so A−1 does not exist
1. Here A does not have a pivot in every row.
2. Here A does not have pivot in every column (there is a free
variable)
3. The equation Ax = 0 has Non-trivial solution
4. The columns of A are linearly

34. Very Important
Conclusion: You cannot reduce A to I because of the zero row and
so A−1 does not exist
1. Here A does not have a pivot in every row.
2. Here A does not have pivot in every column (there is a free
variable)
3. The equation Ax = 0 has Non-trivial solution
4. The columns of A are linearly Dependent

35. Very Important
Conclusion: You cannot reduce A to I because of the zero row and
so A−1 does not exist
1. Here A does not have a pivot in every row.
2. Here A does not have pivot in every column (there is a free
variable)
3. The equation Ax = 0 has Non-trivial solution
4. The columns of A are linearly Dependent
5. A cannot be row-reduced to the 3 × 3 identity matrix

36. Section 2.3 Invertible Matrices
If a square matrix A of size n × n is invertible the following is true

37. Section 2.3 Invertible Matrices
If a square matrix A of size n × n is invertible the following is true
Theorem
The Invertible Matrix Theorem (IMT)
1. A has n pivot positions (n pivot rows and n pivot columns)

38. Section 2.3 Invertible Matrices
If a square matrix A of size n × n is invertible the following is true
Theorem
The Invertible Matrix Theorem (IMT)
1. A has n pivot positions (n pivot rows and n pivot columns)
2. A can be row-reduced to the n × n identity matrix

39. Section 2.3 Invertible Matrices
If a square matrix A of size n × n is invertible the following is true
Theorem
The Invertible Matrix Theorem (IMT)
1. A has n pivot positions (n pivot rows and n pivot columns)
2. A can be row-reduced to the n × n identity matrix
3. The equation Ax = 0 has only the trivial solution (no free
variables)

40. Section 2.3 Invertible Matrices
If a square matrix A of size n × n is invertible the following is true
Theorem
The Invertible Matrix Theorem (IMT)
1. A has n pivot positions (n pivot rows and n pivot columns)
2. A can be row-reduced to the n × n identity matrix
3. The equation Ax = 0 has only the trivial solution (no free
variables)
4. The columns of A are linearly

41. Section 2.3 Invertible Matrices
If a square matrix A of size n × n is invertible the following is true
Theorem
The Invertible Matrix Theorem (IMT)
1. A has n pivot positions (n pivot rows and n pivot columns)
2. A can be row-reduced to the n × n identity matrix
3. The equation Ax = 0 has only the trivial solution (no free
variables)
4. The columns of A are linearly independent

42. Section 2.3 Invertible Matrices
If a square matrix A of size n × n is invertible the following is true
Theorem
The Invertible Matrix Theorem (IMT)
1. A has n pivot positions (n pivot rows and n pivot columns)
2. A can be row-reduced to the n × n identity matrix
3. The equation Ax = 0 has only the trivial solution (no free
variables)
4. The columns of A are linearly independent
5. The equation Ax = b is consistent for every b in Rn

43. Section 2.3 Invertible Matrices
If a square matrix A of size n × n is invertible the following is true
Theorem
The Invertible Matrix Theorem (IMT)
1. A has n pivot positions (n pivot rows and n pivot columns)
2. A can be row-reduced to the n × n identity matrix
3. The equation Ax = 0 has only the trivial solution (no free
variables)
4. The columns of A are linearly independent
5. The equation Ax = b is consistent for every b in Rn
6. The columns of A span Rn (because every row has a pivot and
recall theorem 4, sec 1.4)

44. Example 2, Section 2.3
−4 6
Determine whether A = is invertible. Why(not)?
6 −9

45. Example 2, Section 2.3
−4 6
Determine whether A = is invertible. Why(not)?
6 −9
Solution: Clearly the determinant is (-4)(-9)-(6)(6)=36-36=0. So
not invertible. Checking invertibility of 2 × 2 matrices are thus easy.
Not so obvious fact: The second column is -1.5 times the rst
column. Since we have linearly dependent columns, by IMT, A is
not invertible.

46. Example 4, Section 2.3
−7 0 4
 
Determine whether A =  3 0 −1  is invertible. Why(not)?
2 0 9
Solution: Remember what happens to a set of vectors if the zero
vector is present in that set?

47. Example 4, Section 2.3
−7 0 4
 
Determine whether A =  3 0 −1  is invertible. Why(not)?
2 0 9
Solution: Remember what happens to a set of vectors if the zero
vector is present in that set? The vectors are linearly dependent.
Since the second column of A is full of zeros, we have linearly
dependent columns, and so A is not invertible.

48. Example 6, Section 2.3
1 −5 −4
 
Determine whether A =  0 3 4  is invertible. Why(not)?
−3 6 0
 
 1 −5 −4 
 
 
0 3 4 R3+3R1
 
 
 
 
−3 6 0
 
 
 1 −5 −4 
 
 
0 3 4
 
 
R3+3R2
 
 
0 −9 −12
 

49. Example 6, Section 2.3
 
 1 −5 −4 
 
 
0 3 4 
 

 
 
0 0 0
 

50. Example 6, Section 2.3
 
 1 −5 −4 
 
 
0 3 4 
 

 
 
0 0 0
 
Since the third row (and the third column) does not have a pivot,
we have linearly dependent columns and by the IMT A is not
invertible.

51. Example 8, Section 2.3
1 3 7 4
 
 0 5 9 6 
Determine whether A =  
is invertible. Why(not)?
0 0 2 8
 
 
0 0 0 10

52. Example 8, Section 2.3
1 3 7 4
 
 0 5 9 6 
Determine whether A =  
is invertible. Why(not)?
0 0 2 8
 
 
0 0 0 10
Solution: This matrix is already in the echelon form. There are 4
pivot rows and 4 pivot columns. So A is invertible.