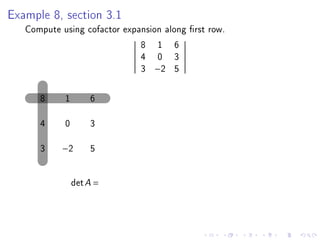
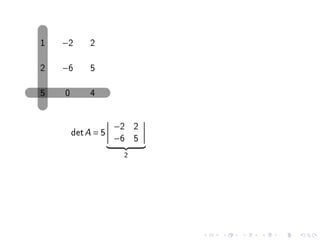
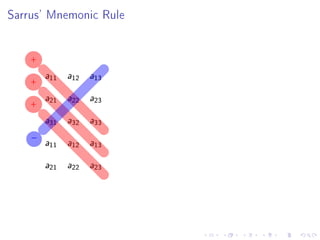
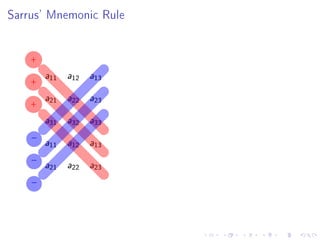
The document contains announcements and information about an exam for a class. It includes the following key points: - Students should bring any grade-related questions about Exam 1 without delay. The homework for Exam 2 has been uploaded. - The professor is planning to cover chapters 3, 5, and 6 for Exam 2. - The last day for students to drop the class with a grade of "W" is February 4th.

1. Announcements
Please bring any grade related questions regarding exam 1
without delay.
Homework set for exam 2 has been uploaded. Please check it
often, I may make small inclusions/exclusions.
Planning to do parts of chapters 3, 5 and 6 for exam 2.
Last day to drop this class with grade "W" is Feb 4.

2. Section 3.1 Introduction to Determinants
1. A 2 × 2 matrix A is invertible if and only if det A= 0.

3. Section 3.1 Introduction to Determinants
1. A 2 × 2 matrix A is invertible if and only if det A= 0.
2. We can now extend this idea to a 3 × 3 or larger matrices.

4. Section 3.1 Introduction to Determinants
1. A 2 × 2 matrix A is invertible if and only if det A= 0.
2. We can now extend this idea to a 3 × 3 or larger matrices.
3. Determinants exist only for square matrices.
Notation The notation aij means the element in the i -th row and
j -th column of a matrix.

5. Section 3.1 Introduction to Determinants
1. A 2 × 2 matrix A is invertible if and only if det A= 0.
2. We can now extend this idea to a 3 × 3 or larger matrices.
3. Determinants exist only for square matrices.
Notation The notation aij means the element in the i -th row and
j -th column of a matrix.
So a23 means the element in the second row, third column of a
given matrix.

6. Determinant of a 2 × 2 matrix
You know this one!!

7. Determinant of a 2 × 2 matrix
You know this one!!
If
a11 a12
A =
a21 a22
Here, det A =a11 a22 − a21 a12 . It is a number.

8. What about a 3 × 3 matrix?
If  
a11 a12 a13
A = a21 a22 a23 
a31 a32 a33

9. What about a 3 × 3 matrix?
If  
a11 a12 a13
A = a21 a22 a23 
a31 a32 a33
We have to break this down to multiple 2 × 2 determinants.

10. What about a 3 × 3 matrix?
You can start the computation using any row or column as an
anchor.

11. What about a 3 × 3 matrix?
You can start the computation using any row or column as an
anchor.
Suppose you choose the rst row.
Each entry of the rst row will give one term each as follows.

12. What about a 3 × 3 matrix?
You can start the computation using any row or column as an
anchor.
Suppose you choose the rst row.
Each entry of the rst row will give one term each as follows.
Add the terms at the end to get det A.

13. What about a 3 × 3 matrix?
You can start the computation using any row or column as an
anchor.
Suppose you choose the rst row.
Each entry of the rst row will give one term each as follows.
Add the terms at the end to get det A.
To get the rst term of det A, cover the row and column
corresponding to a11 .

14. What about a 3 × 3 matrix?
You can start the computation using any row or column as an
anchor.
Suppose you choose the rst row.
Each entry of the rst row will give one term each as follows.
Add the terms at the end to get det A.
To get the rst term of det A, cover the row and column
corresponding to a11 .
a11 a12 a13
a21 a22 a23
a31 a32 a33

15. Multiply a11 with the determinant of the remaining matrix
a22 a23
a32 a33

16. Multiply a11 with the determinant of the remaining matrix
a22 a23
a32 a33
Thus the rst term is (
a11 a22 a33 − a32 a23 ).

17. Multiply a11 with the determinant of the remaining matrix
a22 a23
a32 a33
Thus the rst term is a11 (a22 a33 − a32 a23 ).
To get the second term of det A, cover the row and column
corresponding to a12 .
a11 a12 a13
a21 a22 a23
a31 a32 a33

18. Multiply a11 with the determinant of the remaining matrix
a22 a23
a32 a33
Thus the rst term is a11 (a22 a33 − a32 a23 ).
To get the second term of det A, cover the row and column
corresponding to a12 .
a11 a12 a13
a21 a22 a23
a31 a32 a33
Multiply the negative of a12 with the determinant of the
remaining matrix
a21 a23
a31 a33

19. Thus the second term is −a12 (a21 a33 − a31 a23 ).

20. Thus the second term is −a12 (a21 a33 − a31 a23 ).
To get the third term of det A, cover the row and column
corresponding to a13 .
a11 a12 a13
a21 a22 a23
a31 a32 a33

21. Thus the second term is −a12 (a21 a33 − a31 a23 ).
To get the third term of det A, cover the row and column
corresponding to a13 .
a11 a12 a13
a21 a22 a23
a31 a32 a33
Multiply a13 with the determinant of the remaining matrix
a21 a22
a31 a32

22. Thus the second term is −a12 (a21 a33 − a31 a23 ).
To get the third term of det A, cover the row and column
corresponding to a13 .
a11 a12 a13
a21 a22 a23
a31 a32 a33
Multiply a13 with the determinant of the remaining matrix
a21 a22
a31 a32
Thus the second term is (
a13 a21 a32 − a31 a22 ).

23. Add the 3 terms you obtained above
(
a11 a22 a33 − a32 a23 ) − a12 (a21 a33 − a31 a23 ) + a13 (a21 a32 − a31 a22 )
This is det A for a 3 × 3 matrix A.

24. Add the 3 terms you obtained above
(
a11 a22 a33 − a32 a23 ) − a12 (a21 a33 − a31 a23 ) + a13 (a21 a32 − a31 a22 )
This is det A for a 3 × 3 matrix A.
DO NOT try to memorize this as a formula

25. Add the 3 terms you obtained above
(
a11 a22 a33 − a32 a23 ) − a12 (a21 a33 − a31 a23 ) + a13 (a21 a32 − a31 a22 )
This is det A for a 3 × 3 matrix A.
DO NOT try to memorize this as a formula
Remember the steps (all the covering and multiplying games)!!

26. Add the 3 terms you obtained above
(
a11 a22 a33 − a32 a23 ) − a12 (a21 a33 − a31 a23 ) + a13 (a21 a32 − a31 a22 )
This is det A for a 3 × 3 matrix A.
DO NOT try to memorize this as a formula
Remember the steps (all the covering and multiplying games)!!
To nd determinant of a 4 × 4 matrix A, break it down into
four 3 × 3 determinants using the same idea. (more work).
This method works for a square matrix of any size.

27. FAQs

28. FAQs
Which row to choose for anchor? Any row (or column)!!

29. FAQs
Which row to choose for anchor? Any row (or column)!!
Any caveats?? Yes!! Need to make sure that you do proper
sign alternating depending on which row or column you
choose. Keep the following in mind.
 
+ − +
A= − + − 
+ − +

30. FAQs
Which row to choose for anchor? Any row (or column)!!
Any caveats?? Yes!! Need to make sure that you do proper
sign alternating depending on which row or column you
choose. Keep the following in mind.
 
+ − +
A= − + − 
+ − +
So, if you decide to use second column, the rst term will be
negative, the second positive and the third negative. (with
proper covering and multiplying)

31. FAQs
Which row to choose for anchor? Any row (or column)!!
Any caveats?? Yes!! Need to make sure that you do proper
sign alternating depending on which row or column you
choose. Keep the following in mind.
 
+ − +
A= − + − 
+ − +
So, if you decide to use second column, the rst term will be
negative, the second positive and the third negative. (with
proper covering and multiplying)
Choose a row or column with as many zeros as possible.

32. Before we go further..
Notation: Use a pair of vertical lines for determinants.

33. Before we go further..
Notation: Use a pair of vertical lines for determinants.
Example
If
1 2 3
 
A= 4 5 6 
7 8 9
then
1 2 3
det A = 4 5 6
7 8 9

34. Going back to our 3 × 3 matrix
 
a11 a12 a13
A = a21 a22 a23 ,
a31 a32 a33

35. Going back to our 3 × 3 matrix
 
a11 a12 a13
A = a21 a22 a23 ,
a31 a32 a33
we can write
a22 a23 a21 a23 a21 a22
det A = a11 −a12 +a13
a32 a33 a31 a33 a31 a32
C11 C12 C13

36. Going back to our 3 × 3 matrix
 
a11 a12 a13
A = a21 a22 a23 ,
a31 a32 a33
we can write
a22 a23 a21 a23 a21 a22
det A = a11 −a12 +a13
a32 a33 a31 a33 a31 a32
C11 C12 C13
Here C11 , C12 and C13 are called the cofactors of A.

37. Going back to our 3 × 3 matrix
 
a11 a12 a13
A = a21 a22 a23 ,
a31 a32 a33
we can write
a22 a23 a21 a23 a21 a22
det A = a11 −a12 +a13
a32 a33 a31 a33 a31 a32
C11 C12 C13
Here C11 , C12 and C13 are called the cofactors of A.
This method of computing determinants is called cofactor
expansion across rst row.

38. In General..
Theorem

39. In General..
Theorem
1. The determinant of an n ×n matrix A can be computed by
cofactor expansion along any row or column.

40. In General..
Theorem
1. The determinant of an n ×n matrix A can be computed by
cofactor expansion along any row or column.
2. Expansion across the i th row will be
det A = ai 1 Ci 1 + ai 2 Ci 2 + . . . + ain Cin .
Don't forget to take care of proper sign alternations depending
on the row.

41. In General..
Theorem
1. The determinant of an n ×n matrix A can be computed by
cofactor expansion along any row or column.
2. Expansion across the i th row will be
det A = ai 1 Ci 1 + ai 2 Ci 2 + . . . + ain Cin .
Don't forget to take care of proper sign alternations depending
on the row.
3. Expansion across the j th column will be
det A = a1j C1j + a2j C2j + . . . + anj Cnj .
Don't forget to take care of proper sign alternations depending
on the column.

42. Example 2, section 3.1
Compute using cofactor expansion along rst row.
0 5 1
4 −3 0
2 4 1

43. Example 2, section 3.1
Compute using cofactor expansion along rst row.
0 5 1
4 −3 0
2 4 1
Solution:
−3 0
det A = 0
4 1
−3

44. Example 2, section 3.1
Compute using cofactor expansion along rst row.
0 5 1
4 −3 0
2 4 1
Solution:
−3 0 4 0
det A = 0 −5
4 1 2 1
−3 4

45. Example 2, section 3.1
Compute using cofactor expansion along rst row.
0 5 1
4 −3 0
2 4 1
Solution:
−3 0 4 0 4 −3
det A = 0 −5 +1
4 1 2 1 2 4
−3 4 22

46. Example 2, section 3.1
Compute using cofactor expansion along rst row.
0 5 1
4 −3 0
2 4 1
Solution:
−3 0 4 0 4 −3
det A = 0 −5 +1
4 1 2 1 2 4
−3 4 22
= 0 − 20 + 22 = 2

47. Example 2, section 3.1
Compute using cofactor expansion down the second column.
0 5 1
4 −3 0
2 4 1

48. Example 2, section 3.1
Compute using cofactor expansion down the second column.
0 5 1
4 −3 0
2 4 1
0 5 1
Solution: 4 −3 0
2 4 1

49. Example 2, section 3.1
Compute using cofactor expansion down the second column.
0 5 1
4 −3 0
2 4 1
0 5 1
4 0
Solution: 4 −3 0 =⇒ −5 = −20
2 1
4
2 4 1

50. Example 2, section 3.1
0 5 1
4 −3 0
2 4 1

51. Example 2, section 3.1
0 5 1
0 1
4 −3 0 =⇒ −3 =6
2 1
−2
2 4 1

52. Example 2, section 3.1
0 5 1
0 1
4 −3 0 =⇒ −3 =6
2 1
−2
2 4 1
0 5 1
4 −3 0
2 4 1

53. Example 2, section 3.1
0 5 1
0 1
4 −3 0 =⇒ −3 =6
2 1
−2
2 4 1
0 5 1
0 1
4 −3 0 =⇒ −4 = 16.
4 0
−4
2 4 1

54. Example 2, section 3.1
0 5 1
0 1
4 −3 0 =⇒ −3 =6
2 1
−2
2 4 1
0 5 1
0 1
4 −3 0 =⇒ −4 = 16.
4 0
−4
2 4 1
Add these terms, -20+6+16=2.

55. Comments

56. Comments
1. Again, be careful with the alternating signs.

57. Comments
1. Again, be careful with the alternating signs.
2. If you are expanding down the second column, the rst term
will be negative, second positive (but already we have a -3)
and the third negative.

58. Example 8, section 3.1
Compute using cofactor expansion along rst row.
8 1 6
4 0 3
3 −2 5

59. Example 8, section 3.1
Compute using cofactor expansion along rst row.
8 1 6
4 0 3
3 −2 5
8 1 6
4 0 3
3 −2 5
det A =

60. Example 8, section 3.1
Compute using cofactor expansion along rst row.
8 1 6
4 0 3
3 −2 5
8 1 6
4 0 3
3 −2 5
0 3
det A = 8
−2 5
6

61. Example 8, section 3.1
Compute using cofactor expansion along rst row.
8 1 6
4 0 3
3 −2 5
8 1 6 8 1 6
4 0 3 4 0 3
3 −2 5 3 −2 5
0 3 4 3
det A = 8 −1
−2 5 3 5
6 11

62. Example 8, section 3.1
Compute using cofactor expansion along rst row.
8 1 6
4 0 3
3 −2 5
8 1 6 8 1 6 8 1 6
4 0 3 4 0 3 4 0 3
3 −2 5 3 −2 5 3 −2 5
0 3 4 3 4 0
det A = 8 −1 +6
−2 5 3 5 3 −2
6 11 −8
= 48 − 11 − 48 = −11

63. Denition
A square matrix A is a Triangular matrix if the entries above OR
below the main diagonal are ALL zeros

64. Denition
A square matrix A is a Triangular matrix if the entries above OR
below the main diagonal are ALL zeros
Theorem
If A is a triangular matrix, then det A is the product of entries on
the main diagonal of A.

65. Example
If
1 2 377 4 514 6
 

 0 5 69 77 81 9 

 0 0 2 2321 45 88 
A=
 
0 0 0 1 45 76.67

 
0 0 0 0 2 81.63
 
 
0 0 0 0 0 1

66. Example
If
1 2 377 4 514 6
 

 0 5 69 77 81 9 

 0 0 2 2321 45 88 
A=
 
0 0 0 1 45 76.67

 
0 0 0 0 2 81.63
 
 
0 0 0 0 0 1
det A = (1)(5)(2)(1)(2)(1) = 20.

67. Larger Convenient Matrices
1. If you have a 4 × 4 or larger matrix with a row or column
mostly zeros, use that row(column) as the anchor.

68. Larger Convenient Matrices
1. If you have a 4 × 4 or larger matrix with a row or column
mostly zeros, use that row(column) as the anchor.
2. Be careful with the sign alterations.

69. Larger Convenient Matrices
1. If you have a 4 × 4 or larger matrix with a row or column
mostly zeros, use that row(column) as the anchor.
2. Be careful with the sign alterations.
3. Have a sign template of proper size handy.

70. Example 10, section 3.1
Compute the following determinant using least amount of
computation.
1 −2 5 2
0 0 3 0
2 −6 −7 5
5 0 4 4

71. Example 10, section 3.1
Compute the following determinant using least amount of
computation.
1 −2 5 2
0 0 3 0
2 −6 −7 5
5 0 4 4
Use row 2 as the anchor. To be sure about the signs use the
following
+ − + −
− + − +
+ − + −
− + − +

72. Example 10, section 3.1
Compute the following determinant using least amount of
computation.
1 −2 5 2
0 0 3 0
2 −6 −7 5
5 0 4 4
Use row 2 as the anchor. To be sure about the signs use the
following
+ − + −
− + − +
+ − + −
− + − +
Only the cofactor of 3 matters here. It will be negative. Others are
all zero.

73. Slide corrected on Feb 2, 12.00pm
1 −2 5 2
0 0 3 0
2 −6 −7 5
5 0 4 4

74. Slide corrected on Feb 2, 12.00pm
1 −2 5 2
0 0 3 0 1 −2 2
=⇒ −3 2 −6 5
2 −6 −7 5 5 0 4
5 0 4 4

75. Slide corrected on Feb 2, 12.00pm
1 −2 5 2
0 0 3 0 1 −2 2
=⇒ −3 2 −6 5
2 −6 −7 5 5 0 4
5 0 4 4
We can expand along the last row. To be safe, keep the sign
template
+ − +
− + −
+ − +

76. 1 −2 2
2 −6 5
5 0 4
−2 2
det A = 5
−6 5
2

77. 1 −2 2 1 −2 2
2 −6 5 2 −6 5
5 0 4 5 0 4
−2 2 1 2
det A = 5 −0
−6 5 2 5
2 0

78. 1 −2 2 1 −2 2 1 −2 2
2 −6 5 2 −6 5 2 −6 5
5 0 4 5 0 4 5 0 4
−2 2 1 2 1 −2
det A = 5 −0 +4
−6 5 2 5 2 −6
2 0 −2
= 10 + 0 + (−8) = 2
Don't forget to multiply the -3 we had. So the answer is -6.

79. Sarrus' Mnemonic Rule
1. An easy to remember method for 3 × 3 matrices

80. Sarrus' Mnemonic Rule
1. An easy to remember method for 3 × 3 matrices
2. DO NOT apply this method for larger matrices.
3. Make sure all rows and columns are properly aligned, otherwise
it becomes very confusing.

81. Sarrus' Mnemonic Rule
1. An easy to remember method for 3 × 3 matrices
2. DO NOT apply this method for larger matrices.
3. Make sure all rows and columns are properly aligned, otherwise
it becomes very confusing.
4. Start by repeating the rst 2 rows immediately beneath the
determinant.

82. Sarrus' Mnemonic Rule
a11 a12 a13
a21 a22 a23
a31 a32 a33
a11 a12 a13
a21 a22 a23

83. Sarrus' Mnemonic Rule
+
a11 a12 a13
a21 a22 a23
a31 a32 a33
a11 a12 a13
a21 a22 a23

84. Sarrus' Mnemonic Rule
+
a11 a12 a13
+
a21 a22 a23
a31 a32 a33
a11 a12 a13
a21 a22 a23

85. Sarrus' Mnemonic Rule
+
a11 a12 a13
+
a21 a22 a23
+
a31 a32 a33
a11 a12 a13
a21 a22 a23

86. Sarrus' Mnemonic Rule
+
a11 a12 a13
+
a21 a22 a23
+
a31 a32 a33
−
a11 a12 a13
a21 a22 a23

87. Sarrus' Mnemonic Rule
+
a11 a12 a13
+
a21 a22 a23
+
a31 a32 a33
−
a11 a12 a13
−
a21 a22 a23

88. Sarrus' Mnemonic Rule
+
a11 a12 a13
+
a21 a22 a23
+
a31 a32 a33
−
a11 a12 a13
−
a21 a22 a23
−