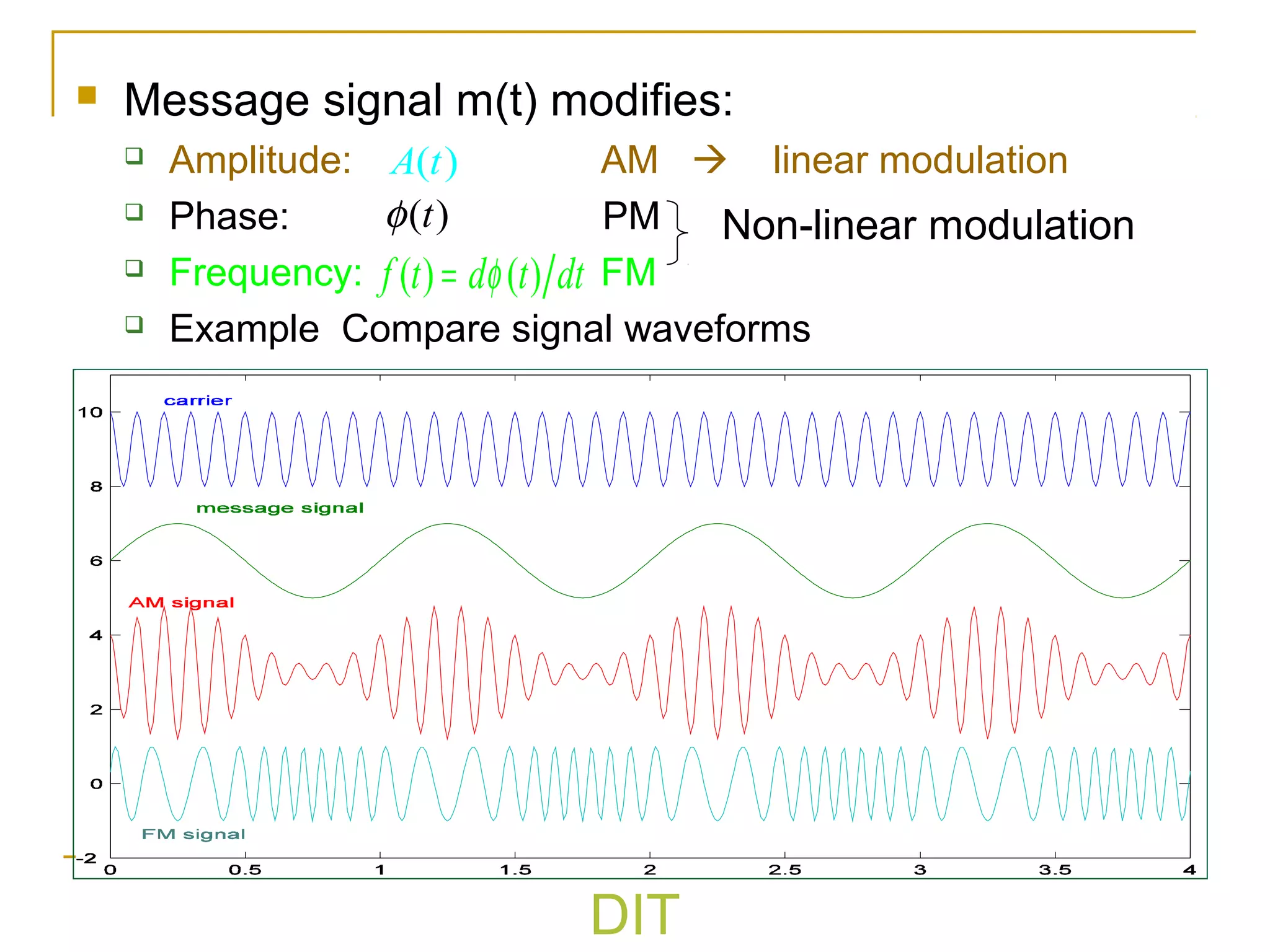
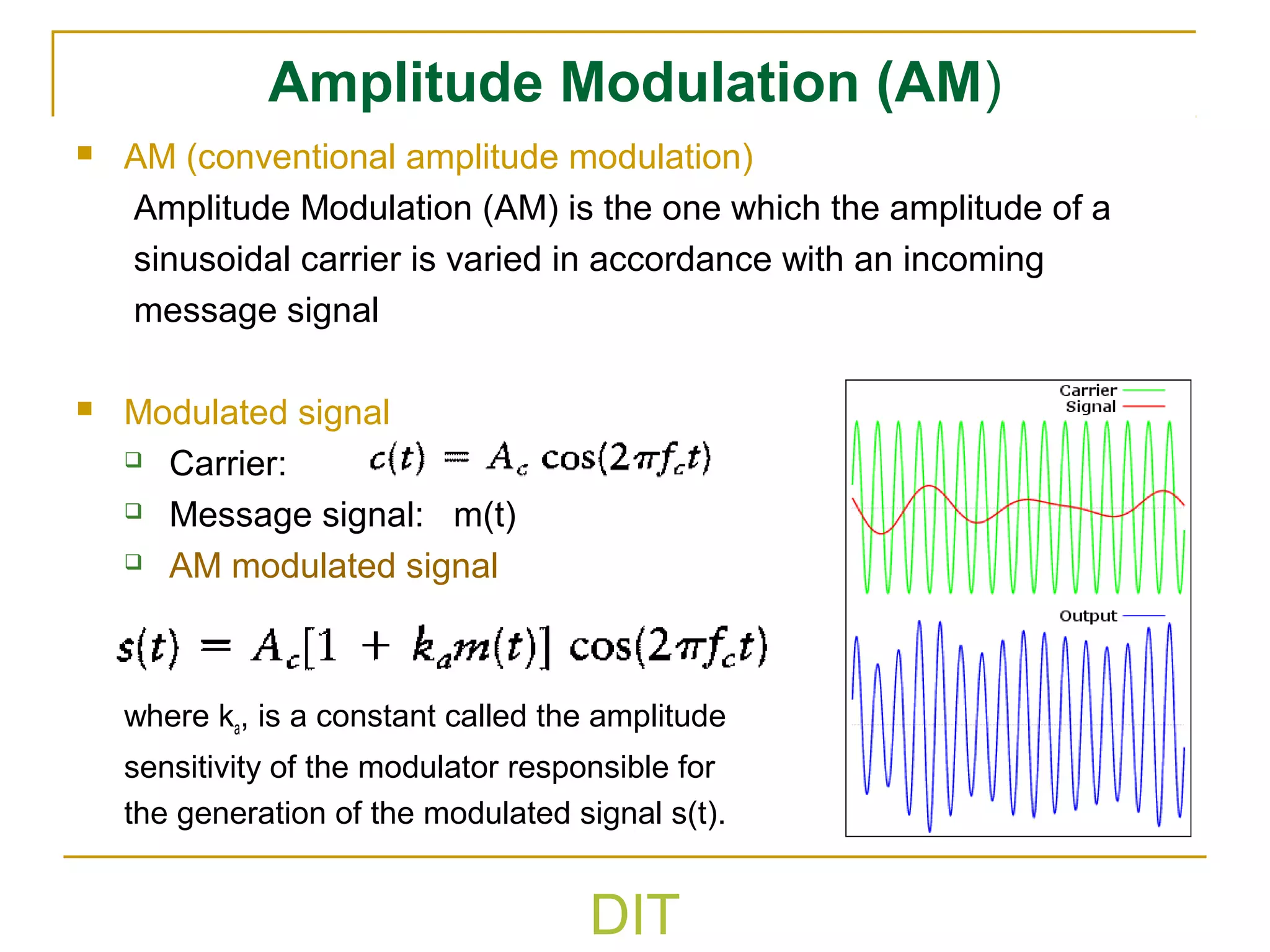
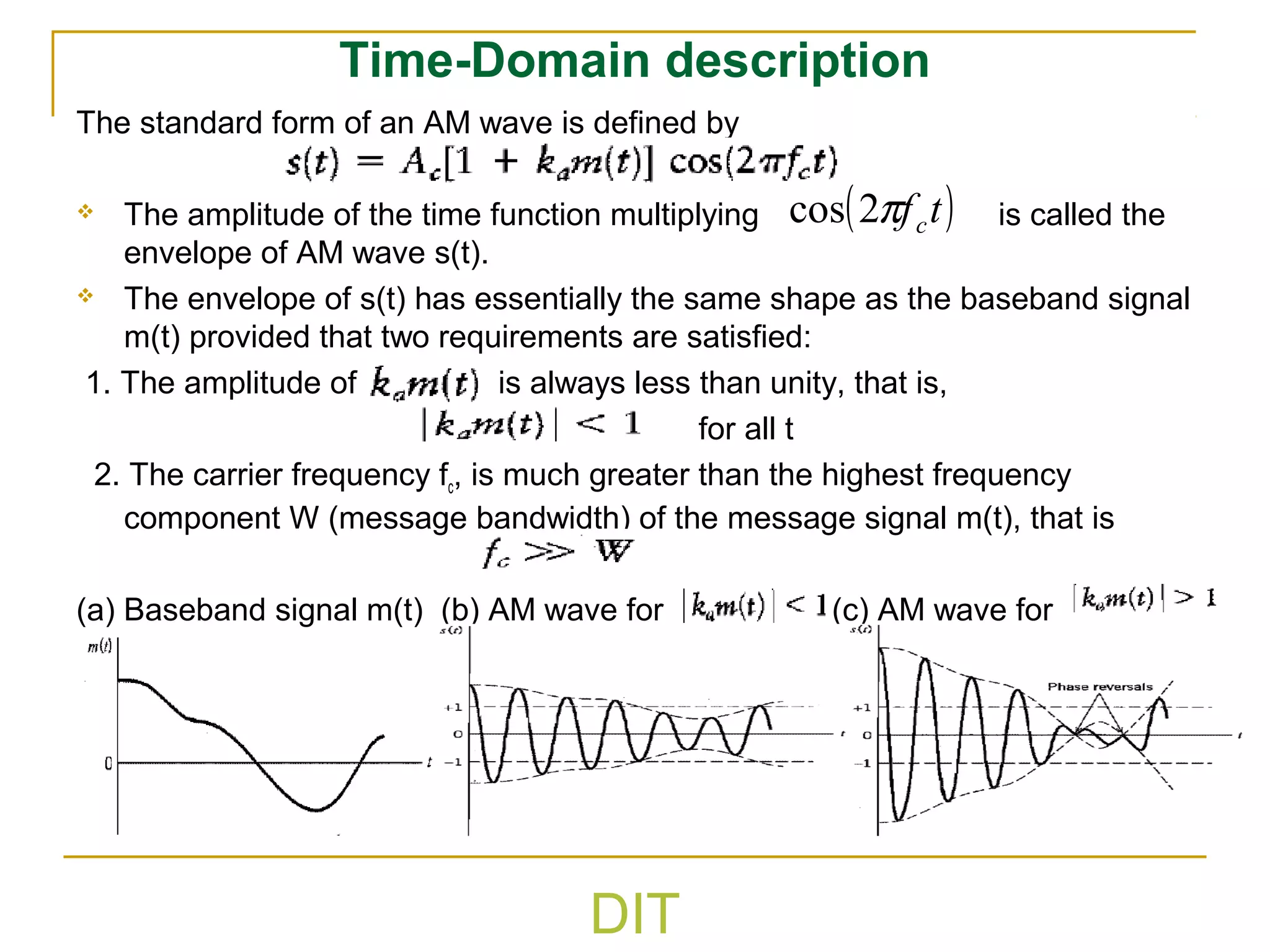
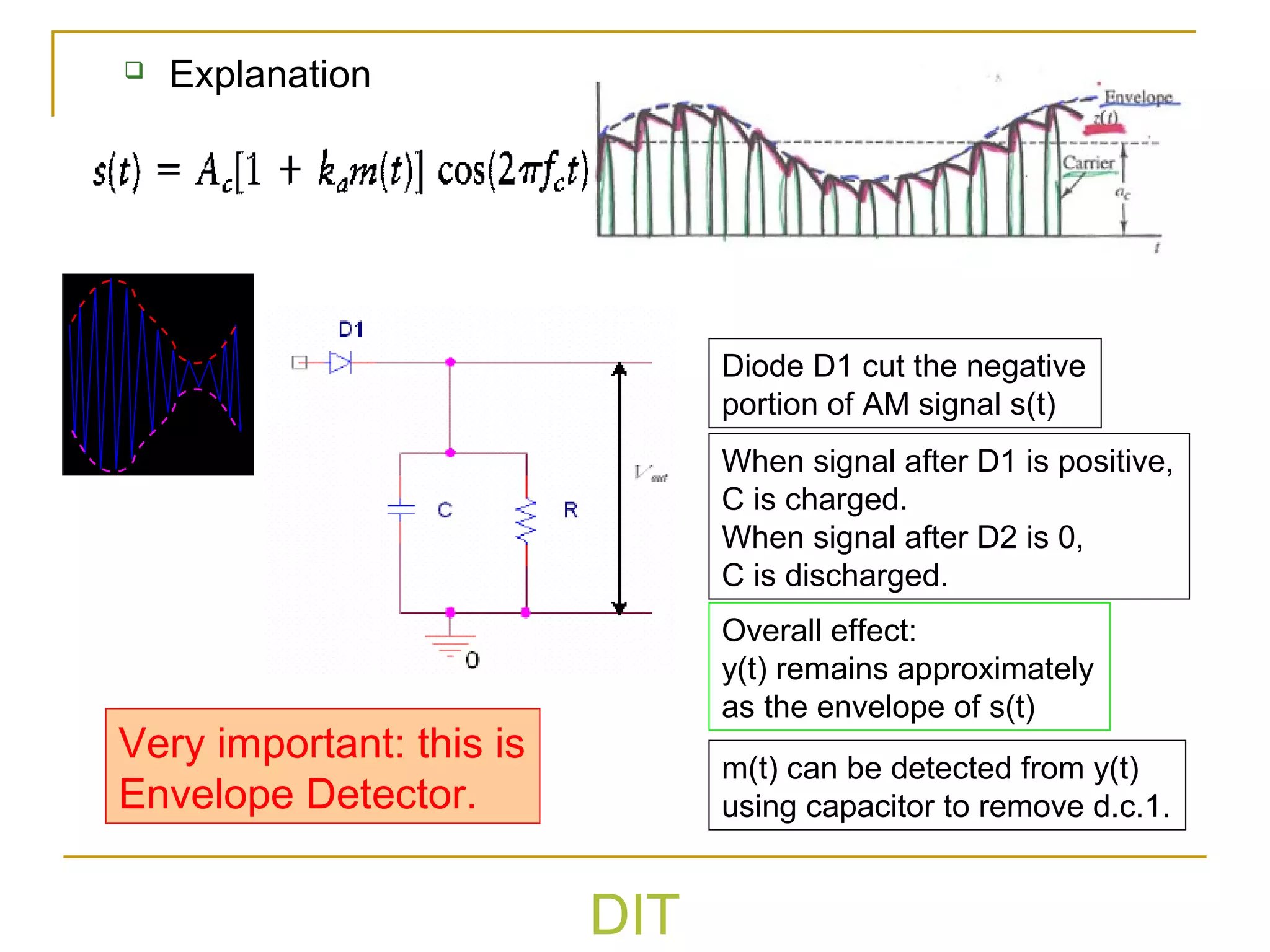
The document discusses various types of analog modulation techniques. It begins by defining analog modulation and describing the key components - the message signal, carrier signal, and modulated signal. It then covers amplitude modulation techniques like AM, DSB-SC, and SSB which vary the amplitude of the carrier signal. Key aspects like bandwidth, power distribution, and detection methods are explained for each technique. The document also touches on angle modulation like FM and discusses metrics for evaluating different modulation schemes.

1. DIT
Dar es Salaam institute of Technology (DIT)
ETU 07123
Introduction to Communication System
Ally, J
jumannea@gmail.com

2. DIT
Analogue Modulation

3. DIT
Introduction to Modulation
 Definitions
 Analog modulation
 Both the message signal and the transmitted signal are
analog signals
 Two classes: amplitude modulation, angle modulation
 Three signals:
 Message signal: the information signal to be modulated and
transmitted
 Carrier signal c(t) : high frequency sinusoidal signal
 Modulated signal: the signal to be transmitted, or the signal
obtained after modulation

4. DIT
Modulation
 It is the process of facilitating the transfer of
information over a medium.
 This is done by changing one or more the
parameters of a signal including power,
frequency, phase and amplitude depending
on the requirement of the transmission
system.

5. DIT
 Baseband, Passband
 Baseband: refers to the signals and systems before
modulation, which have frequencies/bandwidth much lower
than the carrier frequency
 Passband: refers to the signals and systems after (including)
modulation, which have frequencies/bandwidth around the
carrier frequency
 Baseband signal: is usually the message signal
 Passband signal: is usually the modulated signal, or
transmitted signal
Baseband and Passband signals

6. DIT
Baseband and Bandpass Signals
• Baseband signal is the original signal having the original
frequencies when delivered by transmitters.
• In Baseband communication, signals are transmitted
without modulation.
• Bandpass signal is a signal which is modulated by one of
the modulation schemes.
• Demodulation is the process of extracting the baseband
message from the carrier so that it may be processed
and interpreted by the intended receiver

7. DIT
 Message signal m(t) modifies:
 Amplitude: AM  linear modulation
 Phase: PM
 Frequency: FM
 Example Compare signal waveforms
( )A t
( ) ( )f t d t dtφ=
Non-linear modulation)(tφ

8. DIT
Concept of Modulation

9. DIT
Checkpoints for studying each modulation
 Modulated signal (time-domain)
 Spectrum (frequency-domain)
 Parameters: bandwidth, power, etc
 Modulator and demodulator (Principles, block
diagrams or circuits)
 Major properties (advantages/disadvantages
over other modulations)

10. DIT
List of modulation methods we will learn
 Amplitude modulation methods and applications
1. AM (amplitude modulation): AM radio, short wave
radio broadcast,
2. DSBSC (double sideband suppressed carrier AM):
data modem, Color TV’s color signals
3. SSB (single sideband AM): telephone
4. VSB (vestigial sideband AM): TV picture signal
 Angle modulation methods and applications
1. FM (frequency modulation): FM radio broadcast, TV
sound signal, analog cellular phone
2. PM (phase modulation): not widely used, except in
digital communication systems (but that is different)

11. DIT
Amplitude Modulation (AM)
 AM (conventional amplitude modulation)
Amplitude Modulation (AM) is the one which the amplitude of a
sinusoidal carrier is varied in accordance with an incoming
message signal
 Modulated signal
 Carrier:
 Message signal: m(t)
 AM modulated signal
where ka, is a constant called the amplitude
sensitivity of the modulator responsible for
the generation of the modulated signal s(t).

12. DIT
Time-Domain description
The standard form of an AM wave is defined by
 The amplitude of the time function multiplying is called the
envelope of AM wave s(t).
 The envelope of s(t) has essentially the same shape as the baseband signal
m(t) provided that two requirements are satisfied:
1. The amplitude of is always less than unity, that is,
for all t
2. The carrier frequency fc, is much greater than the highest frequency
component W (message bandwidth) of the message signal m(t), that is
(a) Baseband signal m(t) (b) AM wave for (c) AM wave for
( )tfcπ2cos

13. DIT
Frequency-Domain description
The Fourier transform of the AM wave s(t) is given by
(a) Spectrum of baseband signal
(b) Spectrum of AM wave

14. DIT
Generation of AM Waves
 Multipliers difficult to build in hardware
 AM waves typically generated using a nonlinear device to obtain the
desired multiplication
 Square law modulator sums carrier c(t) and information m(t) signals,
then squares them using a nonlinear device. Unwanted terms are
filtered out with a bandpass filter.
 Switched modulation sums c(t) and m(t) then passes sum through a
switch, which approximately multiplies it by a periodic square wave.
This generates the desired signal plus extra terms that are filtered
out.
m(t)
+
Accos(2πfct+φ)
Square
or Switch BPF
s(t)

15. DIT
Modulation Index
The degree of modulation is an important parameter and is known as
the modulation index. It is the ratio of the peak amplitude of the
modulating signal, Am to the peak amplitude of the carrier signal, Ac
(a) Under Modulation (ka < 1)
(b) Ideal Modulation (ka = 1)
(c) Over Modulation (ka > 1)
c
m
a
A
A
k =

16. DIT
Over Modulation
http://www.williamson-labs.com/480_am.htm

17. DIT
Detection of AM waves
 There are two devices for the detection of AM waves, namely, the
square-law detector and the envelope detector
 Square law detector, squares signal and then passes it through a
LPF
 Residual distortion proportional to m2
(t)
 Non-coherent (carrier phase not needed in RX)
 Envelope detection simple alternative method

18. DIT
 Explanation
Diode D1 cut the negative
portion of AM signal s(t)
When signal after D1 is positive,
C is charged.
When signal after D2 is 0,
C is discharged.
Overall effect:
y(t) remains approximately
as the envelope of s(t)
m(t) can be detected from y(t)
using capacitor to remove d.c.1.
Very important: this is
Envelope Detector.

19. DIT
 Bandwidth of AM signal BT = 2W
 AM signal’s bandwidth is twice message bandwidth
 This is also transmitted signal bandwidth, or required
minimum channel bandwidth Bc
 Negative frequency contents of m(t) becomes visible in
positive frequency
 Upper sideband (USB):
 Lower sideband (LSB):
 Transmission power: PT = PM+ Pcarrier
= PUSB + PLSB + Pcarrier
Wfff cc +≤≤
cc ffWf ≤≤−

20. DIT
AM Power Distribution
 In any electrical circuit, the power dissipated is
equal to the voltage squared divided by the
resistance.
 Mathematically, power in an unmodulated carrier:
 The upper and lower sideband powers is given by:
 The total power in AM wave is equal to:
R
A
P c
c
2
2
=
( )
482
2/ 2222
ccc
lsbusb
P
R
A
R
A
PP
µµµ
====






+=+=++=++=
2
1
244
2222
µµµµ
c
c
c
cc
clsbusbct P
P
P
PP
PPPPP

21. DIT
AM – Modulation Efficiency
Definition : The modulation efficiency is the percentage of the total power of
the modulated signal that conveys information.
Only “Sideband Components” – Convey information
Modulation Efficiency:
Voltage Spectrum of the AM signal:
Translated version of
message signal
Carrier line spectral
component

22. DIT
Major Properties of AM
 Advantages
 Simplicity in implementation, especially in receiver and
transmitter
 The major reason that AM was the first & most popular
broadcasting methods during early days
 Disadvantages
 Waste power and bandwidth
 Carrier components wastes a major portion power, but
carrier does not have message information
 Both USB and LSB are transmitted, which carry the same
message information

23. DIT
Ways for AM improvement
 To enhance power efficiency
 Reduce/remove carrier: DSB-SC
 Remove one/partial sideband: SSB, VSB
 To enhance bandwidth efficiency
 Remove one/partial sideband: SSB, VSB
 Multiplex two message signals together: QAM
 Cost for the improvement
 More expensive implementation
 The simple envelope detector is no longer applicable

24. DIT
Double-Sideband Suppressed-carrier (DSB-SC)
 In the standard form of Amplitude Modulation (AM), the carrier wave
c(t) is completely independent of the message signal m(t), which
means that the transmission of the carrier wave represents a waste
of power.
 To overcome this shortcoming , we may suppress the carrier
component from the modulated wave, resulting in double-sideband
suppressed carrier (DSB-SC) modulation.
 Thus, by suppressing the carrier, we obtain a modulated wave that
is proportional to the product of the carrier wave and the message
signal.

25. DIT
Time-Domain Description
 The standard form of a DSB-SC wave is defined by
 This modulated wave undergoes a phase reversal whenever the
message signal m(t) crosses zero, as illustrated in figure below
(a) Baseband signal (b) DSB-SC modulated wave
( ) ( ) ( )tmtcts =
( ) ( ) ( )tmtfAts cc π2cos=

26. DIT
The Fourier transform of the DSB-SC wave s(t) is given by
(a) Spectrum of message signal
(b) Spectrum of DSB-SC modulated wave
Frequency-Domain Description

27. DIT
Generation of DSB-SC Waves
 A DSB-SC modulated wave consists simply of the product of the
message signal and the carrier wave. A device achieving this
requirement is called a Product Modulator.
 Remove inefficient constant term
 Modulated signal is
 Can also use ring modulator: diodes and inductors

28. DIT
Coherent Detection of DSB-SC Modulated Wave
 The baseband signal m(t) can be uniquely recovered from a DSB-
SC wave s(t) by first multiplying s(t) with a locally generated
sinusoidal wave and then low-pass filtering the product
 It is assumed that the local oscillator output is exactly coherent or
synchronized, in both frequency and phase, with the carrier wave
c(t) used in the product modulator to generate s(t).
 This method of demodulation is known as coherent detection or
synchronous detection.

29. DIT
Coherent Detection of DSB-SC Modulated Wave-2
 We find that the product modulator output is:
 The first term represents a DSB-SC modulated signal with a carrier
frequency 2fc, whereas the second term is proportional to the
baseband signal m(t).
 the first term is removed by the low-pass filter, this requirement is
satisfied by choosing fc > W. At the filter output we then obtain a
signal given by
 The demodulated signal is therefore proportional to m(t) when the
phase error is a constant.

30. DIT
Coherent Detection of DSB-SC Modulated Wave-3
 The amplitude of this demodulated signal is maximum when
and it is minimum (zero) when
 As long as the phase error is constant, the detector provides an
undistorted version of the original baseband signal m(t).
 In practice, however, we usually find that the phase error varies randomly
with time, due to random variations in the communication channel. The
result is that at the detector output, the multiplying factor also varies
randomly with time, which is obviously undesirable.
 Therefore, provision must be made in the system to maintain the local
oscillator in the receiver in perfect synchronism, in both frequency and
phase, with the carrier wave used to generate the DSB-SC modulated signal
in the transmitter.
 The resulting system complexity is the price that must be paid for
suppressing the carrier wave to save transmitter power.
φcos

31. DIT
Costas Loop (DSB-SC Demodulator)
Goal: Maintain οφ ≈∆

32. DIT
Costas Loop
 One method of obtaining a practical synchronous receiver system, suitable
for demodulating DSB-SC waves, is to use the Costas loop.
 This receiver consists of two coherent detectors supplied with the same
input signal, namely, the incoming DSB-SC wave Accos(2πfct)m(t), but with
individual local oscillator signals that are in phase quadrature with respect to
each other.
 The frequency of the local oscillator is adjusted to be the same as the
carrier frequency fc, which is assumed known a priori.
 The detector in the upper path is referred to as the in-phase coherent
detector or I-channel, and that in the lower path is referred to as the
quadrature-phase coherent detector or Q-channel.
 These two detectors are coupled together to form a negative feedback
system designed in such a way as to maintain the local oscillator
synchronous with the carrier wave.

33. DIT
Double Side Band Suppressed Carrier
Power in a AM signal is given by
( ) ( )
2
1
2
1 2222
tmAAts cc +=
Discrete carrier power Sideband power
Discrete carrier power can be eliminated (Suppressing carrier )if m(t) is
assumed to have a zero DC level
Then ttmAts cc ωcos)()( =
Spectrum 
( ) ( )[ ]cc
c
ffMffM
A
fS ++−=
2
)(
Since no power is wasted in carrier the efficiency is
Power 
( ) ( )
2
1 222
tmAts c=
( )
( )
%1001002
2
=×=
tm
tm
E

34. DIT
Noise in AM Receivers
 Power in s(t) is 0.5Ac
2
Pm
 Power in n(t) is N0B
SNR=Pm/Pn= Ac
2
Pm/(2N0B)= Ps/(N0B) (SNR at the receiver input)
 Power in m′(t) is 0.25Ac
2
Pm (half the power in s(t))
 Power in n′(t) is 0.5N0B (PSD 0.25N0 over BW 2B)
SNR=Pm´/Pn´= Ac
2
Pm/(2N0B)= Ps/(N0B) (SNR at the receiver output)
Product
Modulato
r
m´(t)+ n´(t)
Accos(2πfct+φ)
s(t)=Accos(2πfct+φ)m(t
) +
n(t)
LPF
1
White Gaussian noise
(AWGN)
-B B

35. DIT
Single-SideBand (SSB) Modulation
 Standard AM and DSB-SC Modulation are wasteful of
bandwidth because they both require a transmission
bandwidth equal to twice message the message
bandwidth.
 This means that insofar as the transmission of
information is concerned, only one sideband is
necessary, and no information is lost.
 Thus the channel needs to provide only the same
bandwidth as the message signal, a conclusion that is
intuitively satisfying.
 When only one sideband is transmitted, the modulation
is referred to as single-sideband modulation

36. DIT
Single Sideband Modulation(2)
 Only transmits upper or lower sideband of AM and DSBSC
 The transmitted signal can be written in terms m(t) and the
Hilbert Transform of m(t)
 Use same demodulator as DSBSC
 SSB has half the SNR of DSBSC for half the transmit
power: no SNR gain
 SSB can introduce significant distortion at DC where the
sidebands meet: not good for TV signals
USB
LSBM(f)
0 fc-fcB-B
USB
LSB
)]2sin()()2cos()([
2
)( φπφπ +±+= tftmtftm
A
ts chc
c

37. DIT
Baseband Representation of Modulated
Signals
 Baseband signal representation is a compact way to represent
passband signals.
 All passband signals at carrier frequency fc can be written as s(t) = sI(t)
cos(2fct) + sQ(t) sin(2fct).
 sI(t) is called the in-phase signal component; sQ(t) is called the
quadrature signal component.
 The sine and cosine are orthogonal signals, can be used to separate
out the in-phase and quadrature components from s(t).
 We define as the baseband signal representation.
Then which is a compact way to represent and
analyze passband signals.

38. DIT
Generating of SSB modulated wave by phase
discrimination method
 The phase discrimination method of generating an SSB modulated
wave involves two separate simultaneous modulation processes and
subsequent combination of the resulting modulation products.
 The system uses two product modulators, I and Q, supplied with
carrier waves in phase quadrature to each other.
 The incoming baseband signal m(t) is applied to product modulator I,
producing a modulated DSBSC wave that contains reference phase
sidebands symmetrically spaced about carrier frequency fc.
 The hilbert transform mh(t) of m(t) is applied to product modulator Q,
producing DSBSC modulated wave that containssideband having
identical amplitude spectra to those of modulator I, but with phase
spectra such that vector addition or subtraction of the two modulator
outputs results in cancellation of one setof sidebands and
reinforcement of the other set.
 The use of plus sign yields SSB wave with only the upper sideband,
whereas the use of minus sign yields SSB wave with only upper
sideband.

39. DIT
Block diagram for generating of SSB modulated
wave by phase discrimination method

40. DIT
Demodulation of SSB wave
 To recover the baseband signal m(t) from the SSB wave s(t), we
have to shift the spectrum by the amounts so as to convert
the transmitted sideband back into the baseband signal.
 This can be accomplished using coherent detection, which
involves applying the SSB wave s(t), together with locally
generated carrier , assumed to be of unit amplitude for
convenience, to a product modulator and then low-pass filtering
the modulator output.
cf+
−
( )tfcπ2cos
,

41. DIT
Demodulation of SSB wave (2)
 The product modulator output is given by
 The first term is the desired message signal. The second term
represents an unwanted components in the product modulator
output that is removed by low-pass filtering.
 The detection of SSB modulated waves assume perfect
synchronization between the local carrier and that in the transmitter
both in frequency and phase. The effect of a phase error Ф in the
locally generated carrier wave is to modify the detector output as
follows
( ) ( ) ( )tstftv cπ2cos=
( ) ( ) ( ) ( ) ( )[ ]
( ) ( ) ( ) ( ) ( )[ ]tftmtftmAtmA
tftmtftmtfA
cccc
cccc
ππ
πππ
4sin~4cos
4
1
4
1
2sin~2cos2cos
2
1
+=
±=
( ) ( ) ( ) φφ sin~
4
1
cos
4
1
tmAtmAtv cco =

42. DIT
Demodulation of SSB wave (3)
 Owing to the phase error Ф, the detector output
vo(t) contains not only the message signal m(t)
but also its Hilbert transform mh(t).
 Consequently, the detector output suffers from
phase distortion. This phase distortion is usually
not serious with voice communications because
the human ear is relatively insensitive to phase
distortion.
 In the transmission of music and video signals,
on the other hand, phase distortion in the form of
a constant phase difference in all components
can be intolerable.

43. DIT
Vestigial Side-Band (VSB) Modulation
 Single-sideband modulation is well-suited for the
transmission of voice because of the energy gap that exists
in the spectrum of voice signals between zero and a few
hundred hertz.
 When the message signal contains significant components
at extremely low frequencies i.e. television signals, the
upper and lower sidebands meet at the carrier frequency.
This means SSB modulation is inappropriate for the
transmission of television signals.
 This difficulty suggests another scheme known as vestigial
sideband modulation (VSB), which is a compromise
between SSB and DSBSC modulation.

44. DIT
Vestigial Sideband
 VSB is similar to SSB but it retains a small portion (a vestige) of the
undesired sideband to reduce DC distortion. Transmits USB or LSB
and vestige of other sideband
 Reduces bandwidth by roughly a factor of 2
 VSB signals are generated using standard AM or DSBSC modulation,
then passing modulated signal through a band-pass filter i.e. it is the
special design of the band-pass filter that distinguishes VSB
modulation from SSB modulation.
 Demodulation uses either standard AM or DSBSC demodulation
 VSB used for image transmission in TV signals
USB

45. DIT
Generation of VSB modulated wave
 The transmission bandwidth of VSB modulation is given by
where W is the message bandwidth, and f, is the width of the vestigial
sideband
 To generate a VSB modulated wave, we pass a DSBSC modulated
wave through a sideband shaping filter.
 The exact design of this filter depends on the desired spectrum of the
VSB modulated wave.
 the VSB modulated wave is described in the time domain as
 This is the desired representation representation for a VSB modulated
wave containing a vestige of the lower sideband. The component
0.5Acm(t) constitutes the in-phase component of this VSB modulated
wave, and 0.5AcmQ(t) constitutes the quadrature components.
( ) ( ) ( ) ( ) ( )tftm
A
tftm
A
ts cQ
c
c
c
ππ 2sin
2
2cos
2
−=

46. DIT
Scheme for generation and demodulation
of a VSB modulated wave
 Block diagram of VSB modulator
 Block diagram of VSB demodulator

47. DIT
Envelope detection of a VSB wave plus
carrier
 In commercial television broadcasting, a sizable carrier
is transmitted together with the modulated wave.
 This makes it possible to demodulate the incoming
modulated wave by an envelope detector in the receiver.
 In commercial television broadcasting, the vestigial
sideband occupies a width of about 1.25 MHz, or about
one-quarter of a full sideband.
 This has been determined empirically as the width of
vestigial sideband required to keep the distortion due to
mQ(t) within tolerable limits when when the percentage
modulation is nearly 100.