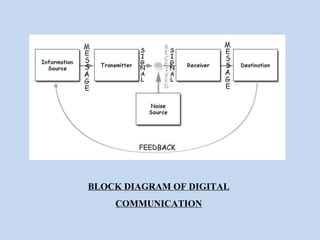
Channel capacity is the maximum rate at which information can be reliably transmitted over a communication channel, constrained by factors like bandwidth and noise power. The document explains key concepts such as bit rate, bandwidth, and digital communication, along with Shannon's mathematical framework for determining channel capacity. It concludes that Shannon's theory applies broadly across various fields beyond telecommunications, underscoring its significance in information theory.

1. CHANNEL CAPACITY
NAME- PALLAB DAS

2. INTODUCTION
• Channel capacity, in Electrical engineering, Computer
science, and Information theory, is the tight upper
bound on the rate at which information can be reliably
transmitted over a communication channel .
• The channel capacity of a given channel is the highest
information rate (in units of information per unit time) that
can be achieved with arbitrarily small error probability.
• Bandwidth and noise power place a restriction upon the
rate of information through a channel for low error
transmission. The highest bit rate achievable for no
error transmission is termed as the channel capacity.

3. COMMUNICATION -
• According to Merriam Webster process by which
information is exchanged between individuals
through a common system of symbols, signs, or
behavior.
• DIGITAL COMMUNICATION –
Digital communications is any exchange of data
that transmits the data in a digital form. For
example, communications done over
the Internet is a form of digital communication.

4. • According to Cambridge dictionary
to direct something into a particular place
or situation is called a channel. Following are list of
some of the forms of communication with channels
of disseminating information. This are,
• i) Oral
• ii) Documentary
• iii) Audio - Visual

5. BIT RATE -
• Bit rate, as the name implies, describes the rate at which bits are
transferred from one location to another. In other words, it measures how
much data is transmitted in a given amount of time. Bit rate is commonly
measured in bits per second (bps), kilobits per second (Kbps), or megabits
per second (Mbps).
BANDWIDTH –
Bandwidth describes the maximum data transfer rate of
a network or Internet connection. It measures how much data can
be sent over a specific connection in a given amount of time. For
example, a gigabit Ethernet connection has a bandwidth of
1,000 Mbps. An Internet connection via cable modem may provide
25 Mbps of bandwidth.

6. BLOCK DIAGRAM OF DIGITAL
COMMUNICATION

7. The components of the information model of C.E .
Shannon is explained here :
•Information Source: An ensemble of messages from
which selections are made for transmission.
•Encoder : Encodes a message to a signal There will be
one to one correspondence between the message alphabet
and the signal, therefore, there will be no ambiguity in
the encoding process
•Channel : Band of frequencies within which signals must be
kept
•Decoder : Decodes a message from a signal.
•Noise : Received signal is not the one transmitted.

8. Mathematical Explanation of channel capacity:
If a source gives M equally likely message M >>1, With rate
of information R and given channel with capacity C.
Then if
R <=C In this condition error free transmission is possible
in presence of noise
If
R > c In this conditions probability of error is close to
unity or equal to 1.

9. Shannon Hartley channel capacity formula :
Here
• C - Channel capacity in bits per sec
• B - Bandwidth of the channel in hertz
• S - Average signal power over the bandwidth (watt)
• N - Average power of the noise and interference over the
bandwidth (watts)
• S/N – Signal to Noise Ratio (SNR) or carrier – to – noise
ratio (CNR)
• Here one can receive a signal with noise in every session.
Because of noise is there at the channel we receive signal
and noise both together.

10. Noiseless Channels and Nyquist
Theorem
• For a noiseless channel, Nyquist theorem gives the relationship
• between the channel bandwidth and maximum data rate that can be
transmitted over this channel.
Nyquist Theorem
mBC 2log2
C: channel capacity (bps)
B: RF bandwidth
m: number of finite states in a symbol of transmitted signal

11. So we receive
Signal = Signal power (S) + Noise Power (N)
And its mean square value is
Where S = signal power
N = Noise power and
Root ( ) means square value of signal is ,
So noise power is N and its mean square value is .
So if we want to identify number of levels will be separated
without error is
m = Ratio of Signal / Noise signal
m =

12. m - Here levels of signals without error ,
is denoted as received signal with error and is noise signal.
So here the signal without error is
>
So digital information is -
I = log2 m
= log 2
= ½ log2
Here I is digital information
m is the signal without error and it is
So the channel signal is ½ log 2

13. Now if a channel transmits K pulses per second
then channel capacity is
C = IK (Information multiplied with pulses)
= K/2 log2 ( 1+S/N)
• From Nyquist theorem we know that k=2B, then we
get the value of channel capacity C,

14. Conclusion -
 Here we can see that the channel capacity is
measured with the multiplication of pulses
per second and information. This is how we
can measure the channel capacity.
 Though Shannon’s theory was presented
with regard to the problem of transmitting
error- free messages across telephone lines,
this theory is being used in such fields as ,
psychology, education , managmen decision
process and information science. Because of its
generality, this theory became known as
information theory.

15. THANK YOU