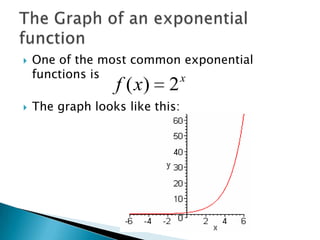
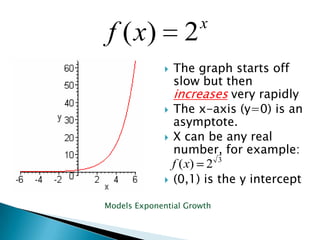
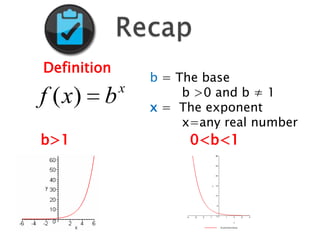
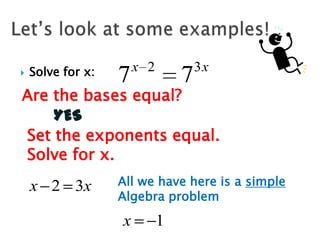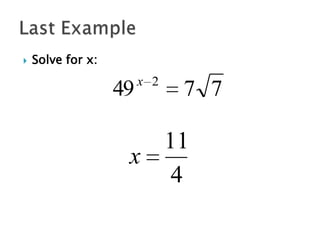The document discusses exponential functions and exponential equations. Exponential functions have the form f(x) = bx, where b is the base and x is the exponent. These functions are important in modeling real-world phenomena like population growth. Exponential equations set the exponents of the same base equal to solve for the variable. They can be solved by rewriting all terms to have the same base, setting the exponents equal, and solving the resulting equation.

2. The exponential function is very important
in math because it is used to model many
real life situations.

◦ For example: population growth and
decay, compound interest, economics,
and much more.

3. f ( x) b
x
Question…
How is this function
different from functions that
we have worked with
previously?

4. Answer:
The exponent is the variable!
f ( x) b
x
Question…
b = The base
b >0 and b ≠ 1
x = The exponent
x=any real number
Is f(x)=x3 an exponential
function?
NO

5. 
One of the most common exponential
functions is
x
f ( x)

2
The graph looks like this:

6. f ( x)
2
x
The graph starts off
slow but then
increases very rapidly
 The x-axis (y=0) is an
asymptote.
 X can be any real
number, for example:
f (x) 2 3
 (0,1) is the y intercept

Models Exponential Growth

7. Question…
What would a graph look like if b is
between 0 and 1?
For example:
x
f ( x)
1
2

8. f ( x)
1
2
x



The graph starts off
very high but then
decreases very rapidly
The x-axis (y=0) is an
asymptote.
X can be any real
number, for example:
f (x)

1
2
(0,1) is the y intercept
Models Exponential Decay

9. Definition
f ( x) b
b>1
x
b = The base
b >0 and b ≠ 1
x = The exponent
x=any real number
0<b<1

11. 
What is an exponential equation?
◦ An equation where the variable is the
exponent.
◦ Example:
2
x
1
8

12. 2
1
8
x
Any ideas?
What if we changed
the right side to
2
x
2
3
2
3
Now What?

13. x
2
◦If 2
◦Then x=?
◦Check:
-3= 1
◦2
8
3
3
Then we have solved
2
x
1
8

14. 1.Express each side of the equation as a
power of the same base.
2.Set the exponents equal and solve.
3.Check your answer
Main
idea
If the bases are
the same, set the
exponents equal!

15. 
Solve for x:
7
x 2
7
3x
Are the bases equal?
YES
Set the exponents equal.
Solve for x.
x 2 3x
All we have here is a simple
Algebra problem
x
1

16. x = -1
7
7
x 2
( 1) 2
7
3
3x
7
3( 1)
7
3
7
It checks!

17. 
Solve for x:
5
4 t
t 1
25
Are the bases equal?
NO
Change the right side to:
Simplify:
Solve!
5
4 t
t
5
2
2t 2
2 t 1
(5 )

18. t=2
4 t
t 1
5
25
4 2
2 1
5
25
2
1
5 25
It checks!

19. 
Solve for x:
49
x 2
7 7
11
x
4

20. 
Solve for x:
49
x 2
7 7
Are the bases equal?
NO
2 x
Change both sides to: (7 )
Simplify:
Solve!
7
2x 4
2
7*7
3
2
7
3
2x 4
2
11
x
4
1
2

21. x = 11/4
x 2
49 11
49 4
2
3
4
3
2 4
73 7
7 23
2
3
2
49
7
(7 )
7
It checks!

22. REVIEW
1. Exponential function:
f ( x) b
Key Point:
2. Exponential Equations:
Example:
Rewrite as:
x
The exponent is
the variable
b= the base
b >0 and b ≠1
X= the exponent
X = any real number
An equation where the
exponent is the variable
4x 6
2
16
4x 6
4
2How to solve:
2
Set exponents
4x 6 4
If the bases are the
equal:
Check:
same, set the10
exponents
x
Solve:
equal!
4
2
4(
10
) 6
4
10 6
2
2
4
16
16
16
It checks!

23. Homework:
Exponential
Equations
Worksheet