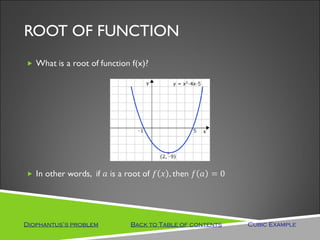
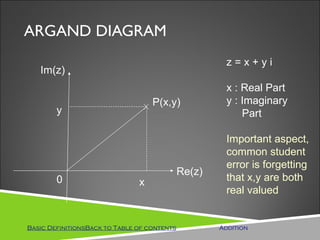
This document discusses approaches to teaching complex numbers. It describes an axiomatic approach, utilitarian approach, and historical approach. The historical approach builds on prior knowledge of quadratic equations and introduces complex numbers to solve problems like finding the roots of quadratic and cubic equations. The document also covers definitions of complex numbers, addition, subtraction, multiplication, and division of complex numbers. It discusses pedagogical considerations like using multiple representations and building on students' prior knowledge.

1. COMPLEX NUMBERS
Beertino
John
Yeong Hui
Yu Jie

2. CONTENTS
Beertino Yeong Hui
 Approaches/pedagogy  A level syllabus
 Diophantus’s problem  Pedagogical Consideration
 roots of function  Multiplication
 Cubic Example and Division of
complex numbers
 Complex conjugates
Yu Jie
 A level syllabus
 Pedagogical considerations
 Basic definition & John
Argand Diagram  A Level syllabus
 Addition and  Pedagogical considerations
Subtraction of
complex numbers  Learning difficulties
 Uniqueness of Complex Numbers

3. APPROACHES/PEDAGOGY
 Axiomatic Approach
 Common in textbooks.
 Start by defining complex numbers as numbers of the form a+ib where a, b are real
numbers.
Back to Table of contents Diophantus’s problem

4. APPROACHES/PEDAGOGY
 Utilitarian Approach
 Briefly describe Complex Numbers lead to the theory of fractals
 It allows computer programmers to create realistic clouds and mountains in video
games.
Back to Table of contents Diophantus’s problem

5. APPROACHES/PEDAGOGY
 Totalitarian Approach! ( Just kidding )
Back to Table of contents Diophantus’s problem

6. APPROACHES/PEDAGOGY
 Historical Approach
 Why this approach?
 Real questions faced by mathematicians.
 Build on pre-existing mathematical knowledge,
 Quadratic formula
 Roots.
Back to Table of contents Diophantus’s problem

7. APPROACHES/PEDAGOGY
 So, how does the approach goes?
 First, bring about the quadratic problem.
 Tapping on prior knowledge
 Quadratic formula.
 Roots of an equation.
 Followed with definition of root.
 Then sub value into root to get a cognitive conflict.
 Give another example, this time it’s cubic
 Tap on prior knowledge again
 Completing Square to get to Completing Cube (Cardano’s Method)
 Solve to get a weird answer.
 Show that weird answer is 4, and get another cognitive conflict.
Back to Table of contents Diophantus’s problem

8. DIOPHANTUS’S PROBLEM
 Diophantus' Arithhmetica (C.E 275) A right-angled triangle has area 7
square units and perimeter 12 units. Find the lengths of its sides.
Approaches/Pedagogy Back to Table of contents Root of Function

9. SOLUTION AND PROBLEM
Approaches/Pedagogy Back to Table of contents Root of Function

10. ROOT OF FUNCTION
Diophantus’s problem Back to Table of contents Cubic Example

11. ROOT OF FUNCTION
Diophantus’s problem Back to Table of contents Cubic Example

12. CUBIC EXAMPLE
Root of Function Back to Table of contents

13. CUBIC EXAMPLE
Root of Function Back to Table of contents

14. LASTLY
Root of Function Back to Table of contents

15. A-LEVEL SYLLABUS
Back to Table of contents Pedagogical considerations

16. PEDAGOGICAL CONSIDERATIONS
 Operations in complex plane is
similar but not exactly the same
as vector geometry (see complex
multiplication and division)
 Building on Prior Knowledge
 Rules-Based Approach vs
Theoretical Understanding
SyllabusBack to table of contents (Teaching) Basic Definition

17. PEDAGOGICAL CONSIDERATIONS
 Multimodal Representation and usage of similarity in
vector geometry for teaching of complex addition and
subtraction
 Algebraic proof for uniqueness of complex numbers
and should it be taught specifically
 No ordering in complex plane, not appropriate to talk
about
z1 > z2
 ordering is appropriate for modulus, since modulus of
complex numbers are real values
SyllabusBack to table of contents (Teaching) Basic Definition

18. BASIC DEFINITONS
First defined by Leonard Euler, a swiss
mathematician, a complex number, denoted
by i, to be i2 = -1
In general, a complex number z can be
written as
where x denotes the real part and y denotes
the imaginary part
Pedagogical considerationsBack to Table of contents Argand Diagram

19. ARGAND DIAGRAM
z=x+yi
Im(z)
x : Real Part
P(x,y) y : Imaginary
y Part
Important aspect,
common student
error is forgetting
Re(z)
0 x that x,y are both
real valued
Basic DefinitionsBack to Table of contents Addition

20. EXTENSION FROM REAL NUMBERS
(ENGAGING PRIOR KNOWLEDGE)
The Real Axis
Im(z)
(x-axis) represents
the real number
z line.
y
|z| In other words the
real numbers just
have the imaginary
θ part to be zero.
Re(z)
0 x
e.g. 1 = 1 + 0 i
Basic DefinitionsBack to Table of contents Addition

21. ADDITION OF COMPLEX NUMBERS
 Complex Addition
 Addition of 2 complex numbers
 z1 = x1 + y1i, z2 = x2 + y2i
 z1 + z2 = (x1 + y1i) + (x2 + y2i)
= (x1 + x2) + (y1 + y2) i
 Addition of real and imaginary portions and summing the 2
parts up
 Geometric Interpretation (vector addition)
Rationale
Multimodal Representation: Argand Diagram
Engaging prior knowledge: Addition for Real Numbers
Argand DiagramBack to Table of contents Subtraction

22. MMR IN ADDITION
 Multimodal Representation used: Pictorial
 Geometric Interpretation
 Vector Addition
Im(z)
z1 z1+z2
z2
Re(z)
0
Argand DiagramBack to Table of contents Subtraction

23. SUBTRACTION OF COMPLEX NUMBERS
 Complex Subtraction
 Difference of 2 complex numbers
 z1 = x1 + y1i, z2 = x2 + y2i
 z1 - z2 = (x1 + y1i) - (x2 + y2i)
= (x1 - x2) + (y1 - y2) i
 Subtraction of real and imaginary portions and summing the 2
parts up
 Geometric Interpretation (vector subtraction)
Rationale
Multimodal Representation: Argand Diagram
Engaging prior knowledge: Subtraction for Real Numbers
AdditionBack to Table of contents Uniqueness

24. MMR IN SUBTRACTION
 Multimodal Representation used: Pictorial
 Geometric Interpretation
 Vector Subtraction
Im(z)
z1-z2 z1
Re(z)
-z2 0
AdditionBack to Table of contents Uniqueness

25. UNIQUENESS OF COMPLEX NUMBERS
 If two complex numbers are the same, i.e. z1 = z2, then their real parts
must be equal, and their imaginary parts are equal.
 Algebraically, let z1 = x1 + y1i, z2 = x2 + y2 i, if z1 = z2 then we have
 x1 = x2 and y1 = y2
 Geometrically, from the argand diagram we can see that if two complex
numbers are the same, then they are represented by the same point on
the argand diagram, and immediately we can see that the x and y co-
ordinates of the point must be the same.
Subtraction Back to table of contents

26. A-LEVEL SYLLABUS
Back to Table of contents Pedagogical Considerations

27. PEDAGOGICAL CONSIDERATIONS
 Operations in complex plane is similar but not exactly the same as
vector geometry (see complex multiplication and division)
 Limitations in relating to Argand diagram (pictorial) for teaching of
complex multiplication and division in Cartesian form
 Building on Prior Knowledge
 Rules-Based Approach vs Theoretical Understanding
Syllabus Back to table of contents Multiplication

28. PEDAGOGICAL CONSIDERATIONS
 Properties…
 of complex multiplication assumed
(commutative, associative, distributive over complex addition)
 of complex division assumed
(not associative, not commutative)
 of complex conjugates
(self-verification exercise)
 Notion of identity element, multiplicative inverse
 Use of GC
 Accuracy of answers
Syllabus Back to table of contents Multiplication

29. MULTIPLICATION OF COMPLEX NUMBERS
 Complex multiplication
 Multiplication of 2 complex numbers
 z1 = x1 + y1i, z2 = x2 + y2i
 z1 z2 = (x1 + y1i) (x2 + y2i)
= x1x2 + x1y2i + x2y1i - y1y2i2
= (x1x2 - y1y2 ) + (x1y2+ x2y1)i
 Geometric Interpretation (Modulus Argument form)
Rationale
Engaging prior knowledge: Multiplication for Real Numbers
Pedagogical considerations Back to Table of contents Division

30. MULTIPLICATION OF COMPLEX NUMBERS
 Complex multiplication
 Scalar Multiplication
 z = x + yi, k real number
kz = k(x + yi)
= kx + kyi
 Geometric Interpretation (vector scaling)
 k ≥ 0 and k < 0
Rationale
Multimodal Representation: Argand Diagram
Engaging prior knowledge: Multiplication for Real Numbers
Pedagogical considerations Back to Table of contents Division

31. MULTIPLICATION OF COMPLEX NUMBERS
 i4n = I, i4n+1 = i, i4n+2 = -1, i4n+3 = -I for any integer n
 Explore using GC (Limitations)
 Extension of algebraic identities from real number system
 (z1 + z2 )(z1 – z2 ) = z12 – z22
 (x + iy)(x – iy) = x2 – xyi + xyi + y2 = x2 + y2
 ALWAYS real
Rationale
Engaging prior knowledge: Multiplication for Real Numbers
Cognitive process: Assimilation
Pedagogical considerations Back to Table of contents Division

32. DIVISION OF COMPLEX NUMBERS
 Complex division
 Division of 2 complex numbers (Realising the denominator)
 z1 = x1 + y1i, z2 = x2 + y2i
.
z1 x1 + y1i x1 + y1i ( x2 − y2i ) x1 x2 + y1 y2 x2 y1 − x1 y2
= = = + 2 i
z2 x2 + y2i x2 + y2i ( x2 − y2i ) x2 + y2
2 2
x2 + y2 2
Rationale
Engaging prior knowledge: Rationalising the denominator
Multiplication Back to Table of contents Conjugates

33. DIVISION OF COMPLEX NUMBERS
 Solve simultaneous equations
(using the four complex number operations)
 Finding square root of complex number
Multiplication Back to Table of contents Conjugates

34. COMPLEX CONJUGATES
 Let z = x + iy. The complex conjugate of z is given by z* = x – iy.
 Conjugate pair: z and z*
 Geometrical representation: Reflection about the real axis
 Multiplication: (x + iy)(x – iy) = x2 + y2
 Division: Realising the denominator
Rationale
 Bruner’s CPA
 Recalling prior knowledge, Law of recency
DivisionBack to Table of contents Learning Difficulties

35. COMPLEX CONJUGATES
 Properties:
Exercise for students (direct verification)
 1. Re(z*) = Re(z); Im(z*) = -Im(z) 7. (z1 + z2)* = z1* + z2*
 2. |z*| = |z| 8. (z1z2)* = z1*z2*
 3. (z*)* = z 9. (z1/z2)* = z1*/z2*,
 4. z + z* = 2Re(z); z – z* = 2Im(z) if z2 ≠ 0
 5. zz* = |z|2
 6. z = z* if and only if z is real
Rationale
 Self-directed learning
DivisionBack to Table of contents Learning Difficulties

36. LEARNING DIFFICULTIES
/COMMON MISTAKES
 In z = x + yi, x and y are always REAL numbers
 Solve equations using z directly or sub z = x + yi
 Common mistake: (1 + zi)* = (1 – zi)
 Confused with (x + yi)* = (x - yi)
DivisionBack to Table of contents

37. A-LEVEL SYLLABUS
Back to Table of contents Pedagogical Considerations

38. PEDAGOGICAL CONSIDERATION
 Start with a simple quadratic equation
 Example: x2 + 2x + 2 = 0.
 Get students to observe and comment on the roots.
Rationale:
 Bruner’s CPA Approach: Concrete
 Engaging Prior Knowledge
SyllabusBack to Table of contents Learning Difficulties

39. PEDAGOGICAL CONSIDERATION
 Direct attention to discriminant of quadratic equation
 What can we say about the discriminant?
Rationale:
 Engaging Prior Knowledge:
 Linking to O-Level Additional Maths knowledge
 Involving students in active learning (Vygotsky’s ZPD)
SyllabusBack to Table of contents Learning Difficulties

40. PEDAGOGICAL CONSIDERATION
 Examples on Solving for Complex Roots of Quadratic
Equations
 Expose students to different methods:
 Quadratic Formula
 Completing the Square Method
Rationale:
Making Connections between real case and complex case
Getting students to think actively
SyllabusBack to Table of contents Learning Difficulties

41. PEDAGOGICAL CONSIDERATION
 Different version: What if we are given one complex root?
Example:
If one of the roots α of the equation z2 + pz + q = 0 is 3 − 2i,
and p, q ∈ ℝ , find p and q.
Rationale:
Understanding and applying concepts learnt
SyllabusBack to Table of contents Learning Difficulties

42. PEDAGOGICAL CONSIDERATION
Good to
 Fundamental Theorem of Algebra
know
Over the set of complex numbers, every polynomial with real
coefficients can be factored into a product of linear factors.
Consequently, every polynomial of degree n with real coefficients
has n roots, subjected to repeated roots.
Rationale:
Making Connections to Prior Knowledge in Real Case
SyllabusBack to Table of contents Learning Difficulties

43. PEDAGOGICAL CONSIDERATION
Good to
 Visualizing Complex Roots
know
 Exploration with GeoGebra
Rationale:
Stretch higher ability students to think further
Motivates interest in topic of complex numbers
SyllabusBack to Table of contents Learning Difficulties

44. PEDAGOGICAL CONSIDERATION
 Extending from quadratic equations to cubic equations
 Can we generalize to any polynomial?
 Recall: finding conjugate roots of polynomials with real
coefficients
Rationale:
Making sense through comparing and contrasting
SyllabusBack to Table of contents Learning Difficulties

45. LEARNING DIFFICULTIES
/COMMON MISTAKES
 X: complex roots will always appear in conjugate pairs
 ‘No roots’ versus ‘No real roots’
 Difficulty in applying factor theorem
 Careless when performing long division
 Application of ‘uniqueness of complex numbers’ does
not occur naturally
Pedagogical ConsiderationsBack to Table of contents