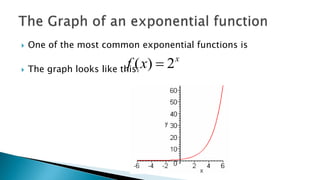
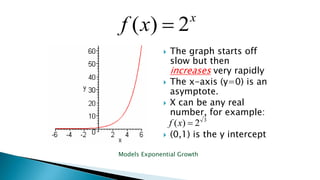
The document discusses the significance of exponential functions in modeling real-life situations such as population growth and decay, as well as compound interest. It explains the differences between exponential functions and other types, emphasizing that the variable is the exponent and provides examples of both exponential growth and decay. The document also outlines methods for solving exponential equations by equating exponents when the bases are equal.

2. The exponential function is very important in
math because it is used to model many real life
situations.
◦ For example: population growth and decay,
compound interest, economics, and much more.

3. Question…
x
b
x
f 
)
(
How is this function
different from functions that
we have worked with
previously?

4. The exponent is the variable!
Answer:
x
b
x
f 
)
(
b = The base
b >0 and b ≠ 1
x = The exponent
x=any real number
Question…
Is f(x)=x3 an exponential
function?
NO

5.  One of the most common exponential functions is
 The graph looks like this:
x
x
f 2
)
( 

6.  The graph starts off
slow but then
increases very rapidly
 The x-axis (y=0) is an
asymptote.
 X can be any real
number, for example:
 (0,1) is the y intercept
x
x
f 2
)
( 
3
2
)
( 
x
f
Models Exponential Growth

7. What would a graph look like if b is
between 0 and 1?
For example: x
x
f 






2
1
)
(
Question…

8.  The graph starts off
very high but then
decreases very rapidly
 The x-axis (y=0) is an
asymptote.
 X can be any real
number, for example:
 (0,1) is the y intercept
x
x
f 






2
1
)
(








2
1
)
(x
f
Models Exponential Decay

9. x
b
x
f 
)
(
b = The base
b >0 and b ≠ 1
x = The exponent
x=any real number
Definition
b>1 0<b<1

11.  What is an exponential equation?
◦ An equation where the variable is the
exponent.
◦ Example:
8
1
2 
x

12. 8
1
2 
x
Any ideas?
What if we changed
the right side to
3
2
3
2
2 

x
Now What?

13. ◦If
◦Then x=?
◦Check:
◦2-3=
3
2
2 

x
3

8
1
Then we have solved
8
1
2 
x

14. 1.Express each side of the equation as a
power of the same base.
2.Set the exponents equal and solve.
3.Check your answer
If the bases are the
same, set the
exponents equal!
Main
idea

15.  Solve for x: x
x 3
2
7
7 

Are the bases equal?
YES
Set the exponents equal.
Solve for x.
x
x 3
2 
 All we have here is a simple
Algebra problem
1


x

16. )
1
(
3
2
)
1
(
7
7 



3
3
7
7 


x
x 3
2
7
7 

x = -1
It checks!

17.  Solve for x: 1
4
25
5 

 t
t
Are the bases equal?
NO
Change the right side to:
1
2
)
5
( 
t
Simplify: 2
2
4
5
5 

 t
t
Solve! 2

t

18. 1
2
2
4
25
5 


1
2
25
5 
1
4
25
5 

 t
t
t = 2
It checks!

19.  Solve for x:
7
7
49 2


x
4
11

x

20.  Solve for x:
7
7
49 2


x
Are the bases equal?
NO
Change both sides to: 2
1
2
2
7
*
7
)
7
( 

x
Simplify: 2
3
4
2
7
7 

x
Solve!
2
3
4
2 

x
4
11

x

21. 2
3
2
4
11
7
49 

2
3
4
3
7
49 
7
7
49 2


x
x = 11/4
It checks!
2
3
4
3
2
7
)
7
( 

22. REVIEW
1. Exponential function:
x
b
x
f 
)
(
The exponent is
the variable
Key Point:
b= the base
b >0 and b ≠1
X= the exponent
X = any real number
2. Exponential Equations: An equation where the
exponent is the variable
Example:
16
2 6
4


x
How to solve:
If the bases are the same,
set the exponents equal!
4
6
4
2
2 

x
Rewrite as:
Set exponents
equal:
4
6
4 

x
Solve: 4
10

x
Check:
16
2
6
)
4
10
(
4


16
2 6
10


16
24

It checks!

23. Homework: Exponential
Equations
Worksheet