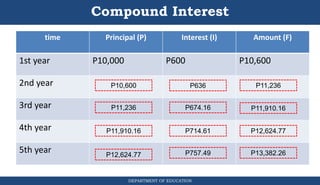
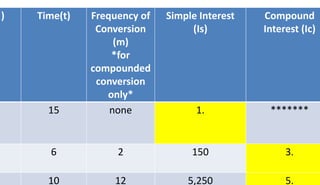
This document provides information about simple and compound interest calculations. It defines key terms like principal, interest rate, and time period. It explains the formulas for calculating simple interest and compound interest, both annually and for other time periods like quarterly or monthly. Sample problems are provided for calculating interest, principal, and future values in simple and compound interest scenarios.

1. STEM - IIIA (MATHEMATICS)
GENERAL MATHEMATICS

2. Content:
BasicBusinessMathematics
Senior High School
Mass Training of Teachers
On Academic Track
STEM III-A (Mathematics)

3. Objectives
DEPARTMENT OF EDUCATION
.
After this session, you are expected to:
1. illustrate simple and compound interests.
2. distinguish between simple and compound
interests.
3. compute interest, maturity value, future value,
and present value in simple interest and
compound interest environment.
4. solve problems involving simple and compound
interests.

4. Lender or creditor- person (or institution)
who invests the money or makes the funds
available
Borrower or debtor- person (or institution)
who owes the money or avails of the funds
from the lender
.
DEPARTMENT OF EDUCATION
.

5. Interest
• income derived from invested capital
• money paid as rental for the use of money
DEPARTMENT OF EDUCATION
.

6. Interest
Interest (I) - a fixed rated proportion as the
rate of interest for any specified time unit.
Interest Rate (r) - ratio of the interest earned
in one time unit to the principal.
Principal or Present Value (P) - refers to the
capital originally invested in a business
transaction.
DEPARTMENT OF EDUCATION
.

7. Interest
Amount / Full Amount/ Maturity or Future
Value (F) - the sum of the Principal (P) and
the Interest (I) due at any time after the
investment of the Principal (P).
Time (t) - period of coverage of the transaction.
Unless otherwise specified, the time unit will
be one year.
DEPARTMENT OF EDUCATION
.

8. Interest
I = Prt
where, I = interest
P = Principal or original
capital invested
r = rate of interest (%)
t = time
DEPARTMENT OF EDUCATION
.

9. Interest
• Simple Interest
• Compound Interest
DEPARTMENT OF EDUCATION
.

10. Ella and Thelma each invest P10,000 for two
years, but under different schemes. Ella’s earns
2% of P10,000 the first year, which is P200, then
another P200 the second year. Thelma earns 2%
of P10,000 the first year, which is P200, the same
as Ella’s. But during the second year, she earns 2%
of the P10,000 and 2% of the P200 also.

11. Ella and Thelma each invest P10,000 for two years, but
under different schemes. Ella’s earns 2% of P10,000 the
first year, which is P200, then another P200 the second
year.
Ella invested on the simple interest.
Thelma earns 2% of P10,000 the first year, which is P200,
the same as Ella’s. But during the second year, she earns
2% of the P10,000 and 2% of the P200 also.
Thelma invested on the compound interest.

12. Simple Interest
DEPARTMENT OF EDUCATION
.
I = Prt
F = P + I
(maturity/future value or full amount)
F = P + Prt
F = P(1 + rt)

13. Simple Interest
I = Prt
DEPARTMENT OF EDUCATION
.
F = P(1 + rt)

14. Simple Interest
DEPARTMENT OF EDUCATION
.
• The unit for time (t) is in year(s).
• When given time (t) is in months, convert it
to year (divide by 12).
• When given time (t) is in days, convert it to
year (divide by 360 or 365).

15. Simple Interest
Sample Problem.
1. Find the interest and the full amount on
P3,000 at 5% interest for two years.
2. Find the principal value P and full amount
F if the investment earns P200 interest in
18 months at the rate of 8%.
DEPARTMENT OF EDUCATION
.
I = P300
F = P3,300
P = P1,666.67
F = P1,866.67

16. Simple Interest
Sample Problem.
3. If P500 is the interest earned of P8,000
which was invested for 16 months, how
much is the rate of interest?
4. How long will it take to accumulate P5,000
to P7,000 if the interest rate is 6%?
DEPARTMENT OF EDUCATION
.
r = 4.70%
t = 6.67 years

17. Simple Interest
DEPARTMENT OF EDUCATION
.
When given time (t) is in days:
Ordinary Interest - all months of the year
are having 30 days, thus 360 days a
year.
Exact Interest - a year has exactly 365
days.

18. Simple Interest
Sample Problem.
1. Find the ordinary and exact interests at 6%
on P3,500 and the corresponding amounts
at the end of 75 days.
DEPARTMENT OF EDUCATION
.

19. Compound Interest
DEPARTMENT OF EDUCATION
.
• If during the term of investment, the interest
due at stated intervals is added to the
principal and thereafter earns interest, the
sum of the increases over the principal by the
end of the term of investment is called
Compound Interest.

20. Compound Interest
DEPARTMENT OF EDUCATION
.
Compound Amount - the total amount due
which consists of the principal and the
compound interest.
Conversion Period - the time between the
successive conversions of interest into
principal.

21. Compound Interest
DEPARTMENT OF EDUCATION
.
Conversion Period - the number of unit of
time in one year as basis for computing
interest which could be either (a) annually,
(b) semi-annualy, (c) quarterly, or (d)
monthly.

22. Compound Interest
DEPARTMENT OF EDUCATION
.
Nominal rate - refers to the rate of borrowing
and is usually quoted as an annual interest
rate, unless otherwise specified.

23. Compound Interest
DEPARTMENT OF EDUCATION
.
Periodic rate or interest rate per
compounding period - refers to the interest
rate per conversion period. It is equal to the
nominal rate divided by the compounding
period in a year.

24. Compound Interest
DEPARTMENT OF EDUCATION
.
Illustration:
Solve for the compound amount and
compound interest at the end of 5 years if
P10,000 is invested at 6% compounded
annually.

25. Compound Interest
DEPARTMENT OF EDUCATION
.
time Principal Interest Amount
1st year
2nd year
3rd year
4th year
5th year

26. Compound Interest
DEPARTMENT OF EDUCATION
.
time Principal (P) Interest (I) Amount (F)
1st year P10,000 P600 P10,600
2nd year
3rd year
4th year
5th year
P10,600 P636 P11,236
P11,236 P674.16 P11,910.16
P11,910.16 P714.61 P12,624.77
P12,624.77 P757.49 P13,382.26

27. Compound Interest
Who will earn more? Group 1 or Group 2?
DEPARTMENT OF EDUCATION
.

28. Compound Interest
Ic =Fc –Pc
Ic =Compound Interest
Fc = Maturity Value
Pc = Present Value
DEPARTMENT OF EDUCATION
.

30. Compound Interest
Sample Problem.
1. Solve for the compound amount and the
compound interest at the end of 2 years if P1,000
is invested at 8% compounded quarterly.
Solution:
Data: P = P1,000
r = 8% or 0.08
m = 4 (quarterly)
t = 2 (years)
DEPARTMENT OF EDUCATION
. F = P1,171.65
I = P171.65

31. Compound Interest
Sample Problem.
2. If P20,000 is invested for 5 years at 12% interest
compounded semi-annually, find the value of F and the
compound interest I.
Solution:
Data: P = P20,000
= 12% or 0.12
m = 2 (semi-annually)
t = 5 years
DEPARTMENT OF EDUCATION
.
F = P35,816.95
I = P15,816.95

33. Compound Interest
1. What is the present value of P50,000 due in 7 years if
money is worth 10% compounded monthly?
Solution:
Data: F = P50,000
r = 10% or 0.1
m = 12 (monthly)
t = 7 (term in 7 yrs.)
DEPARTMENT OF EDUCATION
.
P = P25,657.91

34. ) Time(t) Frequency of
Conversion
(m)
*for
compounded
conversion
only*
Simple Interest
(Is)
Compound
Interest (Ic)
15 none 1. *******
6 2 150 3.
10 12 5,250 5.