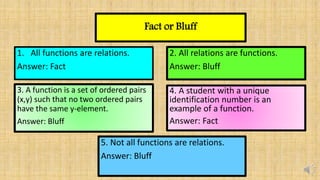
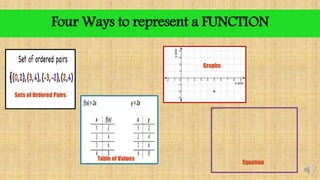
The document discusses evaluating functions. It begins by defining the difference between a function and a relation. It then outlines four ways to represent a function: sets of ordered pairs, tables of values, graphs, and equations. It explains that evaluating a function means replacing the variable x in the function with a given number or expression. Examples are provided to demonstrate how to evaluate different types of functions by performing the substitution. The document concludes with a quiz asking the reader to evaluate sample functions at specific values of x.

1. How to evaluate
?

2. EVALUATING FUNCTIONS
General Math
Week 1, LC Code: (M11GM - Ia – 1)

3. Learning Competency
The learner evaluates a function.
(M11GM - Ia – 1)

4. Learning Objectives
At the end of this video, you are able to:
1. Recall the difference between function and relation;
2. Recall on the four ways to represent a function; and
3. Evaluate a function.

5. What is the difference between
function and relation?
Function
• A function is a relation that is for each
input there is only one output.
• A function is a set of ordered pairs
(x,y) such that no two ordered pairs
have the same x-element (abscissa).
• A function can be a one-to-one or
many-to-one correspondence but can
not be a one-to-many
correspondence.
Relation
• A relation is a set of inputs and
outputs.
• A relation is a set of ordered pairs
(x,y).
• A relation can be one-to-one, one-to-
many and/or many-to-one
correspondence.

6. Fact or Bluff
1. All functions are relations.
Answer: Fact
2. All relations are functions.
Answer: Bluff
3. A function is a set of ordered pairs
(x,y) such that no two ordered pairs
have the same y-element.
Answer: Bluff
4. A student with a unique
identification number is an
example of a function.
Answer: Fact
5. Not all functions are relations.
Answer: Bluff

7. Four Ways to represent a FUNCTION
Sets of Ordered Pairs
Table of Values
Graphs
Equation

8. Which of the following sets of ordered pairs are functions?
Answer: The sets in a and b are functions.
Multiple Choice
a. h = {(0,0),(1,1),(2,2),(3,3),(4,4),...}
d. H = {(0,0),(0,1),(2,2),(3,3),(4,4),...}
b. g = {(0,0),(1,0),(2,0),(3,0),(4,0),...}
c. f = {(-2,0),(-2,1),(-2,2),(-2,3),(-2,4),...}

9. Which of the following tables below represent a
function?
x 0 1 2 3
y 0 1 2 3
x 1 1 1 1
y -4 -2 0 2
x -1 0 1 2
y 2 2 2 2
x 2 4 2 4
y -2 0 2 6
Answer: A and C
A
B
C
D

10. Which of the following graphs can be graphs of
functions?
Answer: a, b and c

11. Which of the following equations represent a
function?
Answer: a, c and d
𝒃. 𝒙𝟐
+ 𝒚𝟐
= 𝟏 d. 𝒚 = 𝟏𝟎𝟎𝒙
𝒂. 𝒚 = 𝟐𝒙𝟐 − 𝟐𝒙 + 𝟐 c. 𝒚 = 𝟐𝒙 + 𝟏

12. Evaluating a function means replacing the variable x in the function
with a given number or expression.
For example, evaluate the function 𝑓 𝑥 = 2𝑥 + 4 𝑓𝑜𝑟 𝑥 = 5.
Just replace the variable “x” with “5”:
𝑓 5 = 2 5 + 4 = 14
Answer: f(5)=14
Evaluating Functions

13. The function f is define on the real numbers by
𝑓 𝑥 = 2 + 𝑥 − 𝑥2
. What is the value of 𝑓 −3 ?
Solution:
𝑓 𝑥 = 2 + 𝑥 − 𝑥2, 𝑓 −3 =?
𝑓 −3 = 2 + (−3) − (−3)2 substitute x with -3
𝑓 −3 = 2 + −3 − 9 simplify (−32)
𝑓 −3 = −10
The value of 𝑓 −3 is − 10.

14. The function 𝑔 is define on the real numbers by
g 𝑥 = (𝑥2
+ 1)(3𝑥 − 5). What is the value of g 4 ?
Solution:
g 𝑥 = (𝑥2 + 1)(3𝑥 − 5), g 4 =?
g 4 = 42 + 1 [3(4) − 5], substitute x with 4
g 4 = (16 + 1)(12 − 5), simplify 42 , multiply 3(4)
g 4 = (17)(7), add (16 + 1), subtract (12 - 5)
g 4 = 119
The value of 𝑔 4 is 119.

15. Quiz
Evaluate the following functions at 𝑥 = 2.
1. 𝑓 𝑥 = 2𝑥 + 1
2. 𝑞 𝑥 = 𝑥2 − 2𝑥 + 2
3. 𝑔 𝑥 = 𝑥 + 7
4. 𝑟 𝑥 =
6𝑥−2
𝑥+3
5. 𝑟 𝑥 = 4𝑥 − 1
Answer:
1. 𝑓 2 = 2𝑥 + 1= 2(2)+1 = 4 + 1 = 5
2. 𝑞 2 = 𝑥2
− 2𝑥 + 2 = 22
− 2 2 + 2 = 4 − 4 + 2 = 2
3. 𝑔 2 = 𝑥 + 7 = 2 + 7 = 9 = ±3
4. 𝑟 2 =
6𝑥−2
𝑥+3
=
6 2 −2
2+3
=
12−2
5
=
10
5
= 2
5. 𝑟 𝑥 = 4𝑥 − 1 = 42 − 1 = 16 − 1 = 15