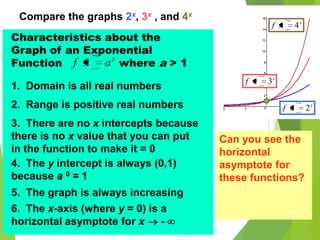
This document contains information from multiple slideshare presentations on exponential functions accessed on March 3rd, 2014. It discusses key properties of exponential functions including constant growth rates, domains of positive real numbers, and horizontal asymptotes. Examples are provided of evaluating exponential equations by setting exponents equal when bases can be written the same, and using logarithms when bases are different. Applications covered include modeling internet traffic growth and compound interest calculations.