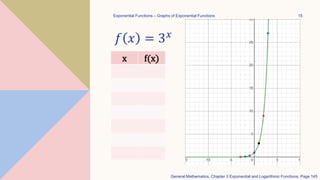
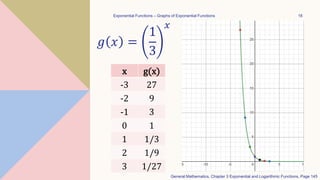
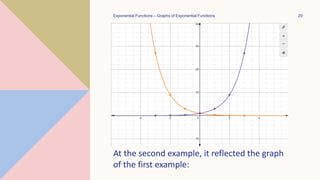
This document discusses exponential functions. It defines exponents as showing how many times a variable is multiplied by itself. An exponential function is defined as f(x)=ax, where a is the base and must be greater than 0 and not equal to 1. Exponential functions are evaluated by calculating the base raised to the power of x. The graph of an exponential function f(x)=ax is a curve that increases rapidly as x increases. The graph of f(x)=1/ax is the reflection of f(x)=ax across the y-axis, as 1/ax = a-x.

1. EXPONENTIAL
FUNCTIONS
General Mathematics

2. EXPONENTS
An exponent is a term used that shows how
many times a variable or a number is being
multiplied to itself.
Exponential Functions 2

3. EXPONENTS
An exponent is a term used that shows how
many times a variable or a number is being
multiplied to itself.
Exponential Functions 3
𝑥𝑛 = 𝑥 ∗ 𝑥 ∗ 𝑥 ∗ ⋯ 𝑥
24 = 2 ∗ 2 ∗ 2 ∗ 2 = 16
55 = 5 ∗ 5 ∗ 5 ∗ 5 ∗ 5 = 3,125

4. FUNCTIONS
A function (f) is a rule that assigns to each
element x in a set A exactly one element
called f(x), in a set B. It has two parts, the
Domain and the Range.
Exponential Functions 4
General Mathematics, Page 3

5. FUNCTIONS
A function (f) is a rule that assigns to each
element x in a set A exactly one element
called f(x), in a set B. It has two parts, the
Domain and the Range.
Exponential Functions 5
𝑓 𝑥 = 2𝑥
𝑓 3 = 2𝑥 = 2 3 = 6
𝑓 𝑥 + 1 = 2𝑥 = 2 𝑥 + 1 = 2𝑥 + 2

6. EXPONENTIAL
FUNCTION
Definition and Concepts

7. EXPONENTIAL
FUNCTIONS
The exponential function with base a is
defined for al real numbers x by
f(x)=ax
Where a>0 and a≠1
Exponential Functions 7
General Mathematics, Chapter 3 Exponential and Logarithmic Functions, Page 144

8. a ≠ 1
We assume that a≠1 because the function
f(x) = 1x = 1 is just a constant function.
Exponential Functions 8
General Mathematics, Chapter 3 Exponential and Logarithmic Functions, Page 145
a > 0
In Real Analysis, the base of an exponential is
defined for all positive real values excluding
1.
Why can’t the base of the exponential function be less than zero? - Quora

9. EXPONENTIAL
FUNCTION
Evaluation

10. 𝑓 𝑥 = 3𝑥
Exponential Functions – Evaluating Exponential Functions 10
General Mathematics, Chapter 3 Exponential and Logarithmic Functions, Page 145
𝐿𝑒𝑡 𝑓 𝑥 𝑏𝑒 𝑓 5
𝑓 5 = 35
𝑓 5 = 3 ∗ 3 ∗ 3 ∗ 3 ∗ 3
𝑓 5 = 243
𝐿𝑒𝑡 𝑓 𝑥 𝑏𝑒 𝑓 3
𝑓 3 = 33
𝑓 3 = 3 ∗ 3 ∗ 3
𝑓 3 = 27

11. 𝑓 𝑥 = 3𝑥
Exponential Functions – Evaluating Exponential Functions 11
General Mathematics, Chapter 3 Exponential and Logarithmic Functions, Page 145
𝐿𝑒𝑡 𝑓 𝑥 𝑏𝑒 𝑓 −5
𝑓 −5 = 3−5
𝑓 −5 =
1
35
𝑓 −5 =
1
243
𝐿𝑒𝑡 𝑓 𝑥 𝑏𝑒 𝑓 −3
𝑓 −3 = 3−3
𝑓 −3 =
1
33
𝑓 −3 =
1
27

12. EXPONENTIAL
FUNCTION
Plotting and Graphing

13. 𝑓 𝑥 = 3𝑥
Exponential Functions – Graphs of Exponential Functions 13
General Mathematics, Chapter 3 Exponential and Logarithmic Functions, Page 145
x f(x)
-3 1/27
-2 1/9
-1 1/3
0 1
1 3
2 9
3 27
x f(x)

14. 𝑓 𝑥 = 3𝑥
Exponential Functions – Graphs of Exponential Functions 15
General Mathematics, Chapter 3 Exponential and Logarithmic Functions, Page 145
x f(x)
-3 1/27
-2 1/9
-1 1/3
0 1
1 3
2 9
3 27
x f(x)

15. 𝑔 𝑥 =
1
3
𝑥
Exponential Functions – Graphs of Exponential Functions 17
General Mathematics, Chapter 3 Exponential and Logarithmic Functions, Page 145
x g(x)
-3 27
-2 9
-1 3
0 1
1 1/3
2 1/9
3 1/27

16. 𝑔 𝑥 =
1
3
𝑥
Exponential Functions – Graphs of Exponential Functions 18
General Mathematics, Chapter 3 Exponential and Logarithmic Functions, Page 145
x g(x)
-3 27
-2 9
-1 3
0 1
1 1/3
2 1/9
3 1/27

17. NOTICE THAT…
At the second example, it reflected the graph
of the first example:
Exponential Functions – Graphs of Exponential Functions 19

18. At the second example, it reflected the graph
of the first example:
Exponential Functions – Graphs of Exponential Functions 20

19. NOTICE THAT…
At the second example, it reflected the graph
of the first example:
Exponential Functions – Graphs of Exponential Functions 21
𝑔 𝑥 =
1
3
𝑥
=
1
3𝑥
= 3−𝑥 = 𝑓(−𝑥)
Thus, making the second example as the
reflection of the first example.
General Mathematics, Chapter 3 Exponential and Logarithmic Functions, Page 146