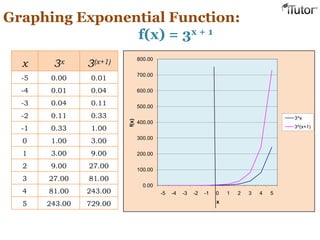
This document discusses exponential functions. It defines exponential functions as functions where f(x) = ax + B, where a is a real constant and B is any expression. Examples of exponential functions given are f(x) = e-x - 1 and f(x) = 2x. The document also discusses evaluating exponential equations with like and different bases using logarithms. It provides examples of graphing exponential functions and discusses the key characteristics of functions of the form f(x) = bx, including their domains, ranges, and asymptotic behavior. The document concludes with an example of applying exponential functions to model compound interest.

1. Exponential
Functions
T- 1-855-694-8886
Email- info@iTutor.com
By iTutor.com

2. Exponential Function
 An exponential equation is an equation in which
the variable appears in an exponent.
 Exponential functions are functions where
f(x) = ax + B,
where a is any real constant and B is any expression.
For example,
f(x) = e-x - 1 is an exponential function.
 Exponential Function:
f(x) = bx or y = bx,
where b > 0 and b ≠ 1 and x is in R
For example,
f(x) = 2x
g(x) = 10x
h(x) = 5x+1

3. NOT Exponential Functions
 f(x) = x2
– Base, not exponent, is variable
 g(x) = 1x
– Base is 1
 h(x) = (-3)x
– Base is negative
 j(x) = xx
– Base is variable

4. Exponential Equations with Like Bases
 Example #1 - One exponential expression.
 Example #2 - Two exponential expressions.
Evaluating Exponential Function
32x 1
5 4
32x 1
9
32x 1
32
2x 1 2
2x 1
x
1
2
1. Isolate the exponential
expression and rewrite the
constant in terms of the same
base.
2. Set the exponents equal to
each other (drop the bases) and
solve the resulting equation.
3x 1
9x 2
3x 1
32 x 2
3x 1
32x 4
x 1 2x 4
x 5

5. Exponential Equations with Different Bases
 The Exponential Equations below contain exponential
expressions whose bases cannot be rewritten as the same
rational number.
 The solutions are irrational numbers, we will need to use
a log function to evaluate them.
 Example #1 - One exponential expression.
32x 1
5 11 or 3x 1
4x 2
32 x 1
5 11
32 x 1
16
ln 32x 1
ln 16
(2x 1)ln3 ln16
1. Isolate the exponential expression.
3. Use the log rule that lets you
rewrite the exponent as a multiplier.
2. Take the log (log or ln) of both
sides of the equation.

6. Graphing Exponential Function:
f(x) = 3x + 1
0.00
100.00
200.00
300.00
400.00
500.00
600.00
700.00
800.00
-5 -4 -3 -2 -1 0 1 2 3 4 5
f(x)
x
3^x
3^(x+1)
x 3x 3(x+1)
-5 0.00 0.01
-4 0.01 0.04
-3 0.04 0.11
-2 0.11 0.33
-1 0.33 1.00
0 1.00 3.00
1 3.00 9.00
2 9.00 27.00
3 27.00 81.00
4 81.00 243.00
5 243.00 729.00

7. Characteristics of f(x) = bx
0.00
5.00
10.00
15.00
20.00
25.00
30.00
35.00
-5 -4 -3 -2 -1 0 1 2 3 4 5
f(x)
x
2^x
(0.5)^x
x 2x (0.5)x
-5 0.03 32.00
-4 0.06 16.00
-3 0.13 8.00
-2 0.25 4.00
-1 0.50 2.00
0 1.00 1.00
1 2.00 0.50
2 4.00 0.25
3 8.00 0.13
4 16.00 0.06

8.  Domain of f(x)
= {- ∞ , ∞}
 Range of f(x)
= (0, ∞ )
 bx passes through (0, 1)
 For b>1, rises to right
For 0<b<1, rises to left
 bx approaches, but does not
touch, x-axis, (x-axis called
an assymptote)
0.00
5.00
10.00
15.00
20.00
25.00
30.00
35.00
-5 -4 -3 -2 -1 0 1 2 3 4 5
f(x)
x
2^x
(0.5)^x
Characteristics of f(x) = bx

9. Application: Compound Interest
 Suppose:
- A: amount to be received
P: principal
r: annual interest (in decimal)
n: number of compounding periods per year
t: years
n
n
r
ptA 1)(
Example
 What would be the yield for the following investment?
P = 8000, r = 7%, n = 12, t = 6 years
612
12
07.0
18000A ≈ $12,160.84

10. The End
Call us for more
information:
www.iTutor.com
1-855-694-8886
Visit