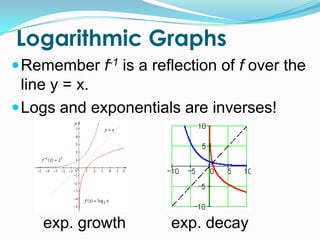
Logarithms were invented to solve exponential equations like 2x = 6, where x is between 2 and 3. A logarithm with base b is defined as logby = x if and only if bx = y. Common properties of logarithms include logb1 = 0 and logbb = 1. Logarithmic functions have inverse relationships with exponential functions and can be graphed by shifting and reflecting the standard logarithmic curve.

2. What is a Logarithm?
 We know 22 = 4 and 23 = 8, but for what
value of x does 2x = 6?
 It must be between 2 and 3…
 Logarithms were invented to solve
exponential equations like this.
 x = log26 ≈ 2.585

3. Logarithms with Base b
 Let b and y be positive numbers and b≠1.
 The logarithm of y with base b is written
logby and is defined:
logby = x if and only if bx = y

4. Rewriting Log Equations
 Write in exponential form:
 log2 32 = 5
 log5 1 = 0
 log10 10 = 1
 log10 0.1 = -1
 log1/2 2 = -1

5. Special Log Values
 For positive b such that b ≠ 1:
 Logarithm of 1: logb 1 = 0 since b0 = 1
 Logarithm of base b: logb b = 1 since b1 = b

6. Evaluating Log Expressions
 To find logb y, think “what power of b will
give me y?”
 Examples:
 log3 81
 log1/2 8
 log9 3

7. Your Turn!
 Evaluate each expression:
 log4 64
 log32 2

8. Common and Natural Logs
 Common Logarithm - the log with base 10
 Written “log10” or just “log”
 log10 x = log x
 Natural Logarithm – the log with base e
 Can write “loge“ but we usually use “ln”
 loge x = ln x

9. Evaluating Common and
Natural Logs
 Use “LOG” or “LN” key on calculator.
 Evaluate. Round to 3 decimal places.
 log 5
 ln 0.1

10. Evaluating Log Functions
 The slope s of a beach is related to the
average diameter d (in mm) of the sand
particles on the beach by this equation:
s = 0.159 + 0.118 log d
Find the slope of a beach if the average
diameter of the sand particles is 0.25 mm.

11. Inverses
 The logarithmic function g(x) = logb x
is the inverse of the exponential function
f(x) = bx.
 Therefore:
g(f(x)) = logb bx = x and f(g(x)) = blogb x = x
 This means they “undo” each other.

12. Using Inverse Properties
 Simplify:
 10logx
 log4 4x
 9log9 x
 log3 9x

13. Your Turn!
 Simplify:
 log5 125x
 5log5 x

14. Finding Inverses
 Switch x and y, then solve for y.
 Remember: to “chop off a log” use the
“circle cycle”!
 Find the inverse:
y = log3 x y = ln(x + 1)

15. Your Turn!
 Find the inverse.
 y = log8 x
 y = ln(x – 3)

16. Logarithmic Graphs
 Remember f-1 is a reflection of f over the
line y = x.
 Logs and exponentials are inverses!
exp. growth exp. decay

17. Properties of Log Graphs
 General form: y = logb (x – h) + k
 Vertical asymptote at x = h.
(x = 0 for parent graph)
 Domain: x > h
 Range: All real #s
 If b > 1, graph moves up to the right
 If 0 < b < 1, graph moves down to the
right.

18. To graph:
 Sketch parent graph (if needed).
 Always goes through (1, 0) and (b, 1)
 Choose one more point if needed.
 Don’t cross the y-axis!
 Shift using h and k.
 Be Careful: h is in () with the x, k is not

19. Examples:
 Graph. State the domain and range.
y = log1/3 x – 1
Domain:
Range:

20.  Graph. State the domain and range.
y = log5 (x + 2)
Domain:
Range:

21. Your Turn!
 Graph. State the domain and range.
y = log3 (x + 1)
Domain:
Range: