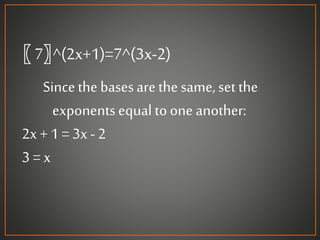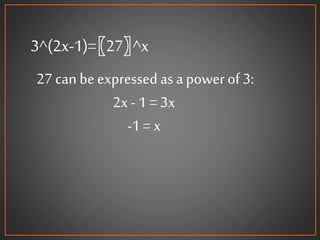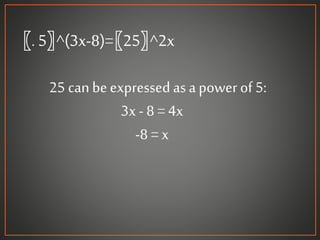An exponential equation is one where a variable appears in the exponent. To solve exponential equations without logarithms, both sides must have comparable exponential expressions with the same base, so the powers can be set equal. If both sides can be expressed as powers of the same base b, the property b^x = b^y implies x = y can be used to set the exponents equal and solve for the variable. This demonstrates how exponential equations are solved by setting the powers equal when the bases are the same. For equations that cannot be expressed with a common base, logarithms are used.

2. An exponential equation is one in
which a variable occurs in the
exponent.

3. To solve exponentialequations without logarithms,you
needto have equationswith comparable exponential
expressions oneither side of the "equals" sign,so youcan
compare the powers and solve. In other words,you have
to have "(some base) to (some power)equals (the same
base) to (some other power)", where youset the two
powers equal to each other, and solve the resulting
equation

4. An exponential equation in which each
side can beexpressed in
terms of the same base can be solved
using the property:
if 𝑏 𝑥
=𝑏 𝑦
, thenx=y (whereb >0 and
b≠1)

5. If youcan express bothsides of the
equation as powers of the same base,
you can set the exponents equal to solve
for x.

6. 〖 7〗^(2x+1)=7^(3x-2)
Sincethe basesarethe same,set the
exponentsequal toone another:
2x + 1 = 3x- 2
3 = x

7. 3^(2x-1)=〖27〗^x
27 can beexpressed as apowerof 3:
2x - 1 = 3x
-1 = x

8. 〖. 5〗^(3x-8)=〖25〗^2x
25 canbeexpressed as apowerof 5:
3x- 8 = 4x
-8 = x

9. Solve 5x = 53
Sincethe bases("5" in eachcase)arethesame,
then the only way thetwo expressionscould be
equalis for thepowers alsoto bethe same.That
is:
x = 3

10. This solution demonstrates howthis entireclass
of equation is solved: if the bases arethe same,
then the powers must alsobe the same, in order
for the two sidesof the equation to be equalto
eachother. Sincethe powers must bethe same,
then you can set the two powers equal to each
other, and solve the resulting equation.

11. Unfortunately,not allexponentialequations can
beexpressedin termsof a common base. For
theseequations,logarithms areused toarriveat a
solution. (Youmay solve using common log or
naturalln.)

12. To solve most exponentialequations:
1. Isolate the exponentialexpression.
2. Take log orlnof bothsides.
3. Solve for the variable.