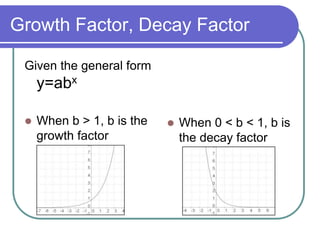
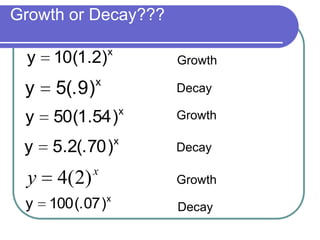
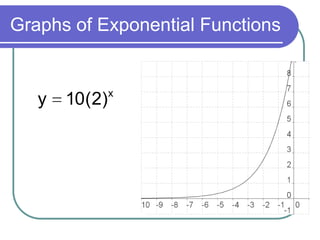
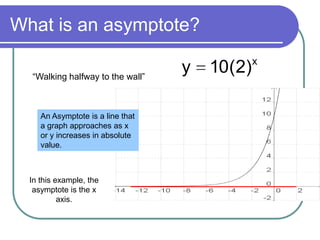
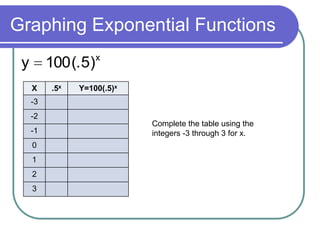
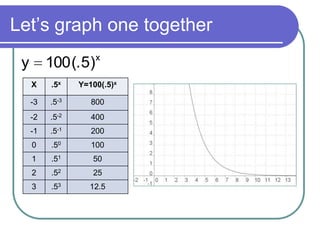
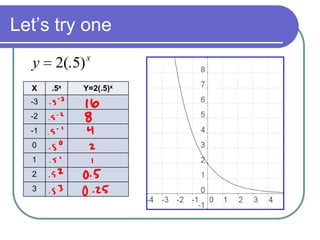
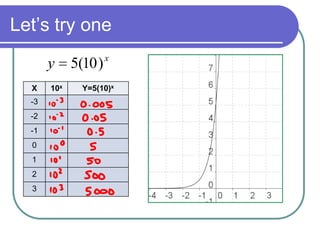
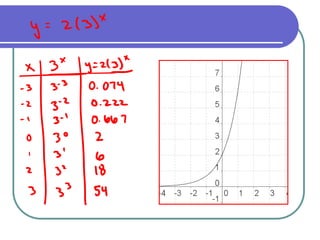
This document discusses exponential functions and equations. It defines exponential equations as having the general form y=abx, where a and b are constants and b can represent either a growth or decay factor depending on whether it is greater than or less than 1. The document provides examples of graphing exponential functions from tables of values. It also demonstrates how to write an exponential equation given two points by solving for the constants a and b. Finally, it shows how to model real-world growth scenarios using exponential equations.

1. 7.2 Exploring Exponential
Models

2. What is an exponential equation?
An exponential equation has the general form
y=abx
1band0b,0wherea

3. Growth Factor, Decay Factor
Given the general form
y=abx
 When b > 1, b is the
growth factor
 When 0 < b < 1, b is
the decay factor

4. Growth or Decay???
x
)2.1(10y
x
)9(.5y
x
)54.1(50y
x
)70(.2.5y
x
y )2(4
x
)07(.100y
Growth
Decay
Growth
Decay
Growth
Decay

5. Graphs of Exponential Functions
x
)2(10y

6. What is an asymptote?
x
)2(10y“Walking halfway to the wall”
An Asymptote is a line that
a graph approaches as x
or y increases in absolute
value.
In this example, the
asymptote is the x
axis.

7. Graphing Exponential Functions
x
)5(.100y
X .5x Y=100(.5)x
-3
-2
-1
0
1
2
3
Complete the table using the
integers -3 through 3 for x.

8. Let’s graph one together
x
)5(.100y
X .5x Y=100(.5)x
-3 .5-3 800
-2 .5-2 400
-1 .5-1 200
0 .50 100
1 .51 50
2 .52 25
3 .53 12.5

9. Let’s try one
x
y )5(.2
X .5x Y=2(.5)x
-3
-2
-1
0
1
2
3
Complete the table using the
integers -3 through 3 for x. Then
graph the function.

10. Let’s try one
x
y )5(.2
X .5x Y=2(.5)x
-3
-2
-1
0
1
2
3

11. Let’s try one
x
y )10(5
X 10x Y=5(10)x
-3
-2
-1
0
1
2
3
Complete the table using the
integers -3 through 3 for x. Then
graph the function.

12. Let’s try one
x
y )10(5
X 10x Y=5(10)x
-3
-2
-1
0
1
2
3

13. Writing Exponential Equations
 Find the exponential equation passing through
the points (3,20) and (1,5).
x
aby
a
b3
20
1
3
20
5 b
b
31
205 b
3
20 ab
Start with the general form.
Choose a point. Substitute for x and y using (3, 20)
Solve for a
Substitute x and y using (1, 5) and a using a
b3
2
Division property of exponents

14. Writing Exponential Equations
 Find the exponential equation passing through
the points (3,20) and (1,5).
2
4
5
20
20
5
205
2
2
2
b
b
b
b
Simplify
Solve for b
2
5
8
20
2
2020
33
b
a
Go back to the equation for a; substitute
in b and solve for a

15. Writing Exponential Equations
 Find the exponential equation passing through
the points (3,20) and (1,5).
x
aby
x
y )2(
2
5
Going back to the general form,
substitute in a and b
The exponential equation passing through
the points (3,20) and (1,5) is x
y )2(
2
5

16. Let’s Try One
 Find the exponential equation passing through
the points (2,4) and (3,16).
x
aby
a
b2
4
3
2
4
16 b
b
23
416 b
2
4 ab
Start with the general form.
Choose a point. Substitute for x and y using (2, 4)
Solve for a
Substitute x and y using (3, 16) and a using a
b2
4
Division property of exponents

17. Writing Exponential Equations
1
416 b
4b
Simplify
Solve for b
25.0
4
1
4
4
2
a
Go back to the equation for a; substitute in
b and solve for a
x
aby
x
y )4(25.0 Going back to the general form,
substitute in a and b
The exponential equation passing through
the points (2,4) and (3,16) is
x
y )4(25.0

18. Putting it all together . . .
 Find the equation of the exponential
function that goes through
(1,6) and (0,2). Graph the function.

21. Modeling Growth with an
Exponential Equation
 The growth factor can be found in word
problems using b = 1 + r
where r = rate or amount of increase.
You can substitute your new b into your
general equation to find the exponential
function.

22.  EX- a guy puts $1000 into a simple 3%
interest account. What is the exponential
equation?
x
y )03.1(1000
r = rate 3% (write as 0.03)
b = 1 + r = 1.03
x = time
a = amount put into the account
($1,000)
x
aby

23.  EX – a colony of 1000 bacteria cells
doubles every hour. What is the
exponential equation?
r = 1 (why not 2?)
b = r + 1 = 2
x = time (in hours)
a = the original number in the
colony (1,000 bacteria )
x
y )2(1000
x
aby
b = r + 1, where r is the amount of
increase. We are increasing by 100%
each time something doubles, so r = 1

24.  EX- a $15000 car depreciates at 10% a
year. What is the exponential equation?
r = - 10% (the car is worth 10%
less each year)
b = 1 - r = 1 – 0.1 = 0.9
x = time (in years)
a = amount put into the account
($15,000)
x
y )9.0(15000
x
aby