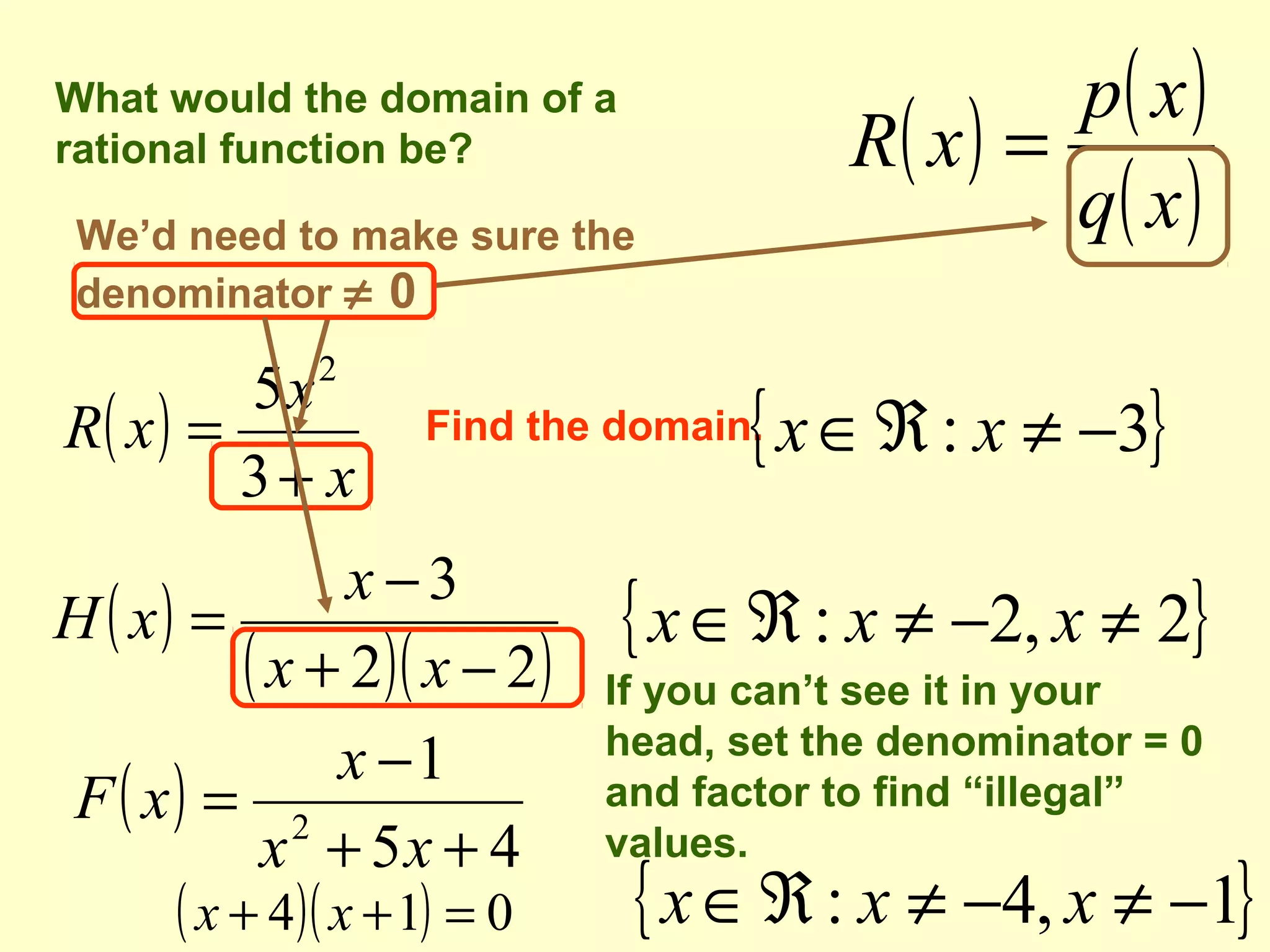
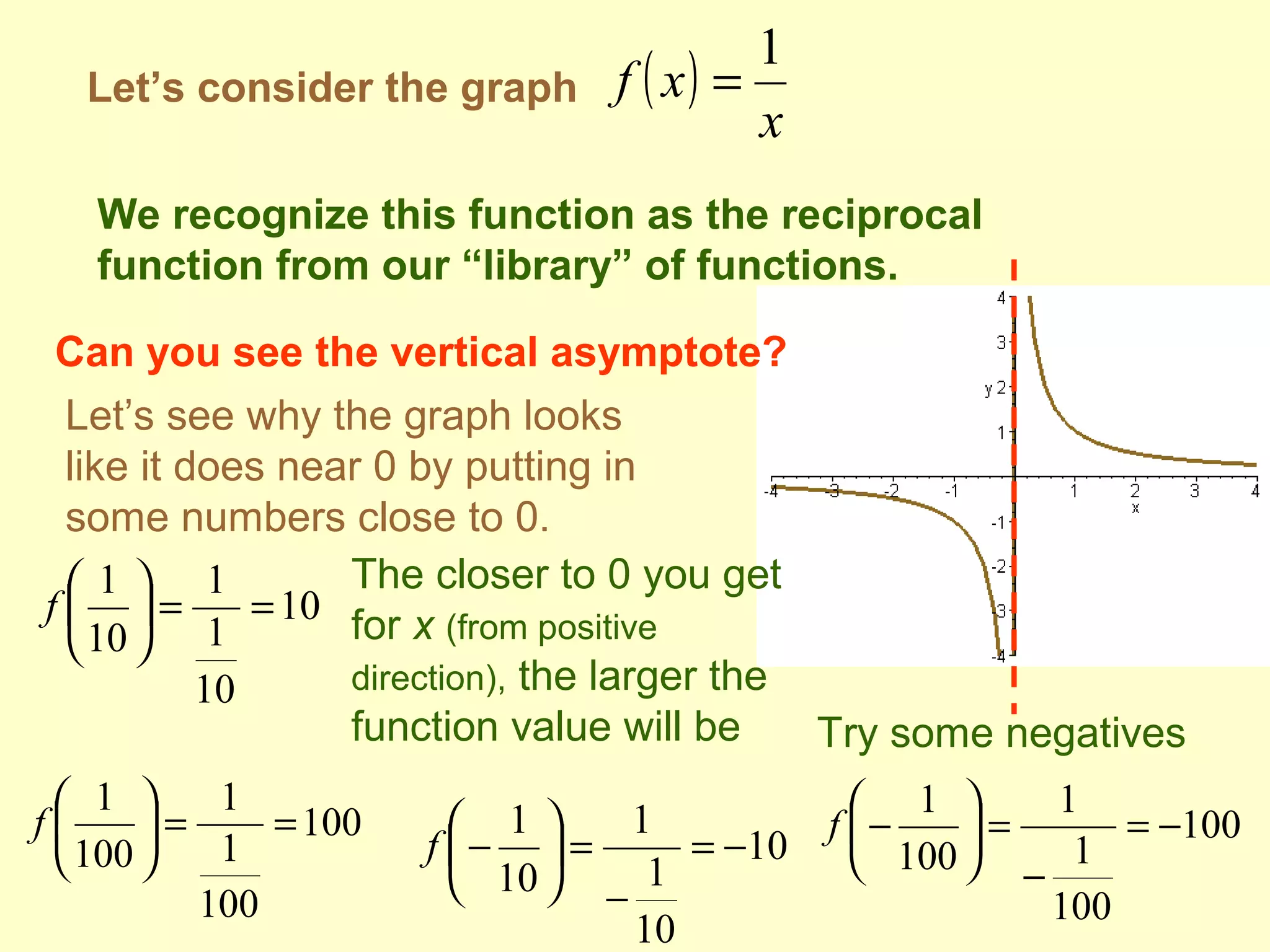
This document discusses rational functions and their graphs. It defines a rational function as a function of the form f(x) = p(x)/q(x) where p and q are polynomials. It explains that the domain of a rational function excludes any values that would make the denominator equal to 0. It describes how to find vertical, horizontal, and oblique asymptotes of a rational function by comparing the degrees of the polynomials in the numerator and denominator. Vertical asymptotes occur where the denominator is 0, and horizontal or oblique asymptotes depend on whether the degree of the numerator is less than, equal to, or greater than the degree of the denominator. Examples are provided to illustrate these concepts.

1. RATIONAL
FUNCTIONS
A rational function is a function of the form:
( ) ( )
( )xq
xp
xR = where p and q
are polynomials

2. ( ) ( )
( )xq
xp
xR =
What would the domain of a
rational function be?
We’d need to make sure the
denominator ≠ 0
( )
x
x
xR
+
=
3
5 2
Find the domain.{ }3: −≠ℜ∈ xx
( )
( )( )22
3
−+
−
=
xx
x
xH { }2,2: ≠−≠ℜ∈ xxx
( )
45
1
2
++
−
=
xx
x
xF
If you can’t see it in your
head, set the denominator = 0
and factor to find “illegal”
values.
( )( ) 014 =++ xx { }1,4: −≠−≠ℜ∈ xxx

3. The graph of looks like this:( ) 2
1
x
xf =
Since x ≠ 0, the graph approaches 0 but never crosses or
touches 0. A vertical line drawn at x = 0 is called a
vertical asymptote. It is a sketching aid to figure out the
graph of a rational function. There will be a vertical
asymptote at x values that make the denominator = 0
If you choose x values close to 0, the graph gets
close to the asymptote, but never touches it.

4. Let’s consider the graph ( )
x
xf
1
=
We recognize this function as the reciprocal
function from our “library” of functions.
Can you see the vertical asymptote?
Let’s see why the graph looks
like it does near 0 by putting in
some numbers close to 0.
10
10
1
1
10
1
==





f
100
100
1
1
100
1
==





f
10
10
1
1
10
1
−=
−
=





−f
100
100
1
1
100
1
−=
−
=





−f
The closer to 0 you get
for x (from positive
direction), the larger the
function value will be Try some negatives

5. Does the function have an x intercept?( )
x
xf
1
=
There is NOT a value that you can plug in for x that
would make the function = 0. The graph approaches
but never crosses the horizontal line y = 0. This is
called a horizontal asymptote.
A graph will NEVER cross a
vertical asymptote because the
x value is “illegal” (would make
the denominator 0)
x
1
0 ≠
A graph may cross a horizontal
asymptote near the middle of
the graph but will approach it
when you move to the far right
or left

6. Graph ( )
x
xQ
1
3+=
This is just the reciprocal function transformed. We can
trade the terms places to make it easier to see this.
3
1
+=
x
vertical translation,
moved up 3
( )
x
xf
1
=
( )
x
xQ
1
3+=
The vertical asymptote
remains the same because in
either function, x ≠ 0
The horizontal asymptote
will move up 3 like the graph
does.

7. Finding Asymptotes
VERTICALASYMPTOTES
There will be a vertical asymptote at any
“illegal” x value, so anywhere that would make
the denominator = 0
( )
43
52
2
2
−−
++
=
xx
xx
xR
Let’s set the bottom = 0
and factor and solve to
find where the vertical
asymptote(s) should be.
( )( ) 014 =+− xx
So there are vertical
asymptotes at x = 4
and x = -1.

8. If the degree of the numerator is
less than the degree of the
denominator, (remember degree
is the highest power on any x
term) the x axis is a horizontal
asymptote.
If the degree of the numerator is
less than the degree of the
denominator, the x axis is a
horizontal asymptote. This is
along the line y = 0.
We compare the degrees of the polynomial in the
numerator and the polynomial in the denominator to tell
us about horizontal asymptotes.
( )
43
52
2
+−
+
=
xx
x
xR
degree of bottom = 2
HORIZONTAL ASYMPTOTES
degree of top = 1
1
1 < 2

9. If the degree of the numerator is
equal to the degree of the
denominator, then there is a
horizontal asymptote at:
y = leading coefficient of top
leading coefficient of bottom
degree of bottom = 2
HORIZONTAL ASYMPTOTES
degree of top = 2
The leading coefficient
is the number in front of
the highest powered x
term.
horizontal asymptote at:
1
2=
( )
43
542
2
2
+−
++
=
xx
xx
xR
1
2
=y

10. ( )
43
532
2
23
+−
+−+
=
xx
xxx
xR
If the degree of the numerator is
greater than the degree of the
denominator, then there is not a
horizontal asymptote, but an
oblique one. The equation is
found by doing long division and
the quotient is the equation of
the oblique asymptote ignoring
the remainder.
degree of bottom = 2
OBLIQUE ASYMPTOTES
degree of top = 3
532 23
+−+ xxx432
−− xx
remaindera5 ++x
Oblique asymptote
at y = x + 5

11. SUMMARY OF HOW TO FIND ASYMPTOTES
Vertical Asymptotes are the values that are NOT in the
domain. To find them, set the denominator = 0 and solve.
To determine horizontal or oblique asymptotes, compare
the degrees of the numerator and denominator.
1. If the degree of the top < the bottom, horizontal
asymptote along the x axis (y = 0)
2. If the degree of the top = bottom, horizontal asymptote
at y = leading coefficient of top over leading
coefficient of bottom
3. If the degree of the top > the bottom, oblique
asymptote found by long division.

12. Acknowledgement
I wish to thank Shawna Haider from Salt Lake Community College, Utah
USA for her hard work in creating this PowerPoint.
www.slcc.edu
Shawna has kindly given permission for this resource to be downloaded
from www.mathxtc.com and for it to be modified to suit the Western
Australian Mathematics Curriculum.
Stephen Corcoran
Head of Mathematics
St Stephen’s School – Carramar
www.ststephens.wa.edu.au