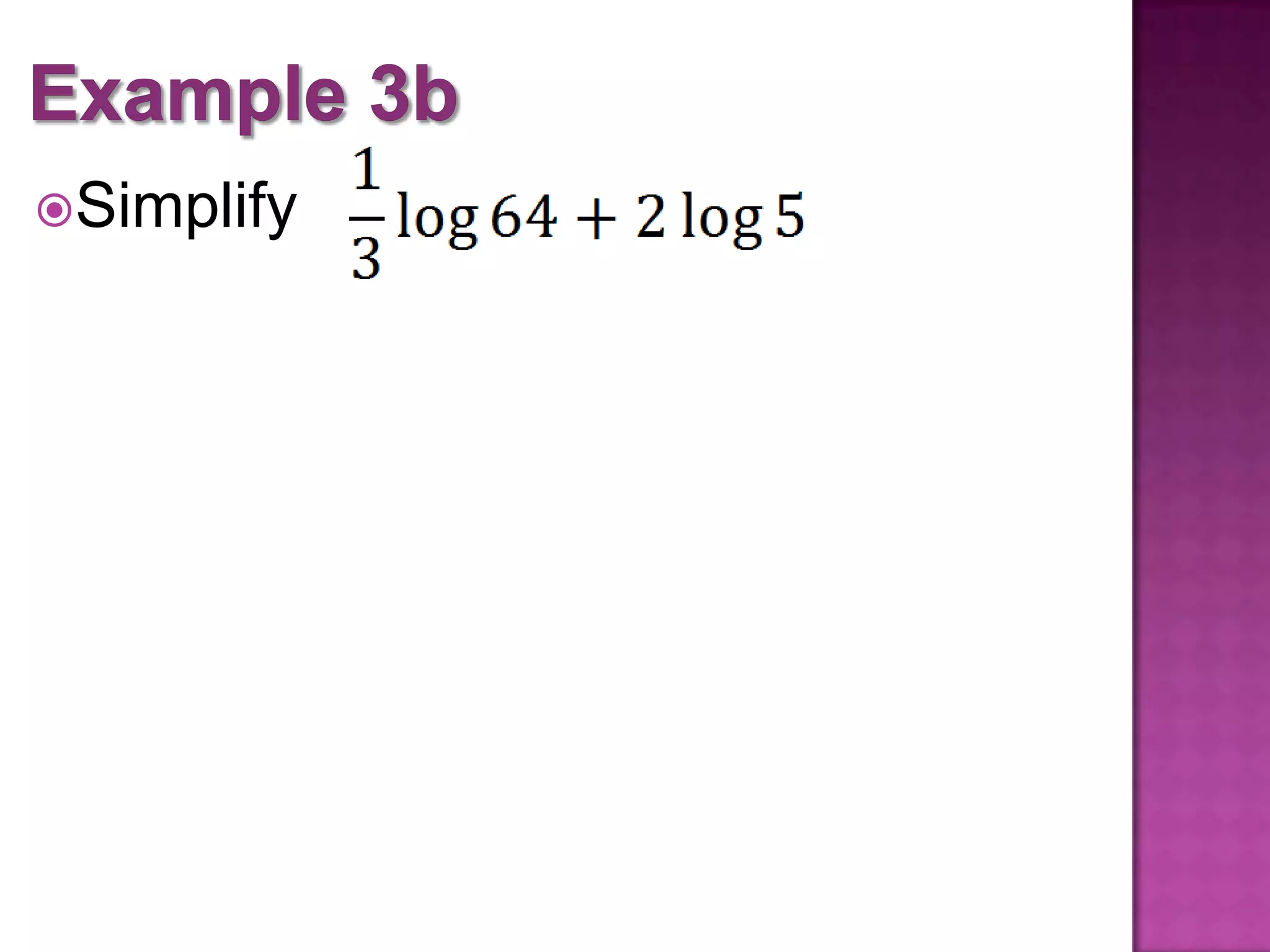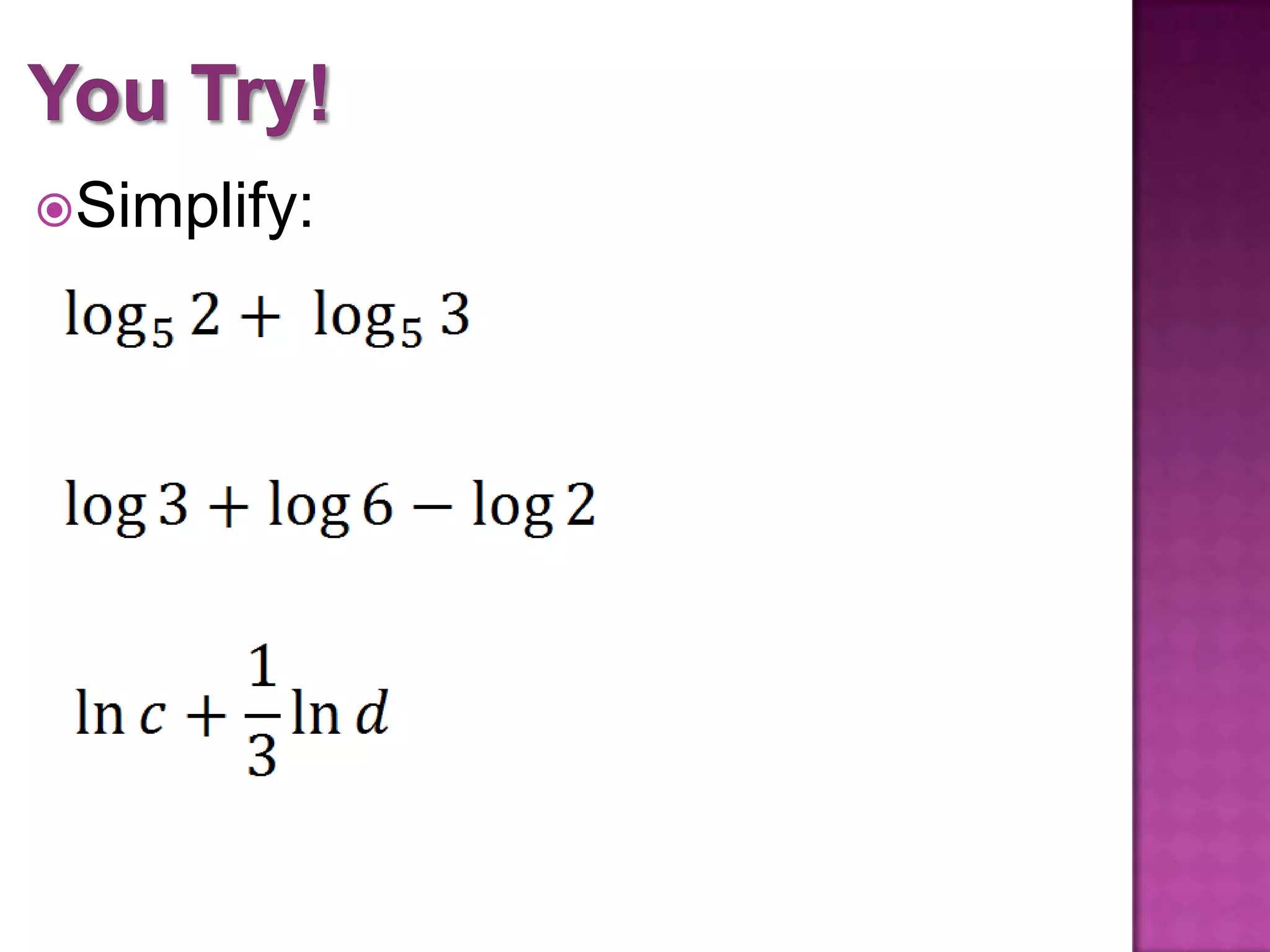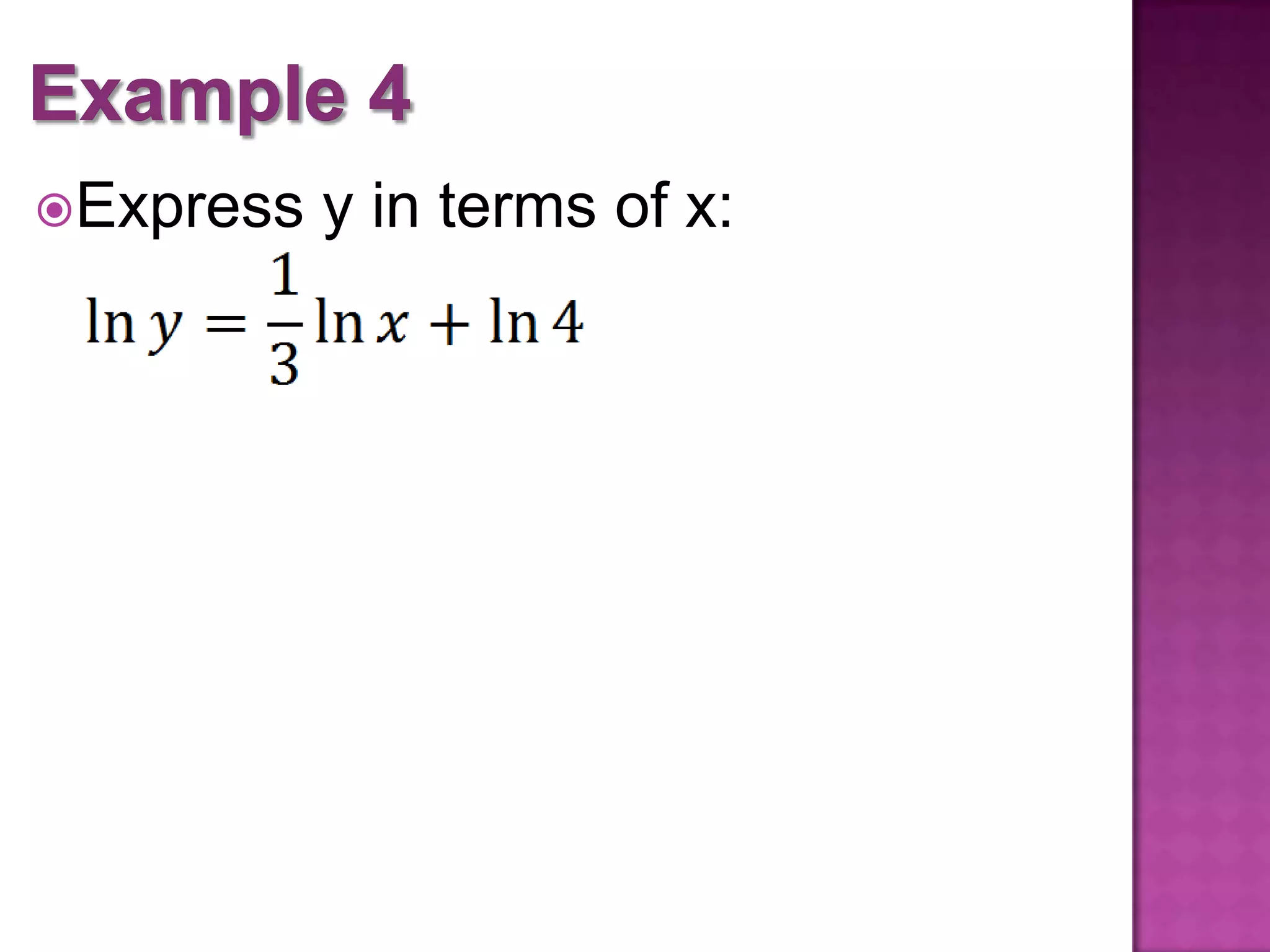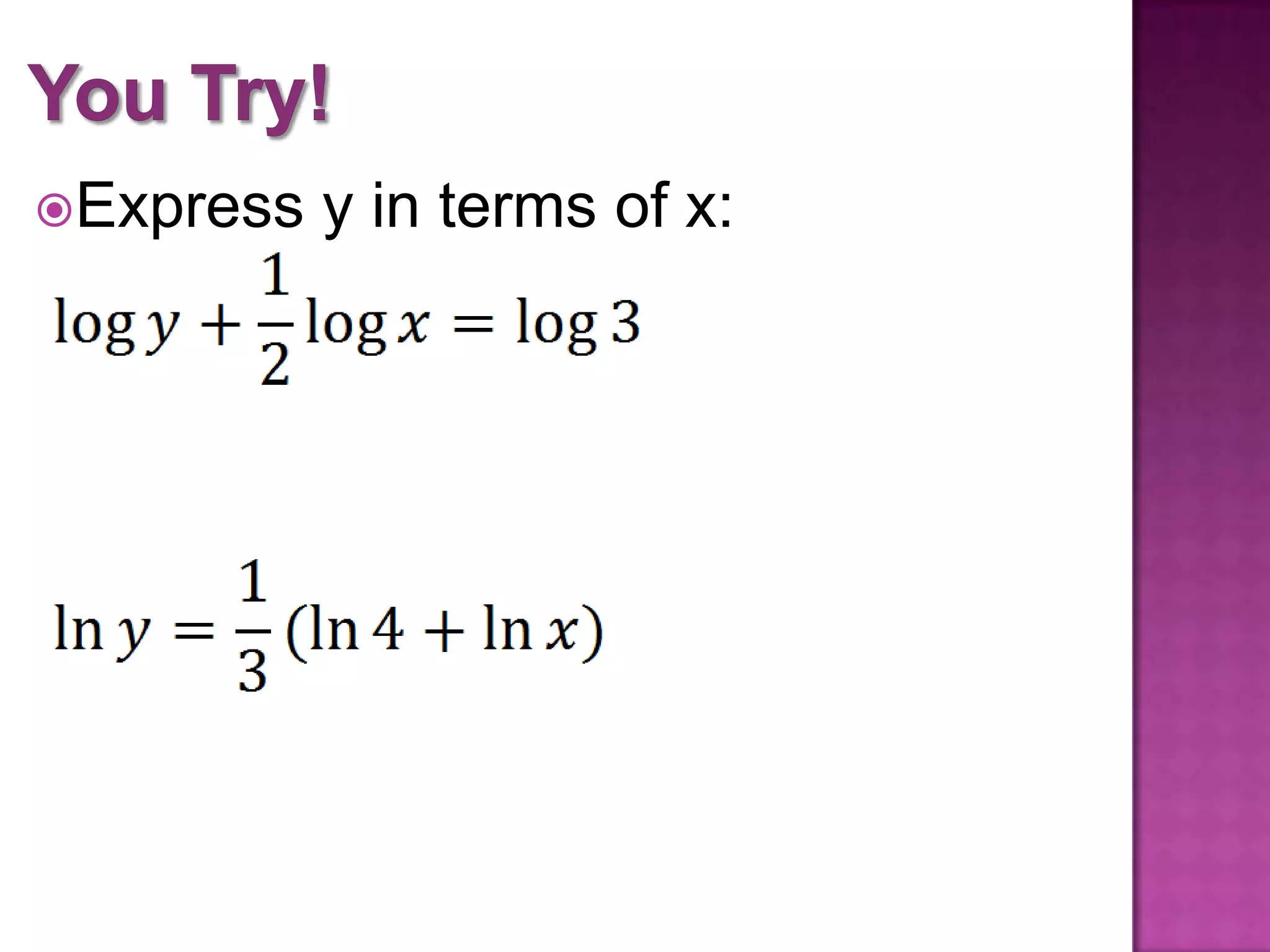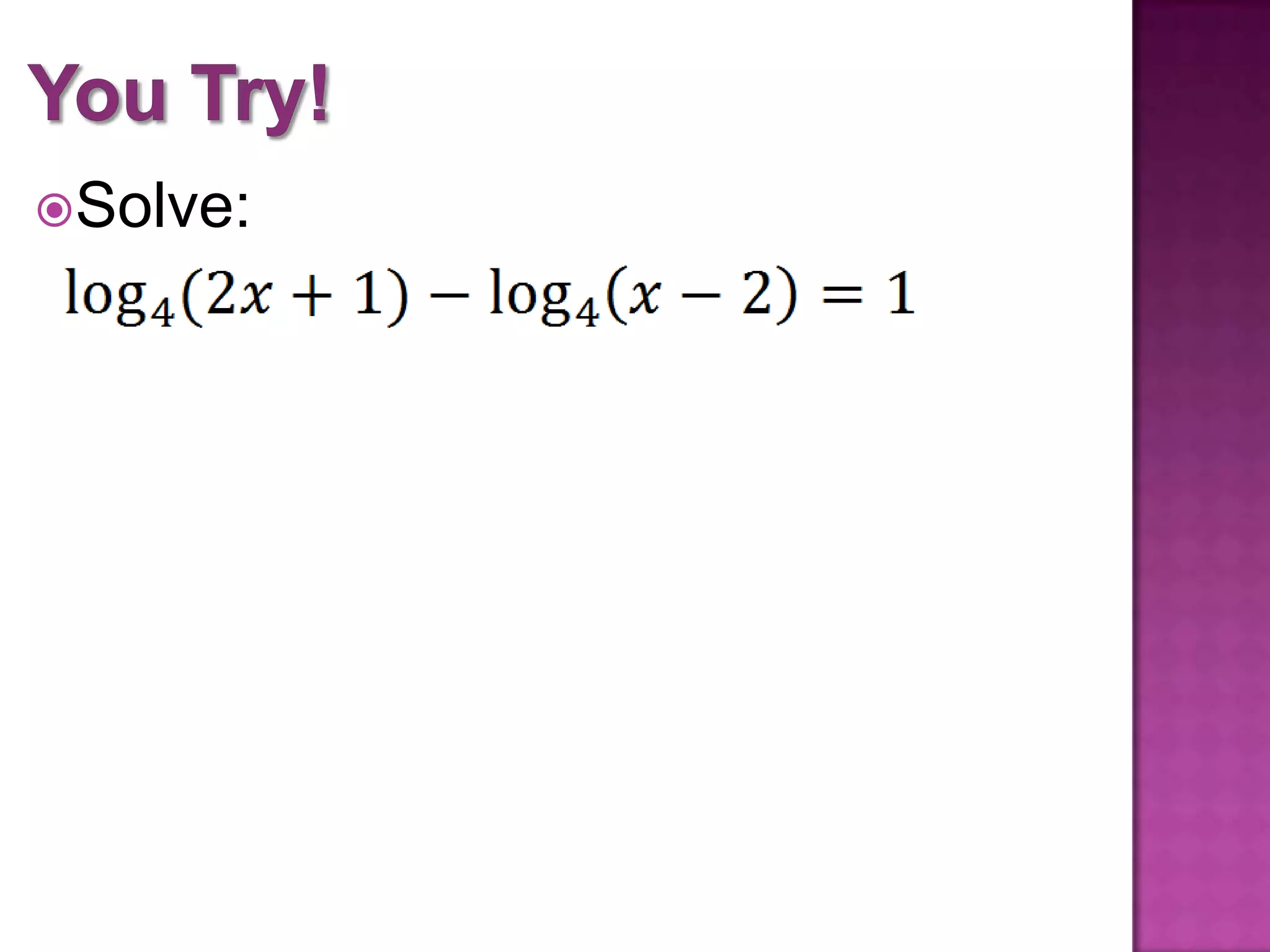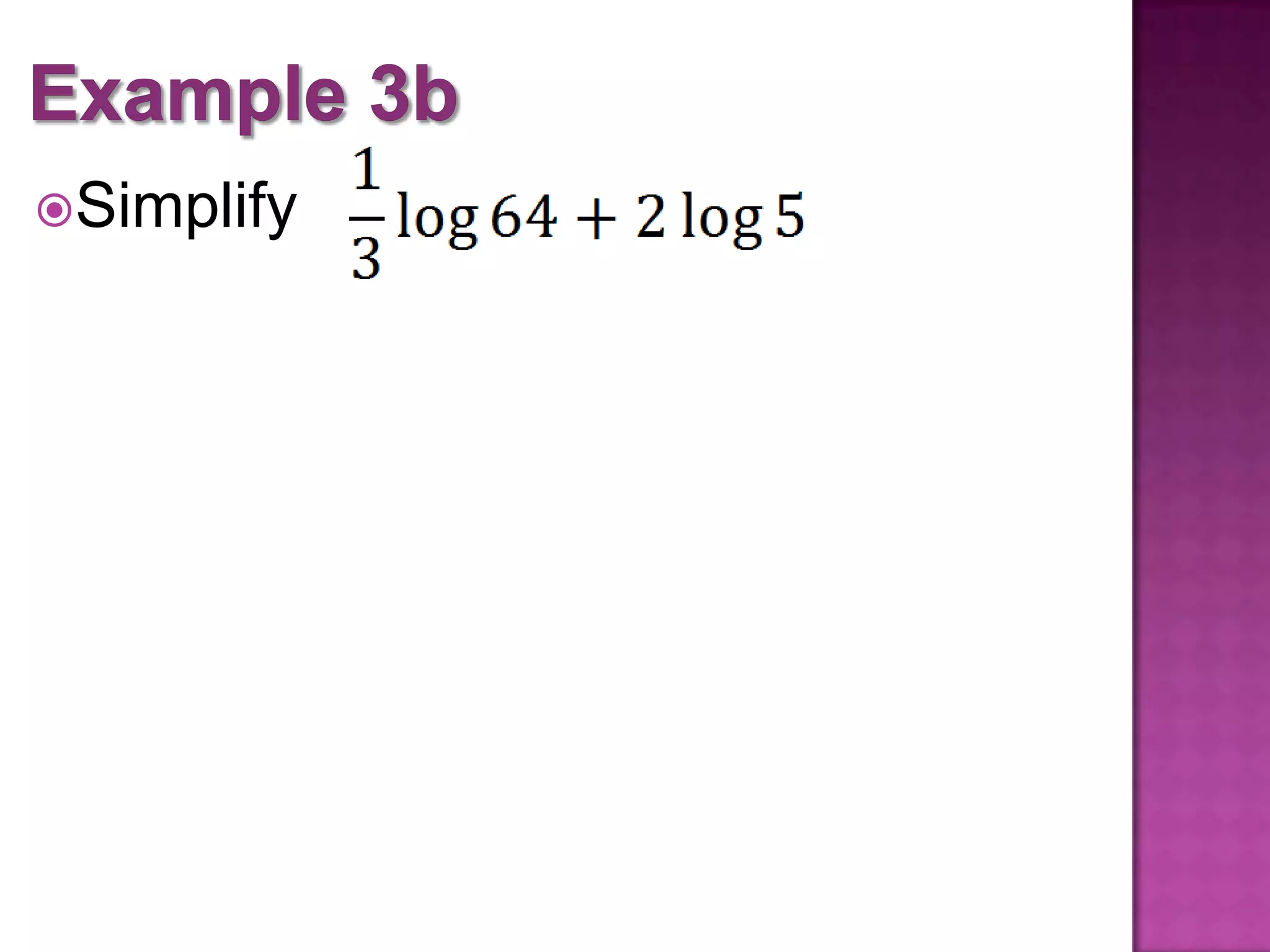
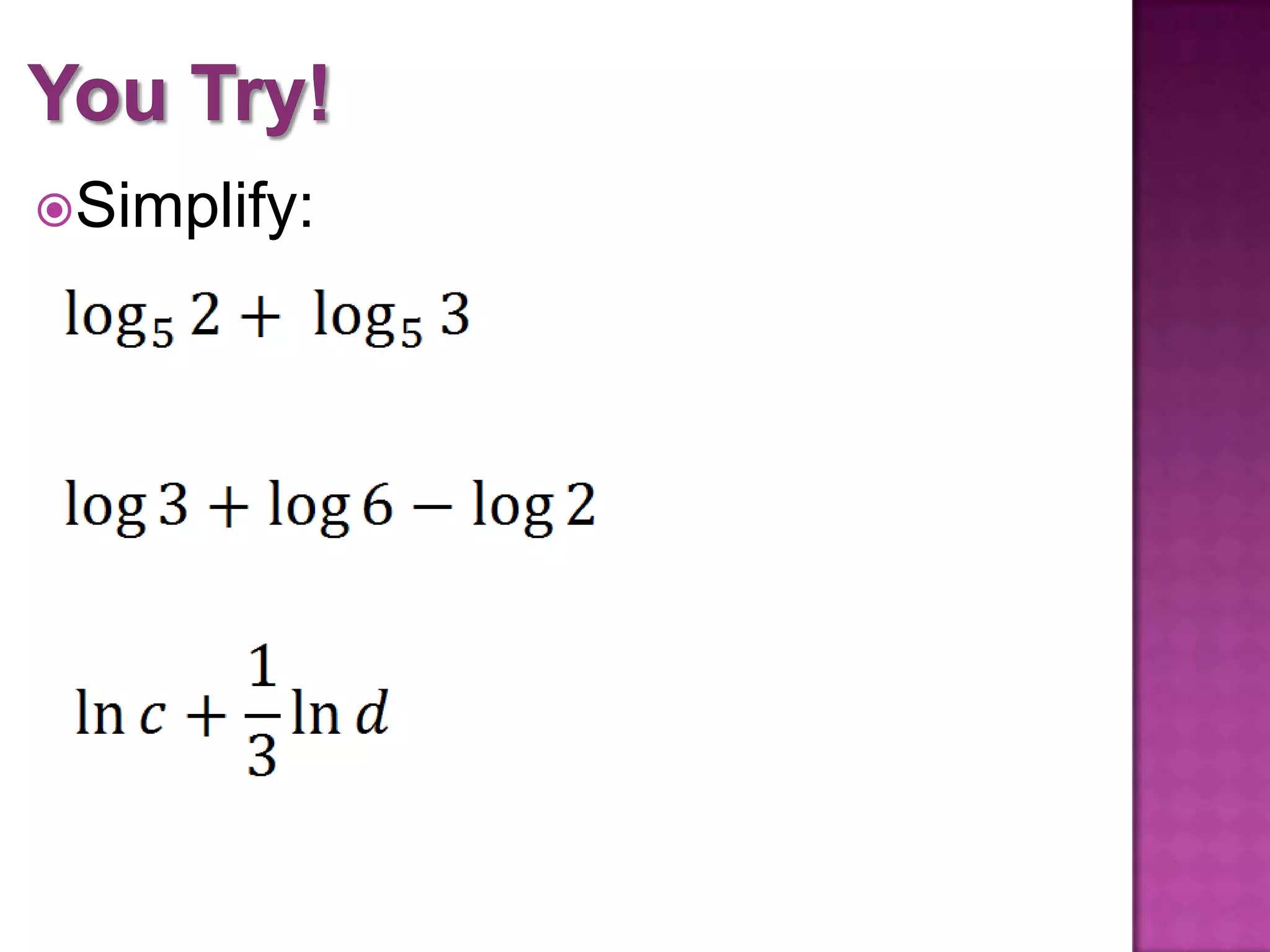
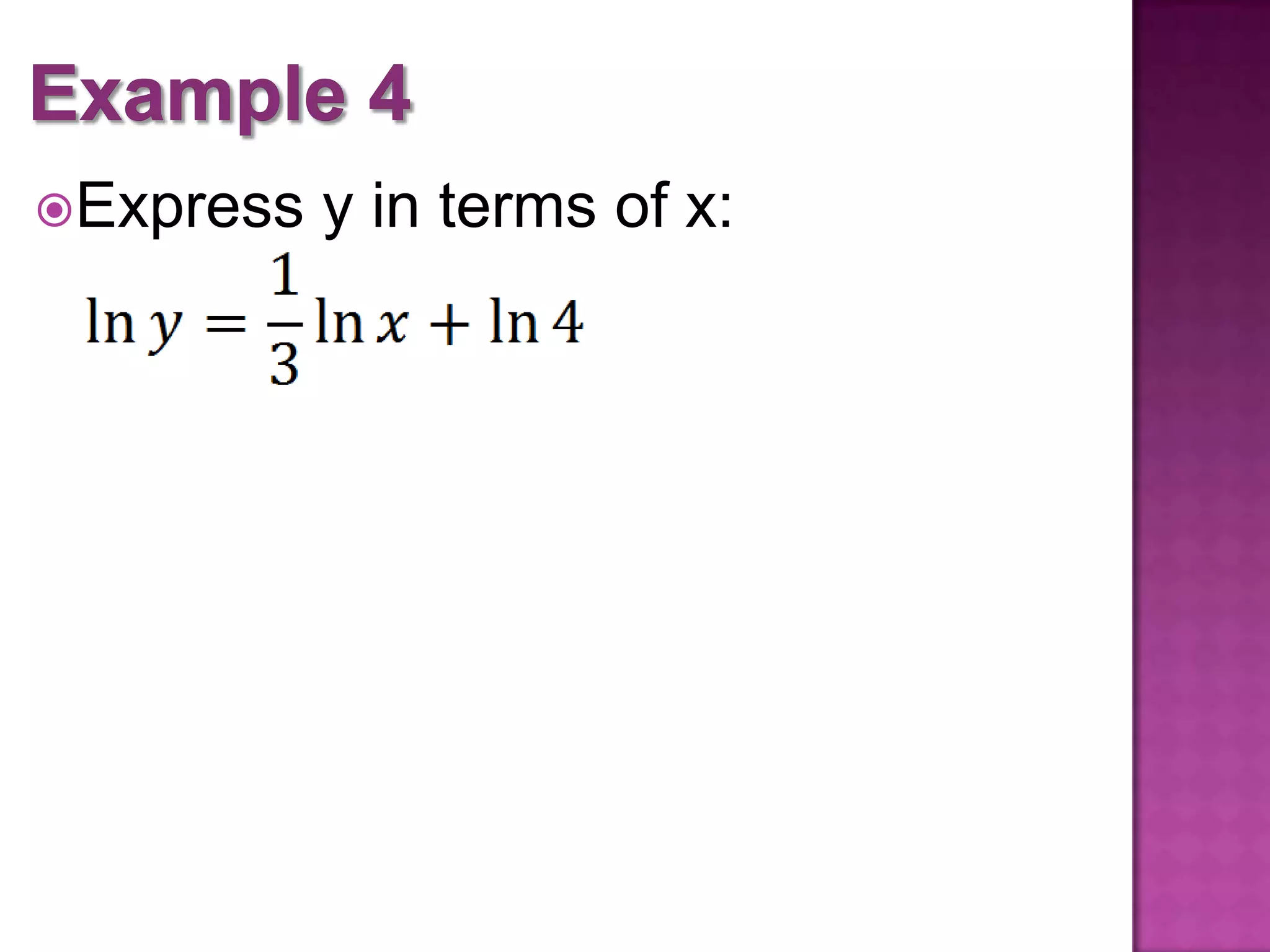
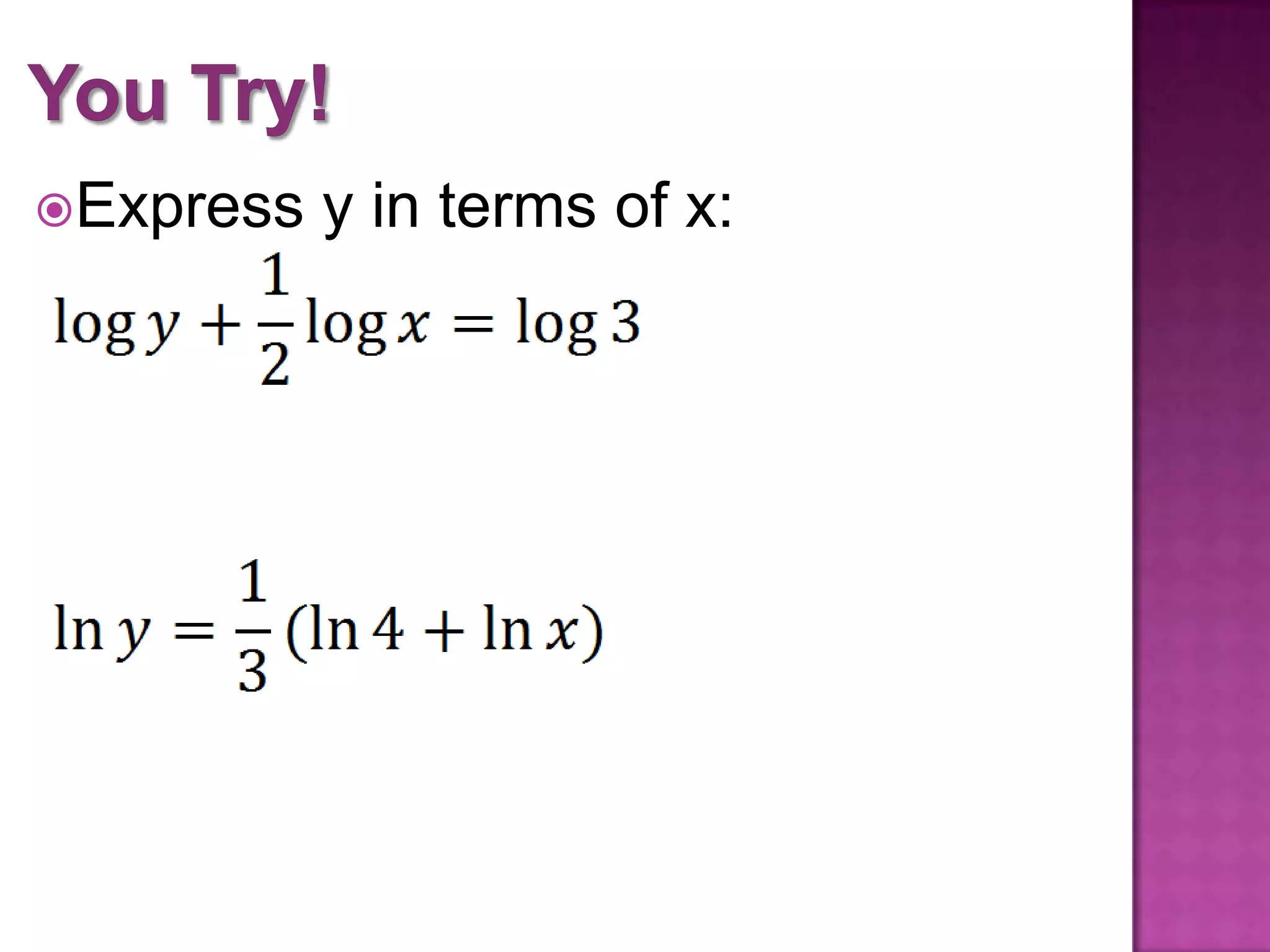
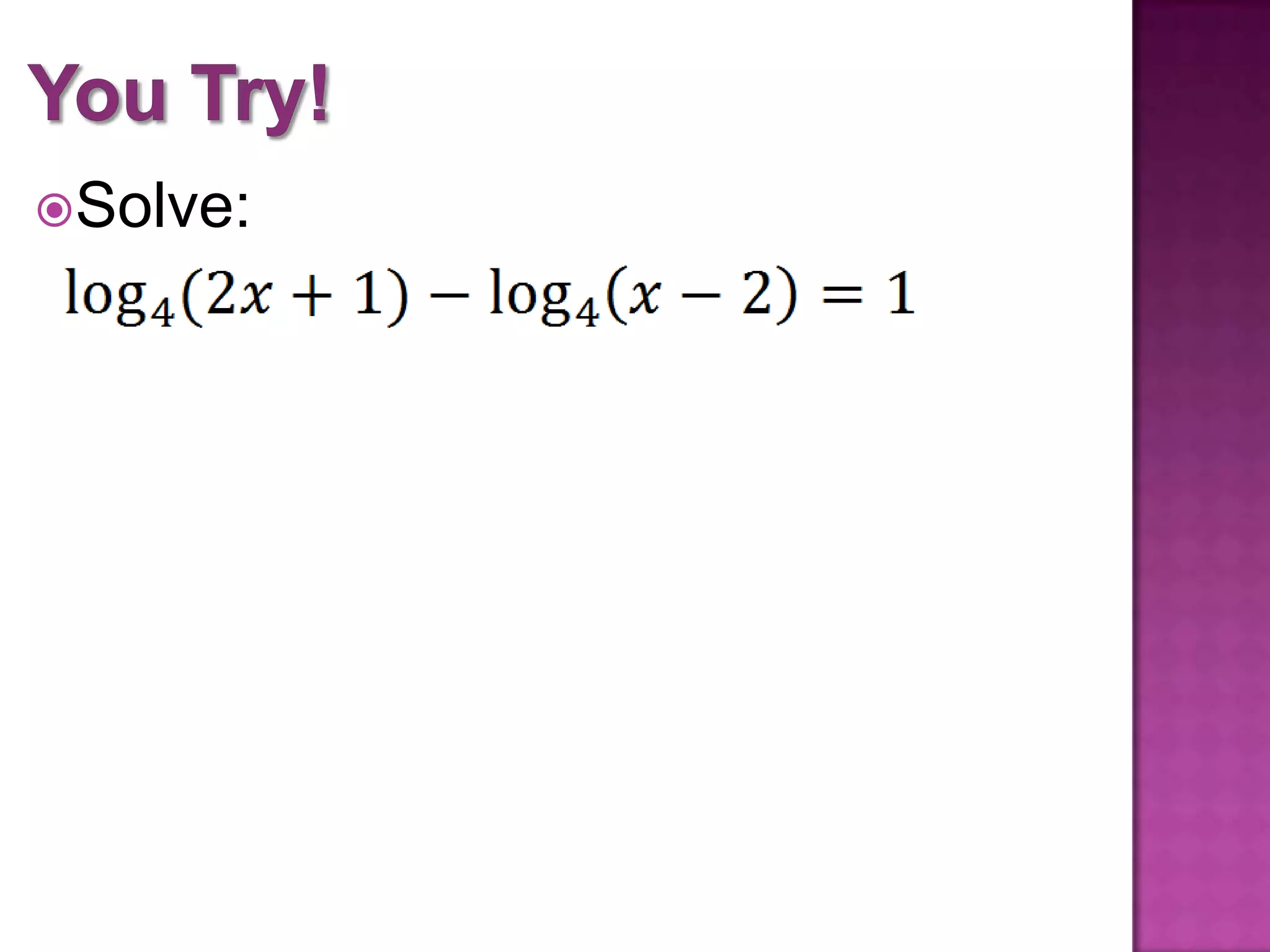
The document outlines objectives and properties for applying laws of logarithms to simplify expressions and solve equations. It defines logarithmic properties, including expressing logarithms in terms of other bases and using the property that logarithmic functions undo each other. It provides examples of simplifying logarithmic expressions and solving logarithmic equations.

1. Objectives:
Apply laws of logarithms to:
•
Simplify expressions
•
Solve equations

2. If
M and N are positive real #s and
b > 0 and ≠ 1, then:

3. Express
in terms of

4. Express
in terms of

5. Express
each in terms of log M
and log N:




6. log 45 – 2 log 3
(express as a single logarithm)
Simplify

7. Simplify

8. Simplify

9. Simplify:

10. If
f(x) = bx then f-1(x) = logb x
Therefore:
f-1(f(x)) = logb bx = x and
f(f-1(x)) = blogb x = x
This
means they “undo” each other.

11. Simplify:

12. Simplify:

13. Express
y in terms of x:

14. Express
y in terms of x:

15. Express
y in terms of x:

16. Solve:

17. Solve:

18. If
log9 5 = x and log9 4 = y, express
in terms of x and y:
log9 100
log9
36

19. If
log9 5 = x and log9 4 = y, express
in terms of x and y:
log9 3.2