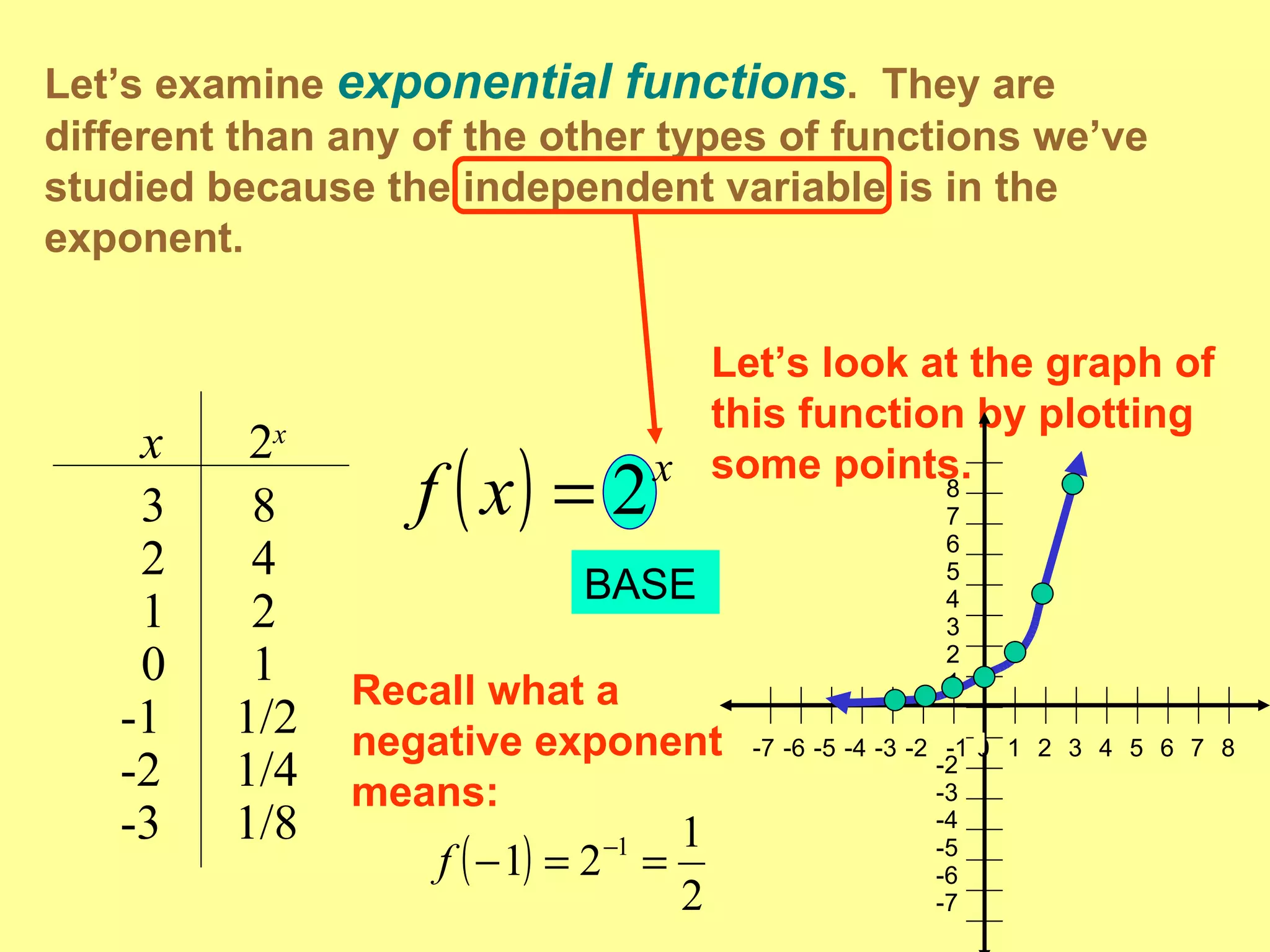
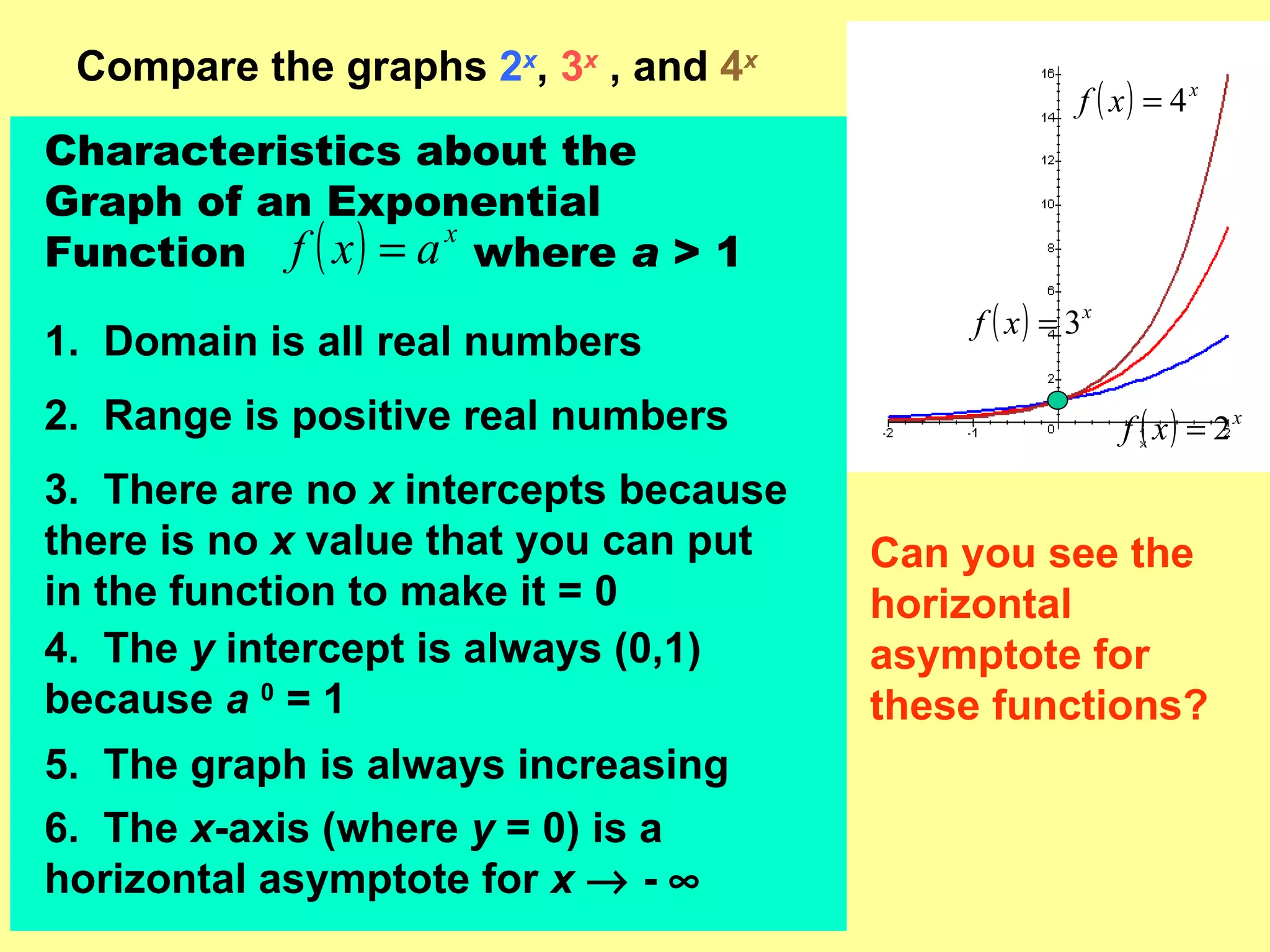
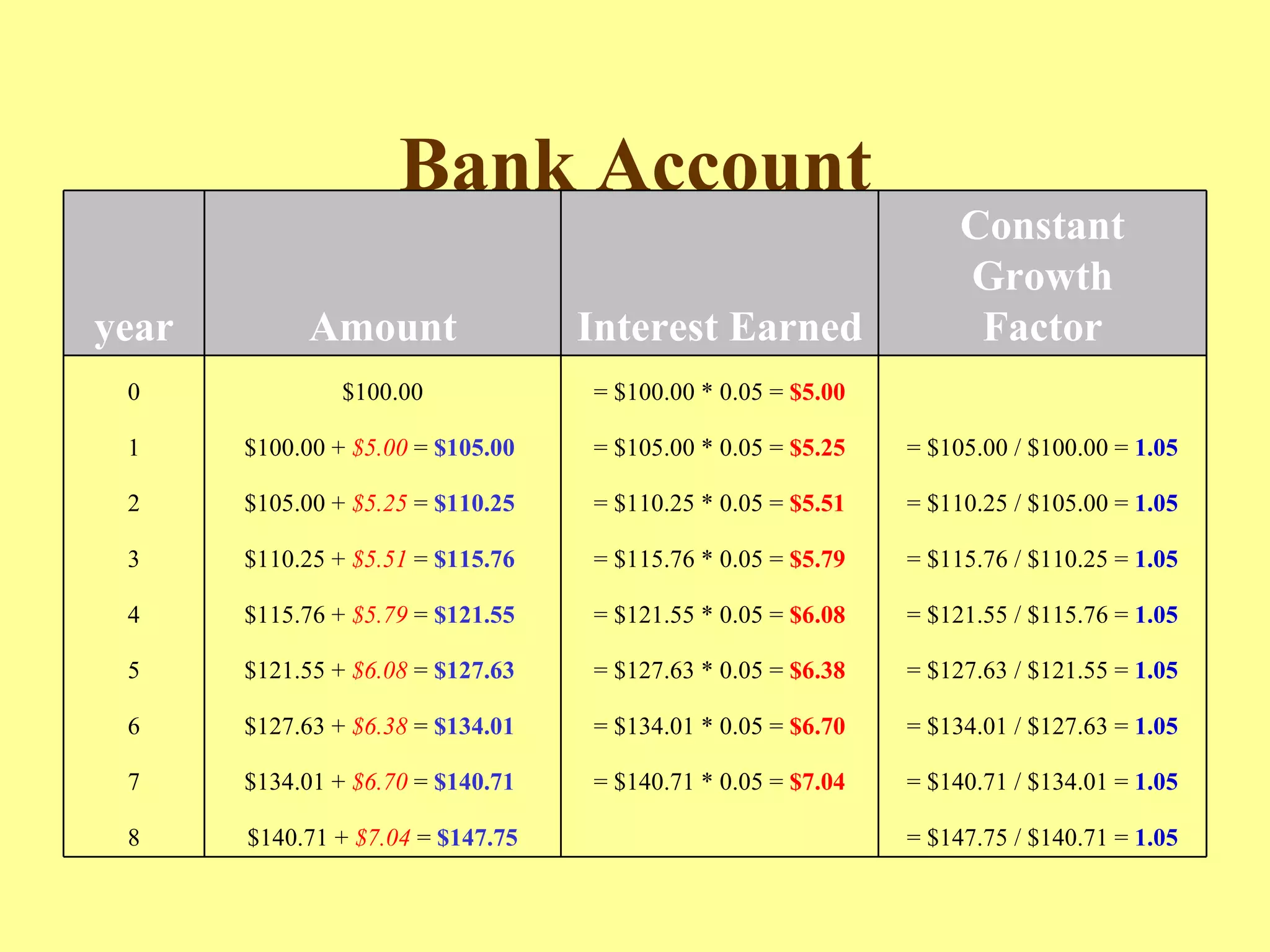
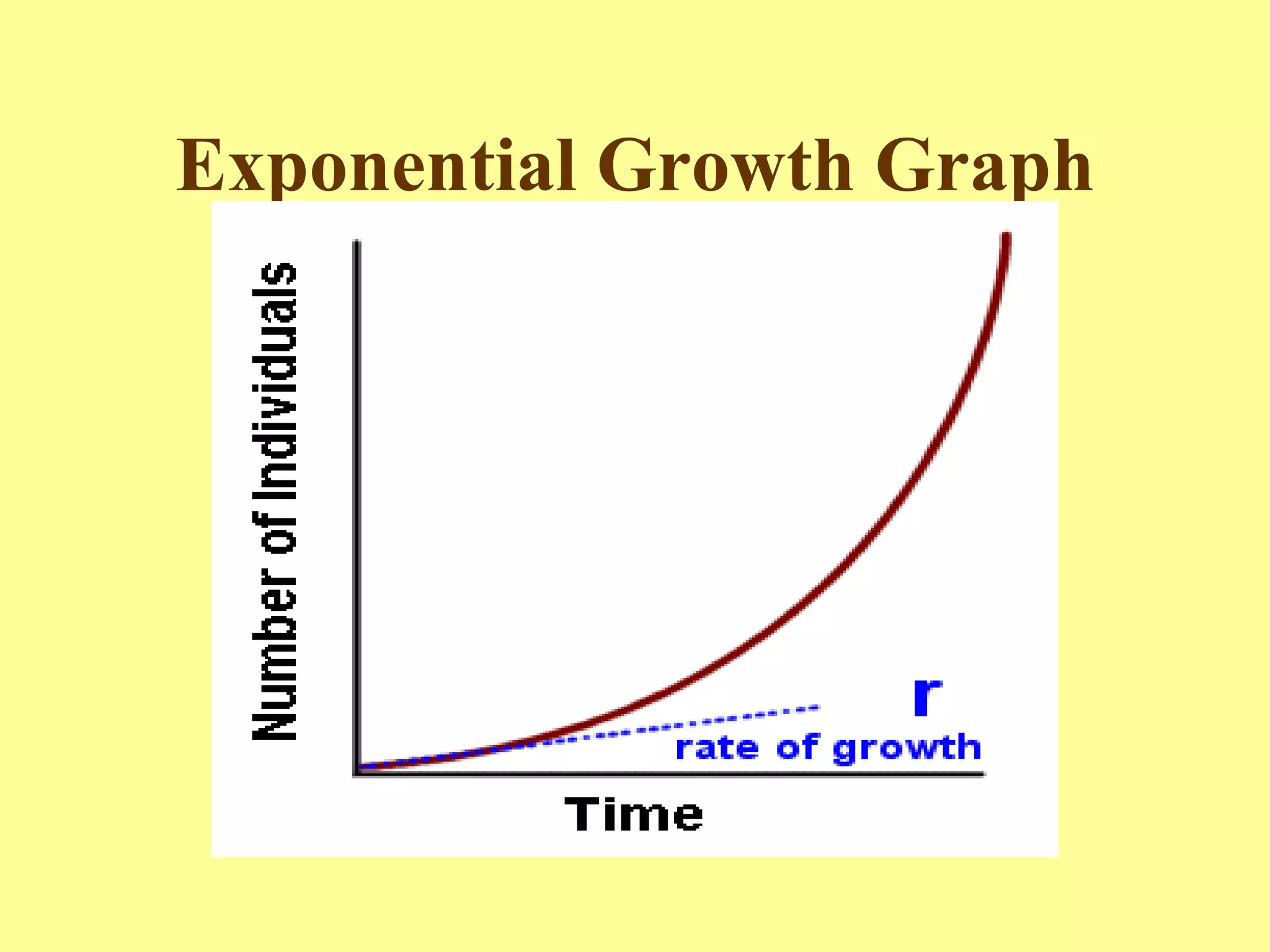
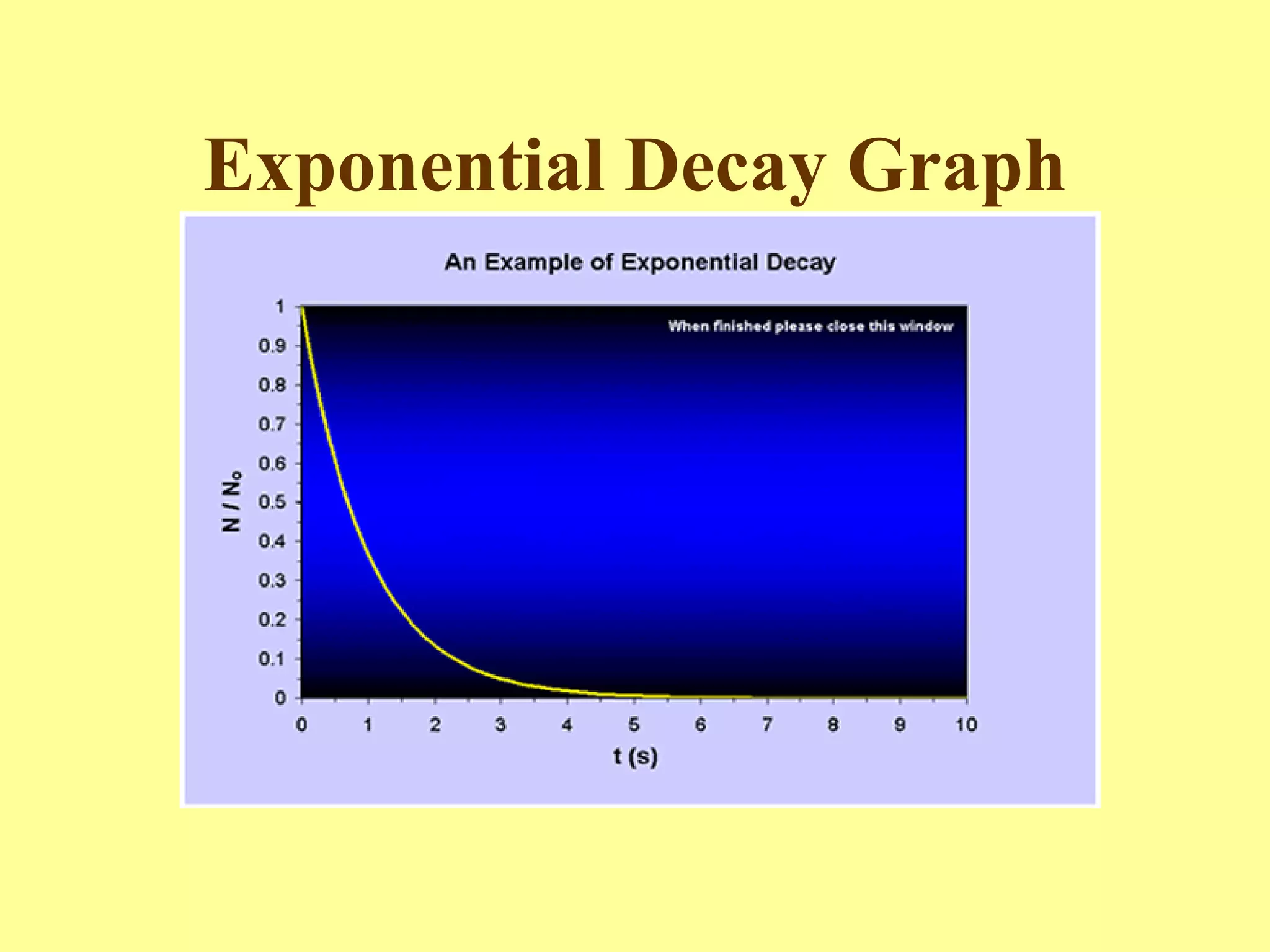
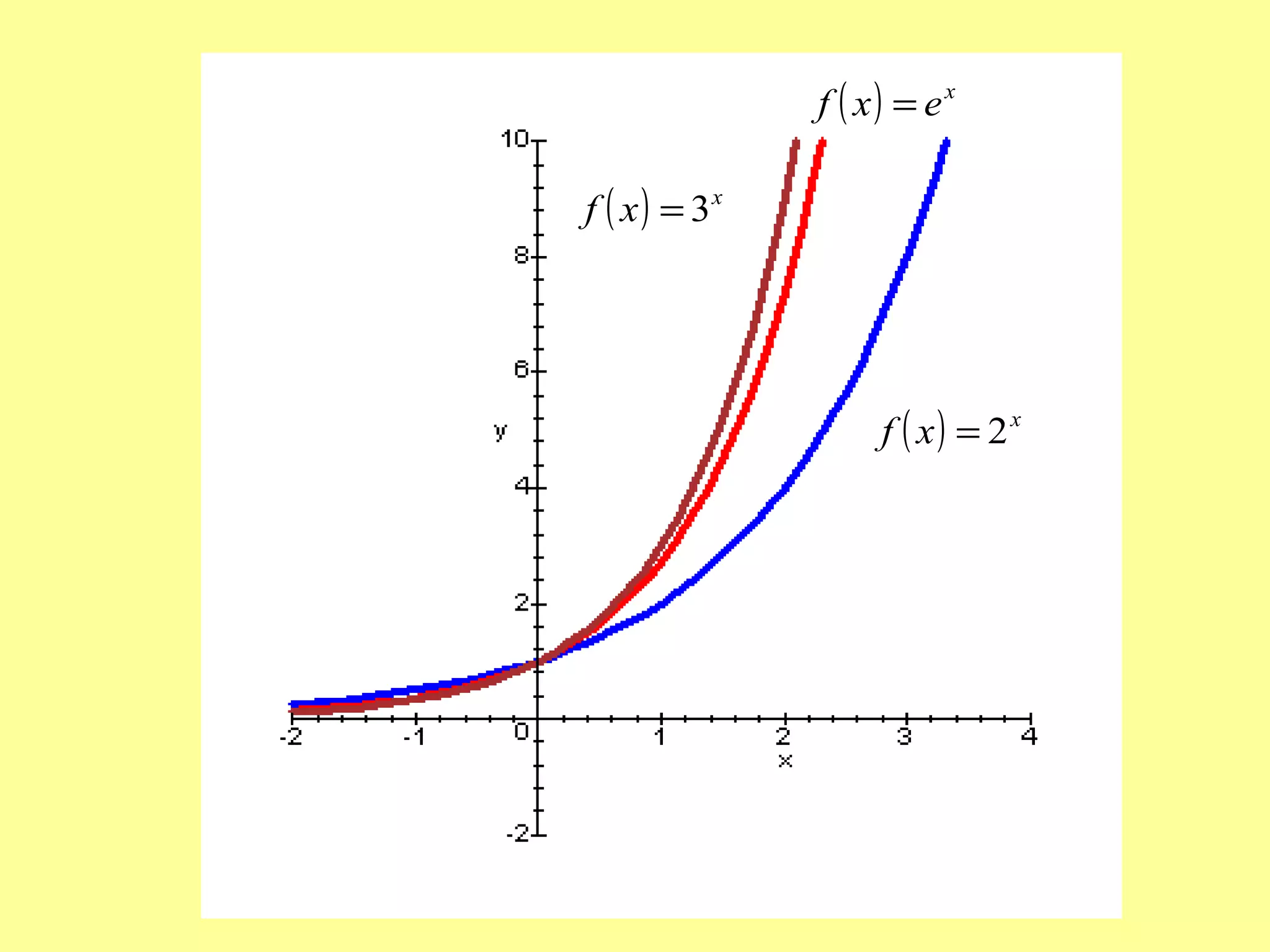
The document discusses exponential functions and their key characteristics: - Exponential functions have a constant growth or decay factor, meaning the dependent variable is multiplied by a fixed amount for each unit change in the independent variable. - When the growth factor is greater than 1, it represents exponential growth. When it is less than 1, it represents exponential decay. - Exponential functions have several distinguishing graphical properties, including having no x-intercepts, a y-intercept of (0,1), and being either always increasing or always decreasing depending on the growth factor.

1. Exponential Functions More Mathematical Modeling

10. Let’s examine exponential functions . They are different than any of the other types of functions we’ve studied because the independent variable is in the exponent. Let’s look at the graph of this function by plotting some points. x 2 x 3 8 2 4 1 2 0 1 -1 1/2 -2 1/4 -3 1/8 Recall what a negative exponent means: BASE 2 -7 -6 -5 -4 -3 -2 -1 1 5 7 3 0 4 6 8 7 1 2 3 4 5 6 8 -2 -3 -4 -5 -6 -7

11. Compare the graphs 2 x , 3 x , and 4 x Characteristics about the Graph of an Exponential Function where a > 1 What is the domain of an exponential function? 1. Domain is all real numbers What is the range of an exponential function? 2. Range is positive real numbers What is the x intercept of these exponential functions? 3. There are no x intercepts because there is no x value that you can put in the function to make it = 0 What is the y intercept of these exponential functions? 4. The y intercept is always (0,1) because a 0 = 1 5. The graph is always increasing Are these exponential functions increasing or decreasing? 6. The x -axis (where y = 0) is a horizontal asymptote for x  -  Can you see the horizontal asymptote for these functions?

12. All of the transformations that you learned apply to all functions, so what would the graph of look like? up 3 up 1 Reflected over x axis down 1 right 2

13. Reflected about y -axis This equation could be rewritten in a different form: So if the base of our exponential function is between 0 and 1 (which will be a fraction), the graph will be decreasing. It will have the same domain, range, intercepts, and asymptote. These two exponential functions have special names.

17. Bank Account = $147.75 / $140.71 = 1.05 $140.71 + $7.04 = $147.75 8 = $140.71 / $134.01 = 1.05 = $140.71 * 0.05 = $7.04 $134.01 + $6.70 = $140.71 7 = $134.01 / $127.63 = 1.05 = $134.01 * 0.05 = $6.70 $127.63 + $6.38 = $134.01 6 = $127.63 / $121.55 = 1.05 = $127.63 * 0.05 = $6.38 $121.55 + $6.08 = $127.63 5 = $121.55 / $115.76 = 1.05 = $121.55 * 0.05 = $6.08 $115.76 + $5.79 = $121.55 4 = $115.76 / $110.25 = 1.05 = $115.76 * 0.05 = $5.79 $110.25 + $5.51 = $115.76 3 = $110.25 / $105.00 = 1.05 = $110.25 * 0.05 = $5.51 $105.00 + $5.25 = $110.25 2 = $105.00 / $100.00 = 1.05 = $105.00 * 0.05 = $5.25 $100.00 + $5.00 = $105.00 1 = $100.00 * 0.05 = $5.00 $100.00 0 Constant Growth Factor Interest Earned Amount year

18. Exponential Growth Graph

23. Exponential Decay Graph

24. Exponential Equations and Inequalities

28. This says that if we have exponential functions in equations and we can write both sides of the equation using the same base, we know the exponents are equal. If a u = a v , then u = v The left hand side is 2 to the something. Can we re-write the right hand side as 2 to the something? Now we use the property above. The bases are both 2 so the exponents must be equal. We did not cancel the 2’s, We just used the property and equated the exponents. You could solve this for x now.

29. Let’s try one more: The left hand side is 4 to the something but the right hand side can’t be written as 4 to the something (using integer exponents) We could however re-write both the left and right hand sides as 2 to the something. So now that each side is written with the same base we know the exponents must be equal. Check:

30. Example 1: (Since the bases are the same we simply set the exponents equal.) Here is another example for you to try: Example 1a:

31. The next problem is what to do when the bases are not the same. Does anyone have an idea how we might approach this?

32. Our strategy here is to rewrite the bases so that they are both the same. Here for example, we know that

33. Example 2: (Let’s solve it now) (our bases are now the same so simply set the exponents equal) Let’s try another one of these.

34. Example 3 Remember a negative exponent is simply another way of writing a fraction The bases are now the same so set the exponents equal.

35. By now you can see that the equality property is actually quite useful in solving these problems. Here are a few more examples for you to try.

37. The Base “ e ” (also called the natural base) To model things in nature, we’ll need a base that turns out to be between 2 and 3. Your calculator knows this base. Ask your calculator to find e 1 . You do this by using the e x button (generally you’ll need to hit the 2nd or yellow button first to get it depending on the calculator). After hitting the e x, you then enter the exponent you want (in this case 1) and push = or enter. If you have a scientific calculator that doesn’t graph you may have to enter the 1 before hitting the e x . You should get 2.718281828 Example for TI-83