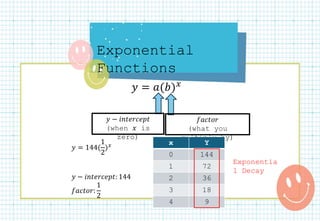
The document covers exponential functions, including their definitions, properties, and examples of exponential growth and decay. It explains the equality property of exponential functions and details how to write exponential functions based on data points, as well as applications such as compound interest formulas. The document also includes examples and exercises related to these concepts.

1. Function
s

2. Objectiv
es
• Define exponential functions
• Evaluate exponential functions
• Use compound interest formulas

3. Properties of
Exponents
• Recall that for a variable 𝑥 and integers 𝑎 and 𝑏:
𝑥𝑎 ∙ 𝑥𝑏 = 𝑥𝑎+𝑏
𝑥𝑎
𝑥𝑏
= 𝑥𝑎−𝑏
(𝑥𝑎)𝑏 = 𝑥𝑎𝑏
𝑥𝑎 𝑏
=
𝑏
𝑥𝑎
𝑥𝑎 = 𝑥𝑏 ⇒ 𝑎 = 𝑏

4. Simplifying
Exponents
Example: Simplify!
1.
25𝑥3𝑦−2𝑧2
5𝑥𝑦2𝑧5
2. (2𝑟2𝑠−3𝑡)4
3. 5𝑦2/3
∙ 6𝑦−1/2

5. Simplifying
Exponents
Example: Simplify!
1.
25𝑥3𝑦−2𝑧2
5𝑥𝑦2𝑧5 = 5𝑥3−1𝑦−2−2𝑧2−5 = 5𝑥2𝑦−4𝑧−3
2. (2𝑟2
𝑠−3
𝑡)4
= 24
𝑟4(2)
𝑠4(−3)
𝑡4
= 16𝑟8
𝑠−12
𝑡4
3. 5𝑦2/3 ∙ 6𝑦−
1
2 = 5 6 𝑦
2
3
−
1
2 = 30 𝑦
1
6

6. Exponential
Functions
• is a function involving exponential expression showing
a relationship between the independent variable 𝑥 and
dependent variable 𝑦 or 𝑓(𝑥).
• It is in form 𝑦 = 𝑎 ∙ 𝑏𝑥
, where 𝑎 ≠ 0, 𝑏 > 0 and 𝑏 ≠
1, and the exponent must be a variable.
• Examples of which are 𝑓 𝑥 = 2𝑥+3 and 𝑦 = 102𝑥

7. Exponential
Functions
𝑦 = 𝑎(𝑏)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡
(when 𝑥 is
zero)
𝑦 = 𝑎(𝑏)0
𝑦 = 𝑎 1
𝑦 = 𝑎
(0, 𝑎)

8. Exponential
Functions
𝑦 = 𝑎(𝑏)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡
(when 𝑥 is
zero)
𝑦 = 5(2)𝑥
𝑓𝑎𝑐𝑡𝑜𝑟
(what you
multiply by)
x Y
0 5
1 10
2 20
3 40
4 80

9. Exponential
Functions
𝑦 = 𝑎(𝑏)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡
(when 𝑥 is
zero)
𝑦 = 3(2)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡:
𝑓𝑎𝑐𝑡𝑜𝑟:
𝑓𝑎𝑐𝑡𝑜𝑟
(what you
multiply by)

10. Exponential
Functions
𝑦 = 𝑎(𝑏)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡
(when 𝑥 is
zero)
𝑦 = 3(2)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡: 3
𝑓𝑎𝑐𝑡𝑜𝑟: 2
𝑓𝑎𝑐𝑡𝑜𝑟
(what you
multiply by)

11. Exponential
Functions
𝑦 = 𝑎(𝑏)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡
(when 𝑥 is
zero)
𝑦 = 3(2)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡: 3
𝑓𝑎𝑐𝑡𝑜𝑟: 2
𝑓𝑎𝑐𝑡𝑜𝑟
(what you
multiply by)
x Y
0
1
2
3
4

12. Exponential
Functions
𝑦 = 𝑎(𝑏)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡
(when 𝑥 is
zero)
𝑦 = 3(2)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡: 3
𝑓𝑎𝑐𝑡𝑜𝑟: 2
𝑓𝑎𝑐𝑡𝑜𝑟
(what you
multiply by)
x Y
0 3
1 6
2 12
3 24
4 48

13. Exponential
Functions
𝑦 = 𝑎(𝑏)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡
(when 𝑥 is
zero)
𝑦 = 3(2)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡: 3
𝑓𝑎𝑐𝑡𝑜𝑟: 2
𝑓𝑎𝑐𝑡𝑜𝑟
(what you
multiply by)
x Y
0 3
1 6
2 12
3 24
4 48
Exponentia
l Growth

14. Exponential
Functions
𝑦 = 𝑎(𝑏)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡
(when 𝑥 is
zero)
𝑦 = 144(
1
2
)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡:
𝑓𝑎𝑐𝑡𝑜𝑟:
𝑓𝑎𝑐𝑡𝑜𝑟
(what you
multiply by)

15. Exponential
Functions
𝑦 = 𝑎(𝑏)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡
(when 𝑥 is
zero)
𝑦 = 144(
1
2
)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡: 144
𝑓𝑎𝑐𝑡𝑜𝑟:
1
2
𝑓𝑎𝑐𝑡𝑜𝑟
(what you
multiply by)

16. Exponential
Functions
𝑦 = 𝑎(𝑏)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡
(when 𝑥 is
zero)
𝑦 = 144(
1
2
)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡: 144
𝑓𝑎𝑐𝑡𝑜𝑟:
1
2
𝑓𝑎𝑐𝑡𝑜𝑟
(what you
multiply by)
x Y
0
1
2
3
4

17. Exponential
Functions
𝑦 = 𝑎(𝑏)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡
(when 𝑥 is
zero)
𝑦 = 144(
1
2
)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡: 144
𝑓𝑎𝑐𝑡𝑜𝑟:
1
2
𝑓𝑎𝑐𝑡𝑜𝑟
(what you
multiply by)
x Y
0 144
1 72
2 36
3 18
4 9

18. Exponential
Functions
𝑦 = 𝑎(𝑏)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡
(when 𝑥 is
zero)
𝑦 = 144(
1
2
)𝑥
𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡: 144
𝑓𝑎𝑐𝑡𝑜𝑟:
1
2
𝑓𝑎𝑐𝑡𝑜𝑟
(what you
multiply by)
x Y
0 144
1 72
2 36
3 18
4 9
Exponentia
l Decay

19. Exponential
Functions
The graph of an exponential function is called an
exponential curve.
Exponential
Growth
Exponential
Decay
Factor (b) is greater
than 1.
𝒃 > 𝟏
Factor (b) is between
0 and 1.
𝟎 < 𝒃 < 𝟏

20. Exponential
Functions
Determine whether each function shows exponential
growth or exponential decay.
1. 𝑓 𝑥 = 3(5)𝑥 2. 𝑓 𝑥 = 6(
2
3
)𝑥
3. 𝑓 𝑥 = 3(0.25)𝑥 4. 𝑓 𝑥 = 3(1.37)𝑥

21. Exponential
Functions
Determine whether each function shows exponential
growth or exponential decay.
1. 𝑓 𝑥 = 3(5)𝑥 2. 𝑓 𝑥 = 6(
2
3
)𝑥
The factor (b) is greater than 1.
Exponential Growth
3. 𝑓 𝑥 = 3(0.25)𝑥 4. 𝑓 𝑥 = 3(1.37)𝑥

22. Exponential
Functions
Determine whether each function shows exponential
growth or exponential decay.
1. 𝑓 𝑥 = 3(5)𝑥 2. 𝑓 𝑥 = 6(
2
3
)𝑥
The factor (b) is greater than 1. The factor (b) is between 0 and 1
Exponential Growth Exponential Decay
3. 𝑓 𝑥 = 3(0.25)𝑥 4. 𝑓 𝑥 = 3(1.37)𝑥

23. Exponential
Functions
Determine whether each function shows exponential
growth or exponential decay.
1. 𝑓 𝑥 = 3(5)𝑥 2. 𝑓 𝑥 = 6(
2
3
)𝑥
The factor (b) is greater than 1. The factor (b) is between 0 and 1
Exponential Growth Exponential Decay
3. 𝑓 𝑥 = 3(0.25)𝑥 4. 𝑓 𝑥 = 3(1.37)𝑥
The factor (b) is between 0 and 1.
Exponential Decay

24. Exponential
Functions
Determine whether each function shows exponential
growth or exponential decay.
1. 𝑓 𝑥 = 3(5)𝑥 2. 𝑓 𝑥 = 6(
2
3
)𝑥
The factor (b) is greater than 1. The factor (b) is between 0 and 1
Exponential Growth Exponential Decay
3. 𝑓 𝑥 = 3(0.25)𝑥 4. 𝑓 𝑥 = 3(1.37)𝑥
The factor (b) is between 0 and 1. The factor (b) is greater than 1.
Exponential Decay Exponential Growth

25. The Equality
Property of
Exponential
Functions
We know that in exponential functions, the exponent is a
variable. When we wish to solve for that variable, we have
two approaches we can take. One approach is to use a
logarithm. The second is to make use of the Equality
Property for Exponential Functions.

26. The Equality
Property of
Exponential
Functions
Suppose 𝑏 is a positive number other than 1. Then 𝑏𝑥1 =
𝑏𝑥2 if and only if 𝑥1 = 𝑥2.

27. The Equality
Property of
Exponential
Functions
Example 1:
32𝑥−5 = 3𝑥+3 (Since the bases are the same, we simply set the exponents equal).
2𝑥 − 5 = 𝑥 + 3
𝑥 − 5 = 3
𝑥 = 8

28. The Equality
Property of
Exponential
Functions
Let’s try!
23𝑥−1 = 2
1
3
𝑥+5

29. The Equality
Property of
Exponential
Functions
Let’s try!
23𝑥−1 = 2
1
3
𝑥+5
3𝑥 − 1 = 1/3𝑥 + 5
𝑥 =
9
4
or 2.25

30. The Equality
Property of
Exponential
Functions
Example 2: (When the bases are not the same)
32𝑥+3 = 27𝑥−1
33 = 27
Rewrite the bases so that
they are the same.

31. The Equality
Property of
Exponential
Functions
Example 2: (When the bases are not the same)
32𝑥+3 = 27𝑥−1
32𝑥+3
= 33(𝑥−1)
2𝑥 + 3 = 3𝑥 − 3
−𝑥 = −6
𝑥 = 6
The bases are now the
same.

32. The Equality
Property of
Exponential
Functions
Let’s Try!
16𝑥+1 =
1
32

33. The Equality
Property of
Exponential
Functions
Let’s Try!
16𝑥+1 =
1
32
24(𝑥+1) = 2−5
4𝑥 + 4 = −5
𝑥 = −
9
4

34. Exponential
Growth or Decay
• A function that models exponential growth grows by a rate proportional to
the amount present. For any real number 𝑥 and any positive real numbers 𝑎
and 𝑏 such that 𝑏 ≠ 1, an exponential growth function has the form 𝑓 𝑥 =
𝑎𝑏𝑥
where
𝑎 is the initial or starting value of the function
𝑏 is the growth factor or growth multiplier per unit 𝑥

35. Writing
Exponential
Functions
• Given two data points, how do we write an exponential model?
1. If one of the data points has the form (0, 𝑎)(the 𝑦 − 𝑖𝑛𝑡𝑒𝑟𝑐𝑒𝑝𝑡), then 𝑎 is
the initial value. Substitute 𝑎 into the equation 𝑦 = 𝑎(𝑏)𝑥, and solve for 𝑏
with the second set of values.
2. Otherwise, substitute both points into two equations with the form and solve
the system.
3. Using 𝑎 and 𝑏 found in the steps 1 or 2, write the exponential function in
the form 𝑓 𝑥 = 𝑎(𝑏)𝑥.

36. Writing
Exponential
Functions
Example:
In 2006, 80 deer were introduced into a wildlife refuge. By 2012, the population
had growth to 180 deer. The population was growing exponentially. Write an
exponential function 𝑁(𝑡) representing the population (𝑁) of deer over time 𝑡.

37. Writing
Exponential
Functions
Example:
In 2006, 80 deer were introduced into a wildlife refuge. By 2012, the population
had growth to 180 deer. The population was growing exponentially. Write an
exponential function 𝑁(𝑡) representing the population (𝑁) of deer over time 𝑡.
If we let 𝑡 be the number of years after 2006, we can write the information in the
problem as two ordered pairs: (0,80) and (6,180). We also have an initial value,
so 𝑎 = 80, and we can use the process in step 1.

38. Writing
Exponential
Functions
Set up the initial equation (𝑦 = 𝑎(𝑏)𝑥) and substitute 𝑎 and the second set of
values into it.
180 = 80(𝑏)6
𝑏6 =
180
80
=
9
4
𝑏 = (
9
4
)
1
6≈ 1.1447
Thus, the function becomes 𝑁 𝑡 = 80(1.447)𝑡

39. Writing
Exponential
Functions
Example: Find an exponential function that passes through the points (-2,6) and
(2,1).
Since we don’t have an initial value, we will need to set up and solve a system.
It will usually be simplest to use the first equation with the first set of values for
𝑎, and then substitute that into the second equation with the second set of values
to solve for 𝑏.

40. Writing
Exponential
Functions
Example: Find an exponential function that passes through the points (-2,6) and
(2,1).
6 = 𝑎𝑏−2 1 = (6𝑏2)𝑏2 𝑎 = 6(0.6389)2
6 =
𝑎
𝑏2 1 = 6𝑏4
= 2.4492
𝑎 = 6𝑏2
𝑏4
=
1
6
𝑏 =
1
6
1
4
≈ 0.6389
Thus, the function is 𝑓 𝑥 = 2.4492(0.6389)𝑥

41. Compound
Interest
• The formula for compound interest (interest paid on both principal and
interest) is an important application of exponential functions.
• Recall that the formula for simple interest, 𝐼 = 𝑃𝑟𝑡, where 𝑃 is principal
(amount deposited), 𝑟 is annual rate of interest, and 𝑡 is time in years.

42. Compound
Interest
• Now, suppose we deposit $1000 at 10% annual interest. At the end of the
first year, we have
𝐼 = 1000 0.1 = 100
so our account now has 1000 + .1(1000) = $1100.
• At the end of the second year, we have
𝐼 = 1100 .1 = 110
so our account now has 1100 + .1(1100) = $1210.

43. Compound
Interest
• Another way to write 1000 + .1(1000) is
1000(1 + .1)
• After the second year, this gives us
1000 (1 + .1) + .1(1000(1 + .1)) = 1000 (1 + .1)(1 + .1)
= 1000 (1 + .1)2

44. Compound
Interest
• If we continue, we end up with
This leads us to the general formula.
Year Account
1 $1100 1000(1 + .1)
2 $1210 1000(1 + .1)2
3 $1331 1000(1 + .1)3
4 $1464.10 1000(1 + .1)4
𝑡 1000(1 + .1)𝑡

45. Compound
Interest
Formulas
• For interest compounded 𝑛 times per year:
𝐴 = 𝑃(1 +
𝑟
𝑛
)𝑡𝑛
• For interest compounded continuously:
𝐴 = 𝑃𝑒𝑟𝑡
where 𝑒 is the irrational constant 2.718281 …

46. Compound
Interest
Formulas
Example:
1. If $2500 is deposited in an account paying 6% per year compounded twice
per year, how much is the account worth after 10 years with no
withdrawals?
𝐴 = 2500(1 +
.06
2
)2(10) 𝑃 = 2500, 𝑟 = .06,
𝑛 = 2, 𝑡 = 10
𝐴 = 2500(1 +
.06
2
)2 10 = $4515.28

47. Compound
Interest
Formulas
Example:
2. What amount deposited today at 4.8% compounded quarterly will give
$15,000 in 8 years?
15000 = 𝑃(1 +
.048
4
)4 8 A = 15000, 𝑟 = .048,
𝑛 = 4, 𝑡 = 8

48. Compound
Interest
Formulas
Example:
2. What amount deposited today at 4.8% compounded quarterly will give
$15,000 in 8 years?
15000 = 𝑃(1 +
.048
4
)4 8
15000 ≈ 𝑃(1.4648)
P = $10,240.35

50. Individual Task
A. Using the Equality Property of Exponential Functions, determine
the value of 𝑥.
1. 32𝑥−1 = 1
9
2. 4𝑥+3 = 82𝑥+1
B. Solve.
3. Which is a better deal, depositing $7000 at 6.25% compounded
every month for 5 years or 5.75% compounded continuously for 6
years?