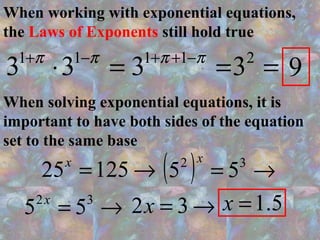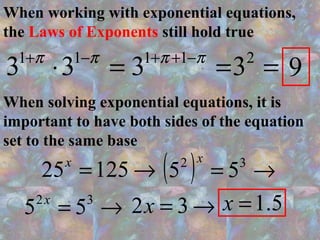
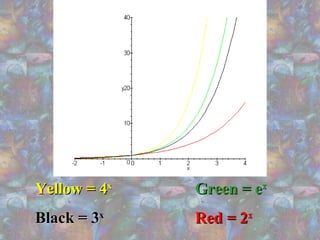
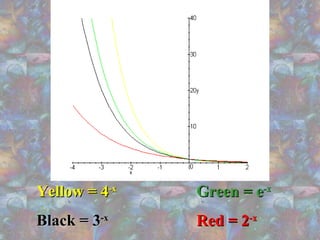
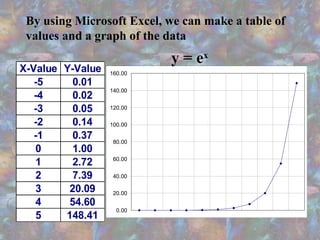
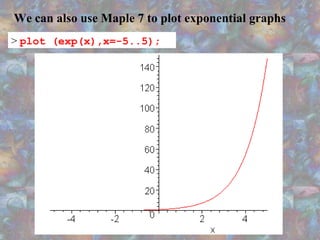
The document discusses exponential functions, highlighting their common characteristics and equations in the form y = ab^x. It explains the importance of having both sides of an exponential equation set to the same base and provides examples of how different bases affect the graph's growth rate. Additionally, it mentions the use of Microsoft Excel and Maple 7 for plotting exponential graphs and illustrates the concept of exponential growth in real life.

1. • 100’s of free ppt’s from
www.pptpoint.com library

2. Exponential
Functions are
functions which
can be
represented by
graphs similar
to the graph on
the right

3. All base exponential functions are similar because
they all go through the point (0,1), regardless of
the size of their base number
Exponential Functions are written in the form:
y = abx
a= constant b = base x = variable

4. When solving exponential equations, it is
important to have both sides of the equation
set to the same base
When working with exponential equations,
the Laws of Exponents still hold true
=⋅ −+ ππ 11
33 =−++ ππ 11
3 =2
3 9
→=12525x
( ) →= 32
55
x
→= 32
55 x
→= 32x 5.1=x

5. Yellow = 4Yellow = 4xx
Green = eGreen = exx
Black = 3Black = 3xx
Red = 2Red = 2xx

6. As you could see in the graph, the larger the
base, the faster the function increased
If we place a negative sign in front of the x,
the graphs will be reflected(flipped) across
the y-axis

7. Yellow = 4Yellow = 4-x-x
Green = eGreen = e-x-x
Black = 3Black = 3-x-x
Red = 2Red = 2-x-x

8. X-Value Y-Value
-5 0.01
-4 0.02
-3 0.05
-2 0.14
-1 0.37
0 1.00
1 2.72
2 7.39
3 20.09
4 54.60
5 148.41
0.00
20.00
40.00
60.00
80.00
100.00
120.00
140.00
160.00
By using Microsoft Excel, we can make a table of
values and a graph of the data
y = ex

9. We can also use Maple 7 to plot exponential graphs
> plot (exp(x),x=-5..5);

10. The previous pages show what exponential growth
looks like as a curve, but what happens in real life.
You start with one item which replicates continuously.

11. Homework:
Pages ?