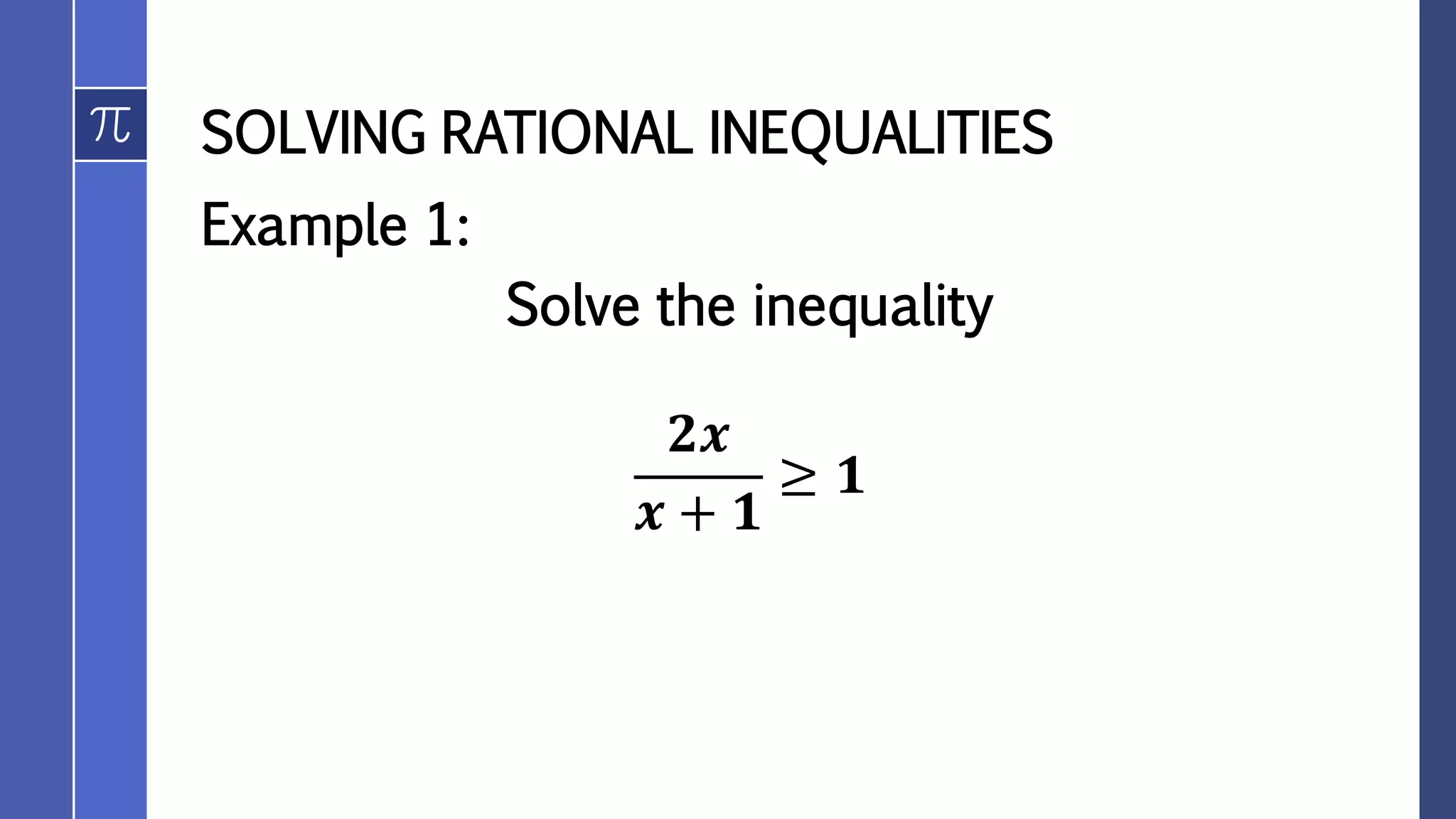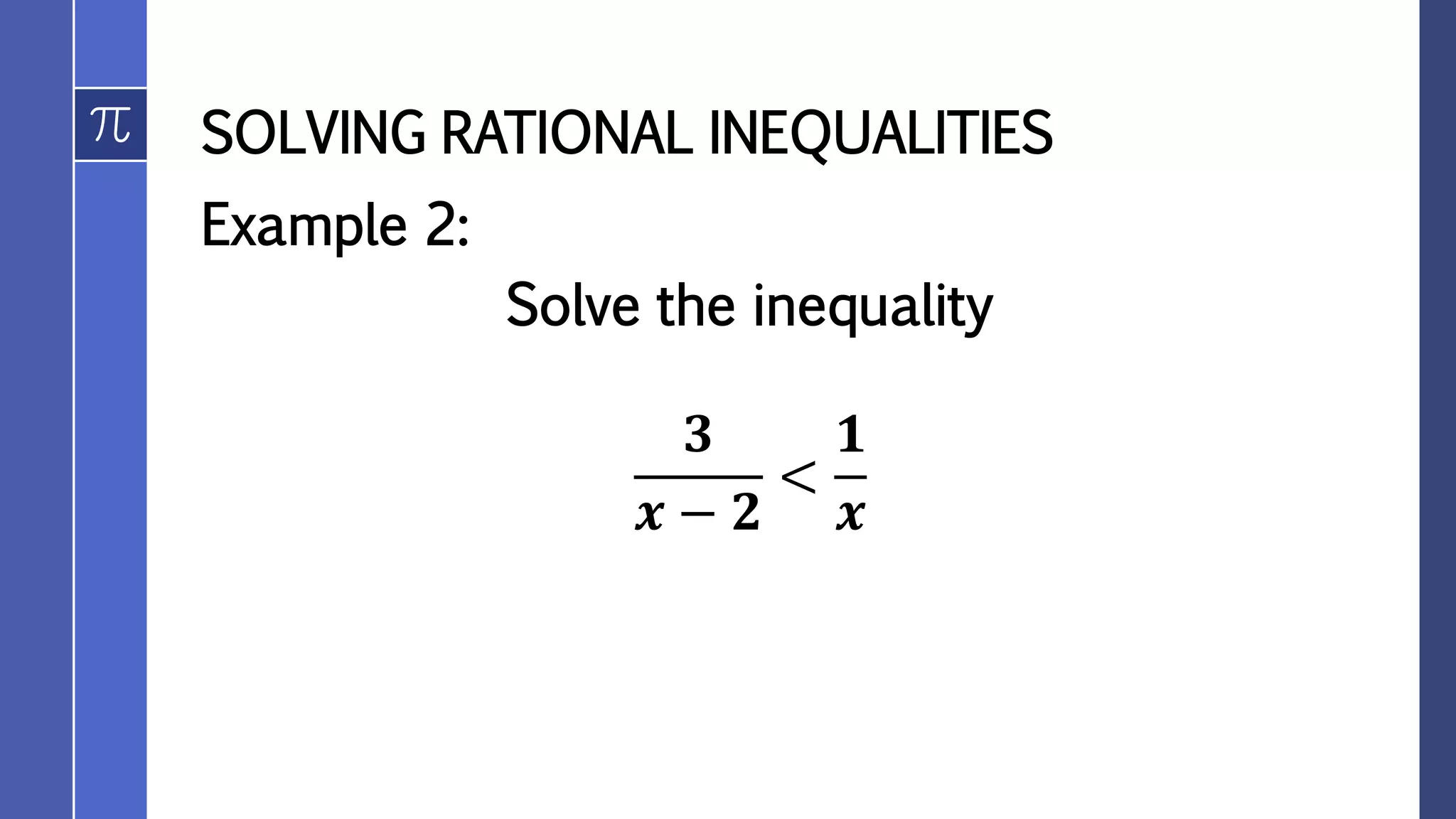The document discusses solving rational inequalities. It defines interval and set notation that can be used to represent the solutions to inequalities. It then presents the procedure for solving rational inequalities, which involves rewriting the inequality as a single fraction on one side of the inequality symbol and 0 on the other side, and determining the intervals where the fraction is positive or negative. Examples are provided to demonstrate solving rational inequalities and applying the solutions to word problems.

1. SOLVING RATIONAL
INEQUALITIES
www.slideshare.net/reycastro1
General Mathematics

2. RATIONAL INEQUALITIES
› LEARNING OUTCOMES:
› Able to solve rational inequalities and solve
problems involving rational inequalities.

3. INTERVAL AND SET NOTATION
An inequality may have infinitely many
solutions. The set of all solutions can be
expressed using set notation or interval
notation.

4. INTERVAL AND SET NOTATION

5. INTERVAL AND SET NOTATION
Ex. If -2 < x < 2
Interval: (-2, 2)
Set Notation: { x|-2 < x < 2 }

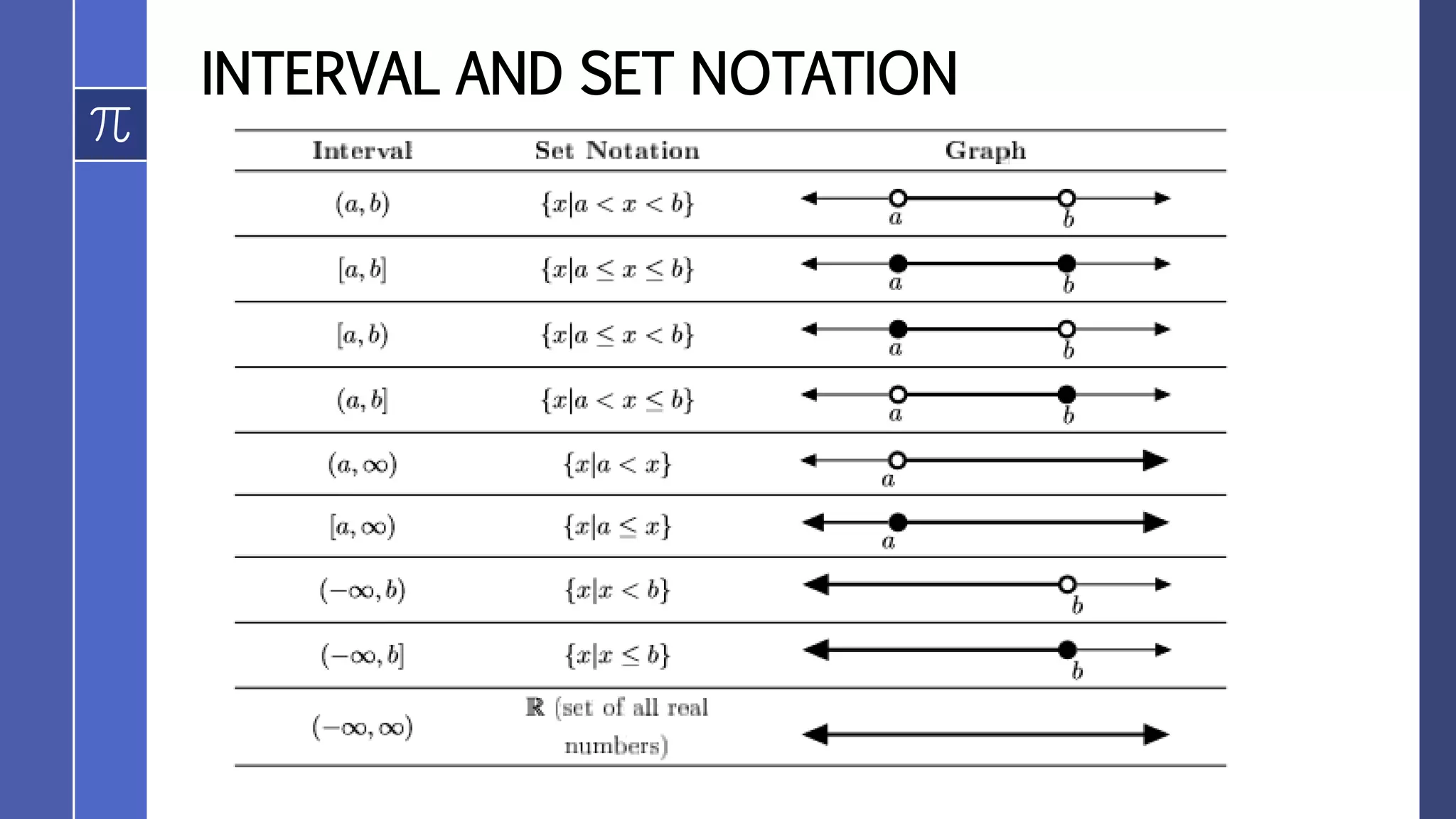
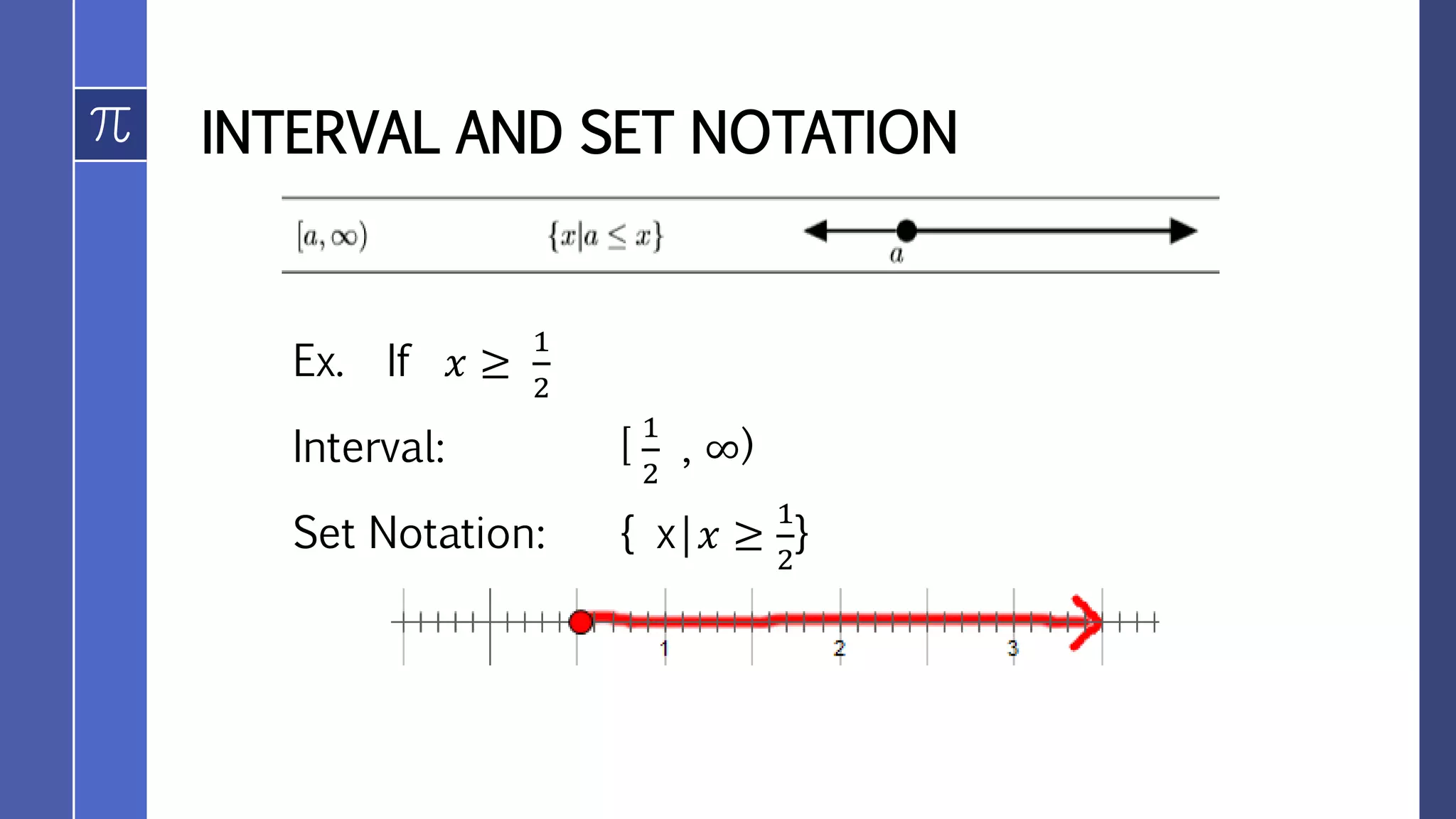
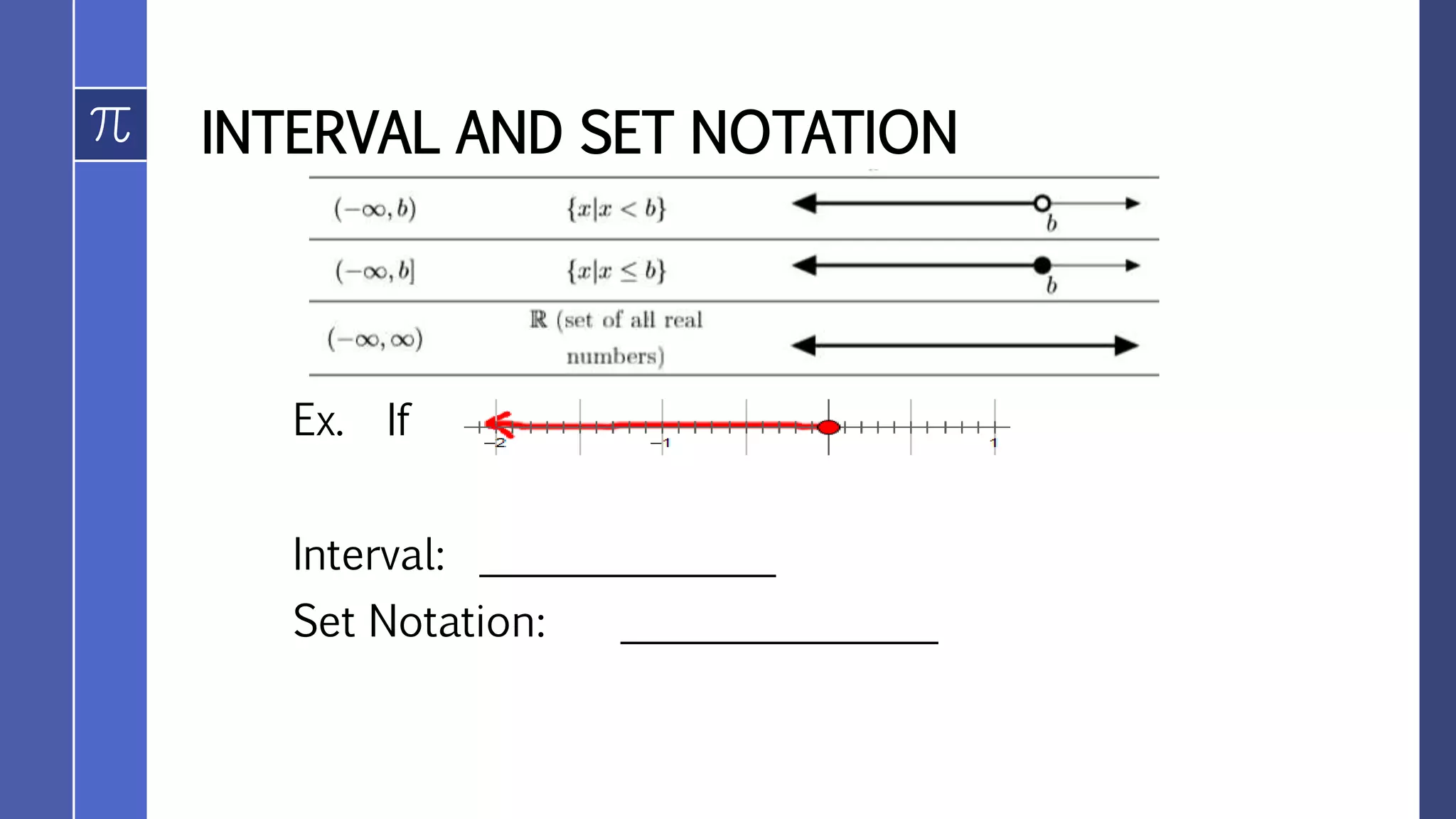
6. INTERVAL AND SET NOTATION
Ex. If 0 ≤ 𝑥 ≤ 3
Interval: [0, 3]
Set Notation: { x| 0 ≤ 𝑥 ≤ 3 }

7. INTERVAL AND SET NOTATION
Ex. If −1 ≤ 𝑥 < 2 and 0.5 < 𝑥 ≤ 4
Interval: ________ and __________
Set Notation: ______ and __________
Graph:

8. INTERVAL AND SET NOTATION
Ex. If 𝑥 > −2
Interval: (-2, ∞)
Set Notation: { x|𝑥 > -2 }

9. INTERVAL AND SET NOTATION
Ex. If 𝑥 ≥
1
2
Interval: [
1
2
, ∞)
Set Notation: { x|𝑥 ≥
1
2
}

10. INTERVAL AND SET NOTATION
Ex. If
Interval: ______________
Set Notation: _______________

11. INTERVAL AND SET NOTATION
Ex. If x < -1
Interval: ______________
Set Notation: _______________
Graph:

12. PROCEDURE FOR SOLVING RATIONAL
INEQUALITIES
To solve rational inequalities
a. Rewrite the inequality as a single
fraction on one side of the inequality
symbol and 0 on the other side.
b. Determine over what intervals the
fraction takes on positive and negative
values.

13. SOLVING RATIONAL INEQUALITIES
Example 1:
Solve the inequality
𝟐𝒙
𝒙 + 𝟏
≥ 𝟏

14. SOLVING RATIONAL INEQUALITIES
Example 1: Solve the inequality
𝟐𝒙
𝒙 + 𝟏
≥ 𝟏
The solution set is 𝒙 ∈ ℝ|𝒙 < −𝟏 𝒐𝒓 𝒙 ≥ 𝟏
The interval notation: −∞, −𝟏 ∪ 𝟏, ∞)

15. SOLVING RATIONAL INEQUALITIES
Example 2:
Solve the inequality
𝟑
𝒙 − 𝟐
<
𝟏
𝒙

16. SOLVING RATIONAL INEQUALITIES
Example 3:
A box with a square base is to have a
volume of 8 cubic meters. Let x be the
length of the side of the square base and h
be the height of the box. What are the
possible measurements of a side of the
square base if the height should be longer
than a side of the square base?

17. SOLVING RATIONAL INEQUALITIES
Example 4: A dressmaker ordered several meters
of red cloth from a vendor only but 4 meters of
red cloth in stock. The vendor bought the
remaining lengths of red cloth from a wholesaler
for P1120. He then sold those lengths of red cloth
to the dressmaker along with the original 4
meters of cloth for a total of P1600. if the
vendor’s price per meter is at least P10 more than
the wholesaler’s price per meter, what possible
lengths of cloth did the vendor purchase from the
wholesaler?

18. Try this!
Find the solutions of the following.
(a)
3
𝑥+1
=
2
𝑥−3
(b)
𝑥+1
𝑥+3
≤ 2
(c) You have a 6 liters of a pineapple juice blend
that is 50% pineapple juice. How many liters of pure
pineapple juice needs to be added to make a juice
blend that is 75% pineapple juice?
Hint: If x is the amount of pure pineapple juice to be
added, the percentage can be written as
3+𝑥
6+𝑥

19. THANK YOU
www.slideshare.net/reycastro1
@reylkastro2
reylkastro