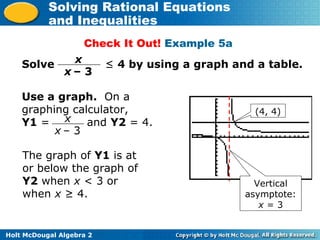
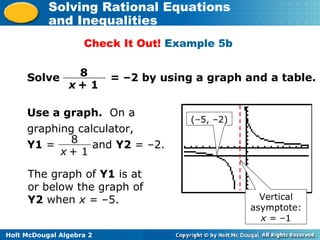
This document discusses solving rational equations and inequalities. It begins with definitions of rational equations and inequalities. Examples are provided to demonstrate how to solve rational equations by multiplying both sides by the least common denominator to eliminate fractions. The document notes that extraneous solutions may arise and must be checked. Methods for solving rational inequalities using graphs, tables, and algebra are presented. Practice problems are included for students to test their understanding.