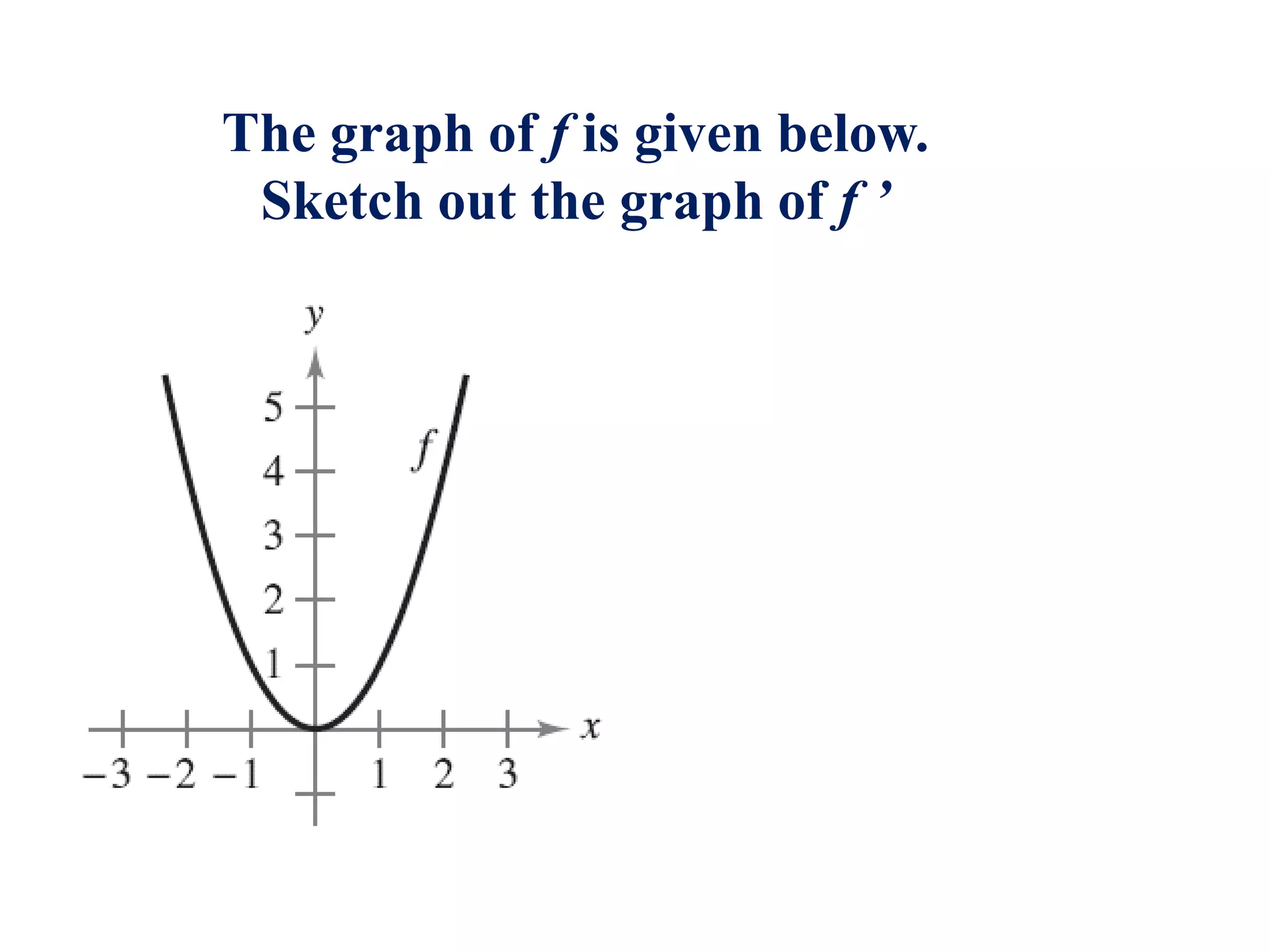
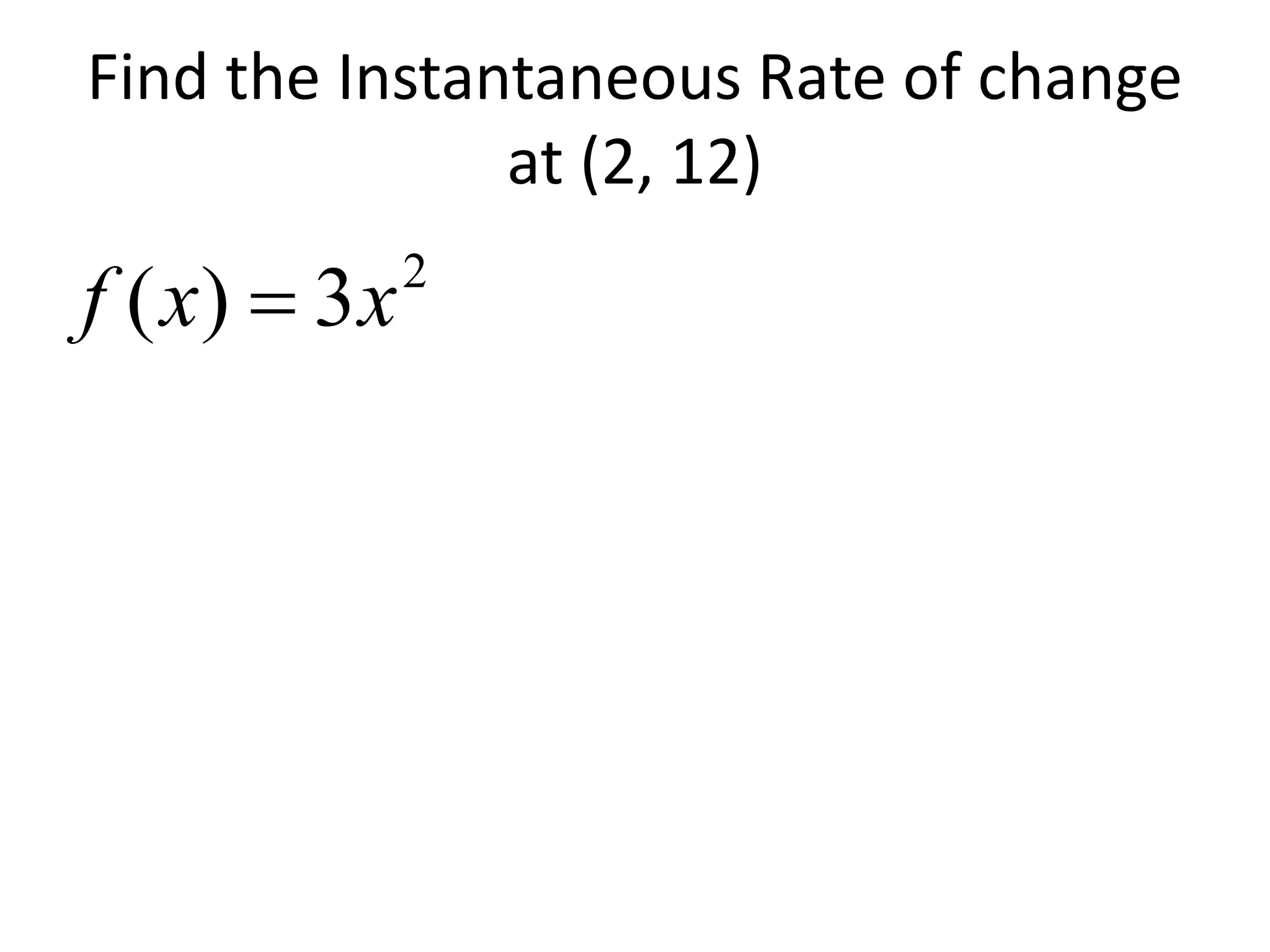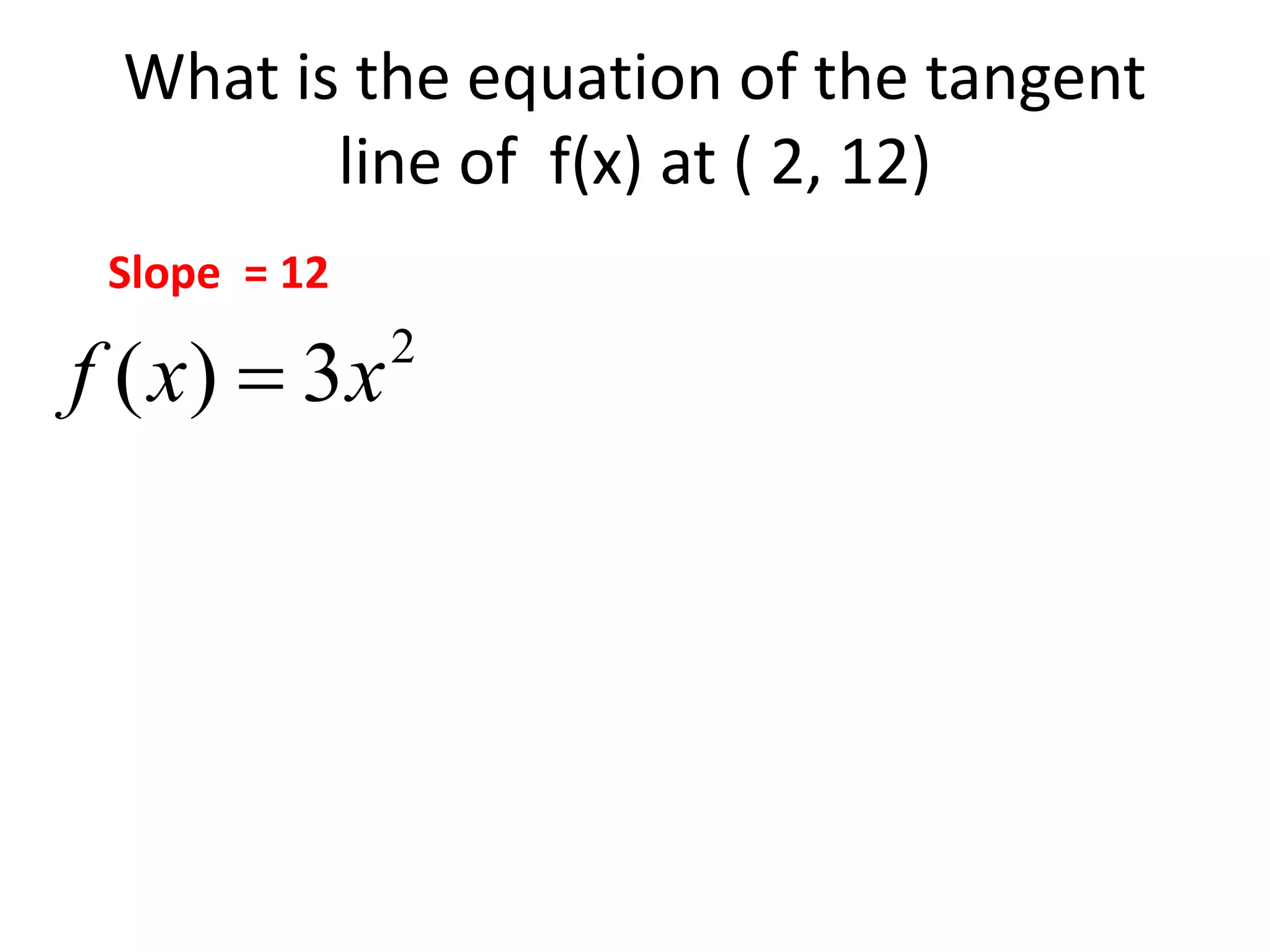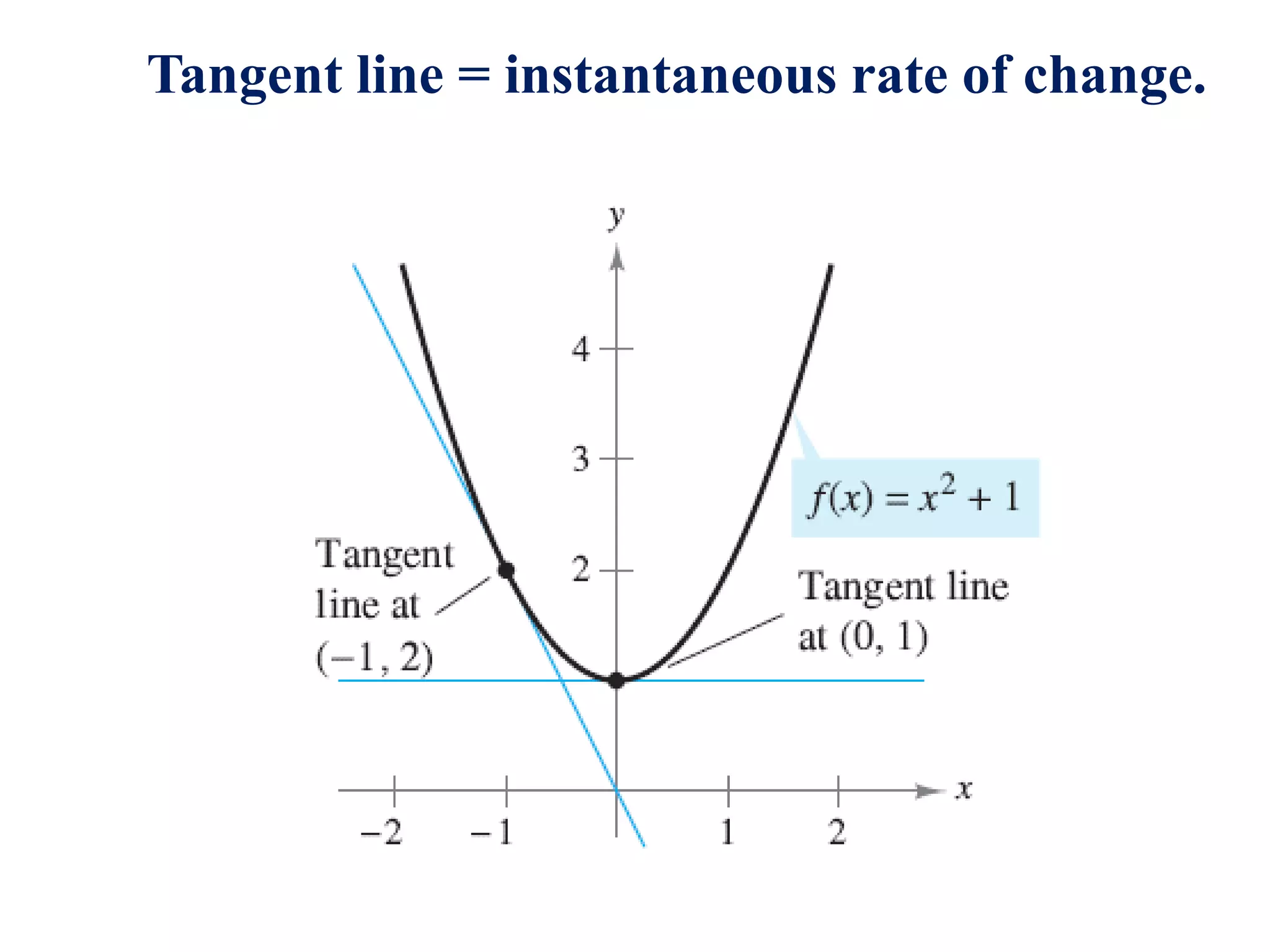
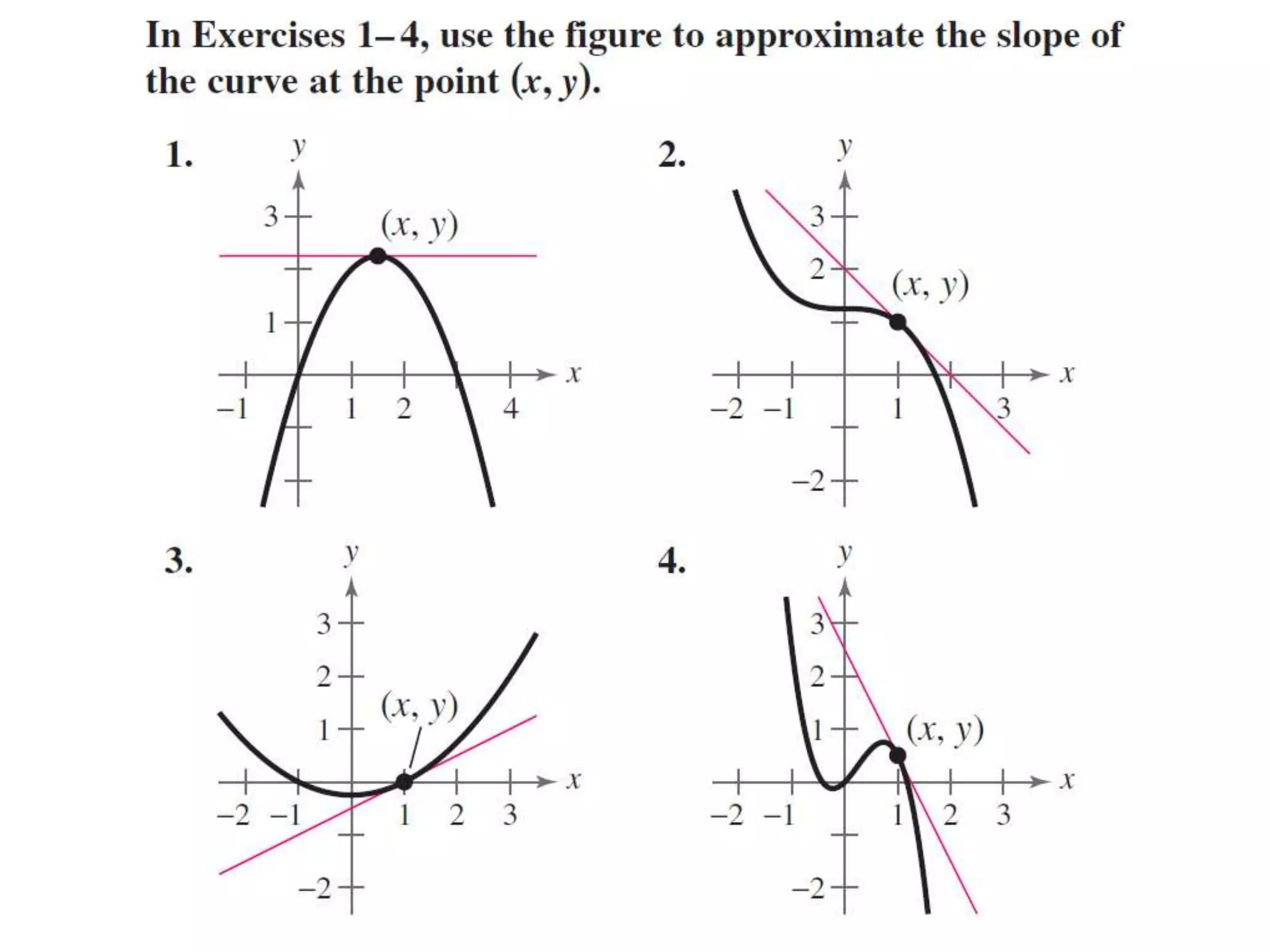
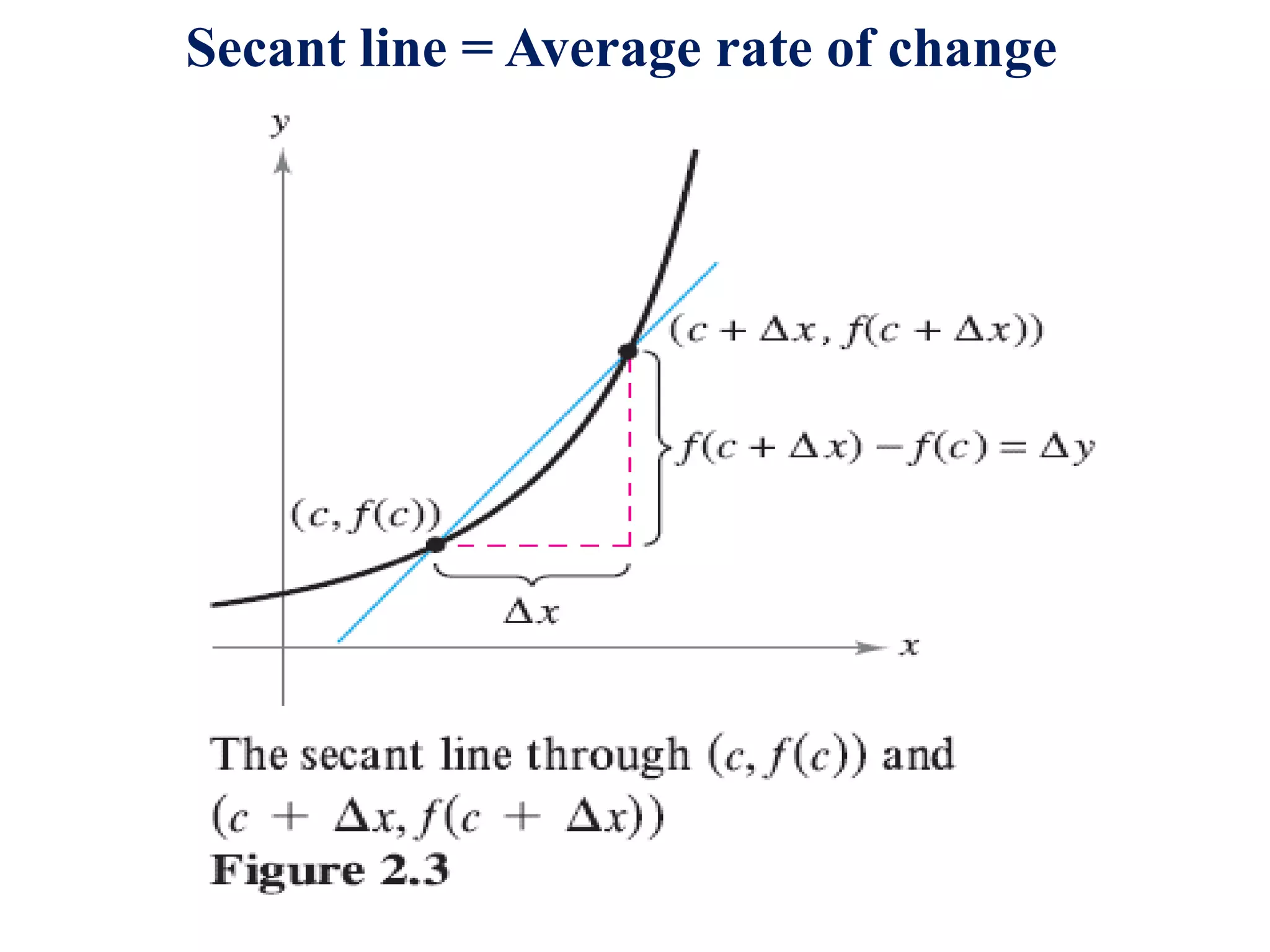
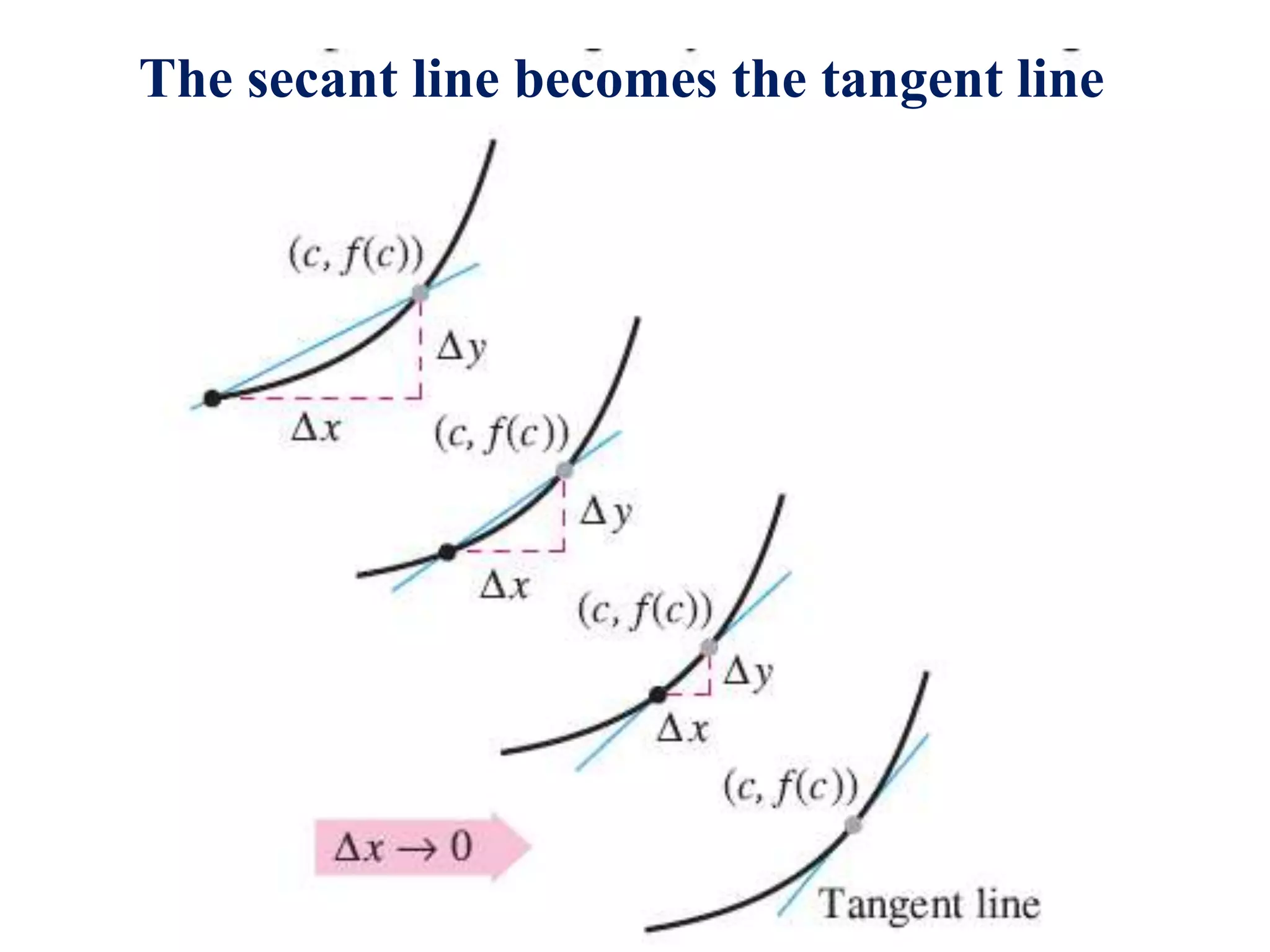
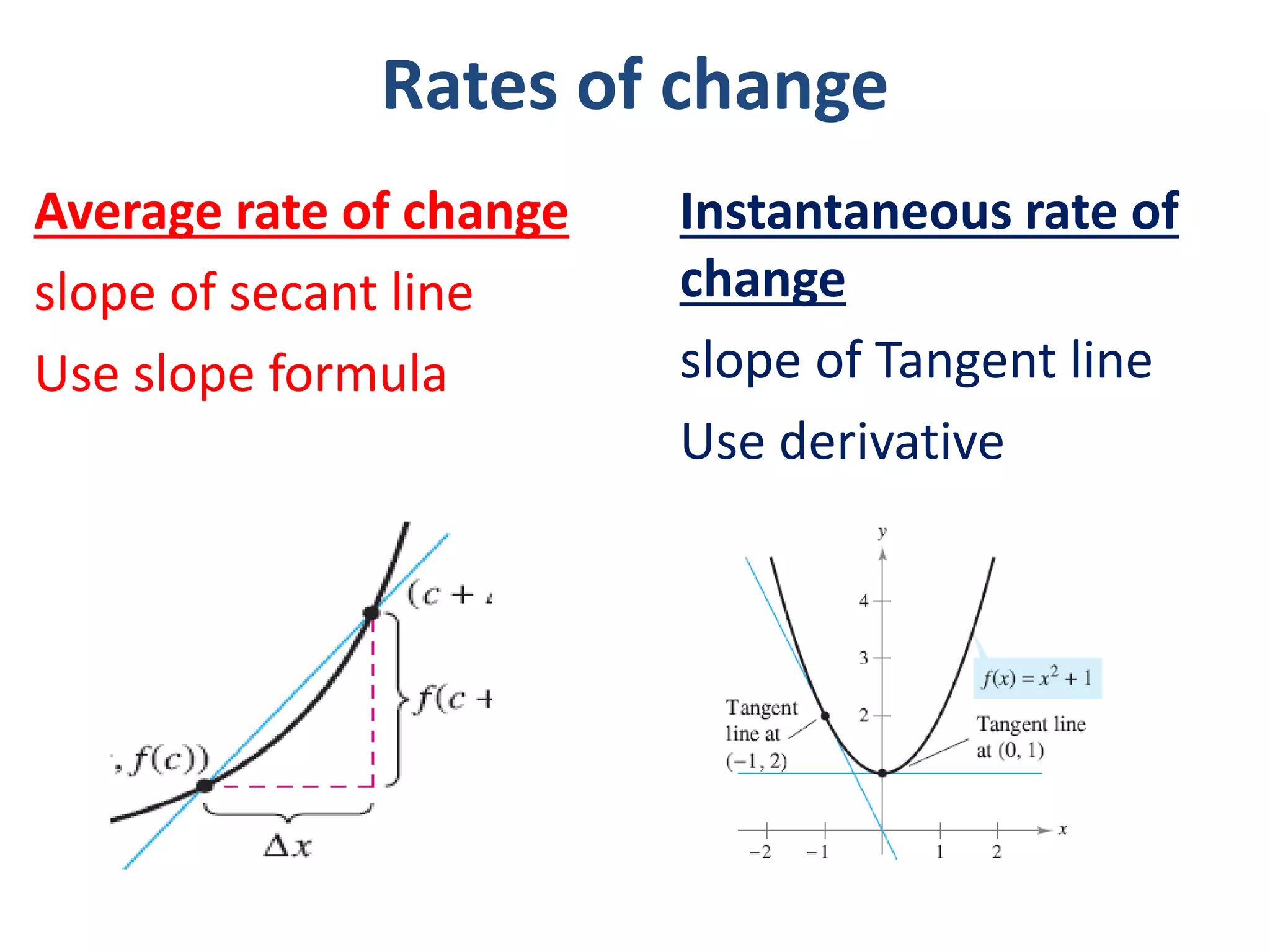
The document discusses key concepts in calculus including: - The derivative of a function gives the instantaneous rate of change or slope of a curve at a given point. - The secant line represents average rate of change, while the tangent line at a point represents instantaneous rate of change. - Differentiation is the process of finding the derivative of a function. A differentiable function has a derivative. 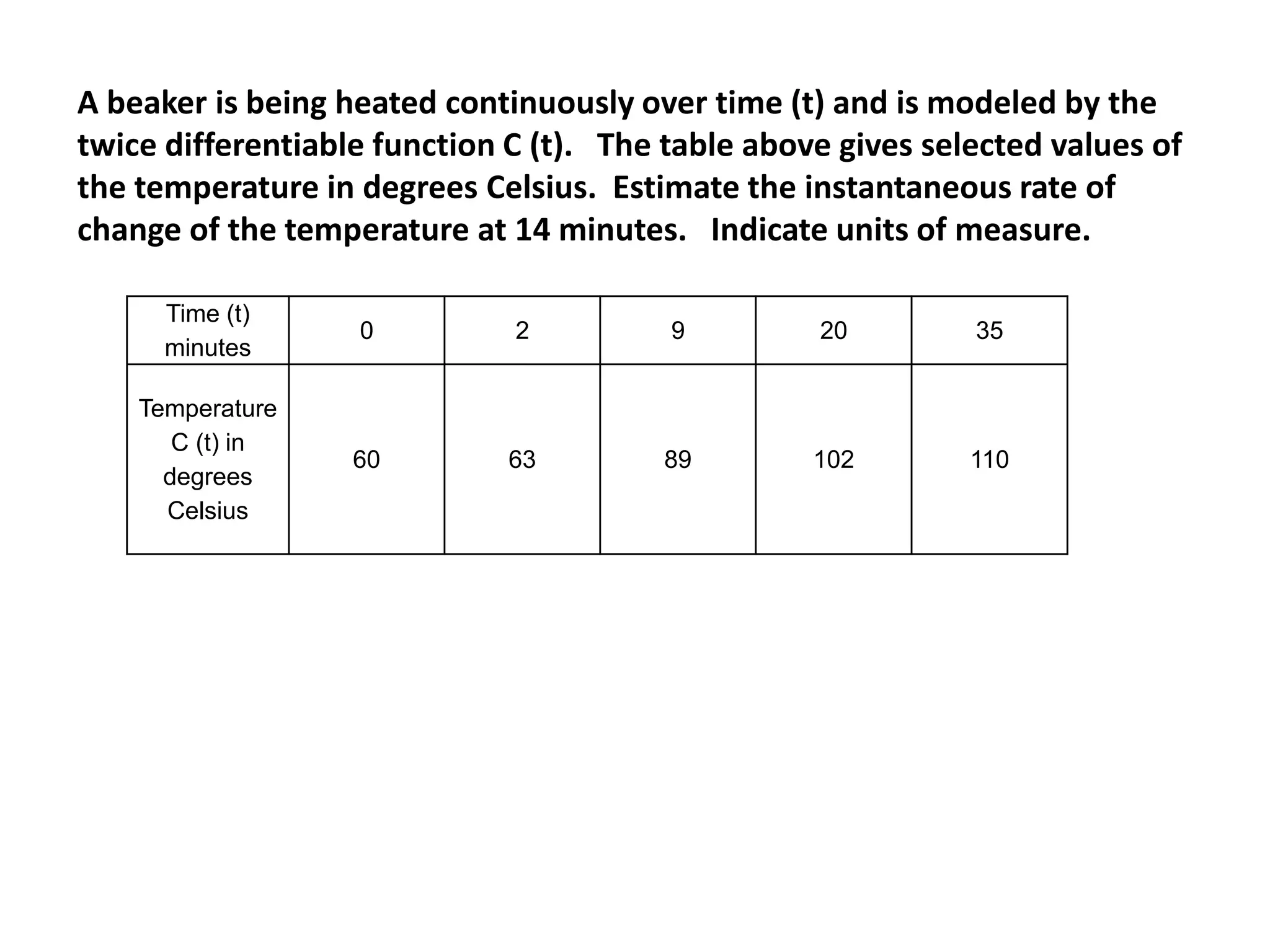- An example problem asks to estimate the instantaneous rate of change of temperature given a temperature function and table of values.

1. AP Calculus Warm up 9.14.18
What is the derivative of a function?
The derivative of a function is also a
function which gives us the instantaneous
rate of change (or slope) of the curve at
any given point.

2. The Lame Joke of the day..
And now it’s time for..
What did one shooting star say to the other?
Pleased to meteor.

3. AP Calculus Warm up 9.14.18
What is the derivative of a function?
The derivative of a function is also a
function which gives us the instantaneous
rate of change (or slope) of the curve at
any given point.

4. Secant line = Average rate of change

5. The secant line becomes the tangent line

7. Tangent line = instantaneous rate of change.

8. Rates of change
Average rate of change
slope of secant line
Use slope formula
Instantaneous rate of
change
slope of Tangent line
Use derivative

10. Differentiation
• The process of finding the derivative of a
function
• If a function has a derivative, it is called
“differentiable”

11. Find the Instantaneous Rate of change
at (2, 12)
2
3)( xxf 

12. What is the equation of the tangent
line of f(x) at ( 2, 12)
2
3)( xxf 
Slope = 12

13. Time (t)
minutes
0 2 9 20 35
Temperature
C (t) in
degrees
Celsius
60 63 89 102 110
A beaker is being heated continuously over time (t) and is modeled by the
twice differentiable function C (t). The table above gives selected values of
the temperature in degrees Celsius. Estimate the instantaneous rate of
change of the temperature at 14 minutes. Indicate units of measure.

14. What makes a function
differentiable?
1. It MUST be continuous.
2. The derivative from the left must equal the
derivative from the right.

15. Most common times when a
derivative does not exist.
1. At a sharp corner 2. At a vertical tangent line
or asymptote

16. KEY POINT
• Differentiability implies continuity,
But continuity DOES NOT imply differentiability.

17. Notation

18. Review
The derivative of a function is also a
function which gives us the instantaneous
rate of change (or slope) of the curve at
any given point.

19. The graph of f is given below.
Sketch out the graph of f ’