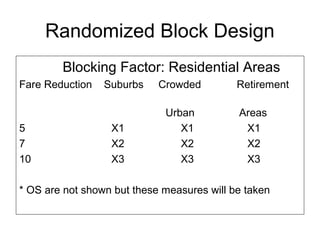
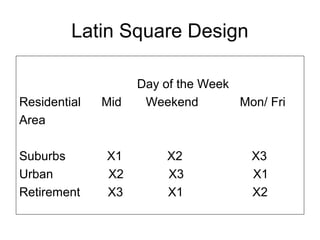
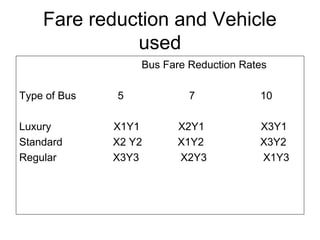
Experimental research designs involve examining potential cause-and-effect relationships between variables through experiments. There are various types of experimental designs including informal designs like quasi-experiments and pre-test/post-test designs, as well as formal designs like completely randomized designs, randomized block designs, Latin square designs, and factorial designs. These designs allow researchers to systematically test and compare the effects of independent variables or treatments on a dependent variable while controlling for other possible influences.

1. Experimental Research
designs

2. Concepts
• Experiment: Lab or Field
• Treatment
• Treatment effects
• Factor-independent variable
• Blocking factor

3. Experimental Design
Examine possible cause and effect
relationship among variables
To establish variable X causes variable Y,
all three conditions should be met:
• Both X and Y should covary
• Time sequence X should precede Y
• No other factor should possibly change
the dependent variable Y

4. Principles of Research Design
• Principle of Replication
• Principle of Randomization
• Principle of Local control

5. Informal Experimental Design
1. Quasi Experimental Design
2. Pretest and posttest Experimental Group
Design ( caution: testing and
instrumentation)
3. Post test only control design
4. Pretest posttest experimental and control
group design

6. Validity
• External – Generalizability to other setting
• Internal- History, maturation effects,
testing, instrumentation, selection bias etc

7. Quasi E.D.
• Experimental group treatment and
measure effects

8. Pre test & Post test ED
Experimental group
Pretest Treatment Post test
O1 X O2
Treatment Effect=(O2-O1)

9. Post test only control design
Group Treatment Outcome
Experimental group X O1
Control group O2
• Treatment Effect=(O1-O2)

10. Pretest posttest experimental and
control group design
Group Pretest Treatment Posttest
Experimental group O1 X O2
Control group O3 O4
Treatment Effect=[(O2-O1)-(O4-O3)]

11. Solomon Four-Group Design
Group Pretest Treatment Posttest
Experimental O1 X O2
Control O3 O4
Experimental X O5
Control O6
Treatment Effect E=O2-O1
=O2-O4
=O5-O6
=O5-O3
=[(O2-O1)-(O4-O3)]
* all Es are similar if cause and effect is highly valid

12. Double blind studies
• Researcher-subjects are unaware
• Drugs

13. Design a study to examine the
following situation.
An organization would like to introduce one
of two types of new manufacturing
processes to increase to the productivity
of the workers, and both involve heavy
investment in expansive technology. The
company wants to test the efficacy of each
process in one of its small plants.

14. Formal E.D.
Completely Randomized
Randomized Block
Latin Square
Factorial
They are required to judge simultaneous
effect of two or more variables on
dependent variable.

15. Concept
• Factor denotes independent variable
• Level denotes various gradations of factor
(high, medium and low price)
• Treatment refers to various levels of
factors
• Blocking factor is a preexisting variable
that has an effect on dependent variable
in addition to the treatment, the impact of
which is important to assess

16. Completely randomized design
A transportation compnay manager wants to
know the effect of fare reduction by 5, 7,
and 10 rupees, on the average increase in
number of passengers using bus as a
means of transportation.
He chooses 27 routes and randomly assign
nine routes to each of treatments for a two
week period.

17. The design would look like
Routes Number of Treatment Number of
passenger before passenger
after
Group 1 O1 X1 O2
Group 2 O3 X2 O4
Group 3 O5 X3 O6
* OS SIGNFY NUMBER OF PASSENGERS

18. Randomized Block Design
Now company manager was interested in targeting
price reduction of right routes or sectors.
Reduction would be more welcomed by the
senior citizens or people living in crowded areas
were driving is a problem than the suburbs.
First the manager would identify the routes fally
into three categories i.e. retirement areas,
crowded areas and suburbs. Thus now 27
routes would get assigned to one or the other of
three blocks and then randomly assigned, within
the blocks to three treatments.

19. Randomized Block Design
Blocking Factor: Residential Areas
Fare Reduction Suburbs Crowded Retirement
Urban Areas
5 X1 X1 X1
7 X2 X2 X2
10 X3 X3 X3
* OS are not shown but these measures will be taken

20. Latin Square Design
Two blocking factor (nuisance) across rows
and columns.
• Day of the week
1. Midweek (Tue to Thrus)
2. Weekend
3. Mon and Friday
• Residential localities

21. Latin Square Design
Day of the Week
Residential Mid Weekend Mon/ Fri
Area
Suburbs X1 X2 X3
Urban X2 X3 X1
Retirement X3 X1 X2

22. Factorial Design
It enables us to check manipulations of two
or more manipulation at the same time on
dependent variable
The manager now is interested in knowing
passenger increases if he used three
different types of buses( Luxury, standard
and regular). Using fare reduction and
type of vehicle simultaneously

23. Fare reduction and Vehicle
used
Bus Fare Reduction Rates
Type of Bus 5 7 10
Luxury X1Y1 X2Y1 X3Y1
Standard X2 Y2 X1Y2 X3Y2
Regular X3Y3 X2Y3 X1Y3

24. Any doubts?
Thank you