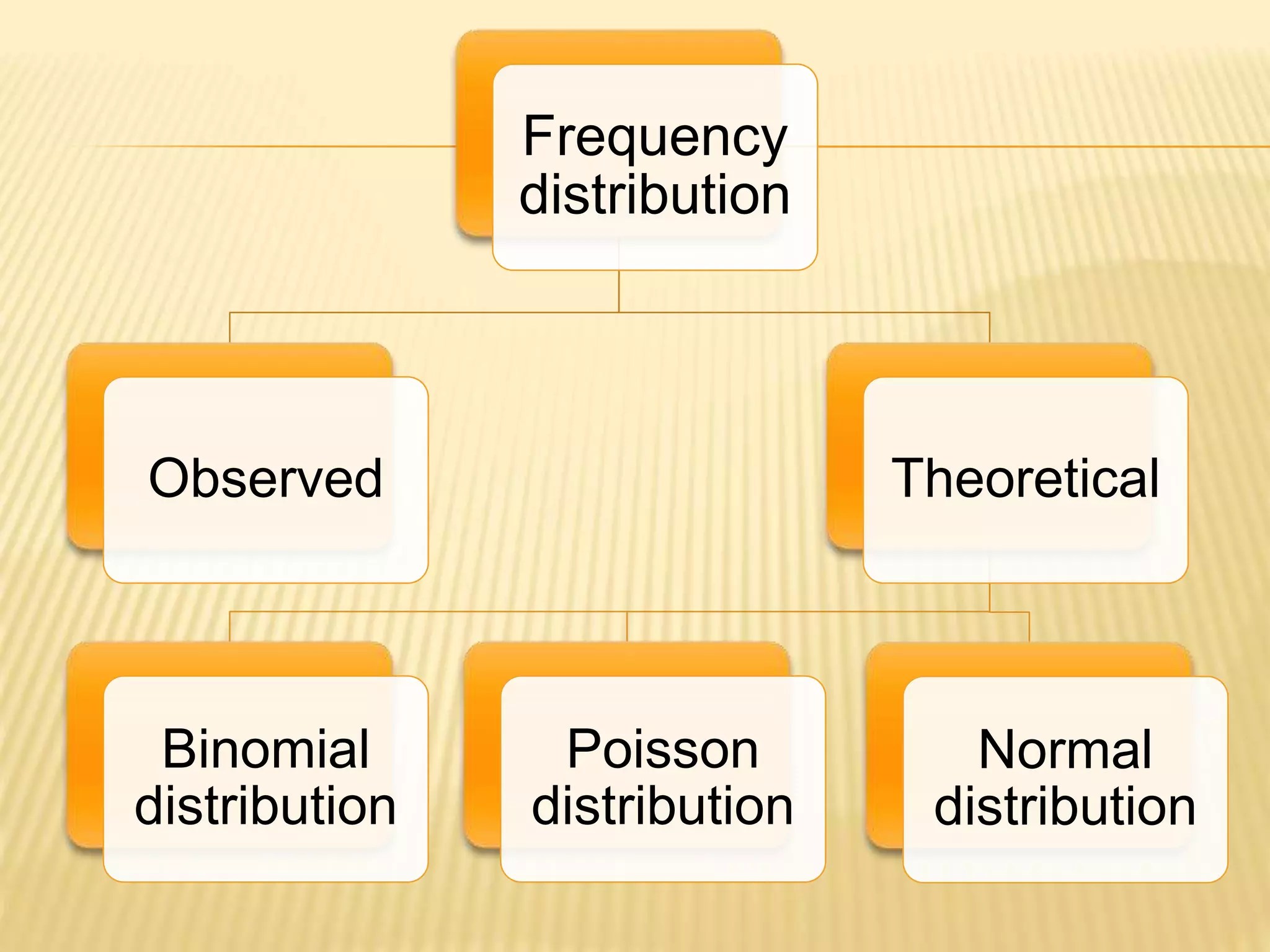
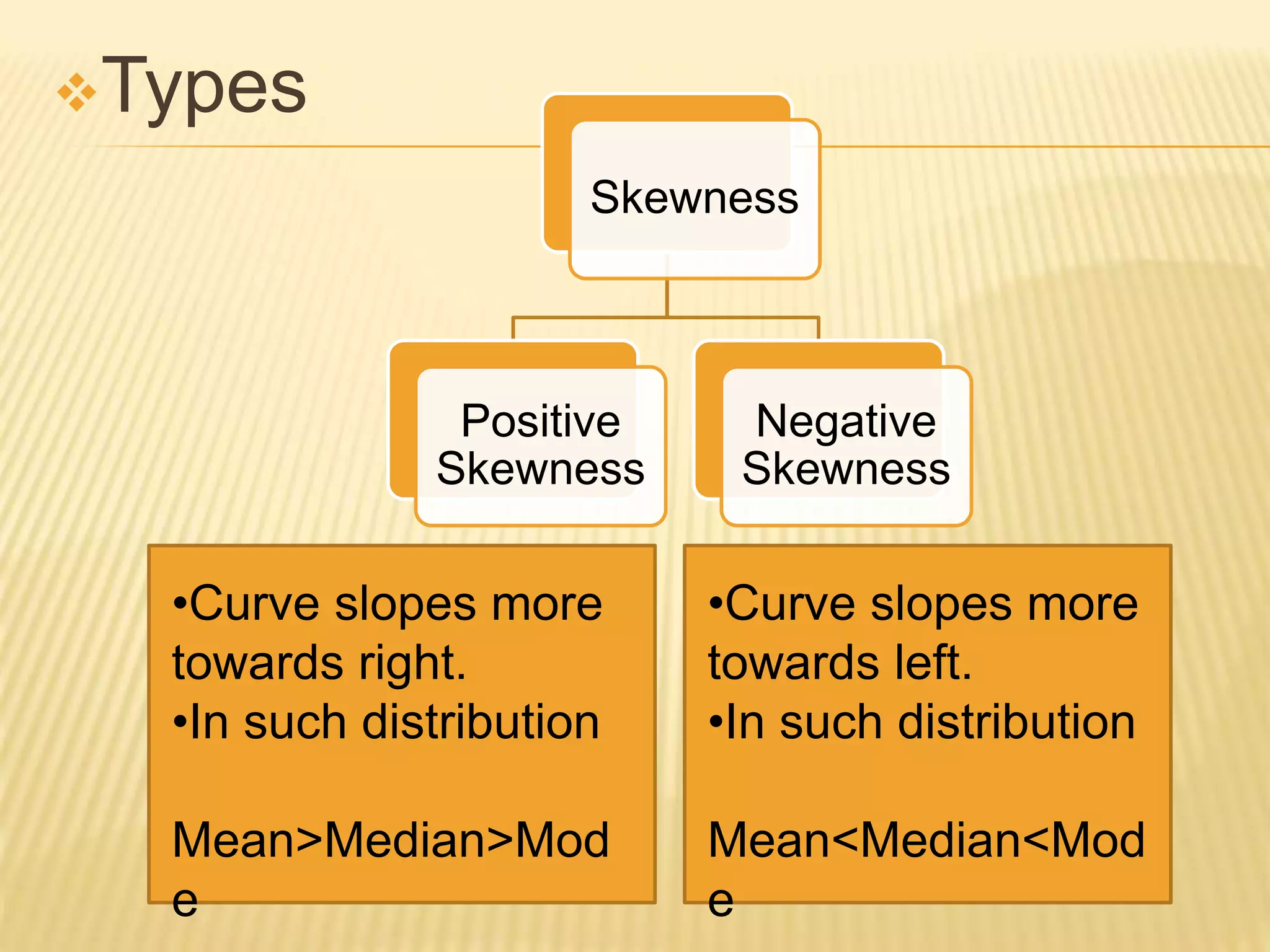
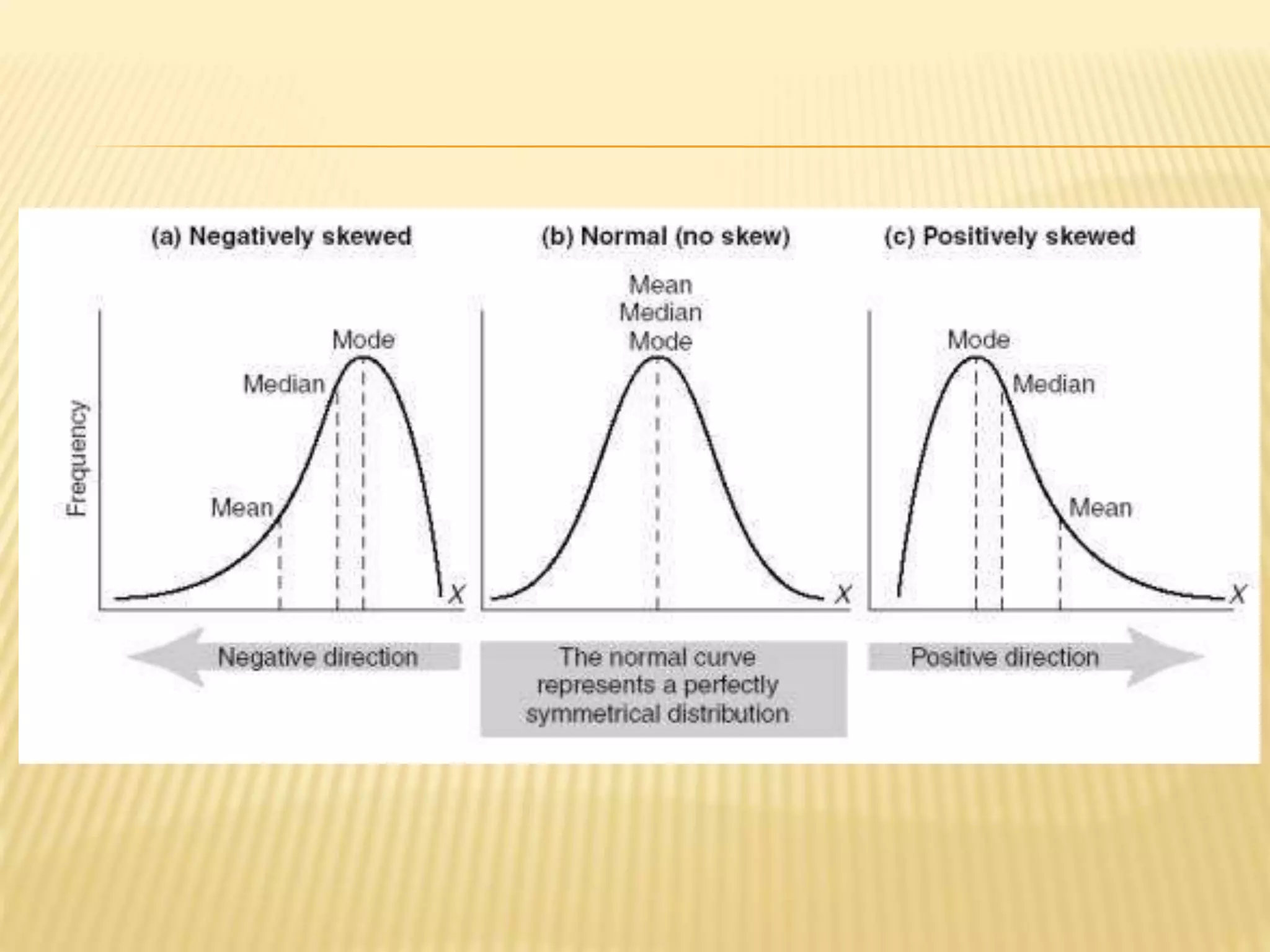
This document explains the concept of skewness in probability and probability distributions, detailing its definition, features, and types, including positive and negative skewness. It discusses the measures of skewness such as absolute skewness, relative skewness, and coefficients like Karl Pearson's and Bowley's. Additionally, it provides examples and mathematical formulas related to calculating skewness in various distributions.

1. SKEWNESS

2. CONTENT
 Introduction - Probability and Probability
distribution
 Skewness
a. Definition
b. Features
c. Types
d. Measures of Skewness
e. Example

3. PROBABILITY
 Def.-It is the chance of occurrence of an
event.
 The value of probability ranges between 0
and 1.
 The probability of the occurrence of the
outcomes deduced mathematically forms a
Probability distribution.
 Probability distribution may be-
1. Discrete probability distribution
2. Continuous probability distribution

4. Frequency
distribution
Observed Theoretical
Binomial
distribution
Poisson
distribution
Normal
distribution

5. NORMAL DISTRIBUTION
 Def.-It represents the
probability
distribution of
frequencies of
continuous variables
, whose frequencies
are concentrated
closely around the
center and gradually
fall towards the two
ends.

6. SKEWNESS
 Def.-Measure of extent of deviation from the
normal distribution.
 The data may be skewed to the left or right.
 Features of skewed distribution
 Curve is not bell shaped.
 Mean , median and mode do not coincide.
 In skewed distribution curve , the first and the
third quartiles of frequency are not equidistant
from median i.e. Q3 – Me ≠ Me –Q1

7. Types
Skewness
Positive
Skewness
Negative
Skewness
•Curve slopes more
towards right.
•In such distribution
Mean>Median>Mod
e
•Curve slopes more
towards left.
•In such distribution
Mean<Median<Mod
e

9. Measure of Skewness
 Skewness can be measured in the terms
of differences between Mean and Mode.
 The various measures of skewness are:-
1. Absolute skewness
2. Relative skewness
3. Standardised skewness
4. Karl Pearson’s coefficient of skewness
5. Bowley’s coefficient of skewness

10. 1. Absolute Skewness
It is the difference between Mean and
Mode.
Skewness=Mean-Mode
2.Relative Skewness
Also called coefficient of skewness.
It is expression of skewness in relative
terms.
Relative skewness= Mean-Mode
Standard

11. 3.Standardised Skewness
•In a distribution , the average of the
powers of deviation from arithmetic mean is
called Moment of distribution(m).
Ex. m1 =Ʃ(X-X)1
N
•These powers determine the sign of
numerator.
Ex.m2 =Ʃ(X-X)2 ; m3 =Ʃ(X-X)3
N N

12. 4.Karl Pearson’s coefficient of
skewness
Skewness(S)=3(Mean-Median)
Standard deviation
5.Bowley’s coefficient of skewness
•Based on Quartiles.
S=Q₃+Q₁-2Median
Q₃-Q₁

13. Ex.
No. Of
eggs
0-2 2-4 4-6 6-8 8-10 10-12 12-14
No. Of
fishes
1 2 4 9 4 3 2
Find Relative skewness.
Ans. S= Mean-Mode
Standard deviation
a.Mean =Ʃfm
Ʃf

14. b.Mode=L₁+ ∆₁ *i
∆₁+∆₂
c. Standard deviation= Ʃfd2
N