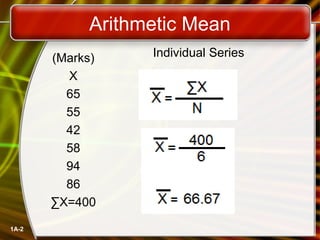
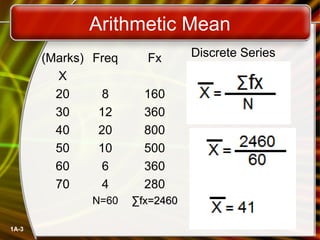
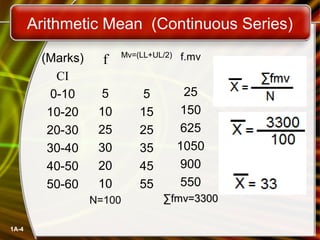
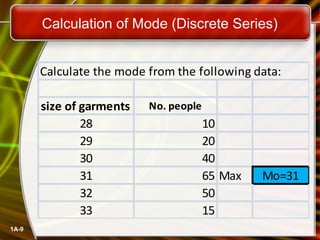
This document discusses calculating measures of central tendency (mean, median, mode) from individual series, discrete series, and continuous series data. It provides examples of calculating the mean, median, and mode from various data sets, including individual data points, frequency distributions, and grouped data. The mean is calculated by summing all values and dividing by the total number of data points. The median is found by ordering the data and taking the middle value. The mode is the value that occurs most frequently for individual data and the class with the highest frequency for continuous data.

1. Problems on Mean, Median and Mode
Presenter: Sherzad

2. 1A-2
Arithmetic Mean
(Marks)
X
65
55
42
58
94
86
ΣX=400
Individual Series

3. 1A-3
Arithmetic Mean
(Marks)
X
20
30
40
50
60
70
Freq Discrete Series
8
12
20
10
6
4
N=60
Fx
160
360
800
500
360
280
ΣΣffxx==22446600

4. 1A-4
Arithmetic Mean (Continuous Series)
(Marks)
CI
0-10
10-20
20-30
30-40
40-50
50-60
Mv=(LL+UL/2)
f
5
10
25
30
20
10
N=100
5
15
25
35
45
55
f.mv
25
150
625
1050
900
550
ΣΣffmmvv==33330000

5. Calculation of Median (Individual Series)
1A-5
From the following data of the wages of 7 workers compute
the median wage
Wages (in ascending order):
108, 110, 112, 115, 116, 120, 140
M = size . of N +
1
th item
= 7 + 1
=
M th item
115
4 ..
2
...
2
=
M

6. Calculation of Median (Discrete Series)
1A-6
From the following data find the value of median:
Income (Rs) No. person (f) Cumulative freq (cf)
80 16 16
100 24 40
150 26 66
180 30 96
200 20 116
250 6 122
N=122
M = size . of N +
1
th item
= 122 + 1
=
150
61.5
2
...
2
=
M
M

7. 1A-7
Calculation of Median (Continuous Series)
100
Calculate the median for the following frequency distribution
200
= =
2
M L L L
= + - -
= + - -
25 30 25
27.74
(100 77)
42
. )
2
1 2 1(
2
=
M
M
N p cf
f
N
Marks No. students (f) Cumulative freq (cf)
5-10 7 7
10-15 15 22
15-20 24 46
20-25 31 77
25-30 42 119
30-35 30 149
35-40 26 175
40-45 15 190
45-50 10 200
N=200

8. 1A-8
Calculation of Mode (Individual Series)
From the following data calculate the value of mode:
3 X No. of times occurred
5 3 2
8 4 2
5 5 3 Max
4 8 1
5 9 1
9
3 Mo=5
4

9. 1A-9
Calculation of Mode (Discrete Series)
Calculate the mode from the following data:
size of garments No. people
28 10
29 20
30 40
31 65 Max Mo=31
32 50
33 15

10. 1A-10
Calculation of Mode (Continuous Series)
Calculate mode from the following data:
Marks No.
0-5 2
5-10 5
10-15 12
15-20 17 class with highest f
20-25 14
25-30 6
30-35 3
35-40 1
Mo L xC
5 18.12
= + D
1 1
D = - =
1 17 12 5
D = - =
2 17 14 3
15 5
5 3
5
1 2
=
+
= +
=
D + D
C
Mo x

11. 1A-11
The End