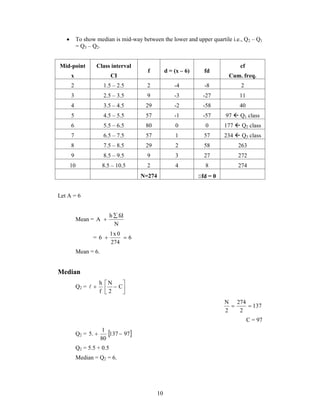
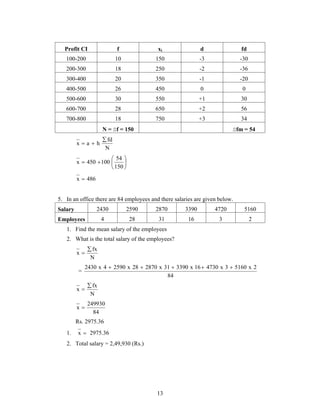
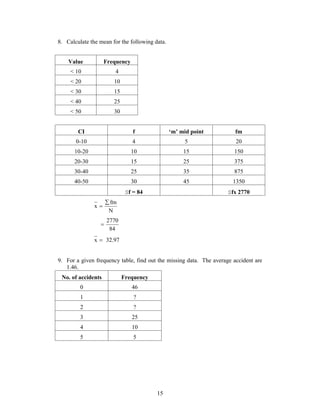
This document discusses measures of central tendency, including the mode, median, quartiles, and percentiles. It provides definitions and formulas for calculating each measure. The mode is defined as the value that occurs most frequently. The median divides the data set into two equal parts. Quartiles divide the data set into four equal parts, with the second quartile being the median. Percentiles divide the data set into 100 equal parts. Several examples are provided to demonstrate calculating the mode, median, quartiles, deciles and percentiles from data sets.

1. Session – 6
Measures of Central Tendency
1
Mode
It is the value which occurs with the maximum frequency. It is the most
typical or common value that receives the height frequency. It represents fashion and
often it is used in business. Thus, it corresponds to the values of variable which occurs
most frequently. The model class of a frequency distribution is the class with highest
frequency. It is denoted by ‘z’.
Mode is the value of variable which is repeated the greatest number of times in
the series. It is the usual, and not casual, size of item in the series. It lies at the
position of greatest density.
Ex: If we say modal marks obtained by students in class test is 42, it means that the
largest number of student have secured 42 marks.
If each observations occurs the same number of times, we can say that there is
‘no mode’. If two observations occur the same number of times, we can say that it is a
‘Bi-modal’. If there are 3 or more observations occurs the same number of times we
say that ‘multi-modal’ case. When there is a single observation occurs mot number of
times, we can say it is ‘uni-modal’ case.
For a grouped data mode can be computed by following equations with usual
notations.
Mode =

h (f f )
m 1
 
2f f f
m 1 2
 
where,
fm = max frequency (modal class frequency)
f1 = frequency preceding to modal class.
f2 = frequency succeeding to modal class
h = class width.
or
Mode =
hf

2
f f
1 2
 

2. 2
Ex:
1. Find the modal for following data.
Marks
(CI)
No. of students
(f)
1 – 10 3
11 – 20 16
21 – 30 26
31 – 40 31  Max. frequency
41 – 50 16
51 – 60 8
f = N = 100
We shall identify the modal class being the class of maximum frequency. i.e.
31-40.
where,
fm = 31
f1 = 26
f2 = 16
h = 10
30  31
2
 
  30.5
Mode (z) =

h (f f )
m 1
 
2f f f
m 1 2
 
Mode =
10 (31 - 26)
2 x 31 26 16
30.5
 

Mode = 33.
Or

3. 10 x 16
3
Mode =
hf

  2
=
f f
1 2
(26 16)
30.5


Mode = 34.30
It can be noted that there exists slightly different mode value in the second
method.
Partition values
Median divides in to two equal parts. There are other values also which
divides the series partitioned value (PV).
Just as one point divides as series in to two equal parts (halves), 3 points
divides in to four points (Quartiles) 9 points divides in to 10 points (deciles) and 99
divide in to 100 parts (percentage). The partitioned values are useful to know the
exact composition of series.
Quartiles
A measure, which divides an array, in to four equal parts is known as quartile.
Each portion contain equal number of items. The first second and third point are
termed as first quartile (Q1). Second quartile (Q2) and third quartile (Qs). The first
quartile is also known as lower quartiles as 25% of observation of distribution below
it, 75% of observations of the distribution below it and 25% of observation above it.
Calculation of quartiles
Q1 = size of
 
item
N 1 th 
4
Q2 = size of
 
item
3 N 1 th 
4
 Q2 = (median) =   
C

N
2
f
 h
Measures of quartiles
The quartile values are located on the principle similar to locating the median
value.

4. Following table shows procedure of locating quartiles.
Individual and Discrete
Measure
senses Continuous series
N 1 th 
2 N 1 th  n item
3 th  n item
4
Q1
 
item
4
item
n th
4
Q2
 
item
4
2 th
4
Q3 N 1 item
4
3 th
4
Ex - 1: From the following marks find Q1, Median and Q3 marks
23, 48, 34, 68, 15, 36, 24, 54, 65, 75, 92, 10, 70, 61, 20, 47, 83, 19, 77
Let us arrange the data in array form.
Sl.
No.
x
1. 10
2. 15
3. 19
4. 20
5. 23 Q1
6. 24
7. 34
8. 36
9. 47
10. 48 Q2
11. 54
12. 61
13. 65
14. 68
15. 70 Q3
16. 75
17. 77
18. 83
19. 92

5. 1  Here, n = 19 items
5
1 th 
a. Q1 = n 1 item
4
Q1 = 19 1
4
1
Q1 = x 20
4
Q1 = 5th item
 Q1 = 23
2 th 
b. Q2 = n 1 item
4
2
Q2 = x 20
4
10th item
 Q2 = 48
3 th 
c. Q3 = n 1 item
4
3
Q3 = x 20
4
= 15th item
 Q3 = 70
Ex - 2: Locate the median and quartile from the following data.
Size of shoes 4 4.5 5 5.5 6 6.5 7 7.5 8
Frequencies 20 36 44 50 80 30 30 16 14
X f cf
4 20 20
4.5 36 56
5 44 100  Q1
5.5 50 150
6 80 230  Q2
6.5 30 260  Q3
7 30 290
7.5 16 306
8 14 320
N = f = 320

6.   N  C
 h
 3
N  C
 and Q3 = 
6
1 th 
Q1 = n 1 item
4
1
Q1 = 321
4
Q1 = 80.25th item
Just above 80.25, the cf is 100. Against 100 cf, value is 5.
 Q1 = 5
1 th 
Q2 = n 1 item
2
1
Q2 = x 321
2
160.5th item
Just above 160.5, the cf is 230. Against 230 cf value is 6.
 Q2 = 6
3 th 
Q3 = n 1 item
4
3
Q3 = x
4
321 = 240.75th item
Just above 240.75, the cf is 260. Against 260 cf value is 6.5.
 Q3 = 6.5
Ex - 3: Compute the quartiles from the following data.
CI 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80
Frequency
5 8 7 12 28 20 10 10
(f)

1
h
First quartile (Q1) = 

4
f


4
f


 h
 N
 
and (Q2) = Median = C and
2
f



7. CI f cf
0-10 5 5
10-20 8 13
20-30 7 20
30-40 12 32  Q1
40-50 28 60  Q2
50-60 20 80  Q3
60-70 10 90
70-80 10 100
N = f = 100
7
a. First locate Q1 for ¼ N
¼ N = 25
 = 30
h = 10
f = 12
c = 20

 h
 1
N  C
(Q1) = 

4
f


30 30 
= 30
2
 
10
Q1 = 30  25 
20
12
Q1 = 34.16
b. Locate Q2 (Median)

40 40 
Q2 corresponds to N/2 = 50, 40
2
 

 h
 N
 C
Q2 = 

2
f

10
Q2 = 40  50 
32
28
Q2 = 46.42

8. 
50 50 
Q3 corresponds to ¾ N = 75, 50
        N  C

D2  & so,on
    P26 = 
 and so, on
8
2
 

 h
 3
N  C
Q3 = 

4
f

10
Q3 = 50 75 
60
20
Q3 = 57.5
Deciles
The deciles divide the arrayed set of variates into ten portions of equal
frequency and they are some times used to characterize the data for some specific
purpose. In this process, we get nine decile values. The fifth decile is nothing but a
median value. We can calculate other deciles by following the procedure which is
used in computing the quartiles.
Formula to compute deciles.
D1 
N C ,
1
10
h
f




2
20
h
f
Percentiles
Percentile value divides the distribution into 100 parts of equal frequency. In
this process, we get ninety-nine percentile values. The 25th, 50th and 75th percentiles
are nothing but quartile first, median and third quartile values respectively.
Formula to compute percentiles is given below:
25
h

P25 = N C ,
100
f



  N  C

26
100
h
f
Ex:
Find the decile 7 and 60th percentile for the given data of patients visited to hospital
on a particular day.
CI f Cf
10-20 1 1
20-30 3 4
30-40 11 15
40-50 21 36
50-60 43 79  P60
60-70 32 111 D70
70-80 9 120
f = N = 120

9. 9

 h
 7
 
a. D7 = N C ,
10
f


60

60 60 
2
 
7 
N 84
10
h = 10, f = 32
c = 79
10
D7 = 60 84 
79
32
7th Decile = D7 = 61.562
b. 60th percentile

 h
 60
N  C
P60 = 

100
f

50

50 50 
2
 
h = 10
f = 43
c = 36
60 
N 72
100
10
P60 = 50 72 
36
43
10
P60 = 50 72 
36
43
P60 = 58.37
SOME NUMERICAL EXAMPLES
1. Show that following distribution is symmetrical about the average. Also shows
that median is the mid-way between lower and upper quartiles.
X 2 3 4 5 6 7 8 9 10
Frequency 2 9 29 57 80 57 29 9 2
 To show the given distribution is symmetrical, Mean, Median and Mode must
be same.

10.  To show median is mid-way between the lower and upper quartile i.e., Q2 – Q1
10
= Q3 – Q2.
Mid-point
x
Class interval
CI
f d = (x – 6) fd
cf
Cum. freq.
2 1.5 – 2.5 2 -4 -8 2
3 2.5 – 3.5 9 -3 -27 11
4 3.5 – 4.5 29 -2 -58 40
5 4.5 – 5.5 57 -1 -57 97  Q1 class
6 5.5 – 6.5 80 0 0 177  Q2 class
7 6.5 – 7.5 57 1 57 234  Q3 class
8 7.5 – 8.5 29 2 58 263
9 8.5 – 9.5 9 3 27 272
10 8.5 – 10.5 2 4 8 274
N=274 fd = 0
Let A = 6
Mean =
h fd
N
A


1x 0
6  
= 6
274
Mean = 6.
Median

 h
 N
 C
Q2 = 

2
f

137
N  274

2
2
C = 97
1
Q2 = 5.  137 
97
80
Q2 = 5.5 + 0.5
Median = Q2 = 6.

11.   Modal class 5.5 – 6.5
11
Mode
Mode =
 

h f f
 
m 1
2f f f
m 1 2
Mode =
 

1 80 57
2 x 80 57 57
5.5
 

Mode = 6.
Since, Mean = Mode = Median. The given distribution is symmetrical.
Q1 calculation

 h
 4
N  C
Q1 = 

2
f

1
Q1 = 6.5  68.5 
40
57
 Q1 = 7.
Now, Q2 – Q1 = Q3 – Q2
i.e. 6 – 5 = 7 – 5
2 = 2
2. Find the mean for the set of observations given below.
6, 7, 5, 4
6 8 7 8 4
5

N
xi
x i 1
n
   
 
30 
= 6
5
3. Find the mean for the following data.
CI f xi fx
0-10 3 5.5 16.5
11-20 16 15.5 248
21-30 26 23.5 683
31-40 31 35.5 1180.5
41-50 16 45.5 728
51-60 8 55.5 444
N = f = 100 3300

12. 12
3200
100
fx


x 
N
x  32
4. Find the mean profit of the organisation for the given data below:
Profit CI f xi fx
100-200 10 150 1500
200-300 18 250 4500
300-400 20 350 7000
400-500 26 450 11700
500-600 30 550 16500
600-700 28 650 18200
700-800 18 750 13500
N = f = 150 72900
x1 =
100  200
2
x1 =
300
2
x1 = 150
fx
N
x


=
72900
150
x  486
Step Deviation Method
x = a + hd  d =
x  a
h
fd
N
x a h

 
a = Arbitrary constant
h = class width

13. Profit CI f xi d fd
100-200 10 150 -3 -30
200-300 18 250 -2 -36
300-400 20 350 -1 -20
400-500 26 450 0 0
500-600 30 550 +1 30
600-700 28 650 +2 56
700-800 18 750 +3 34
N = f = 150 fm = 54
2430 x 4  2590 x 28  2870 x 31  3390 x 16 4730 x 3  5160 x 2
13
fd
N
x a h

 


  

54
150
x 450 100
x  486
5. In an office there are 84 employees and there salaries are given below.
Salary 2430 2590 2870 3390 4720 5160
Employees 4 28 31 16 3 2
1. Find the mean salary of the employees
2. What is the total salary of the employees?
fx
N
x


=
84
fx
N
x


249930
84
x 
Rs. 2975.36
1. x  2975.36
2. Total salary = 2,49,930 (Rs.)

14. 6. The average marks secured by 36 students was 52 but it was discovered that on
item 64 was misread as 46. Find the correct me of the marks.
14
fx
N
x


fx
56
52


fx = 52 x 36 = 1872
fx = fx - incorrect + correct
correct = 1872 – 46 64 = 1890
x 
fx correct
N
x 
1890
36
x  52.5
7. The mean of 100 items is 46, later it was discovered that an item 16 was misread
as 61 and another item 43 was misread as 34 and also found that the total number
of items are 90 not 100 find the correct mean value.
fx
N
x


fx
100
46


fx = 4600
fx = fx - incorrect + correct
= 4600– 61 - 34 + 16 + 43
= 4564
x 
fx correct
N
x 
4564
90
= 50.71

15. 8. Calculate the mean for the following data.
15
Value Frequency
< 10 4
< 20 10
< 30 15
< 40 25
< 50 30
CI f ‘m’ mid point fm
0-10 4 5 20
10-20 10 15 150
20-30 15 25 375
30-40 25 35 875
40-50 30 45 1350
f = 84 fx 2770
fm
N
x


2770 
84
x  32.97
9. For a given frequency table, find out the missing data. The average accident are
1.46.
No. of accidents Frequency
0 46
1 ?
2 ?
3 25
4 10
5 5

16. 16
No. of accidents
(x)
Frequency
(f)
fx
0 46 0
1 ? f1
2 ? 2f1
3 25 75
4 10 40
5 5 25
N = 200 fx = 140 + f1 + 2f2
1.46 =
140 f 2f 1 2  
200
292 = 140 + f1 + 2f2
 f1 + 2f2 = 152 ----(1)
w.k.t. N = f
200 = 86 + f1 + f2
f1 + f2 = 114 ----(2)
f1 + 2f2 = 152 ----(1)
f1 + f2 = 114 ----(2) (1) – (2)
---------------------------------
f2 = 38
---------------------------------
 f2 = 38
f1 + f2 = 114
f1 + 114 – 38
f1 = 76

17. 10. Find out the missing values of the variate for the following data with mean is
17
31.87.
xi F
12 8
20 16
27 48
33 90
? 30
54 8
N = 200
xi f fx
12 8 96
20 16 320
27 48 1296
33 90 2970
x 30 30x
54 8 432
N = 200 fx = 5114 + 30x
x  31.87
fx
N
x


fx
200
31.87


fx = 6374 ----(1)
fx = 5114 + 30x ----(2)
(1) = (2)
6374 = 5114 + 30x
6374 - 5114 = 30x
30x = 1260
x = 42.

18. 11. The average rainfall of a city from Monday to Saturday is 0.3 inches. Due to
heavy rainfall Sunday the average rainfall for the week increased to 0.5 inches.
What is the rainfall on Sunday?
Given: Mon – Sat = 0.3”
Sun = 0.5”
 fx1 = 1.8
 fx2 = 3.5
18


fx
x 1 N

fx
0.3 1 6


fx
x 2 N

fx
0.5 2 7
Rainfall on Sunday = fx2 – fx1
= 3.5 – 1.8
= 1.7”
12. The average salary of male employees in a firm was Rs. 520 and that of females
Rs. 420 the mean of salary of all the employees as a whole is Rs. 500. Find the
percentage of male and female employees.
Given: x 520 1  x 420 2  x 500
n1 = Male persons. n2 = Female persons.

n x n x
1 1 2 2
n n
1 2
x



n x 520 n x 420
1 2
n n
1 2
500



520n 420n
1 2
n n
1 2
500


500n1 + 500n2 = 520n1 – 420n2
80n2 = 20n1
n1 = 4n2
Let n1 + n2 = 100
4n2 + n2 = 100
5n2 = 100
n2 = 20%  Female
n1 = 80%  Male
20% and 80%  are male and females in the firm.

19. 13. The A-M of two observations is 25 and there GM is 15. Find the HM.
19
Given:
AM = 25
a b
2
x


a b
2
x


a b
2
25


a + b = 50
GM = 15
GM = 2 ab
GM = ab
15 = ab
(15)2 = ( ab )2
ab = 225
HM = ?
HM =
1
b
1
a
2

HM =
2ab

a b
HM =
2 x 225
50
HM = 9
a + b = 50
ab = 225
a =
225
b
HM = 9
14. The GM is 60 an HM is 28.24. Find AM for two observations.
AM GM HM
a b
2
x


254 95b
2
x


= 127.475
60 = ab
602 = ab
ab = 3600
28.24 =
2ab

a b
a + b =
2ab
28.4
=
2 x 3600
28.4
a + b = 254.95

20. 15. Calculate the missing frequency from the data if the median is 50.
CI f cf
10-20 2 2
20-30 8 10
30-40 6 16
40-50 ? f1 16+f1
50-60 15 31+f1  median class
60-70 10 41+f1
20
f = 41 + f1

 h
 N
 C
Q = 

2
f


  (16  f )
2
10
50 = 50 + 

N
15

  (16  f )
2
10
1 50 – 50 = 

N
15
1

  (16  f )
2
10
0 = 

N
15

  (16  f )
2
1 0 = 

N
10 1

  (16  f )
2
0 = 

N
1
N
(16  f ) 
1 2
16 + f1 = ½ (41 + f1)
2 (16 + f1) = 41 + f1
32 + 2f1 = 41 + f1
f1 = 9

21. SOURCES AND REFERENCES
1. Statistics for Management, Richard I Levin, PHI / 2000.
2. Statistics, RSN Pillai and Bagavathi, S. Chands, Delhi.
3. An Introduction to Statistical Method, C.B. Gupta, & Vijaya Gupta, Vikasa
21
Publications, 23e/2006.
4. Business Statistics, C.M. Chikkodi and Salya Prasad, Himalaya Publications,
2000.
5. Statistics, D.C. Sancheti and Kappor, Sultan Chand and Sons, New Delhi, 2004.
6. Fundamentals of Statistics, D.N. Elhance and Veena and Aggarwal, KITAB
Publications, Kolkata, 2003.
7. Business Statistics, Dr. J.S. Chandan, Prof. Jagit Singh and Kanna, Vikas
Publications, 2006.