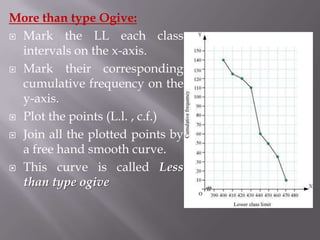
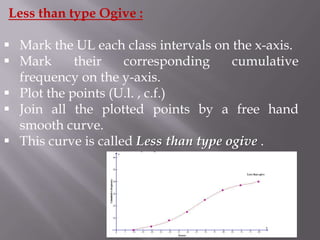
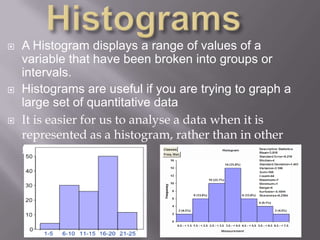
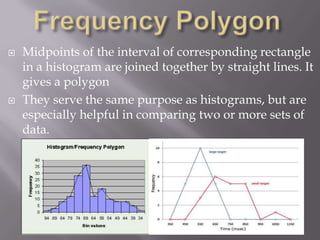
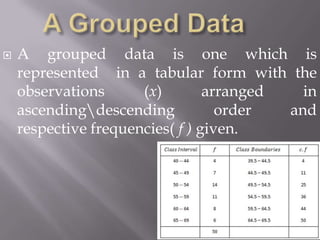
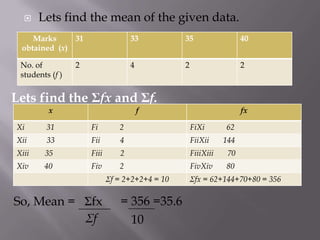
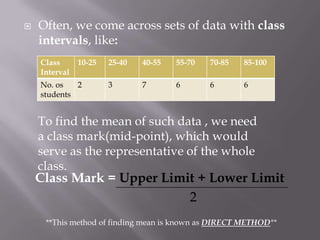
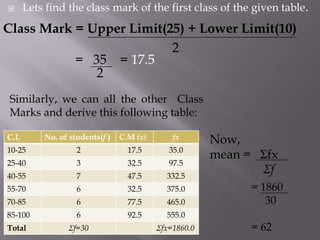
This document discusses various statistical concepts taught in 9th grade including histograms, frequency polygons, and numerical representatives of ungrouped data. It then introduces concepts related to grouped data such as calculating the mean, median, and mode of grouped data using different methods like the direct method, assumed mean method, and step deviation method. It also discusses the concepts of cumulative frequency, ogives (cumulative frequency curves), and how to find the median from an ogive.

1. -- B. Kedhar Guhan --
-- X D --
-- 34 --

2. In this PPT, we would first recap what we had learnt
in 9th.-
• Histograms : SLIDE 3
• Frequency polygons: SLIDE 4
• Numerical representatives of ungrouped data:
SLIDE 5

3. Then we sneak-a-peek on-
 Central Tendencies of a Grouped Data: SLIDE 7
 Grouped Data : SLIDE 8
 Mean of a grouped data: SLIDE 9
 Direct Method: SLIDE 11
 Assumed mean method: SLIDE 13
 Step deviation Method: SLIDE 15
 Mode: SLIDE 16
 Concept of Cumulative Frequency: SLIDE 17
• Median: SLIDE 18
• Ogives : SLIDE 20

4.  A Histogram displays a range of values of a
variable that have been broken into groups or
intervals.
 Histograms are useful if you are trying to graph a
large set of quantitative data
 It is easier for us to analyse a data when it is
represented as a histogram, rather than in other
forms.

5.  Midpoints of the interval of corresponding rectangle
in a histogram are joined together by straight lines. It
gives a polygon
 They serve the same purpose as histograms, but are
especially helpful in comparing two or more sets of
data.

6. 1. Arithmetic Mean: (or Average)
• Sum of all observation divided by
the Number of observation.
• Let x1,x2,x3,x4 ….xn be obs.( thus
there are „n‟ number of scores)
Then Average =
(x1+x2+x3+x4 ….+xn)/n

7. 2 Median: When the data is arranged
in ascending or descending order,
the middle observation is the
MEDIAN of the data. If n is even,
the median is the average of the
n/2nd and (n/2+1/2 )nd observation.
3 Mode: It is the observation that has
the highest frequency.

8.  A grouped data is one which is
represented in a tabular form with the
observations (x) arranged in
ascendingdescending order and
respective frequencies( f ) given.

9.  To obtain the mean,
1. First, multiply value of each observation(x) to
its respective frequency( f ).
2. Add up all the obtained values(fx).
3. Divide the obtained sum by the total no. of
observations.
MEAN =

10.  Lets find the mean of the given data.
Marks 31 33 35 40
obtained (x)
No. of 2 4 2 2
students (f )
Lets find the Σfx and Σf.
x f fx
Xi 31 Fi 2 FiXi 62
Xii 33 Fii 4 FiiXii 144
Xiii 35 Fiii 2 FiiiXiii 70
Xiv 40 Fiv 2 FivXiv 80
Σf = 2+2+2+4 = 10 Σfx = 62+144+70+80 = 356
So, Mean = Σfx = 356 =35.6
Σf 10

11.  Often, we come across sets of data with class
intervals, like:
Class 10-25 25-40 40-55 55-70 70-85 85-100
Interval
No. os 2 3 7 6 6 6
students
To find the mean of such data , we need
a class mark(mid-point), which would
serve as the representative of the whole
class.
Class Mark = Upper Limit + Lower Limit
2
**This method of finding mean is known as DIRECT METHOD**

12.  Lets find the class mark of the first class of the given table.
Class Mark = Upper Limit(25) + Lower Limit(10)
2
= 35 = 17.5
2
Similarly, we can all the other Class
Marks and derive this following table:
C.I. No. of students(f ) C.M (x) fx Now,
10-25 2 17.5 35.0
mean = Σfx
25-40 3 32.5 97.5
40-55 7 47.5 332.5
Σf
55-70 6 32.5 375.0 = 1860
70-85 6 77.5 465.0 30
85-100 6 92.5 555.0
Total Σf=30 Σfx=1860.0 = 62

13.  Another method of finding MEAN:
1. Choose one of the observation as the “Assumed
Mean”. [select that xi which is at the centre of
x1, x2,…, xn.
2. Then subtract a from each class mark x to
obtain the respective d value (x-a).
3. Find the value of FnDn, where n is a particular
class; F is the frequency; and D is the obtained
value.

14. Mean of the data= mean of
the deviations =

15. 1. Follow the first two steps as in Assumed Mean
method.
2. Calculate u = xi-a
h
3. Now, mean = x = a+h { },
Σ fu
Σf
Where
h=size of the CI
f=frequency of the modal class
a= assumed mean

16. The class with the highest frequency is
called the MODAL CLASS
C.I. No. of C.M fx
students(f ) (x) In this set of
10-25 2 17.5 35.0 data, the class
25-40 3 32.5 97.5
“40-55” is the
40-55 7 47.5 332.5
55-70 6 32.5 375.0
modal class as
70-85 6 77.5 465.0 it has the
85-100 6 92.5 555.0 highest
Total Σf=30 Σfx=1860
frequency

17.  It‟s the „running total‟ of frequencies.
 It‟s the frequency obtained by adding the of all
the preceding classes.
 When the class is taken as less than [the Upper
limit of the CI], the cumulative frequencies is
said to be the less than type.
 When the class is taken as more than [the lower
limit of the CI], the cumulative frequencies is
said to be the more than type.

18.  If n ( no. of classes) is odd, the median is
{(n+1)/2}nd class.
 If n is even, then the median is the average of
n/2nd and (n/2 + 1)th class.
 Median for a grouped data is given by
Median = l{ n/2f- cf }h
Where
l= Lower Limit of the class
n= no. of observations
cf= cumulative frequency of the preceding class
f= frequency
h= class size

19. 3 Median = Mode + 2 Mean

20.  Cumulative frequency distribution can be
graphically represented as a cumulative
frequency curve( Ogive )

21. More than type Ogive:
 Mark the LL each class
intervals on the x-axis.
 Mark their corresponding
cumulative frequency on the
y-axis.
 Plot the points (L.l. , c.f.)
 Join all the plotted points by
a free hand smooth curve.
 This curve is called Less
than type ogive

22. Less than type Ogive :
 Mark the UL each class intervals on the x-axis.
 Mark their corresponding cumulative
frequency on the y-axis.
 Plot the points (U.l. , c.f.)
 Join all the plotted points by a free hand
smooth curve.
 This curve is called Less than type ogive .

23. METHOD 1
 Locate n/2 on the y-axis.
 From here, draw a line parallel to x-axis, cutting
an ogive ( less/more than type) at a point.
 From this point, drop a perpendicular to x-axis.
 The point of intersection of this perpendicular
and the x-axis determines the median of the
data.

24. METHOD 2:
 Draw Both the Ogives of the data.
 From the point of intersection of these
Ogives, draw a perpendicular on the x-axis.
 The point of intersection of the
perpendicular and the x-axis determines.

25. -- B. Kedhar Guhan --
-- X D --
-- 34 --