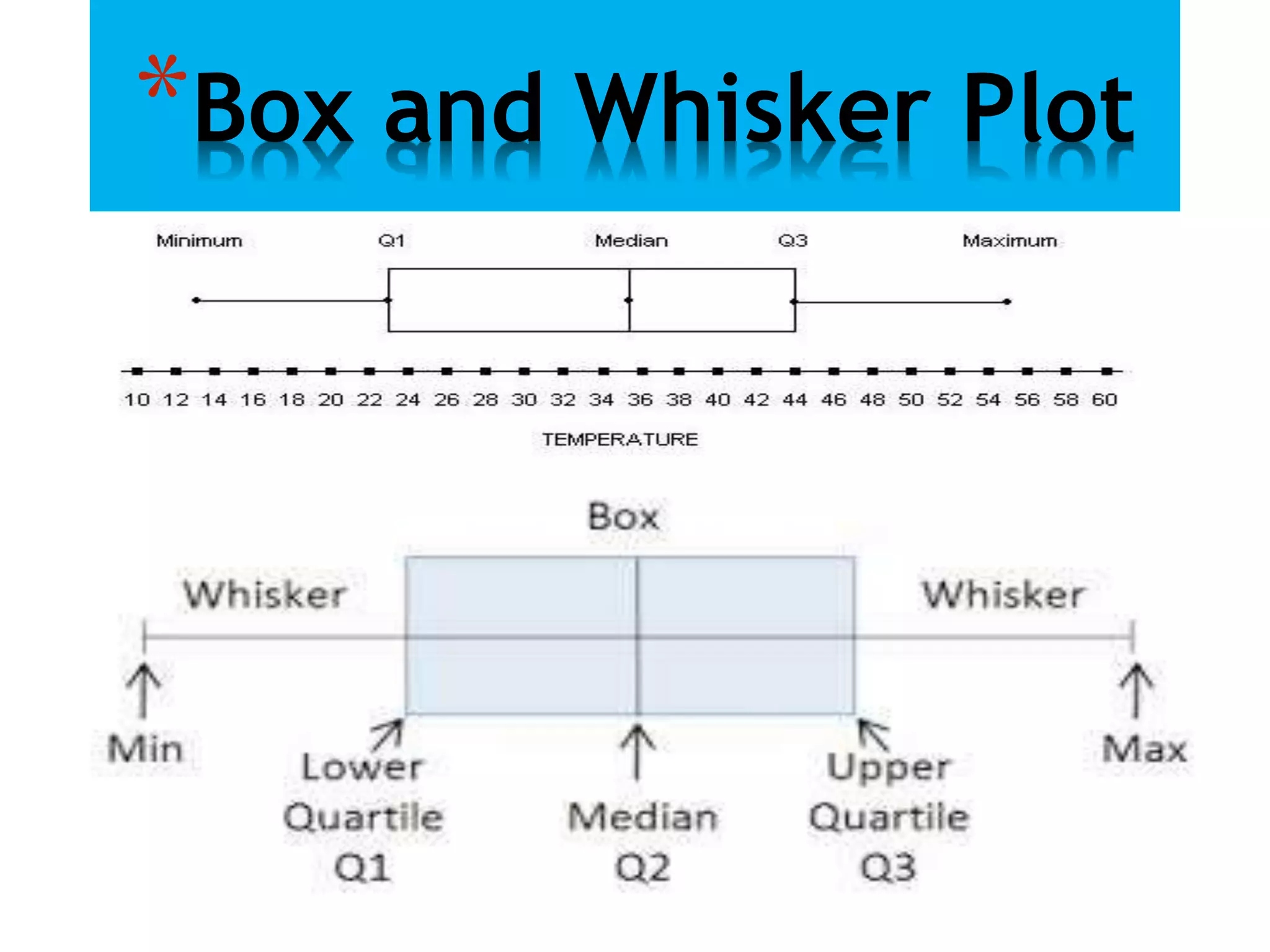
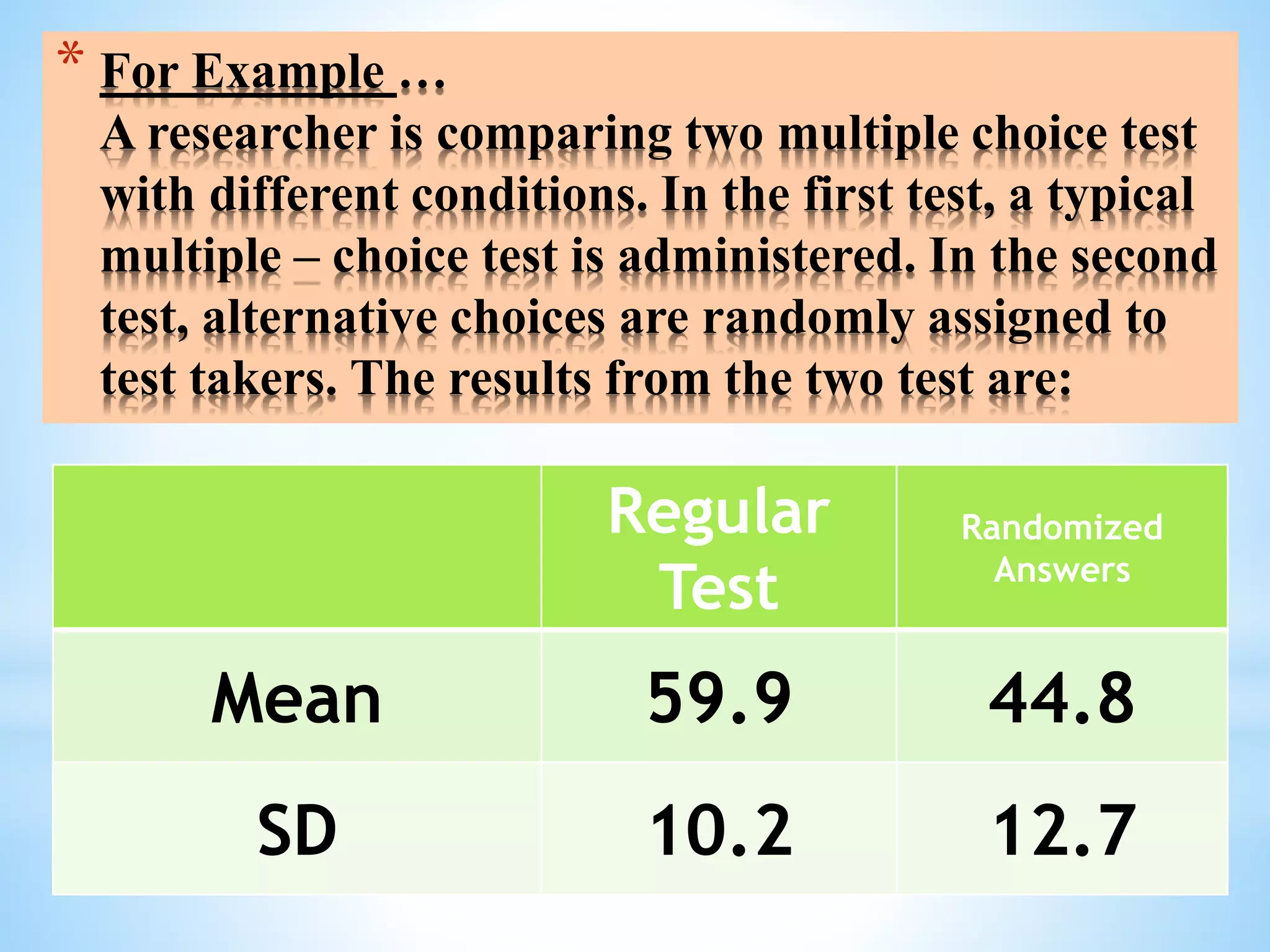
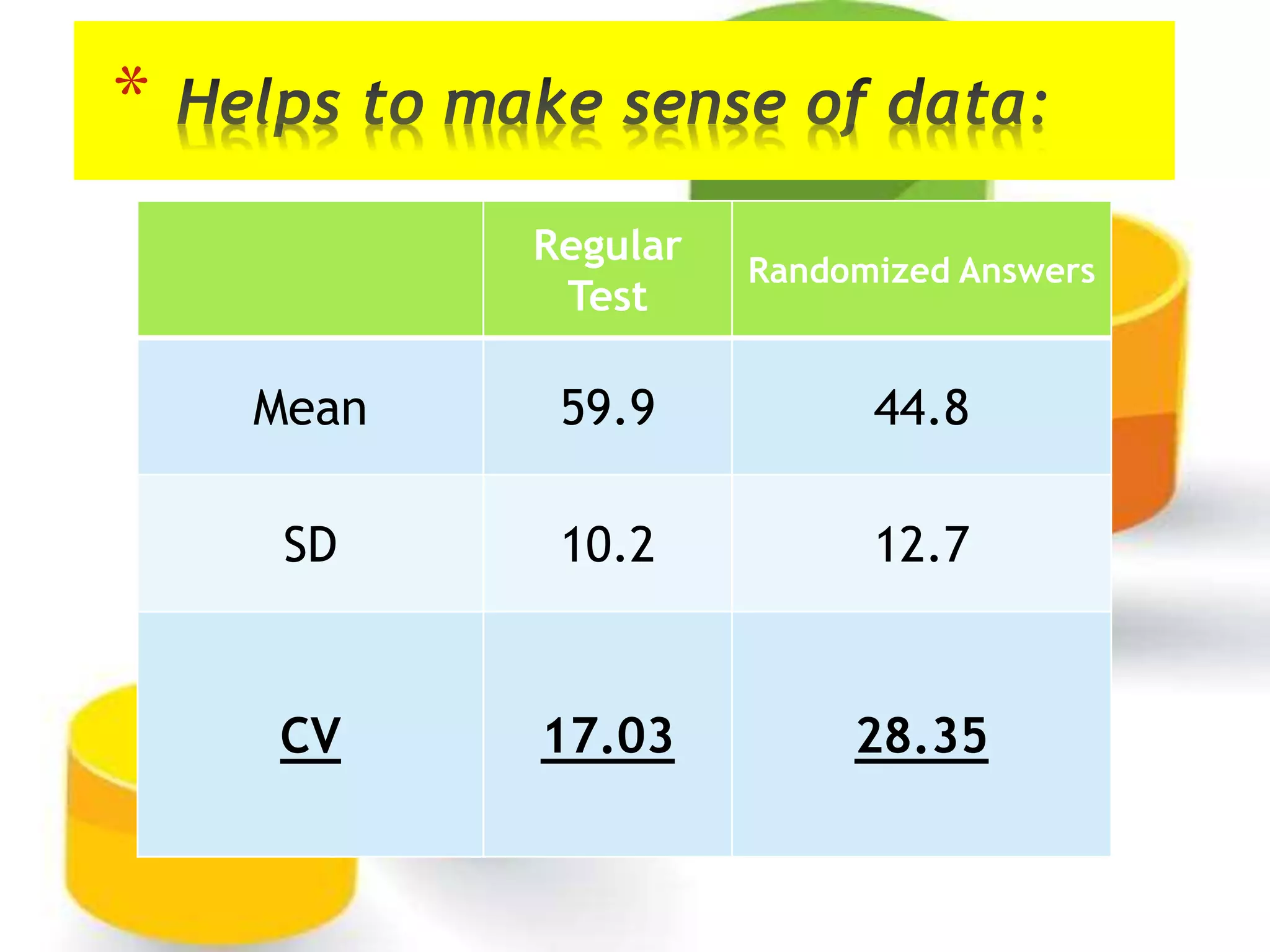
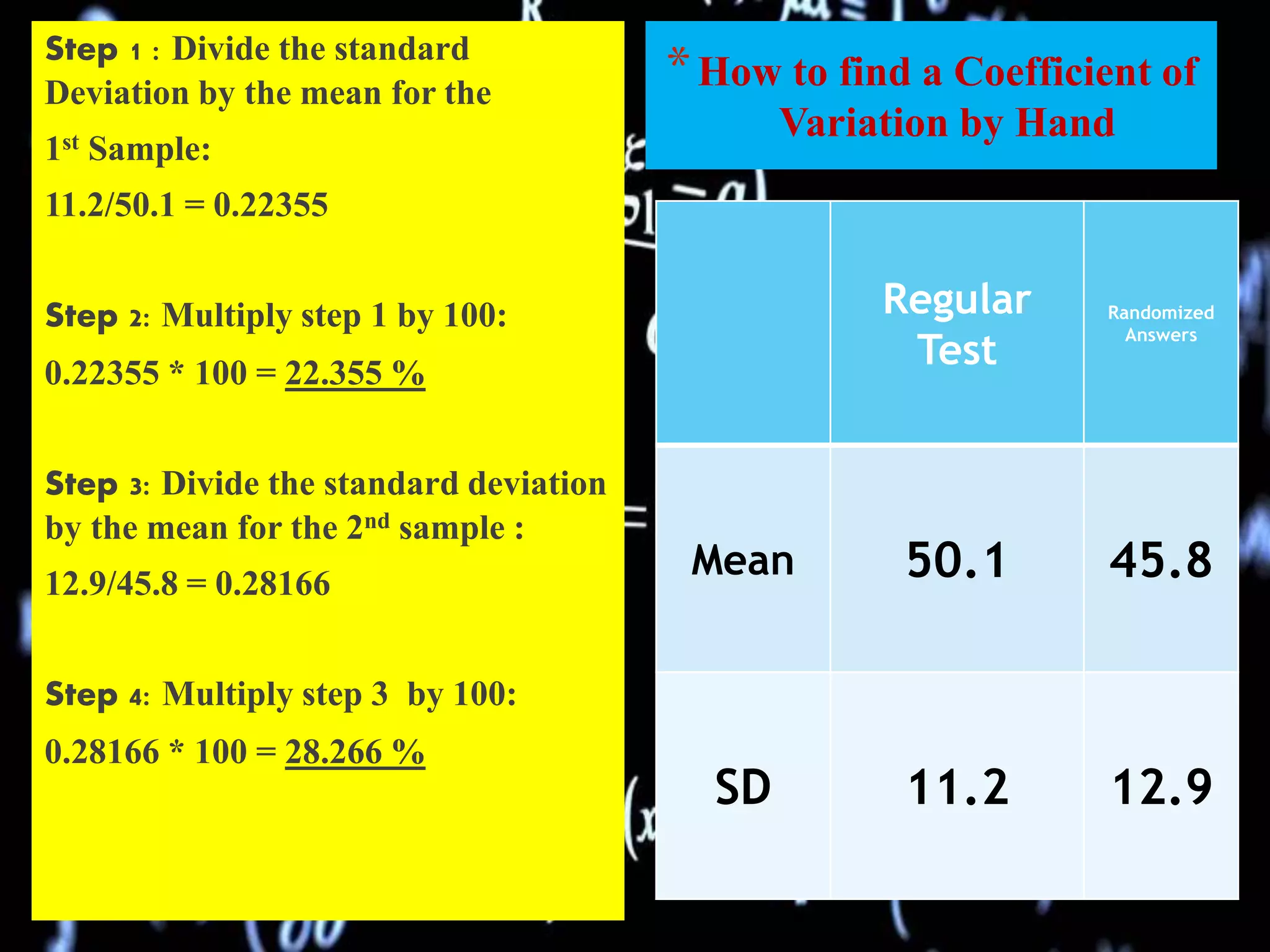
The document discusses coefficient of variation (CV), which is the ratio of the standard deviation to the mean. It provides an example comparing the CV of two multiple choice tests with different conditions. Formulas for calculating CV by hand and in Excel are shown. Methods for finding quartiles in ungrouped and grouped data are explained. The document also demonstrates how to calculate quartile deviation and construct box and whisker plots, and provides references for further information.

2.  What is Coefficient of Variation?
 What are the Formulas of COV in
Excel
 How to find COV by Hand
 Calculating Quartile (Ungrouped
Data)
 Calculating Quartile
(Group Data)
 Calculating COV by Box and
Whisker Plot
 References
*

4. The Coefficient of Variation (CV) also
known as Relative Standard Deviation
(RSD) is the ratio of the standard
deviation(σ) to the mean (μ).
*

6. Regular
Test
Randomized
Answers
Mean 59.9 44.8
SD 10.2 12.7
* For Example …
A researcher is comparing two multiple choice test
with different conditions. In the first test, a typical
multiple – choice test is administered. In the second
test, alternative choices are randomly assigned to
test takers. The results from the two test are:

7. *
Regular
Test
Randomized Answers
Mean 59.9 44.8
SD 10.2 12.7
CV 17.03 28.35

8. *
Excel.xlsx

9. *How to find a Coefficient of
Variation by Hand
Regular
Test
Randomized
Answers
Mean 50.1 45.8
SD 11.2 12.9
Step 1 : Divide the standard
Deviation by the mean for the
1st Sample:
11.2/50.1 = 0.22355
Step 2: Multiply step 1 by 100:
0.22355 * 100 = 22.355 %
Step 3: Divide the standard deviation
by the mean for the 2nd sample :
12.9/45.8 = 0.28166
Step 4: Multiply step 3 by 100:
0.28166 * 100 = 28.266 %

10. *

11. *

13. *Quartiles Raw
or
Ungrouped Data

14. 25, 18, 30, 8, 15, 5,10, 35, 40, 45
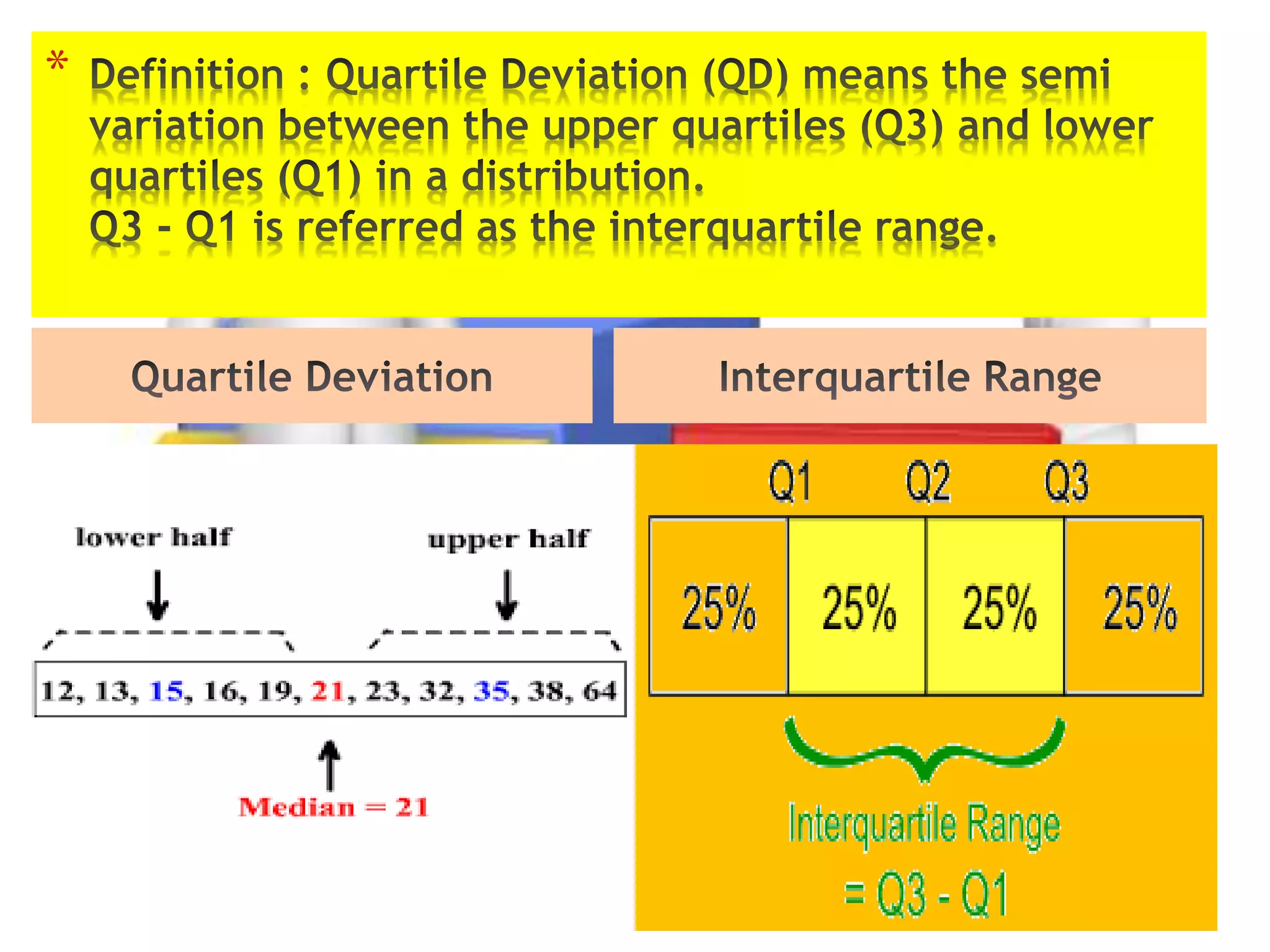
5, 8, 10, 15, 18, 25, 30, 35, 40, 45
𝑄
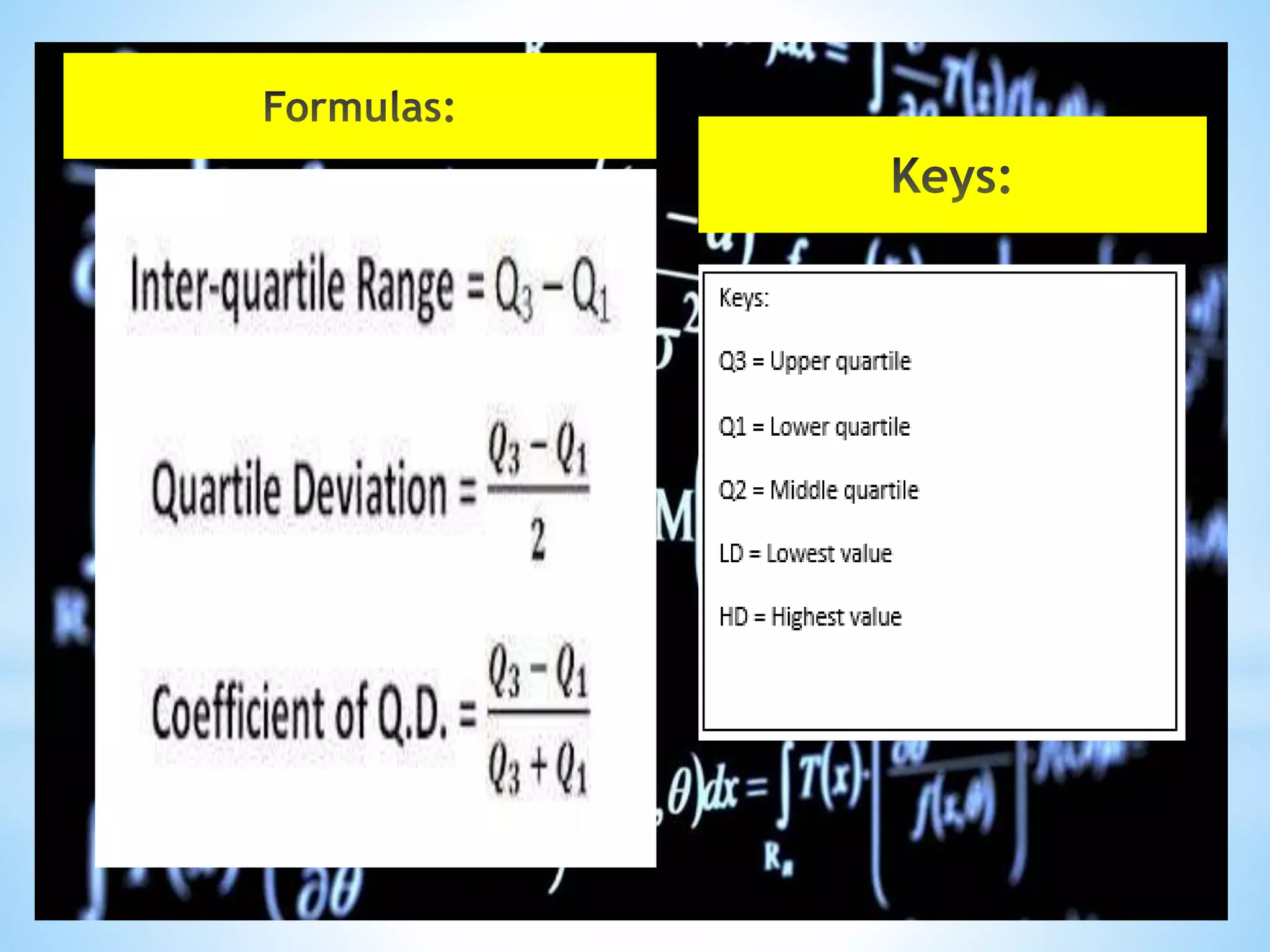
1= (
𝑁+1
4
)
th Item
= (
10+1
4
) th Item
= (2. 75) th Item
= 2nd Item + (
3
4
) (3rd – 2nd )
8 +
3
4
(10 − 8 )
8 +
3
4
x 2
= 8+ 1.5
= 9.5
* 𝑄3 =3 (
𝑁+1
4
)
th Item
*=3 x (2.75) th item
*(8.25) th item
*8th item + (
1
4
) [ 9th – 8th ]
*= 35 +
1
4
[ 40 – 35 ]
*=35 + 1.25
*=36.25

15. *Quartile
Deviation
(Grouped Data)

16. EXAMPLE:
Calculate the
QD for a group of data
Given Data…
241, 521, 421, 250, 300, 365,
840, 958.

17. STEP 1:
First, arrange the given
digits in ascending
order
= 241, 250, 300, 365,
421, 521, 840, 958.
*Total number of given
data (n) = 8.
STEP 2:
Calculate the center value
(n/2) for the given data
{241, 250, 300, 365, 421,
521, 840, 958}.
n=8
n/2 = 8/2
n/2 = 4.
From the given data,
{ 241, 250, 300, 365, 421,
521, 840, 958 }
the fourth value is 365

18. STEP 3:
Now, find out the n/2+1 value.
i.e n/2 +1 = 4+1= 5
From the given data,
{ 241, 250, 300, 365, 421,
521, 840, 958 }
the fifth value is 421
STEP 4:
From the given group of data
{ 241, 250, 300, 365,
421, 521, 840, 958 }
Consider,
*First four values
Q1 = 241, 250, 300, 365
*Last four values
Q3 = 421, 521, 840, 958

19. STEP 5:
Now, let us find the median value for
Q1.
Q1= {241,250,300,365}
For Q1, total count (n) = 4
Q1(n/2) = Q1(4/2) = Q1(2)
i.e) Second value in Q1 is 250
Q1( (n/2)+1 ) = Q1( (4/2)+1 )
= Q1(2+1)
= Q1(3)
i.e) Third value in Q1 is 300
Median (Q1) = ( Q1(n/2) +
Q1((n/2)+1) ) / 2
(Q1) = 250+300/2
(Q1) = 550/2 = 275
* STEP 6:
Let us now calculate the median value
for Q3.
Q3= {421, 521, 840, 958}
For Q3, total count (n) = 4
Q3(n/2) = Q3(4/2) = Q3(2)
i.e) Second value in Q3 is 521
Q3( (n/2)+1 ) = Q3( (4/2)+1 )
= Q3(2+1)
= Q3(3)
i.e) Third value in Q3 is 840.
Median (Q3) = ( Q1(n/2) + Q1((n/2)+1) )
/ 2
(Q3) = ( 521 + 840 ) / 2
(Q3) = 1361/2 = 680.5

20. *Step 7:
Now, find the median value between
Q3 and Q1.
Quartile Deviation = Q3-Q1/2
= 680.5 - 275/2
= 202.75

21. *Box and Whisker Plot

22. { 3, 7, 7, 3, 10, 1, 6, 6 }
1, 3 I 3, 6 I 6, 7 I 7, 10
*Min : 1
*Max: 10
*Median: 6
*Q1: 3
*Q3: 7
*IQR: 4
{ 3, 10, 2, 8, 7, 5, 2, 5 }
2, 2 I 3, 5 I 5, 7 I 8, 10
*Min: 2
*Max: 10
*Median: 5
*Q1: 2.5
*Q3: 7.5
*IQR: 5
*

23. *
*http://www.lexic.us/definition-of/quartile
*https://www.google.com.ph/search?q=QUARTILE+DEVIATION++FORMULA&bi
w=1093&bih=471&source=lnms&tbm=isch&sa=X&ved=0ahUKEwjqhanq7IHSA
hVEn5QKHW39BFcQ_AUIBigB#tbm=isch&q=box+and+whisky+plots
*http://www.purplemath.com/modules/boxwhisk.htm
*https://www.youtube.com/watch?v=FQqUmWPpI_M
*https://www.youtube.com/watch?v=ybHABoAlIQE

24. *“All the statistics in the
world can't measure the
warmth of a smile.”
― Chris Hart

25. ROSELYN 