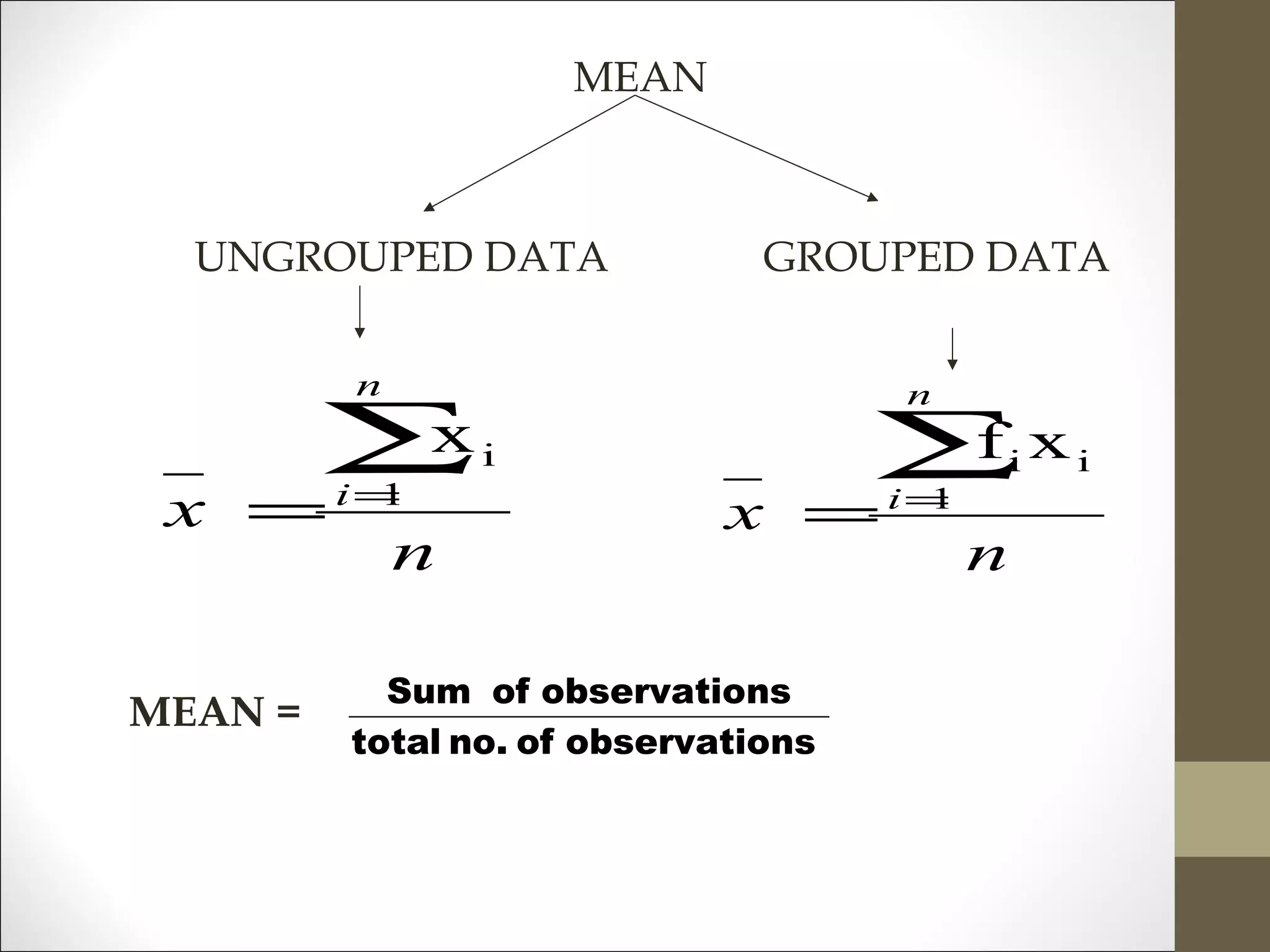
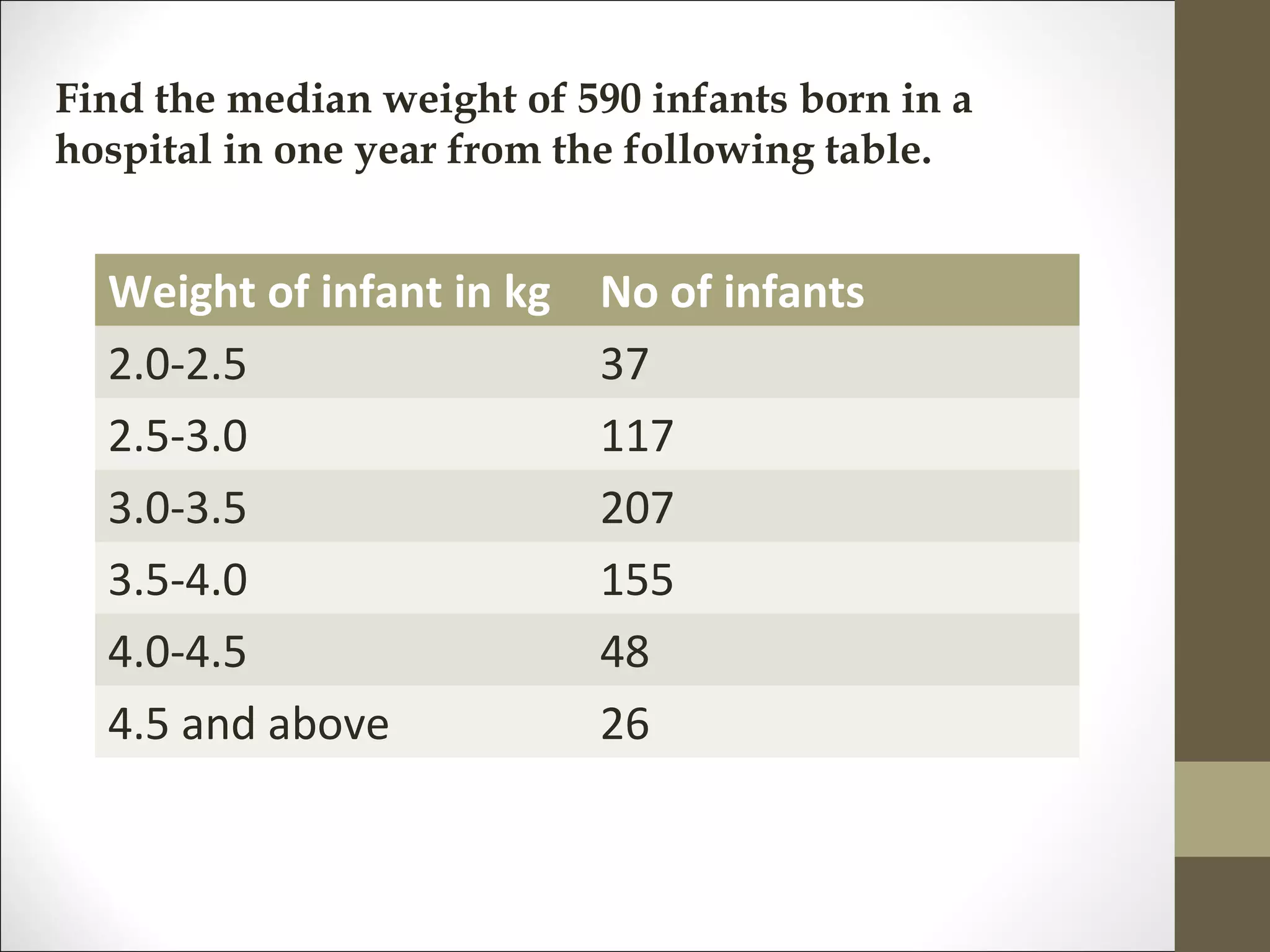
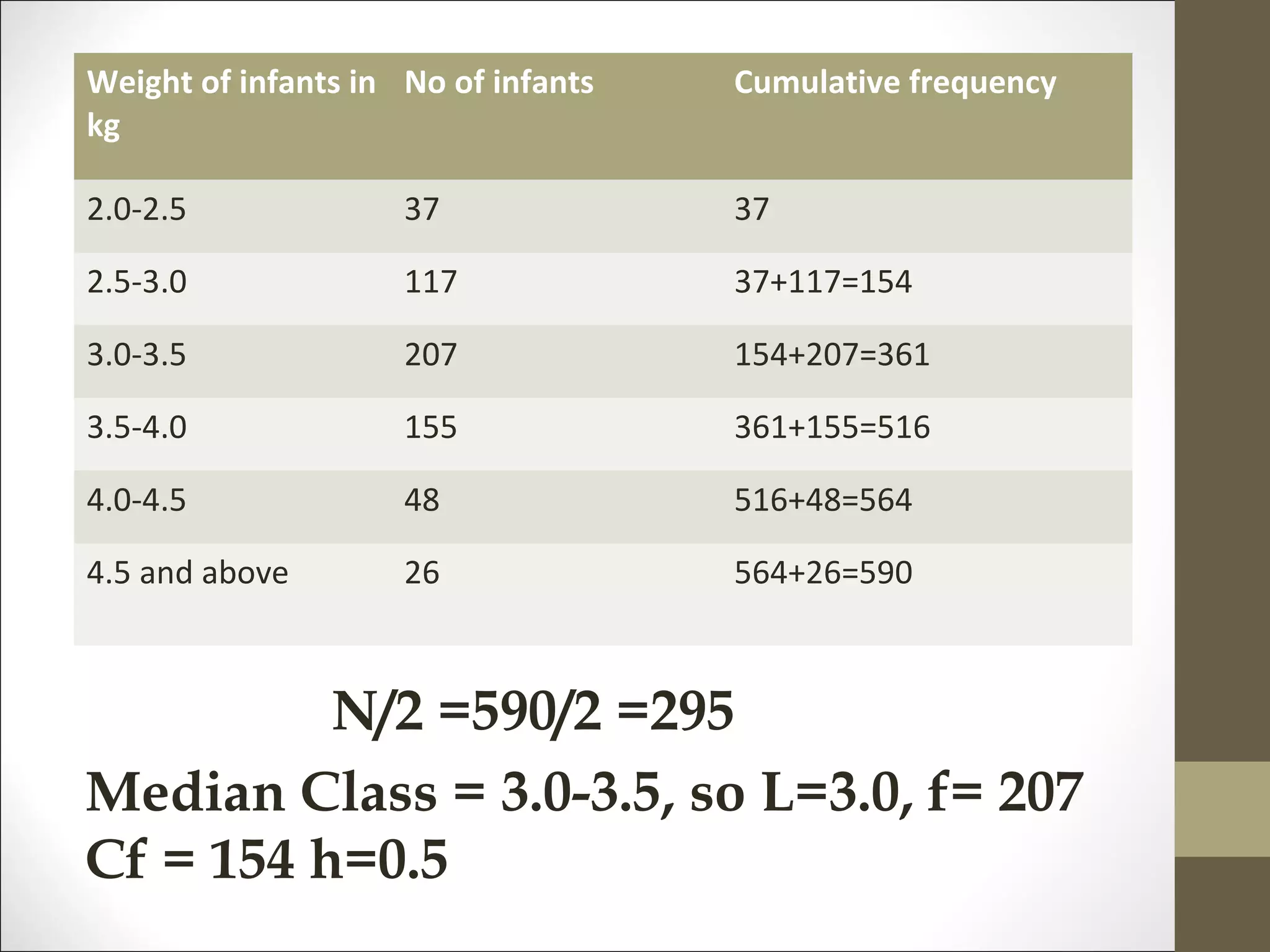
The document discusses measures of central tendency, identifying five main types: arithmetic mean, median, mode, geometric mean, and harmonic mean. Each measure is described with its merits and demerits, alongside calculation methods and examples to illustrate their applications. The document emphasizes how these measures provide insights into value concentration within data distributions.

1. Measures of
Central Tendency
Harshit Jadav
M.S.Pharm, PGDRA

2. • Measures of central tendency are also usually
called as the averages.
• They give us an idea about the concentration
of the values in the central part of the
distribution.
• The following are the five measures of
central tendency that are in common use:
• (i) Arithmetic mean, (ii) Median, (iii) Mode,
(iv) Geometric mean, and (v) Harmonic mean
(vi) weighted mean

3. MEASURE OF CENTRAL TENDANCY
MEAN
MEDIAN MODE
The average of the data
The middle value of the
data
most commonly
occurring value

4. Mean (Average)
Mean locate the centre of distribution.
Also known as arithmetic mean
Most Common Measure
The mean is simply the sum of the values divided by
the total number of items in the set.
Affected by Extreme Values
XX
XX
nn
XX XX XX
nn
ii
ii
nn
nn
== ==
++ ++ ++==
∑∑
11 11 22 

5. Merits:
• It is easy to understand and easy to calculate
• It is based upon all the observations
• It is familiar to common man and rigidly
defined
• It is capable of further mathematical
treatment.
• It is affected by sampling fluctuations. Hence
it is more stable.

6. Demerits
• It cannot be determined by inspection.
• Arithmetic mean cannot be used if we are
dealing with qualitative characteristics,
which cannot be measured quantitatively
like caste, religion, sex.
• Arithmetic mean cannot be obtained if a
single observation is missing or lost
• Arithmetic mean is very much affected by
extreme values.

7. MEAN
UNGROUPED DATA GROUPED DATA
n
x
n
i
∑=
= 1
ix
n
x
n
i
∑=
= 1
ii xf
MEAN =
nsobservatioofno.total
nsobservatioofSum

8. Birth weight of new borns are :
3.3, 6.1, 5.8, 3.8, 2.7, 4.1, 3.4, 3.9, 5.1, 3
n
x
n
i
∑=
= 1
ix =41.2/10
=4.12 kg

9. Q. A Survey of 100 families each having five children,
revealed the following distribution
No. of male children 0, 1, 2, 3, 4, 5
No. of Families 9, 24, 35, 24, 6, 2
Find the Mean of male children.
x f f . X
0 9 0
1 24 24
2 35 70
3 24 72
4 6 24
5 2 10
N=100 Σ f.x = 200
Mean = X =Σ f.x / Σf
X =200/ 100 = 2

10. Find mean days of confinement after
delivery in the following series:-
Day of
confinement
No. of
patients
6 5
7 4
8 4
9 3
10 2

11. Day of
confinement
(x)
No. of
patients
(f)
X*f
6 5 30
7 4 28
8 4 32
9 3 27
10 2 20
Total 18 137
Solution:-
n
x
n
i
∑=
= 1
ii xf =137/18
=7.61

12. Median
1.Measure of Central Tendency.
2. The median is determined by sorting the data set
from lowest to highest values and taking the data
point in the middle of the sequence.
3.Middle Value In Ordered Sequence
• If Odd n, Middle Value of Sequence
• If Even n, Average of 2 Middle Value
4.Not Affected by Extreme Values

13. Merits:
• It is rigidly defined
• It is easy to understand and easy to
calculate.
• It is not at all affected by extreme values.
• It can be calculated for distributions with
open-end classes.
• Median is the only average to be used
while dealing with qualitative data.
• Can be determined graphically.

14. Demerits:
• In case of even number of observations
median cannot be determined exactly.
• It is not based on all the observations.
• It is not capable of further mathematical
treatment

15. For ungrouped data:-
Step-1
Arranged data in ascending or descending order.
Step:-2
If total no. of observations ‘n’ is odd then used the
following formula for median
Step:-3
If total no. of observations ‘n’ is even then used
the following formula for
median = arithmetic mean of two middle
observations.
.
2
1
nobservatioth
n +
=

16. Median
If X1, X2, X3,... …. ,Xn are n observations
arranged in ascending order of magnitude.
X(n+1)/2 if n is odd
Median = {
Xn/2 + X(n/2)+1 if n is even
------------------
2

17. Calculate the median for the following
series :-
2,3,5,1,4,5,8
1,2,3,4,5,5,8.
Median .
2
1
nobservatioth
n +
=
= 7+1/2
=4th
number

18. 74+75
Median = ---------- = 74.5
2
The data on pulse rate per minute of 10 healthy
individuals are 82, 79, 60, 76, 63,81, 68, 74, 60, 75.
n= 10
60, 60, 63, 68, 74,75, 76, 79, 81, 82
Xn/2 + X(n/2)+1 / 2

19. Find out the median for number of
sports injuries happened in cricket in all teams
37, 57, 65, 46, 12, 14, 19, 23, 56, 78, 5, 33

20. Median:-
f
hc
n
l






−
+
2
l = lower limit of class interval where the
median occurs
f = Frequency of the class where median occurs
h = Width of the median class
C= Cumulative frequency of the class
preceding the median class (PCF)
For Grouped data:-

21. Weight of infant in kg No of infants
2.0-2.5 37
2.5-3.0 117
3.0-3.5 207
3.5-4.0 155
4.0-4.5 48
4.5 and above 26
Find the median weight of 590 infants born in a
hospital in one year from the following table.

22. Weight of infants in
kg
No of infants Cumulative frequency
2.0-2.5 37 37
2.5-3.0 117 37+117=154
3.0-3.5 207 154+207=361
3.5-4.0 155 361+155=516
4.0-4.5 48 516+48=564
4.5 and above 26 564+26=590
N/2 =590/2 =295
Median Class = 3.0-3.5, so L=3.0, f= 207
Cf = 154 h=0.5

23. f
hc
n
l






−
+
2
= 3.0 + (295-154) * 0.5
207
= 3.0 + 0.34
= 3.34 Median Weight

24. For grouped Data:-
Class interval Frequency
5-9 2
10-14 11
15-19 26
20-24 17
25-29 8
30-34 6
35-39 3
40-44 2
45-49 1
Calculate the median for the following data
series:-

25. Solution:-
Class interval
Frequency
cumulative
frequency
5-9 2 2
10-14 11 13
15-19 26 39
20-24 17 56
25-29 8 64
30-34 6 70
35-39 3 73
40-44 2 75
45-49 1 76

26. n=76
l = lower limit of class interval where the median
occurs
= 15
h = Width of the median class
= 4
f = Frequency of the class where median occurs
= 26
C = Cumulative frequency of the class
preceding the median class
=13
f
hc
n
l






−
+
2

27. Mode
1.Measure of Central Tendency
2.The mode is the most frequently
occurring value in the data set.
3.May Be No Mode or Several Modes

28. Merits:
• Mode is readily comprehensible and easy to
calculate.
• Mode is not at all affected by extreme values.
• Mode can be conveniently located even if the
frequency distribution has class intervals of
unequal magnitude
• Open-end classes also do not pose any
problem in the location of mode.
• Mode is the average to be used to find the
ideal size.

29. Demerits:
• Mode is ill defined.
• It is not based upon all the observations.
• It is not capable of further mathematical
treatment.
• As compared with mean, mode is affected
to a great extent by fluctuations of
sampling.

30. Mode Example
No Mode
Raw Data: 10.3 4.9 8.9 11.7 6.3 7.7
One Mode
Raw Data: 6.3 4.9 8.9 6.3 4.9 4.9
More Than 1 Mode
Raw Data: 21 28 28 41 43 43

31. Mode for ungrouped data:-
2,2,3,4,6,7,4,4,4,4,8,9,0 mode is 4
10,10,3,3,4,2,1,6,7 mode is 10 and 3
10,34,23,12,11,3,4 no mode

32. Mode for Group Data
Fm-F1
Mode = L1 + ------------------ * c
2Fm– F1- F2
Where
•Fm is mode freq.
• F1 is freq. just lower mode class.
•F2 is freq. after mode class.
• L1 is lower limit of mode class
•C is class difference.

33. C I FREQU. (F)
20 - 30 3
30 - 40 20
40 - 50 27
50 - 60 15
60 - 70 9
Q. Find the Mode for group data
Age group 20-30 30-40 40-50 50-60 60-70
No. of persons 3 20 27 15 9

34. Q. Find the Mode for group data
Age group 20-30 30-40 40-50 50-60 60-70
No. of persons 3 20 27 15 9
C I FREQU. (F)
20 - 30 3
30 - 40 20
40 - 50 27
50 - 60 15
60 - 70 9
L1
Fm
F1
F2

35. FFmm -- FF11
Mode = LMode = L11 + ------------------ * c+ ------------------ * c
2F2Fmm – F– F11- F- F22
2727 –– 20 7020 70
Mode = 40 + ------------------ * 10 = 40 + -----Mode = 40 + ------------------ * 10 = 40 + -----
2*272*27 – 20- 15 19– 20- 15 19
Mode = 43.68Mode = 43.68

36. Calculate the mode for the following
frequency distribution:-
IQ Range Frequency
90-100 11
100-110 27
110-120 36
120-130 38
130-140 43
140-150 28
150-160 16
160-170 1

37. Modal class by inspection is
130-140
fm= 43
f1= 38
f2= 28
C=10
l = 130
c
fff
ff
l
m
m






−−
−
+
)(2
)(
21
1
=130.6579

38. Relationship between
Mean, Median and Mode
Mode = 3 Median – 2 Mean

39. Summary of
Central Tendency Measures
MeasureMeasure DescriptionDescription
MeanMean Balance PointBalance Point
MedianMedian Middle ValueMiddle Value
When OrderedWhen Ordered
ModeMode Most FrequentMost Frequent

40. Ex. Calculate Mean, Median, Mode.
Age Group
No. of
Patients
25-30 4
30-35 3
35-40 2
40-45 3
45-50 4
50-55 8
55-60 6

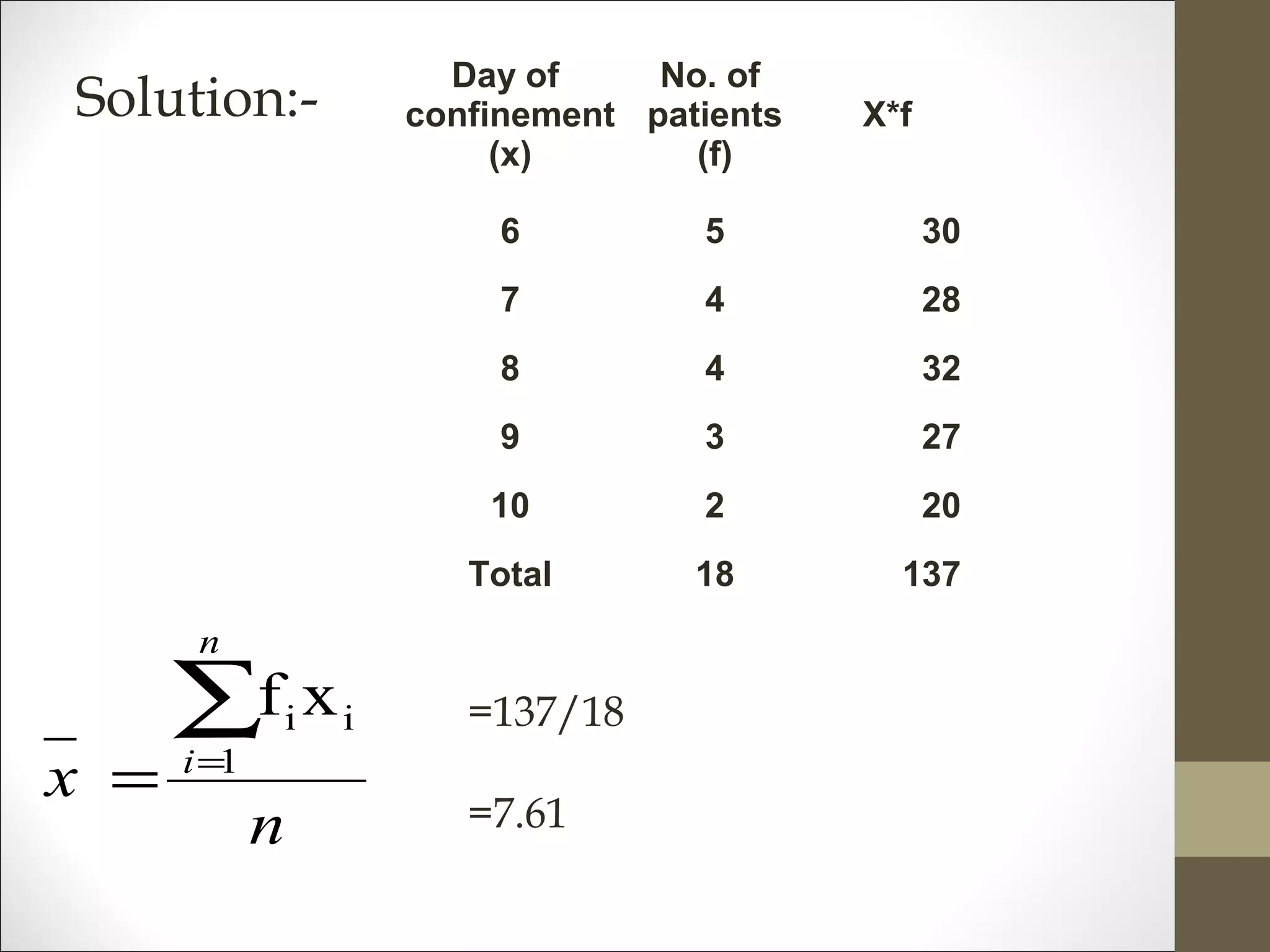
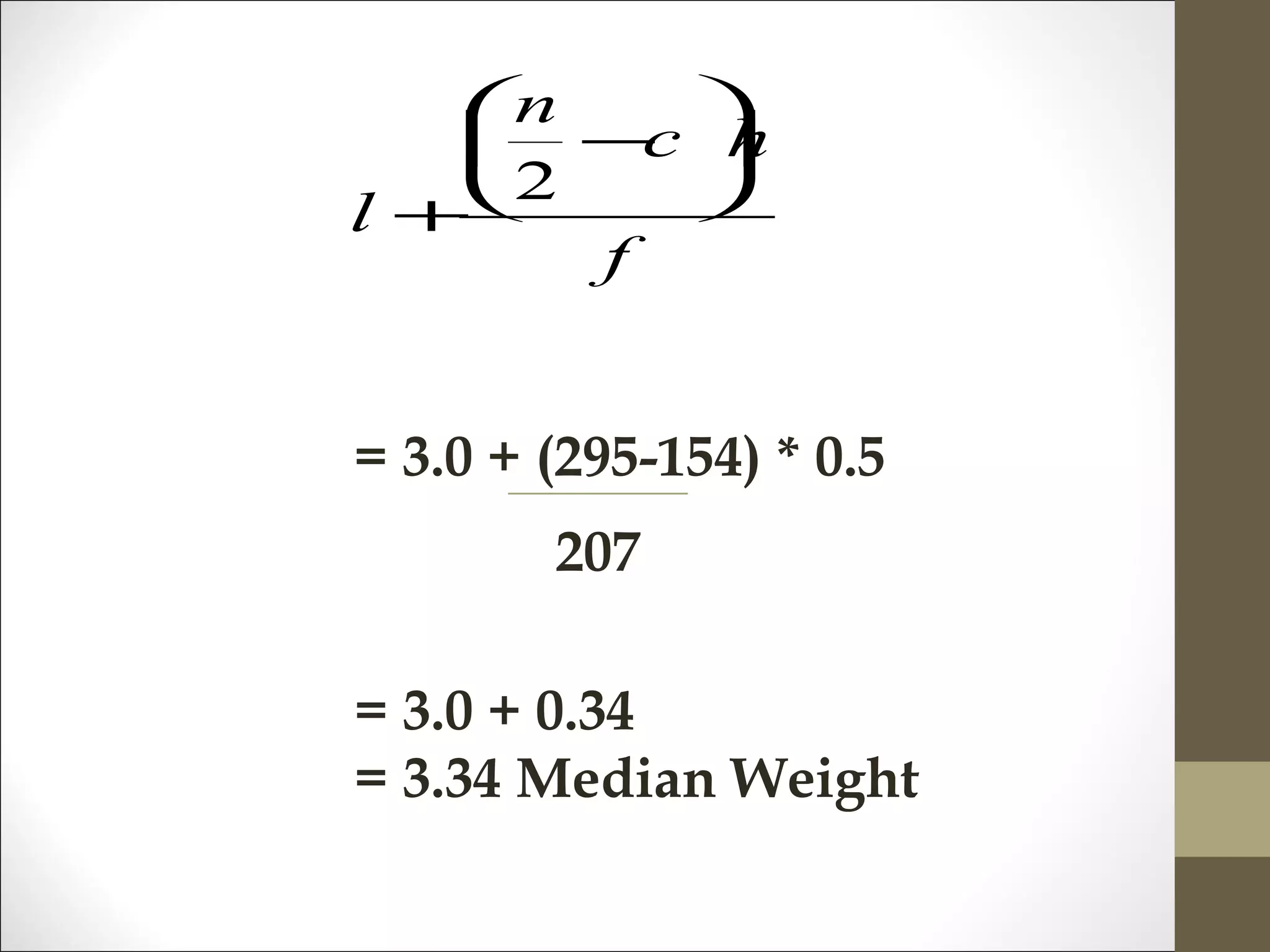
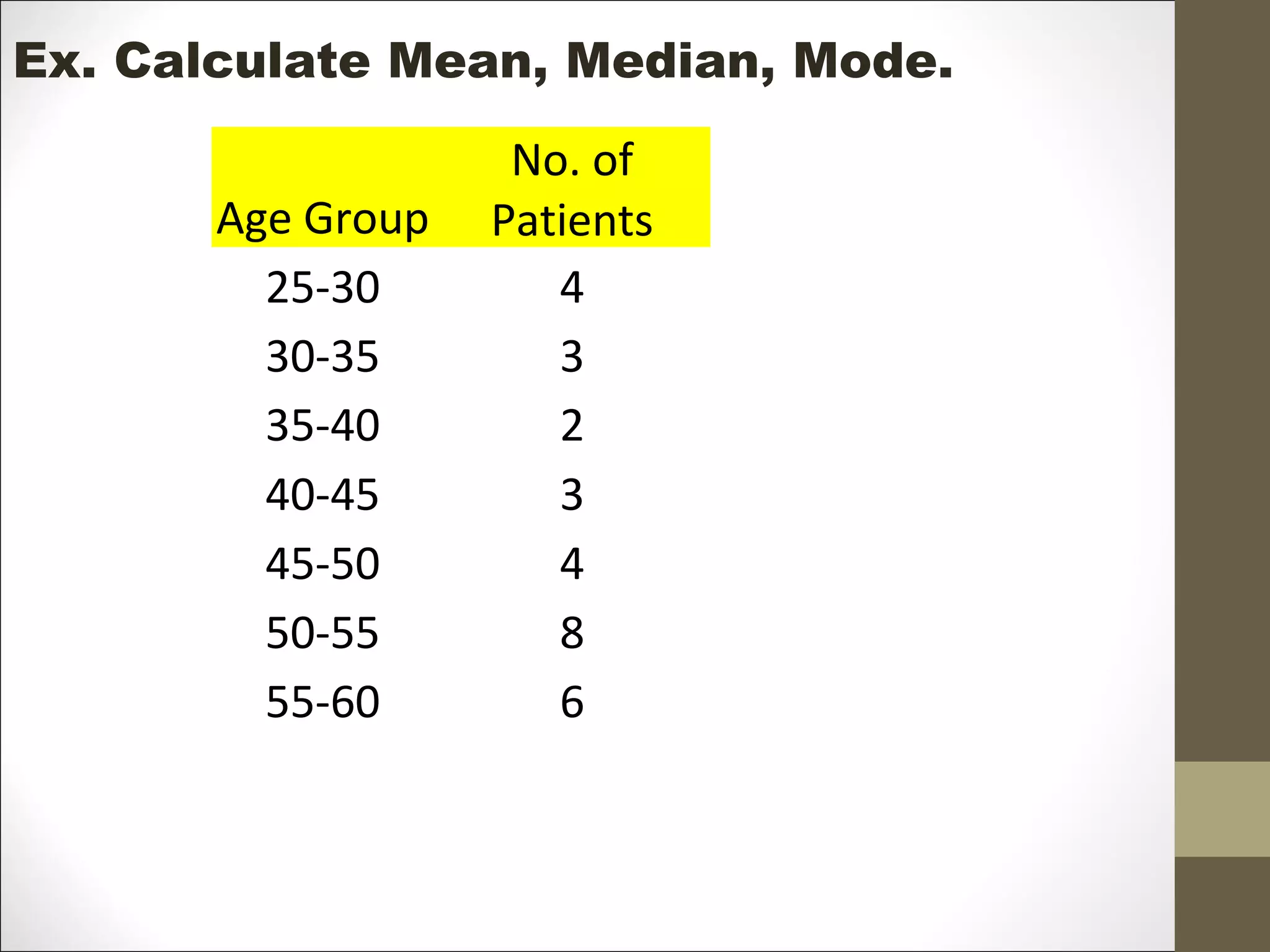
41. Age Group No. of Patients (F) X F*X C.F
25-30 4 27.5 110 4
30-35 3 32.5 97.5 7
35-40 2 37.5 75 9
40-45 3 42.5 127.5 12
45-50 4 47.5 190 16
50-55 8 52.5 420 24
55-60 6 57.5 345 30
30 1365
MEAN =1365/30 = 45.5
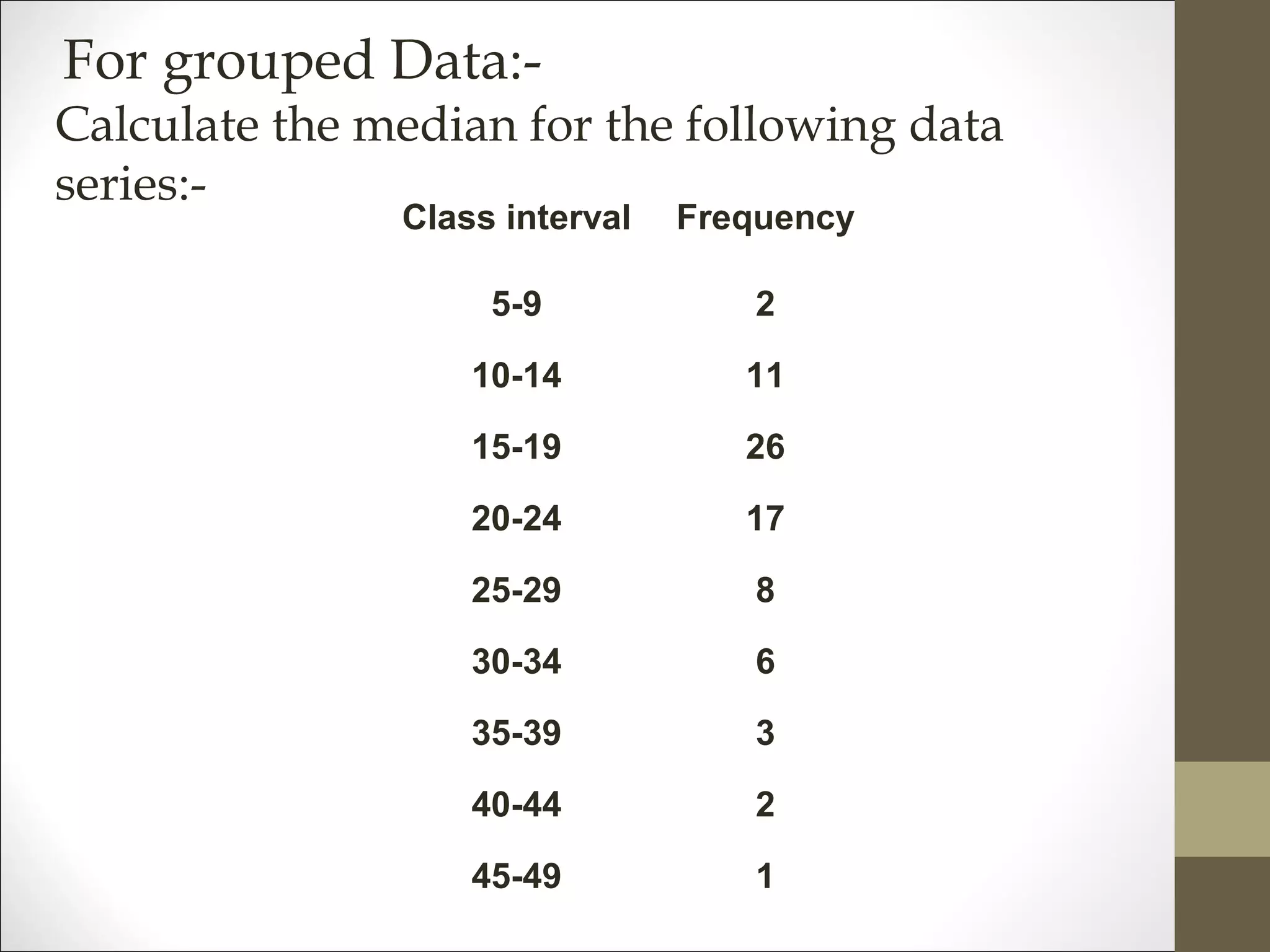
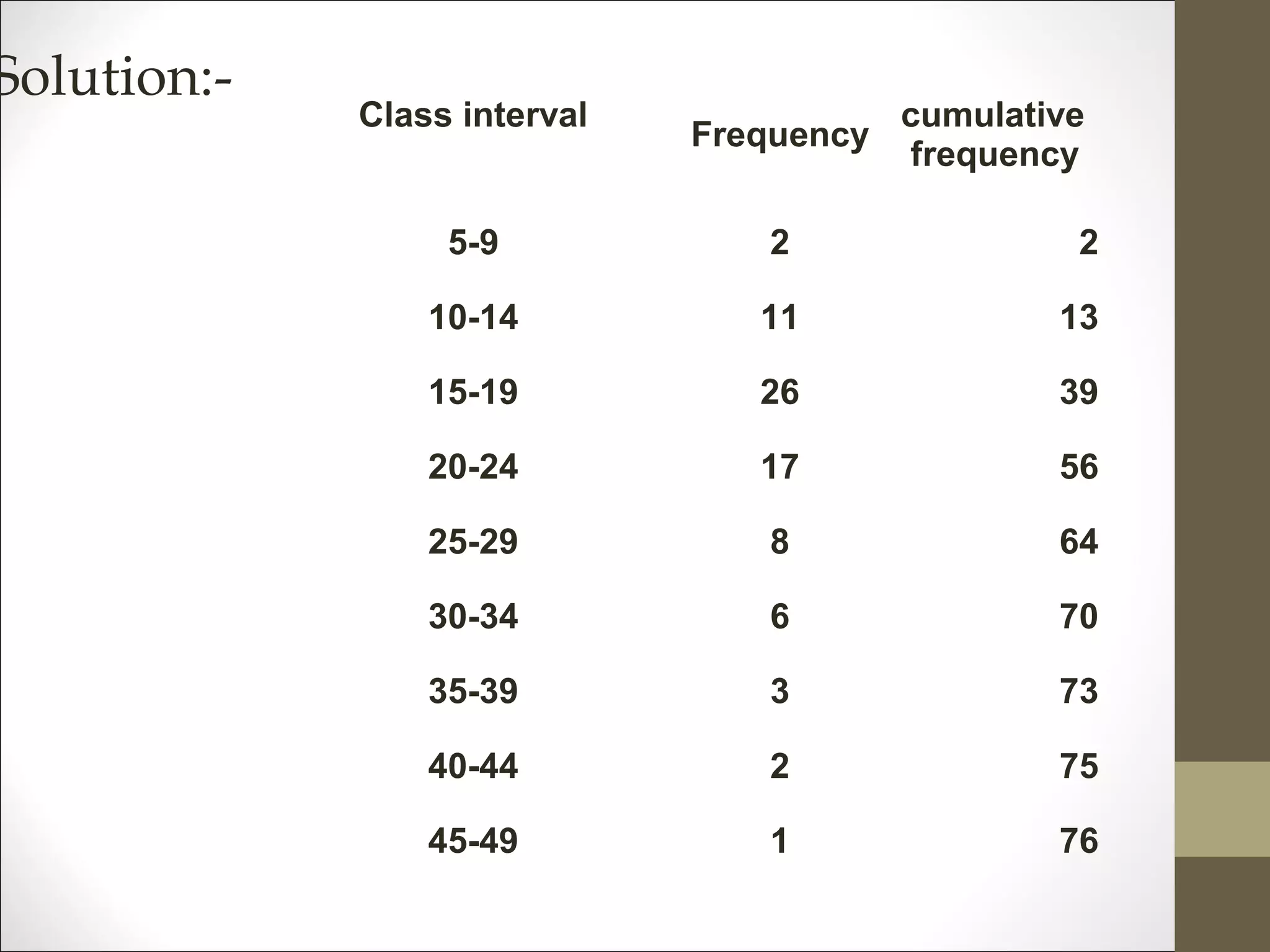
MEDIAN =45+ (15-12)*5/4 = 48.75
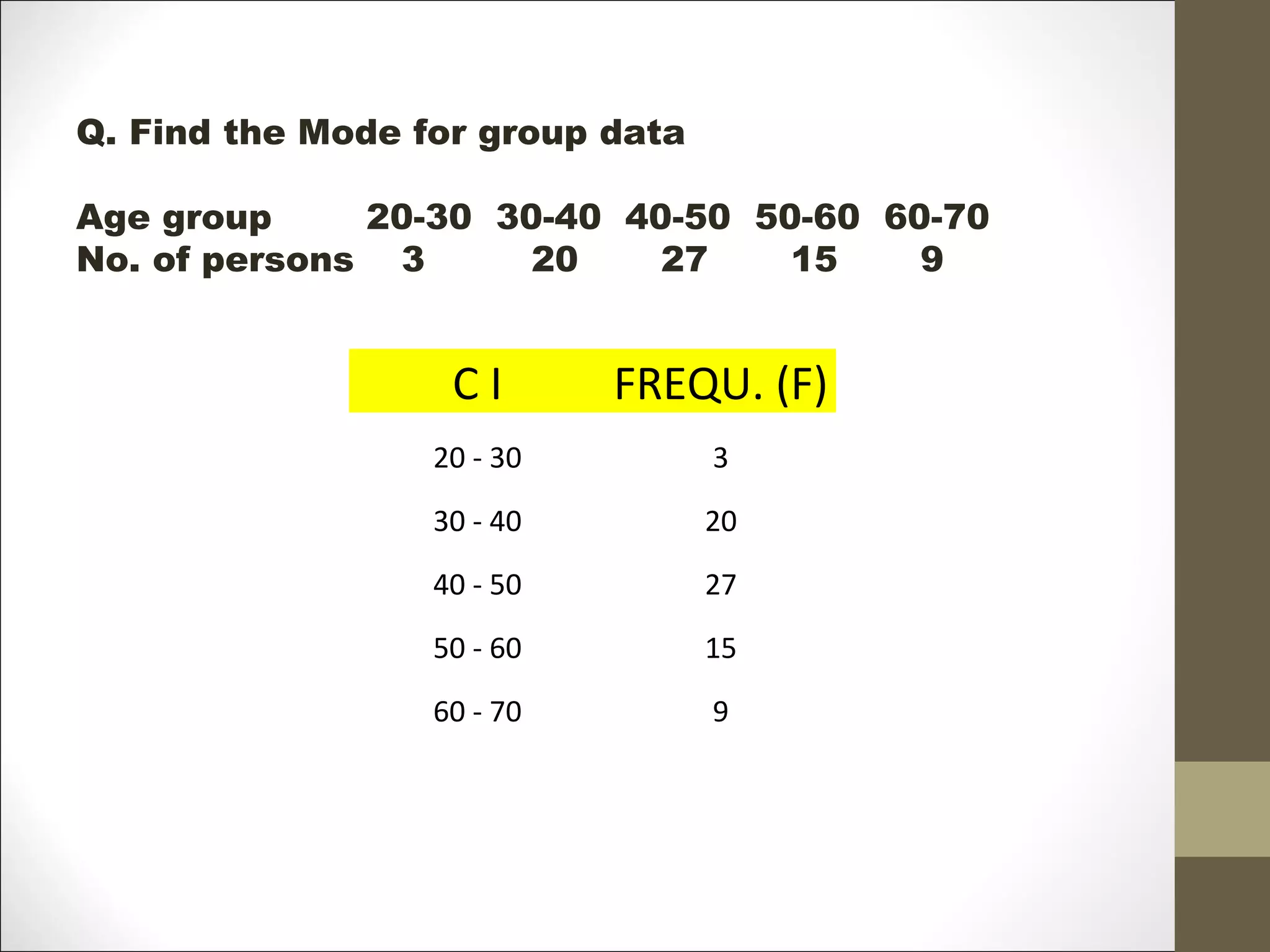
MODE=50 + [(8-4)*5/(2*8-4-6)]=53.34

42. Ex. The following table gives the frequency
distribution of marks obtained by 2300 medical
students of Gujarat in MCQ of PSM exam. Find
Mean, Median and Mode.
Marks
No. of
students
11-20 141
21-30 221
31-40 439
41-50 529
51-60 495
61-70 322
71-80 153

43. Geometric Mean
• Geometric mean is defined as the positive root of the
product of observations. Symbolically,
• It is also often used for a set of numbers whose values are
meant to be multiplied together or are exponential in nature,
such as data on the growth of the human population or
interest rates of a financial investment.
• Find geometric mean of rate of growth: 34, 27, 45, 55, 22, 34
n
nxxxxG /1
321 )( =

44. Geometric mean of Group
data
• If the “n” non-zero and positive variate-values occur
times, respectively, then the geometric mean of the
set of observations is defined by:
[ ] Nn
i
f
i
Nf
n
ff in
xxxxG
1
1
1
21
21






== ∏=

∑=
=
n
i
ifN
1
Where
nxxx ,........,, 21 nfff ,.......,, 21

45. Geometric Mean (Revised Eqn.)
)( 321 nxxxxG =








= ∑=
n
i
ixLog
N
AntiLogG
1
1








= ∑=
n
i
ii xLogf
N
AntiLogG
1
1
)( 321
321 n
fff
xxxxG =
Ungroup Data Group Data

47. What is the geometric mean of 4,8.3,9
and 17?

48. First, multiply the numbers together
and then take the 5th root (because
there are 5 numbers)
G = (4*8*3*9*17)(1/5)
G = 6.81

49. Harmonic Mean
• Harmonic mean (formerly sometimes called the
subcontrary mean) is one of several kinds of
average.
• The harmonic mean is a very specific type of
average.
• It’s generally used when dealing with averages of
units, like speed or other rates and ratios.

50. Harmonic Mean Group Data
• The harmonic mean H of the positive real numbers x1,x2, ..., xn
is defined to be
∑=
= n
i i
i
x
f
n
H
1
∑=
= n
i ix
n
H
1
1
Ungroup Data Group Data

51. What is the harmonic mean of 1,5,8,10?
Here,
N=4
H = 4 / (1/1) +(1/5) + (1/8) + (1/10)
H = 4/ 1.425
H = 2.80
∑=
= n
i ix
n
H
1
1

52. Rahul drives a car at 20 mph for the
first hour and 30 mph for the second.
What’s his average speed?

53. We need the harmonic
mean:
= 2/(1/20 + 1/30)
= 2(0.05 + 0.033)
= 2 / 0.083
= 24.09624 mph.

54. Weighted Mean
• The Weighted mean of the positive real numbers
x1,x2, ..., xn with their weight w1,w2, ..., wn is defined
to be
∑
∑
=
=
= n
i
i
n
i
ii
w
xw
x
1
1
Σ = the sum of (in other words…add them up!).
w = the weights.
x = the value.

55. A weighted mean is a kind of average.
Instead of each data point contributing
equally to the final mean, some data points
contribute more “weight” than others.
If all the weights are equal, then the
weighted mean equals the arithmetic mean
(the regular “average” you’re used to).
Weighted means are very common in
statistics, especially when studying
populations.

56. Steps:
1.Multiply the numbers in your data set
by the weights.
2.Add the numbers in Step 1 up. Set this
number aside for a moment.
3.Add up all of the weights.
4.Divide the numbers you found in Step 2
by the number you found in Step 3.

57. You take three 100-point exams in your
statistics class and score 80, 80 and 95. The last
exam is much easier than the first two, so your
professor has given it less weight. The weights
for the three exams are:
•Exam 1: 40 % of your grade. (Note: 40% as a
decimal is .4.)
•Exam 2: 40 % of your grade.
•Exam 3: 20 % of your grade

58. 1.Multiply the numbers in your data set
by the weights:
.4(80) = 32
.4(80) = 32
.2(95) = 19
2. Add the numbers up. 32 + 32 + 19 = 83.
3. (0.4+0.4+0.2) = 1
4. 83/1= 83

59. The arithmetic mean is best used when the sum
of the values is significant. For example, your
grade in your statistics class. If you were to get
85 on the first test, 95 on the second test, and 90
on the third test, your average grade would be
90.
Why don't we use the geometric mean
here?
What about the harmonic mean?

60. What if you got a 0 on your first test and
100 on the other two?
The arithmetic mean would give you a
grade of 66.6.
The geometric mean would give you a grade
of 0!!!
The harmonic mean can't even be applied at
all because 1/0 is undefined.