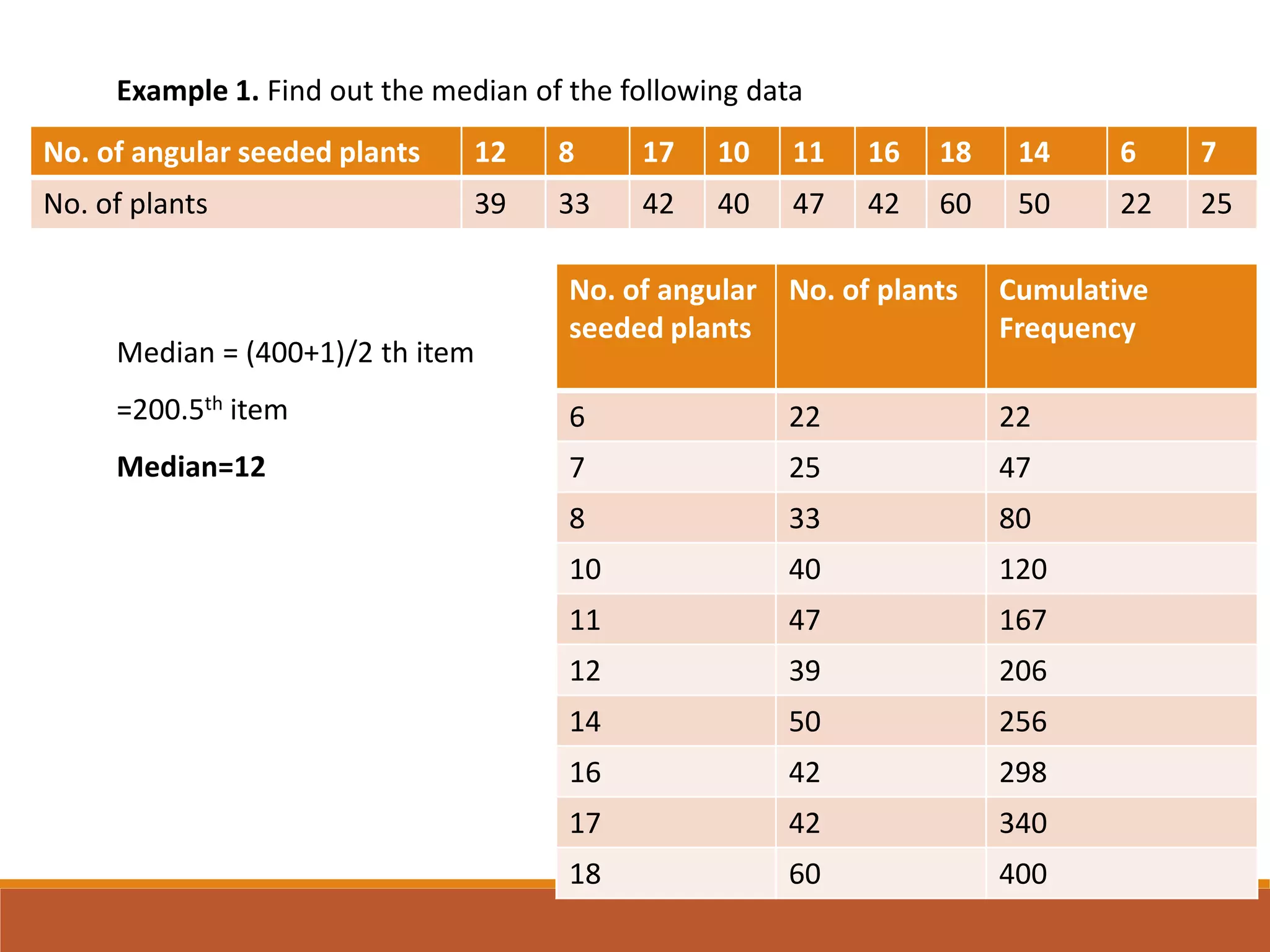
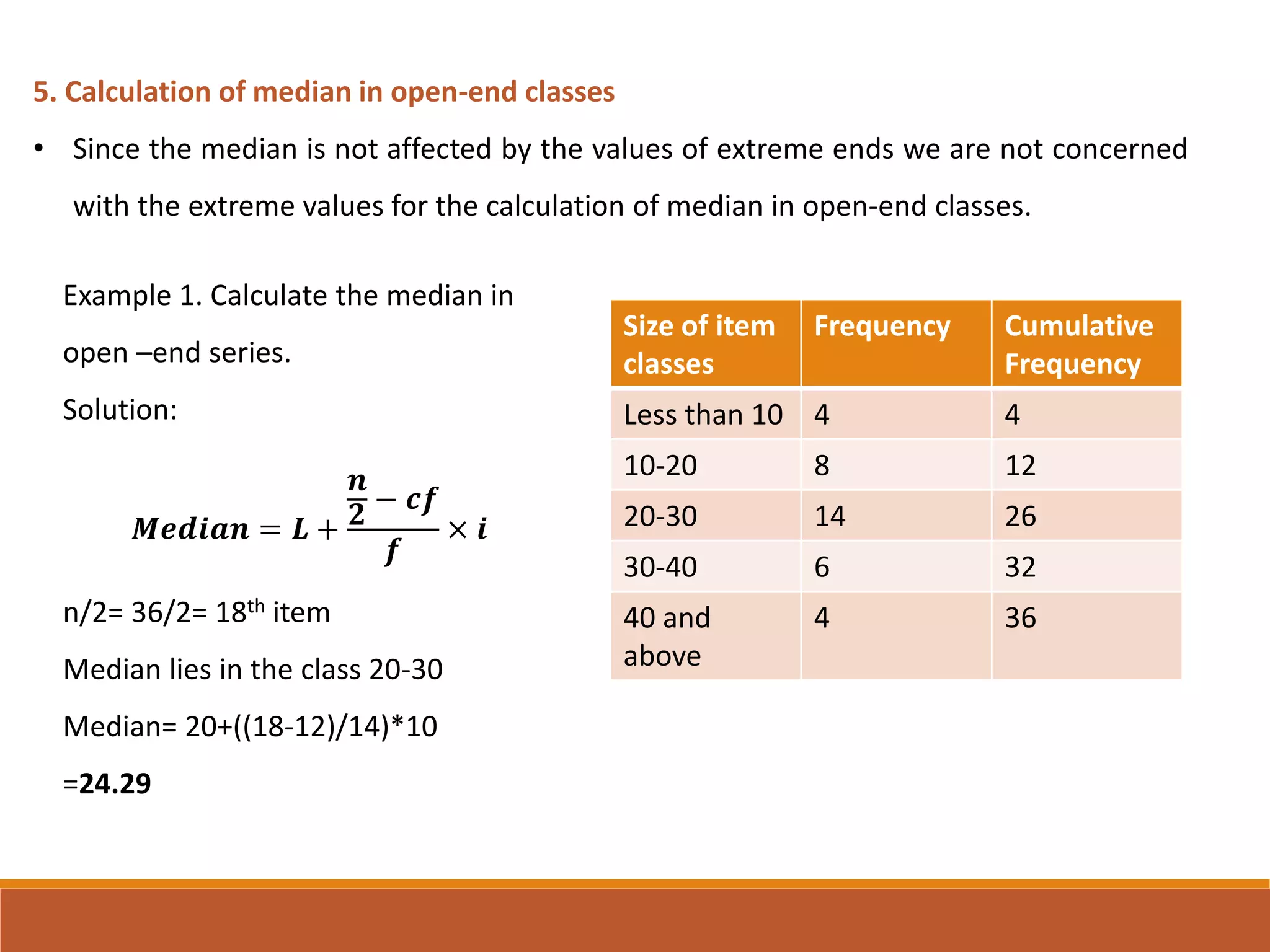
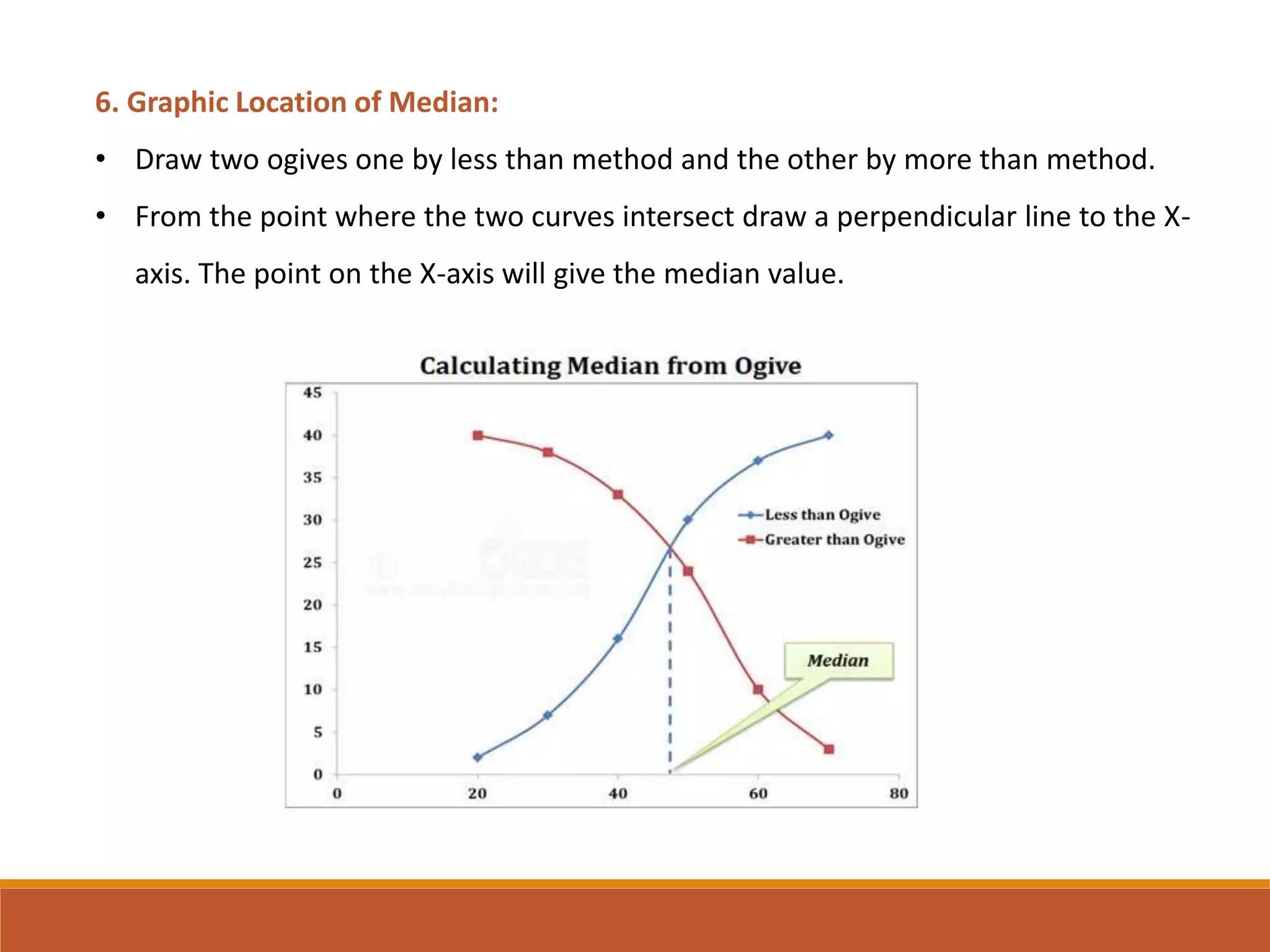
The document outlines the calculation of the median, defining it as the value that divides a distribution into two equal parts. It provides methods for determining the median in individual observations, discrete series, continuous series, unequal class intervals, and open-end classes, including various examples. Additionally, it describes a graphical method for locating the median using ogives.