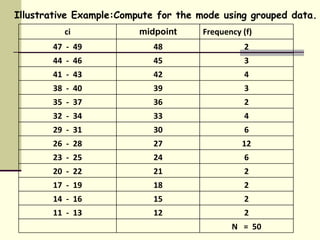
The mode is defined as the score that occurs most frequently in a data set. It is a measure of central tendency that indicates the most common value. For an ungrouped data set, the mode is simply the value that repeats most. For a grouped data set, the mode is calculated using a formula that finds the midpoint of the interval with the highest frequency while accounting for the differences in frequencies on either side of that interval. The mode is useful when wanting a quick approximation of central tendency or when trying to find the most typical value in a data set. Data sets can have one, two, or more modes depending on the number of most frequent values.

1. Mode is defined as the score with the highest frequency. The most frequent score. It is called a nominal statistics. In a grouped data it is the mid point of the class interval with the highest frequency. Characteristics of the Mode 1 . A nominal statistics. 2 . An inspection average. 3. The most frequently occurring score. 4 . Usually occurs near the center of the distribution. 5 . Cannot be obtained by mathematical operations. 6 . The most popular scores. 7 . Some distribution have more than one popular score.

2. When to use the Mode 1. When a quick and approximate measure of central tendency is all that wanted. 2. When the measure of central tendency is the most typical value. Finding the Mode for ungrouped data. Just pick out the most occurring scores. 67, 89, 76, 77, 90, 78, 77, 86, 84, 75 77 is the mode it is called unimodal. A unimodal is as score distribution which contain one mode.

3. 2. 54, 45, 78,34,89, 45, 54 54 and 45 are the mode. It is called bimodal . A bimodal has two most frequent scores occurring. A score with three most frequent score is called trimodal.

4. Finding the Mode for Grouped Data Formula: Mode = where; Mo = mode Ll =lower limit of the class interval with the highest frequency ∆ 1 = highest frequency minus the frequency before the modal class ∆ 2 = highest frequency minus the frequency after the modal class Steps: 1. Prepare a table containing the class interval, frequency . 2. Compute for ∆1 and ∆2. 3. Substitute data to the formula.

5. Illustrative Example:Compute for the mode using grouped data. N = 50 2 12 11 - 13 2 15 14 - 16 2 18 17 - 19 2 21 20 - 22 6 24 23 - 25 12 27 26 - 28 6 30 29 - 31 4 33 32 - 34 2 36 35 - 37 3 39 38 - 40 4 42 41 - 43 3 45 44 - 46 2 48 47 - 49 Frequency (f) midpoint ci

6. Solution: 1. The table reveals that the lower limit of the class interval with the highest frequency is 25.5. 2. Compute for ∆1 and ∆2. ∆ 1 = 12 -6 = 6 ; ∆ 2 = 12 -6 = 6 3. Substitute data to formula = 27

7. Interpretations: The modal class is computed to be 27. This was found to be lower than the computed mean and median which were found to be both 30. This indicate that majority of the students were found below the mean and median.