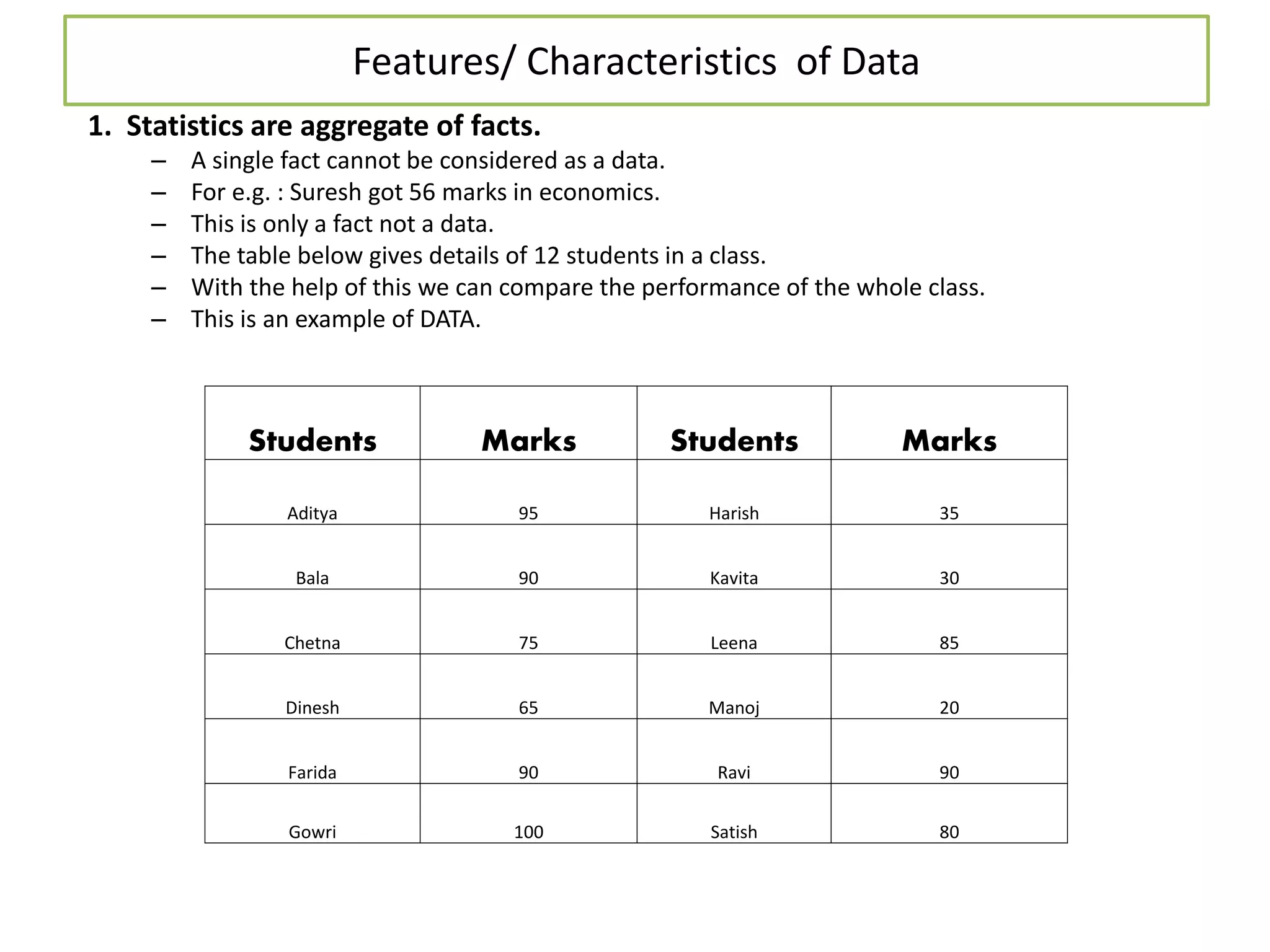
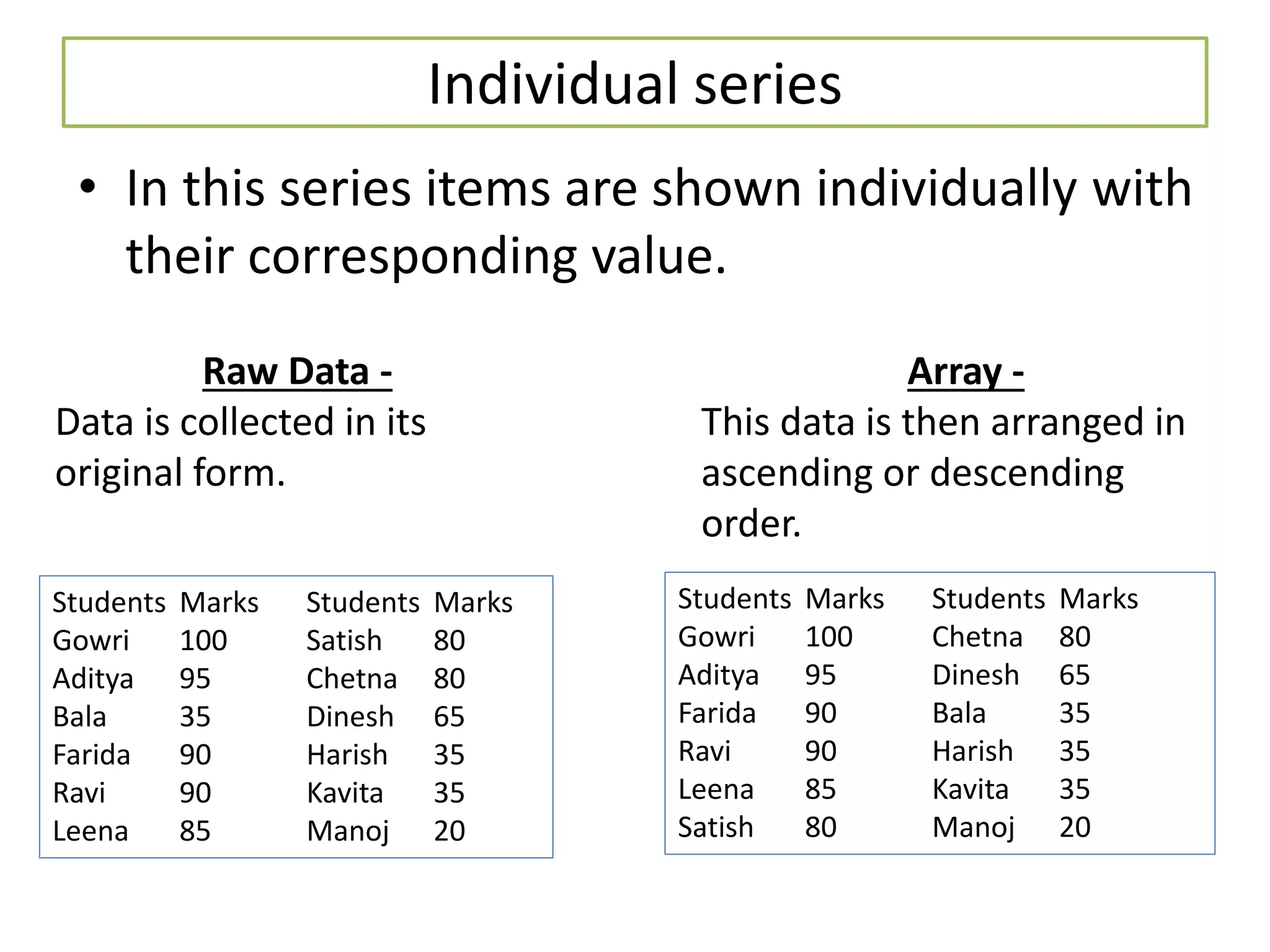
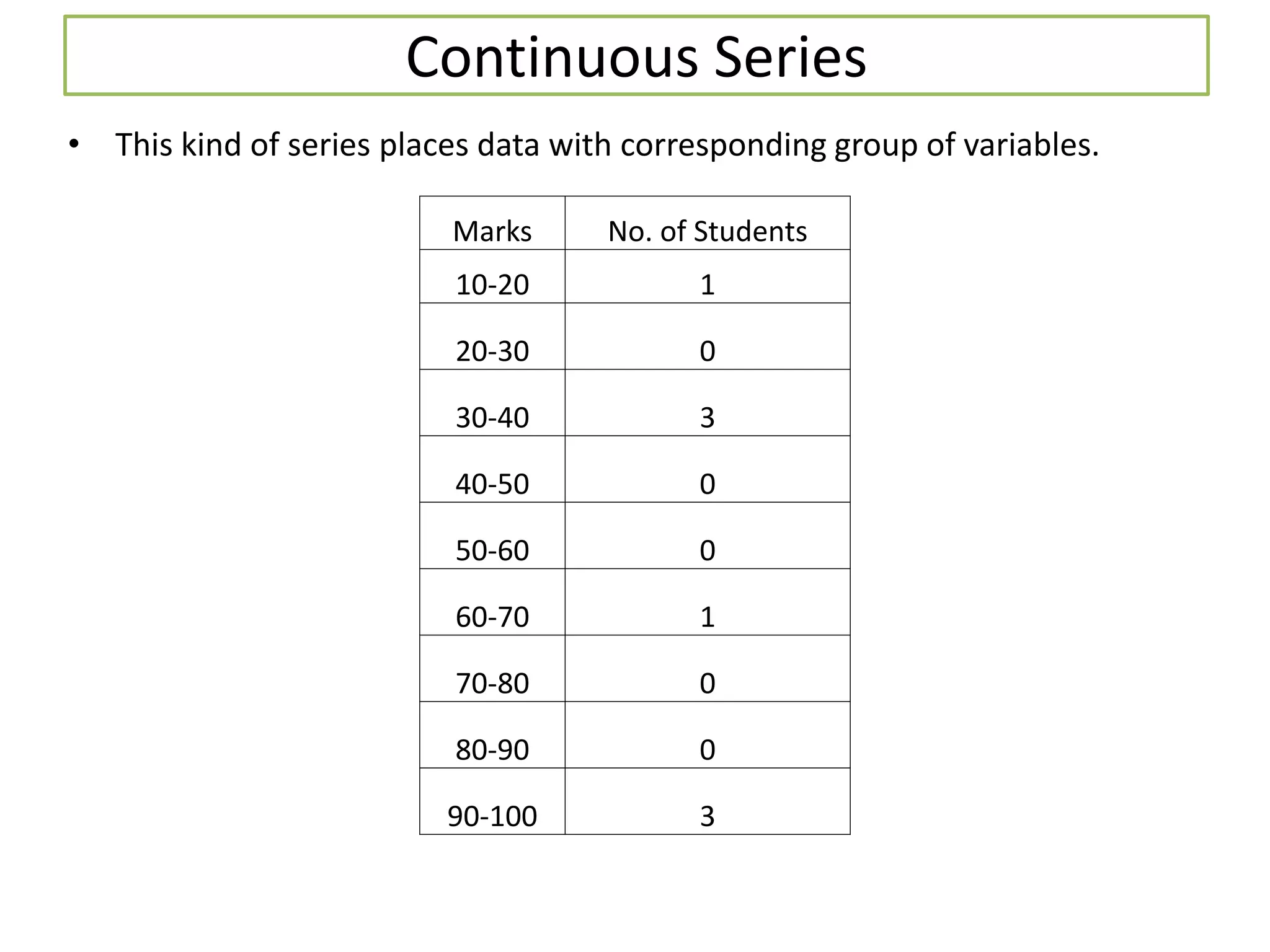
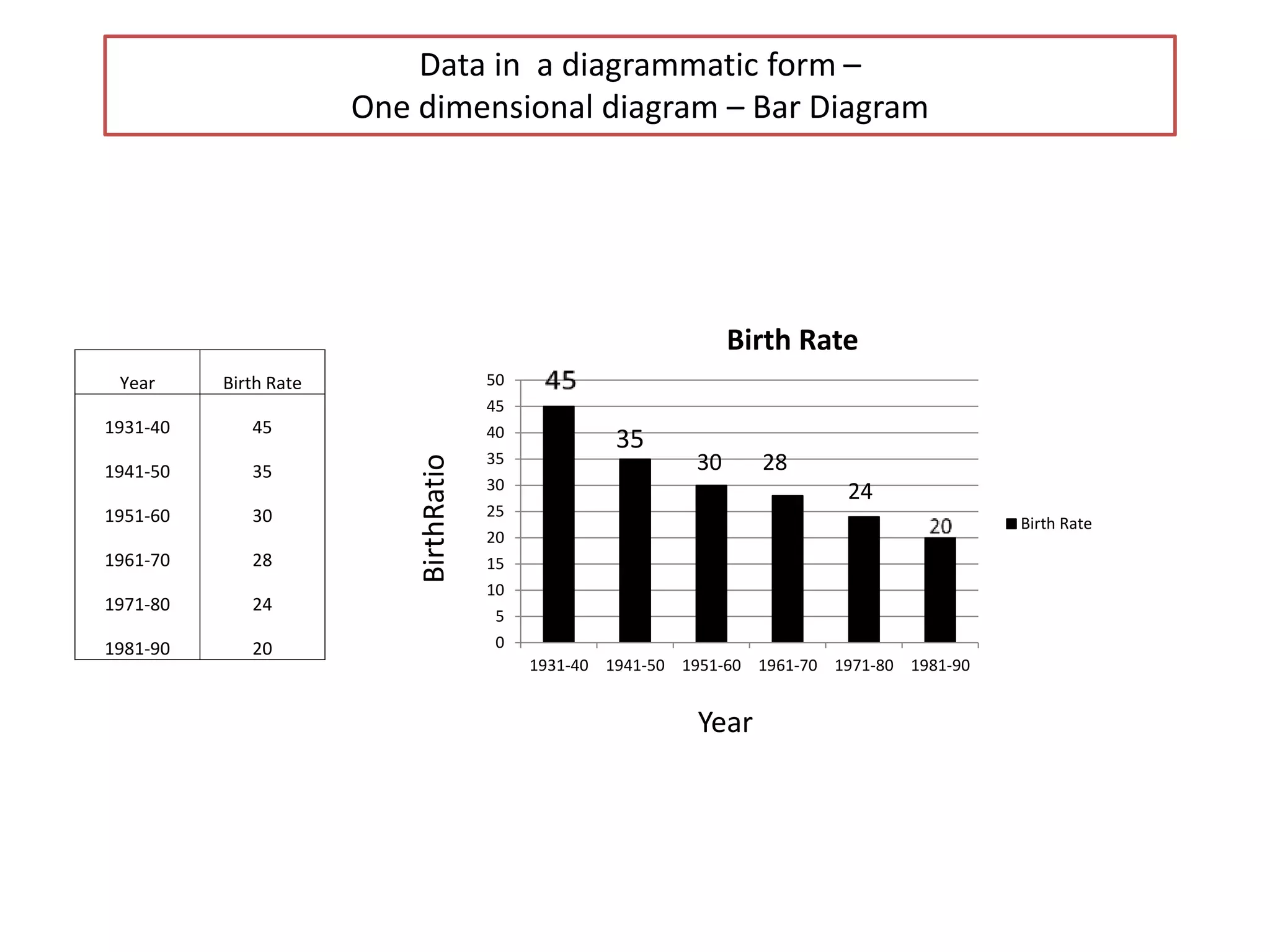
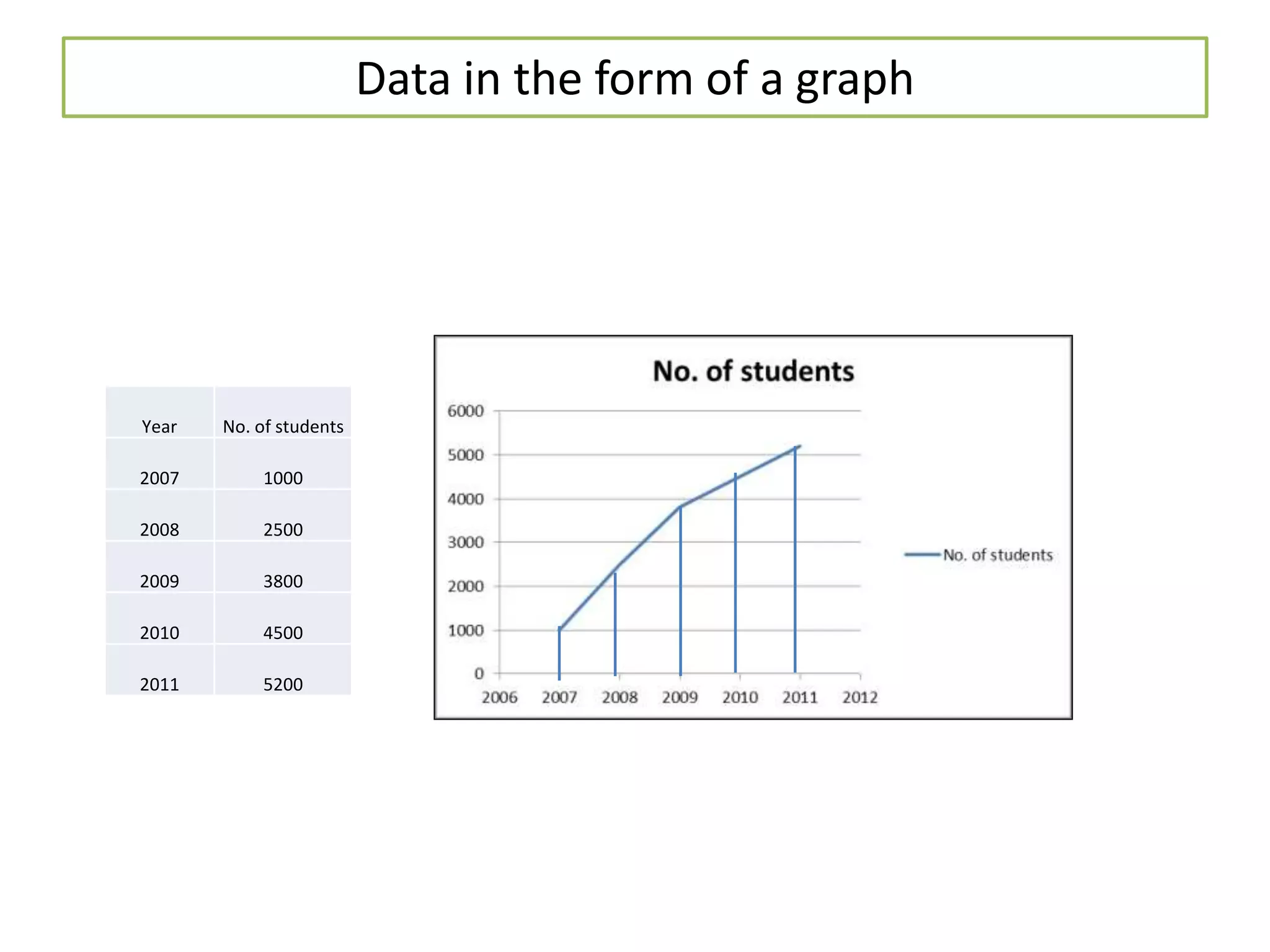
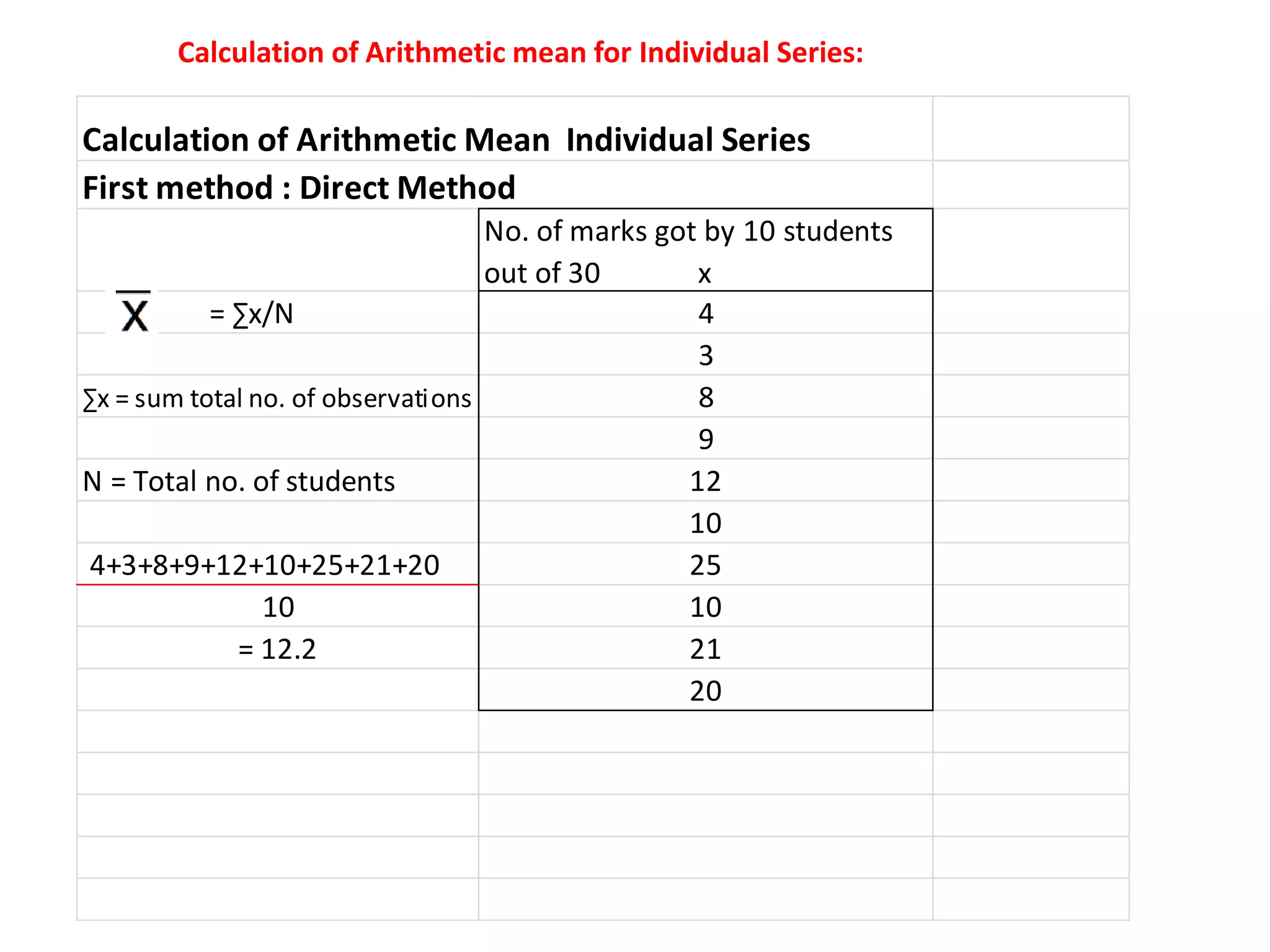
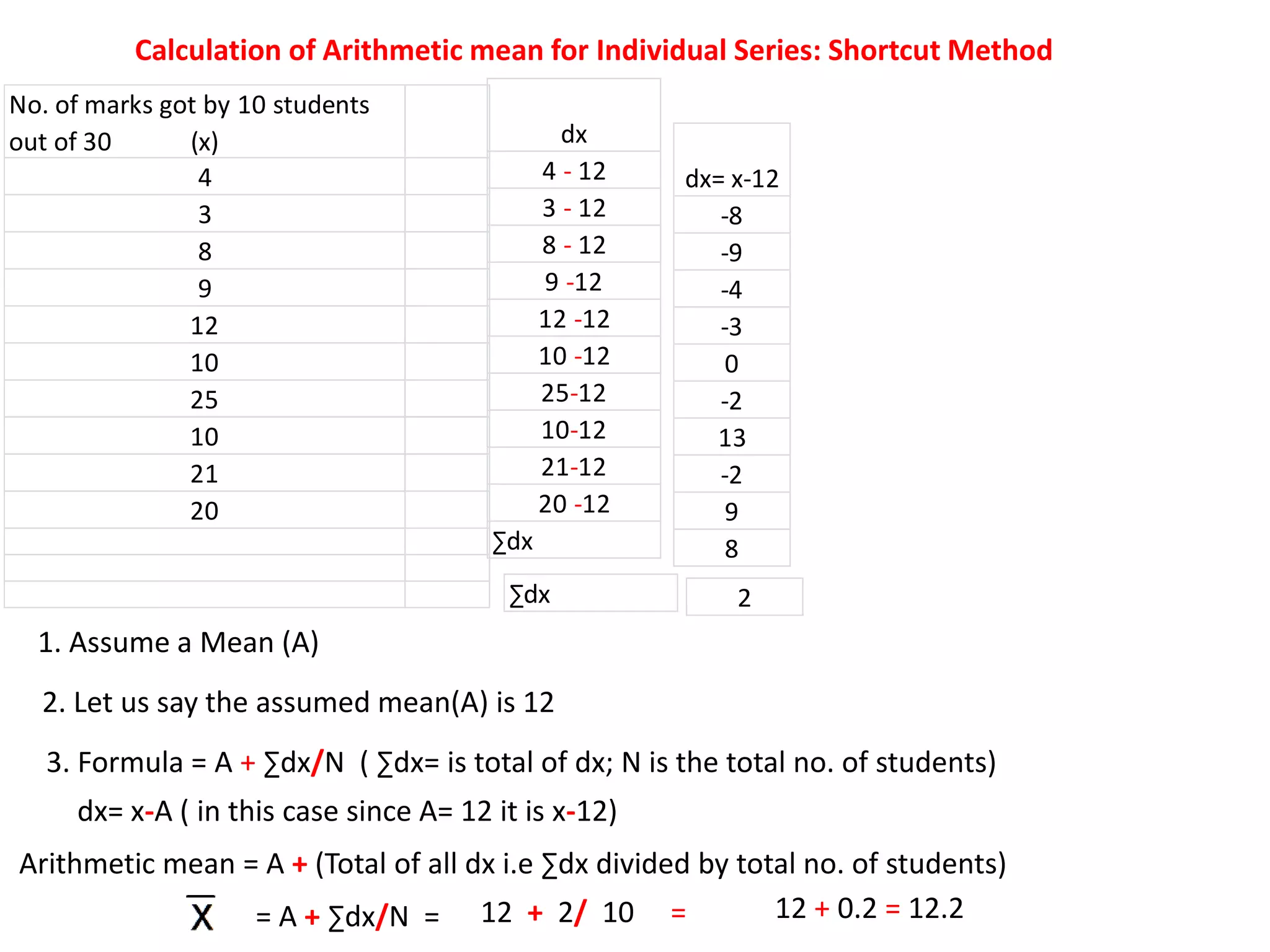
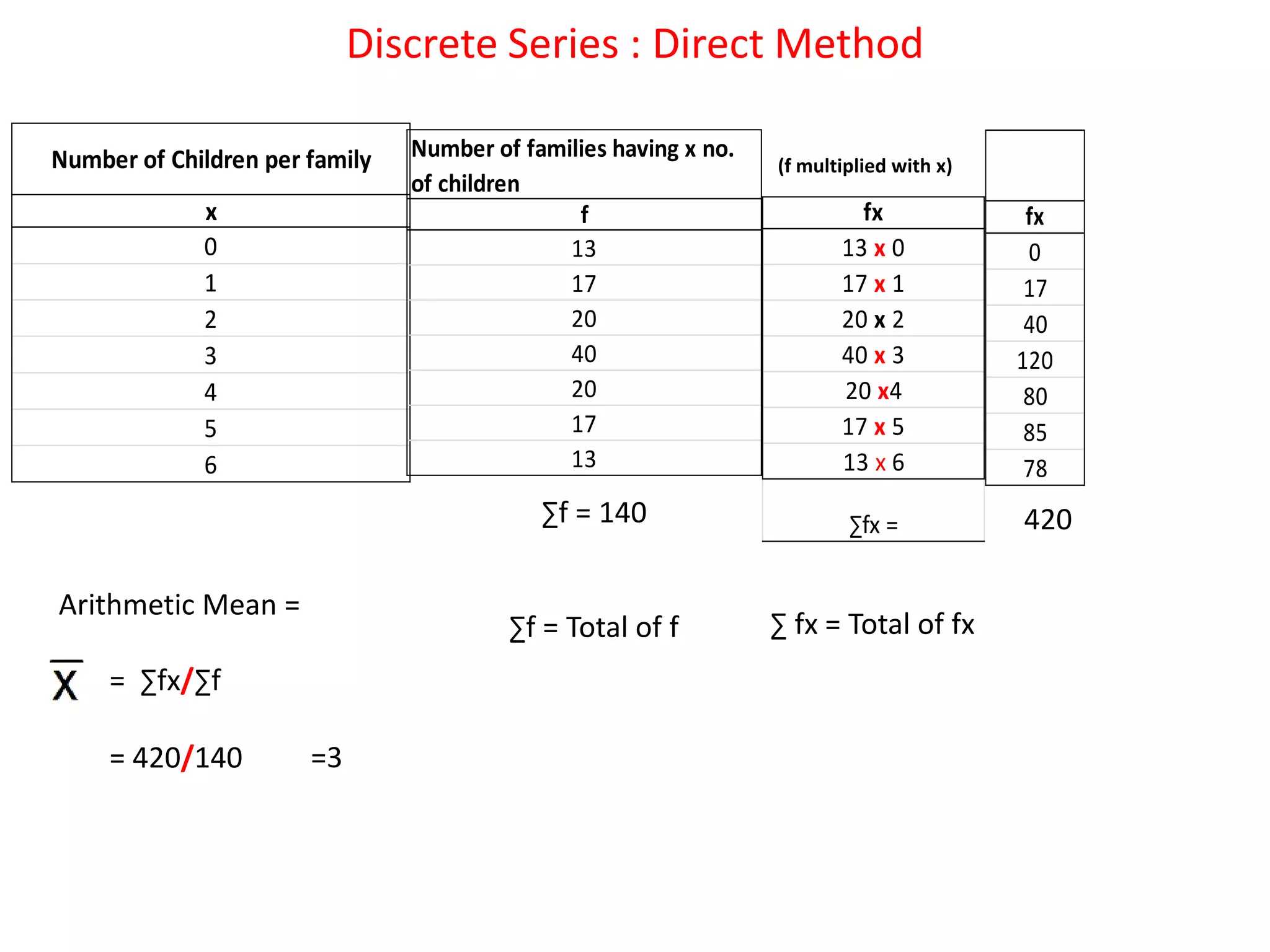
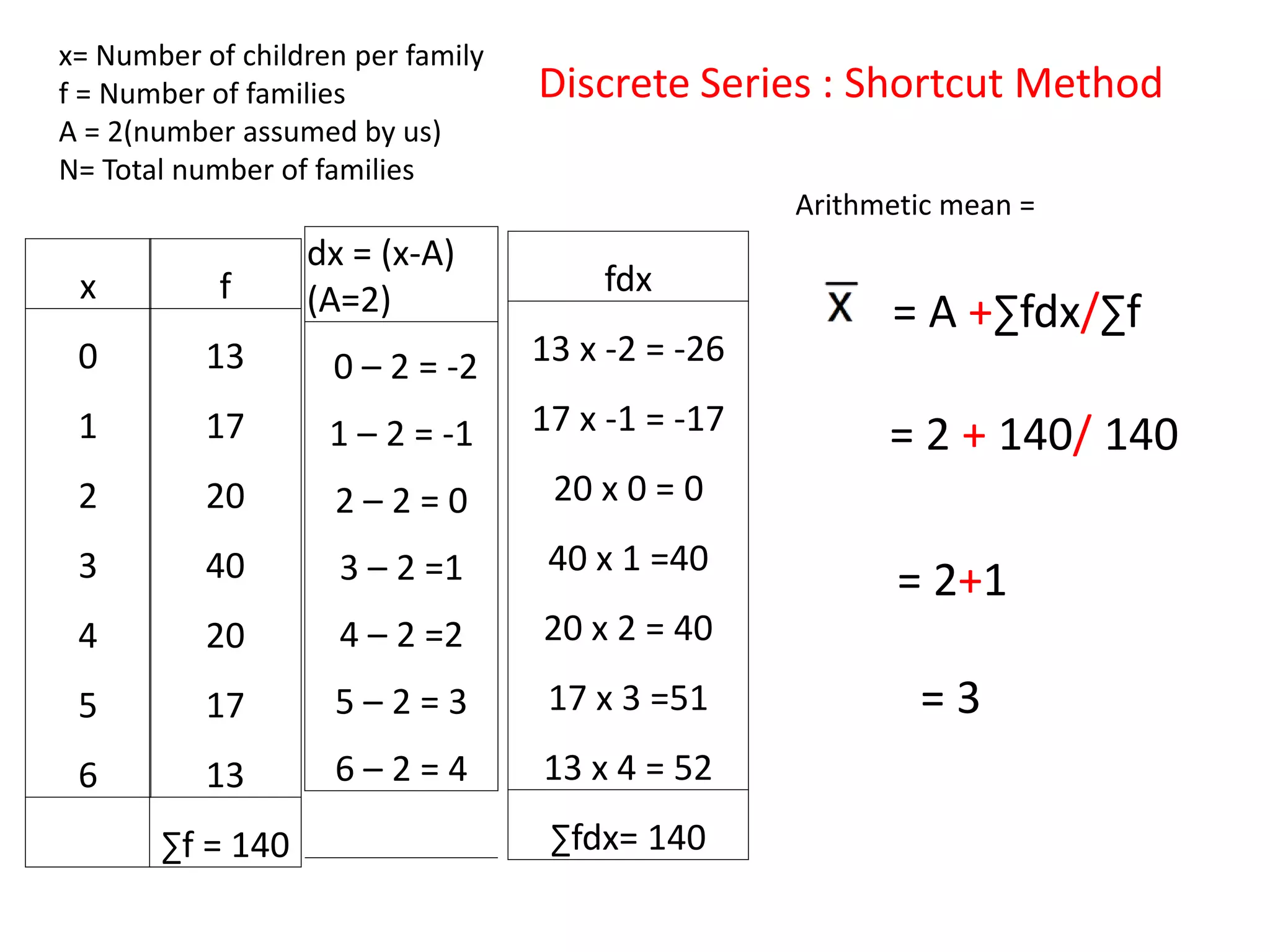
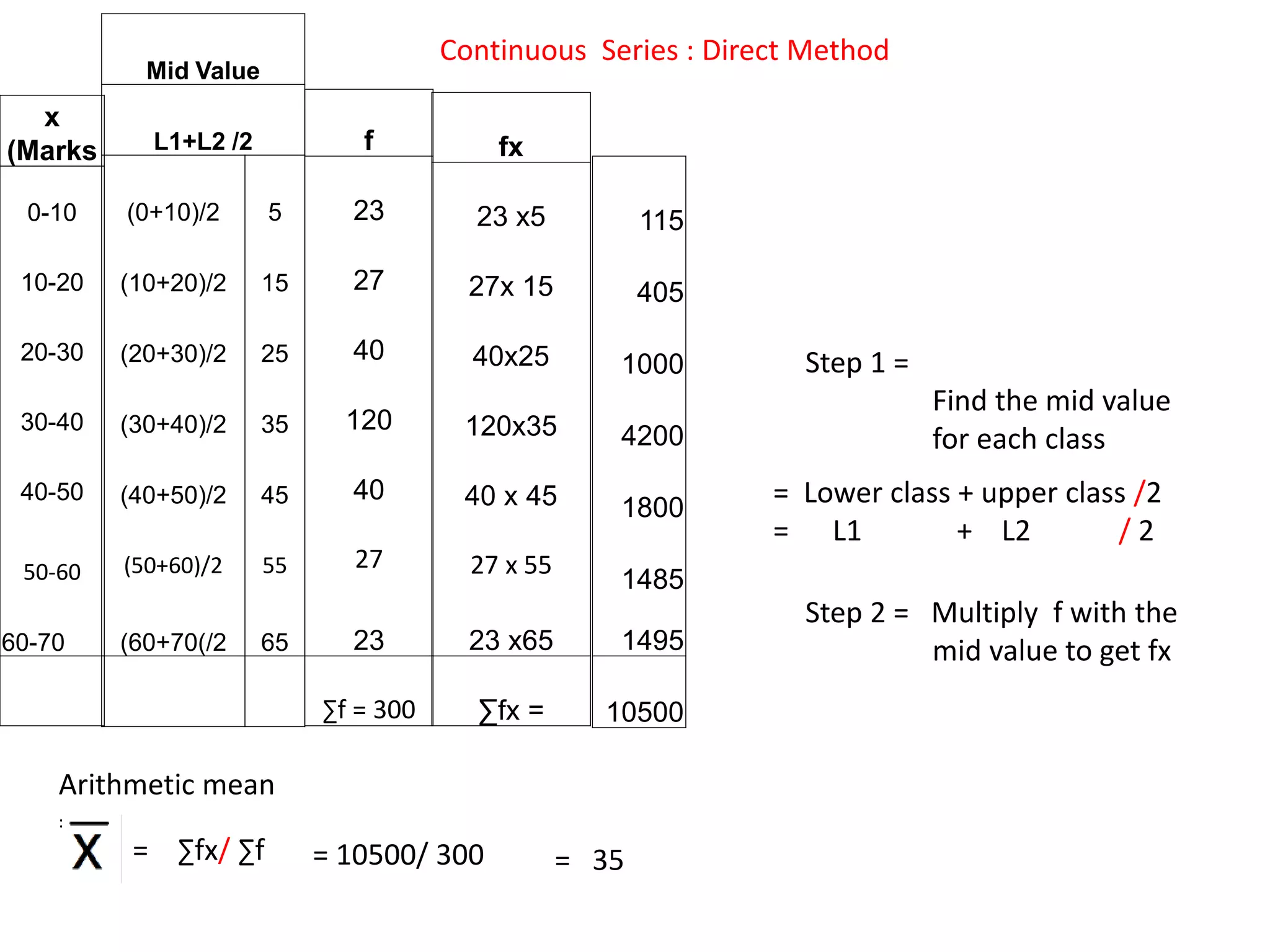
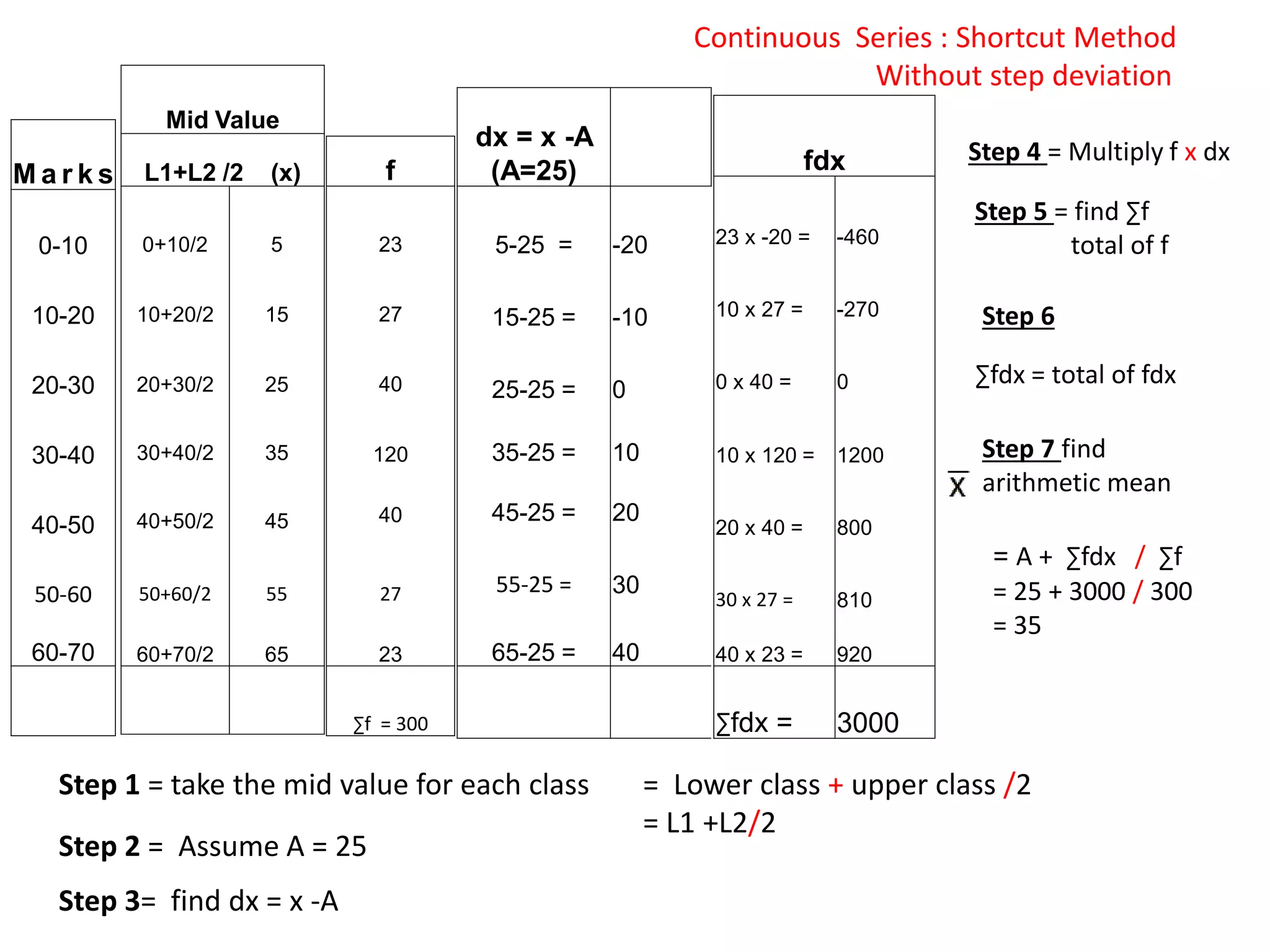
The document discusses various methods for collecting, organizing, and analyzing quantitative data. It describes data as facts expressed numerically that are useful for decision making. Common data types include individual series, discrete series, and continuous series. Methods for calculating the arithmetic mean or average as a measure of central tendency are provided for each data type, including direct formulas and shortcut methods. The goal of statistical analysis is to summarize collected data and identify trends or conclusions.

1. Collection and Presentation of
data

2. Information
• Major source of knowledge
• Helps in making decisions
• With development of Science and technology
the sources of information has increased.
• Books, magazines, internet, mobile phones,
T.V, newspapers are all medium of providing
information.

3. Meaning of Data
• Information is both qualitative and
quantitative.
• In the study of economics quantitative
information's are mostly used for analysis.
• Data means quantitative information which is
expressed as a total.
• Data is useful for making decisions.
• It is also called statistical data.

4. Features/ Characteristics of Data
1. Statistics are aggregate of facts.
– A single fact cannot be considered as a data.
– For e.g. : Suresh got 56 marks in economics.
– This is only a fact not a data.
– The table below gives details of 12 students in a class.
– With the help of this we can compare the performance of the whole class.
– This is an example of DATA.
Students Marks Students Marks
Aditya 95 Harish 35
Bala 90 Kavita 30
Chetna 75 Leena 85
Dinesh 65 Manoj 20
Farida 90 Ravi 90
Gowri 100 Satish 80

5. 3. Data are affected by multiple causes.
• Data are affected by many factors.
• Example: rise in price can be due to rise in demand or fall in supply
or rise in taxes.
2. They are expressed as numbers.
(a) When facts are given by counting or calculation, then it is called data.
(b) Hence data is quantitative and not qualitative.
Features/ Characteristics of Data

6. 4. Statistics does not give 100% accuracy.
– If a doctor invents a medicine to control diabetes and after conducting
a research he states that 90% of the people responded well to the
medicine.
– This medicine is then considered good.
5. Data is always collected for a predetermined purpose.
Features/ Characteristics of Data

7. Statistics important in Economics
• In economics statistics is important –
• 1) In economic planning.
– The data of the previous years are used to prepare plans
for the future.
– Forecasting is done on the basis of economic planning.
• 2) In calculating national income.
– In order to know the state of the economy it is important
to know the national income.

8. • 3) In making government policies.
• Statistical data are widely used by governments to frame
policies for economic development of the country.
• On the basis of Data collected the government had to make
policy to remove poverty and unemployment.
• The government introduced the National Employment
Guarantee Scheme, by which the government guarantees an
unemployed person at least 100 days of employment in a year.

9. Primary data and Secondary data.
• On the basis of source of collection data can
be classified as :
• Primary Data:
– Data which is collected for the first time for a
particular purpose is called Primary data.
• Secondary Data:
– When we use data that has already been collected
by others then it is called Secondary data.

10. Various methods of collecting primary data
• There are five methods of collecting primary
data. They are –
• 1) Direct personal investigation.
• 2) Indirect investigation.
• 3) Through correspondents.
• 4) By mailed questionnaire.
• 5) Through schedules.

11. Sources of Secondary Data
• Secondary data may exist in the form of published or
unpublished form.
Published form:
– Newspapers and RBI reports.
– Trade association reports.
– Financial data reported in annual reports.
– Reports made and published by UNO, World Bank etc.
– Reports made by SEBI.
 Unpublished form:
• Internal reports of government departments.
• Records maintained by institutions.
• Research reports prepared by students in universities.

12. variable and attribute.
• Variable
• 1)When data can be classified in terms of time or
size, it is called variable.
• 2) For example – height, eight, length, distance
etc.
• Attribute
• 1)Data which cannot be classified in terms of
time or size is called attribute.
• 2)For example – beauty, bravery, intelligence etc.

13. Classification
• The process of arranging raw data into classes
or groups to make it usable is called
classification.
• Data can be classified in the following ways –
• (i) Individual series
• (ii) Discrete series
• (iii) Continuous series

14. Individual series
• In this series items are shown individually with
their corresponding value.
Raw Data -
Data is collected in its
original form.
Array -
This data is then arranged in
ascending or descending
order.
Students Marks Students Marks
Gowri 100 Satish 80
Aditya 95 Chetna 80
Bala 35 Dinesh 65
Farida 90 Harish 35
Ravi 90 Kavita 35
Leena 85 Manoj 20
Students Marks Students Marks
Gowri 100 Chetna 80
Aditya 95 Dinesh 65
Farida 90 Bala 35
Ravi 90 Harish 35
Leena 85 Kavita 35
Satish 80 Manoj 20

15. Discrete Series
• This series shows variables with definite
breaks with their frequencies.
Marks No. of Students
100 1
95 1
90 2
85 1
80 2
65 1
35 3
20 1

16. Continuous Series
• This kind of series places data with corresponding group of variables.
Marks No. of Students
10-20 1
20-30 0
30-40 3
40-50 0
50-60 0
60-70 1
70-80 0
80-90 0
90-100 3

17. Tabulation
• Once data is collected and classified, it can be
put into rows and columns. This process is
called tabulation.

18. Diagrammatic presentation
• The geometrical version of data is diagrammatic
presentation.
• Example – bar diagram is a one dimensional
diagram.

19. Data in a diagrammatic form –
One dimensional diagram – Bar Diagram
Year Birth Rate
1931-40 45
1941-50 35
1951-60 30
1961-70 28
1971-80 24
1981-90 20 0
5
10
15
20
25
30
35
40
45
50
1931-40 1941-50 1951-60 1961-70 1971-80 1981-90
Birth Rate
Birth Rate
Year
BirthRatio
24 24
2830
35

20. Data in the form of a graph
Year No. of students
2007 1000
2008 2500
2009 3800
2010 4500
2011 5200

21. Analysis of Data

22. • Analysis of Data
• After Data has been collected, classified,
tabulated and presented, it is studied to reach
a conclusion.
• This is called analysis of data.

23. Central tendency
• One of the main aims of statistical analysis is
to get one single value that describes the
whole data.
• This single value is called average or mean.
• An average measures the tendency of data to
move in a particular direction.
• The tendency of data to group around the
central value or valve is called central
tendency.

24. Arithmetic Mean
• Arithmetic mean is one of the methods of calculating central tendency.
• It is an average.
• It is calculated to
reach
a single value
which
represents
the entire data.
• Calculating an Average
• For example (1, 2, 2, 2, 3, 9). The arithmetic mean is
1 + 2 + 2 + 2 + 3 + 9 = 19 = 3.17
6 6
Arithmetic means are used in situations such as
working out cricket averages.
Arithmetic means are used in calculating average incomes.

25. Functions and purpose of average
• To make a summary of the collected information.
• To make comparisons between two or more groups
• To reach a value that represents the entire data.
• To make future policy and programme.

26. Calculation of Arithmetic Mean Individual Series
First method : Direct Method
No. of marks got by 10 students
out of 30 x
= ∑x/N 4
3
∑x = sum total no. of observations 8
9
N = Total no. of students 12
10
4+3+8+9+12+10+25+21+20 25
10 10
= 12.2 21
20
Calculation of Arithmetic mean for Individual Series:

27. No. of marks got by 10 students
out of 30 (x)
4
3
8
9
12
10
25
10
21
20
1. Assume a Mean (A)
2. Let us say the assumed mean(A) is 12
3. Formula = A + ∑dx/N ( ∑dx= is total of dx; N is the total no. of students)
dx= x-A ( in this case since A= 12 it is x-12)
Arithmetic mean = A + (Total of all dx i.e ∑dx divided by total no. of students)
12 + 2/ 10 = 12 + 0.2 = 12.2
dx
4 - 12
3 - 12
8 - 12
9 -12
12 -12
10 -12
25-12
10-12
21-12
20 -12
∑dx
dx= x-12
-8
-9
-4
-3
0
-2
13
-2
9
8
∑dx 2
= A + ∑dx/N =
Calculation of Arithmetic mean for Individual Series: Shortcut Method

28. Discrete Series : Direct Method
Number of Children per family
x
0
1
2
3
4
5
6
Number of families having x no.
of children
f
13
17
20
40
20
17
13
fx
13 x 0
17 x 1
20 x 2
40 x 3
20 x4
17 x 5
13 x 6
∑fx =
fx
0
17
40
120
80
85
78
∑f = 140 420
∑f = Total of f ∑ fx = Total of fx
Arithmetic Mean =
= ∑fx/∑f
= 420/140 =3
(f multiplied with x)

29. Discrete Series : Shortcut Method
x= Number of children per family
f = Number of families
A = 2(number assumed by us)
N= Total number of families
x
0
1
2
3
4
5
6
f
13
17
20
40
20
17
13
∑f = 140
dx = (x-A)
(A=2)
0 – 2 = -2
1 – 2 = -1
2 – 2 = 0
3 – 2 =1
4 – 2 =2
5 – 2 = 3
6 – 2 = 4
fdx
13 x -2 = -26
17 x -1 = -17
20 x 0 = 0
40 x 1 =40
20 x 2 = 40
17 x 3 =51
13 x 4 = 52
∑fdx= 140
= A +∑fdx/∑f
= 2 + 140/ 140
= 2+1
= 3
Arithmetic mean =

30. Continuous Series : Direct Method
x
(Marks
0-10
10-20
20-30
30-40
40-50
50-60
60-70
Mid Value
L1+L2 /2
(0+10)/2 5
(10+20)/2 15
(20+30)/2 25
(30+40)/2 35
(40+50)/2 45
(50+60)/2 55
(60+70(/2 65
f
23
27
40
120
40
27
23
∑f = 300
fx
23 x5
27x 15
40x25
120x35
40 x 45
27 x 55
23 x65
∑fx =
Step 1 =
Find the mid value
for each class
= Lower class + upper class /2
= L1 + L2 / 2
Step 2 = Multiply f with the
mid value to get fx
Arithmetic mean
=
= ∑fx/ ∑f = 35= 10500/ 300
115
405
1000
4200
1800
1485
1495
10500

31. Continuous Series : Shortcut Method
Without step deviation
M a r k s
0-10
10-20
20-30
30-40
40-50
50-60
60-70
Mid Value
L1+L2 /2 (x)
0+10/2 5
10+20/2 15
20+30/2 25
30+40/2 35
40+50/2 45
50+60/2 55
60+70/2 65
f
23
27
40
120
40
27
23
∑f = 300
dx = x -A
(A=25)
5-25 = -20
15-25 = -10
25-25 = 0
35-25 = 10
45-25 = 20
55-25 = 30
65-25 = 40
fdx
23 x -20 = -460
10 x 27 = -270
0 x 40 = 0
10 x 120 = 1200
20 x 40 = 800
30 x 27 = 810
40 x 23 = 920
∑fdx = 3000
Step 1 = take the mid value for each class = Lower class + upper class /2
= L1 +L2/2
Step 2 = Assume A = 25
Step 3= find dx = x -A
Step 4 = Multiply f x dx
Step 5 = find ∑f
total of f
∑fdx = total of fdx
Step 6
Step 7 find
arithmetic mean
= A + ∑fdx / ∑f
= 25 + 3000 / 300
= 35

32. Summary of the Formulae’s for calculating arithmetic mean ;
• Individual Series :
Direct Method : (∑x)
(N )
Shortcut Method = A +
∑𝐝𝐱
𝐍
• Discrete Series :
Direct Method = (∑fx)
(∑f)
Shortcut Method = A + (∑fdx)
(∑f)
Continuous Method :
Direct Method (∑fx)
(∑f)
Shortcut Method A+ (∑fdx)
(∑f)
Shortcut Method (with step deviation)
A+ (∑fdx') x c
(∑f)

33. Thank You