Downloaded 216 times
Uploaded byBhargav Veepuri
8.1. microtech ion implant,1,2
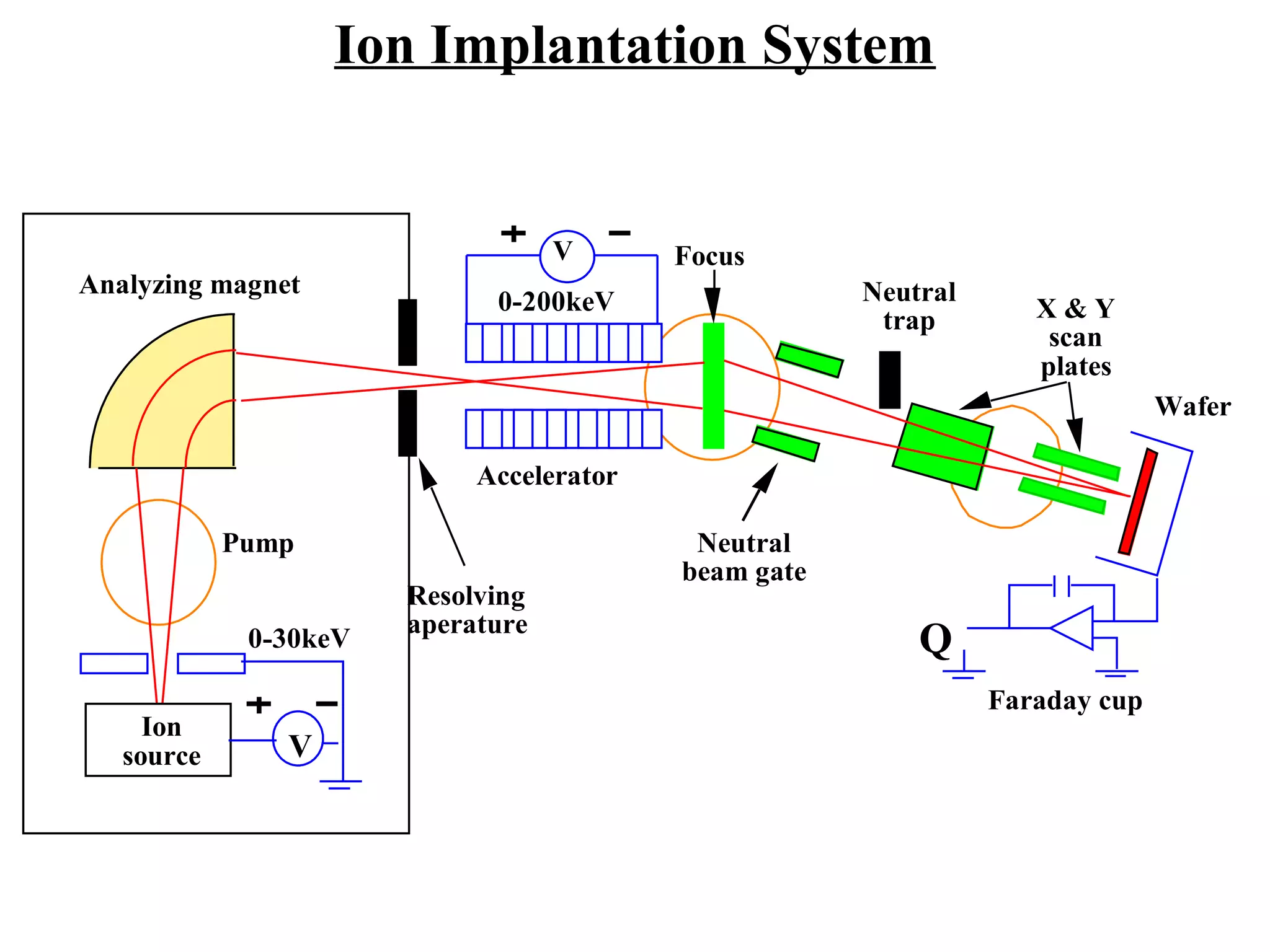
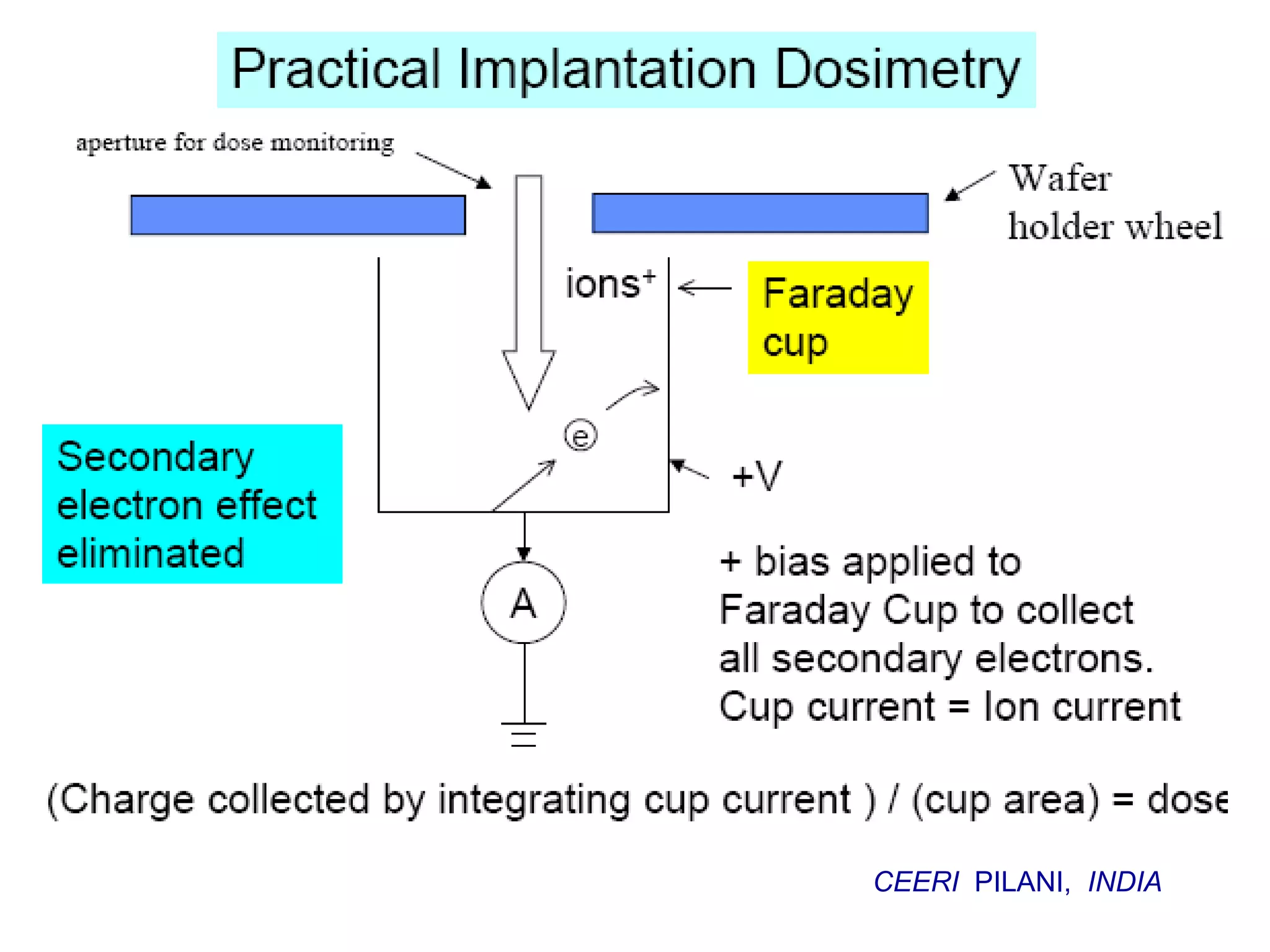
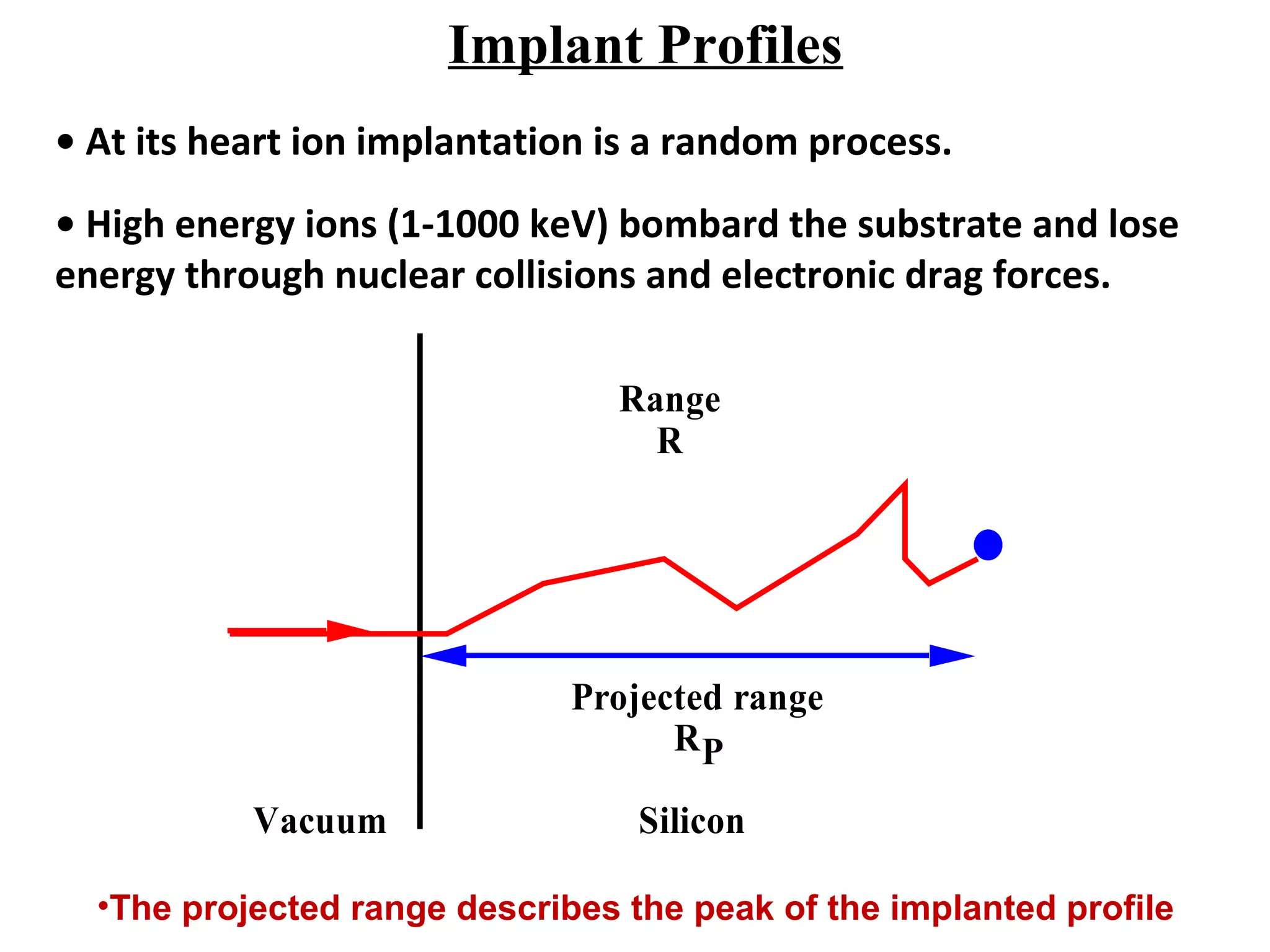
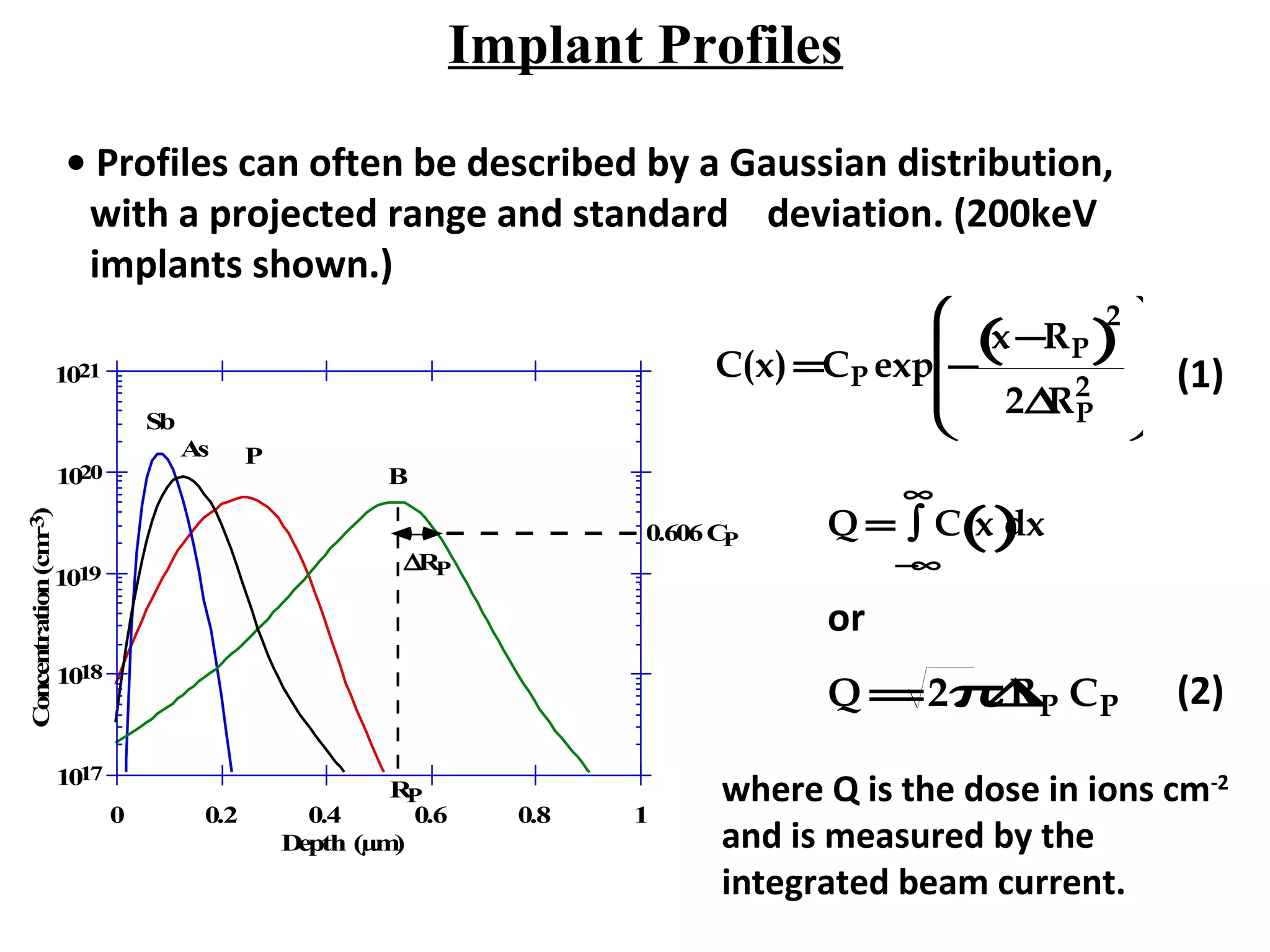
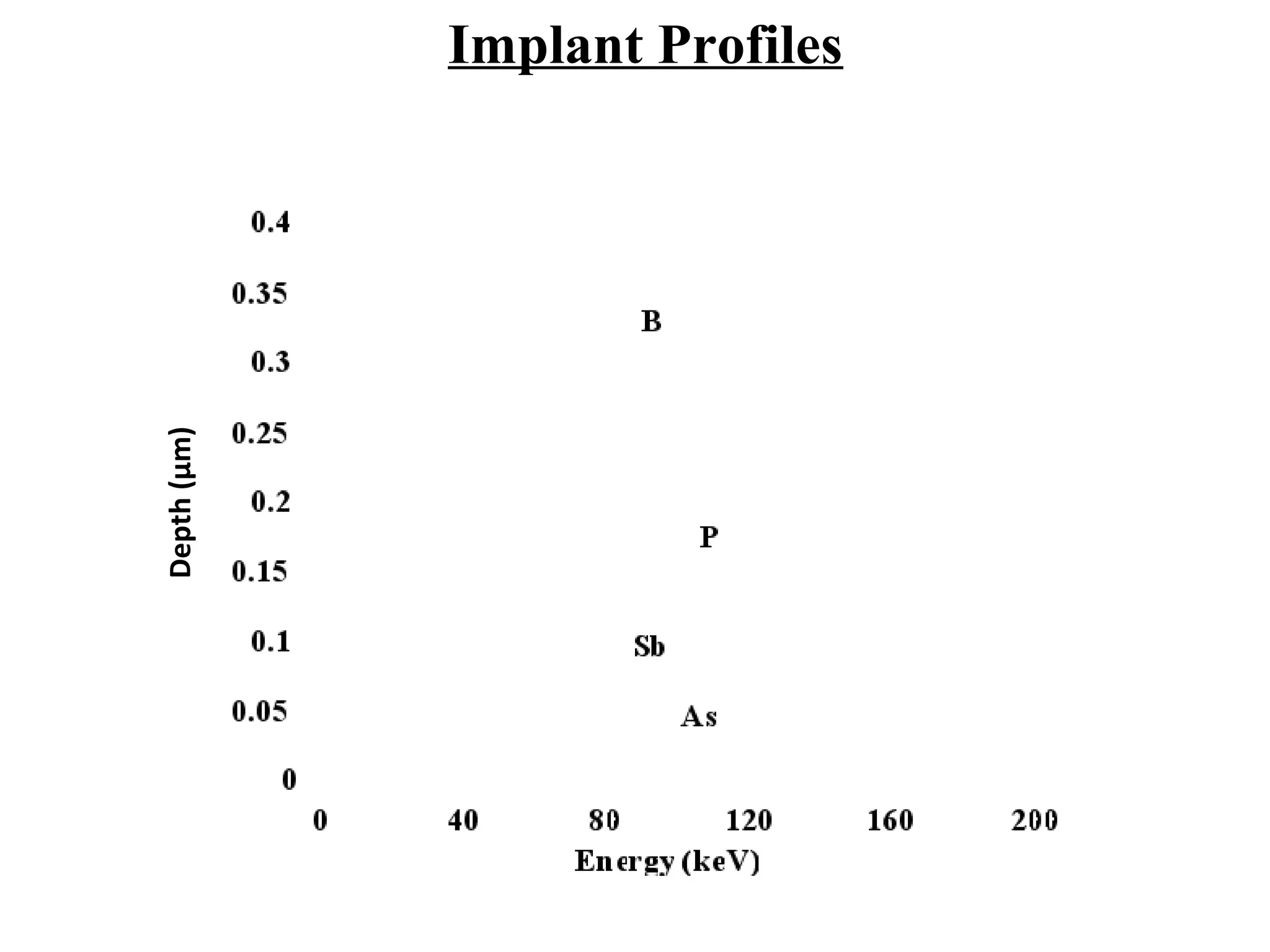
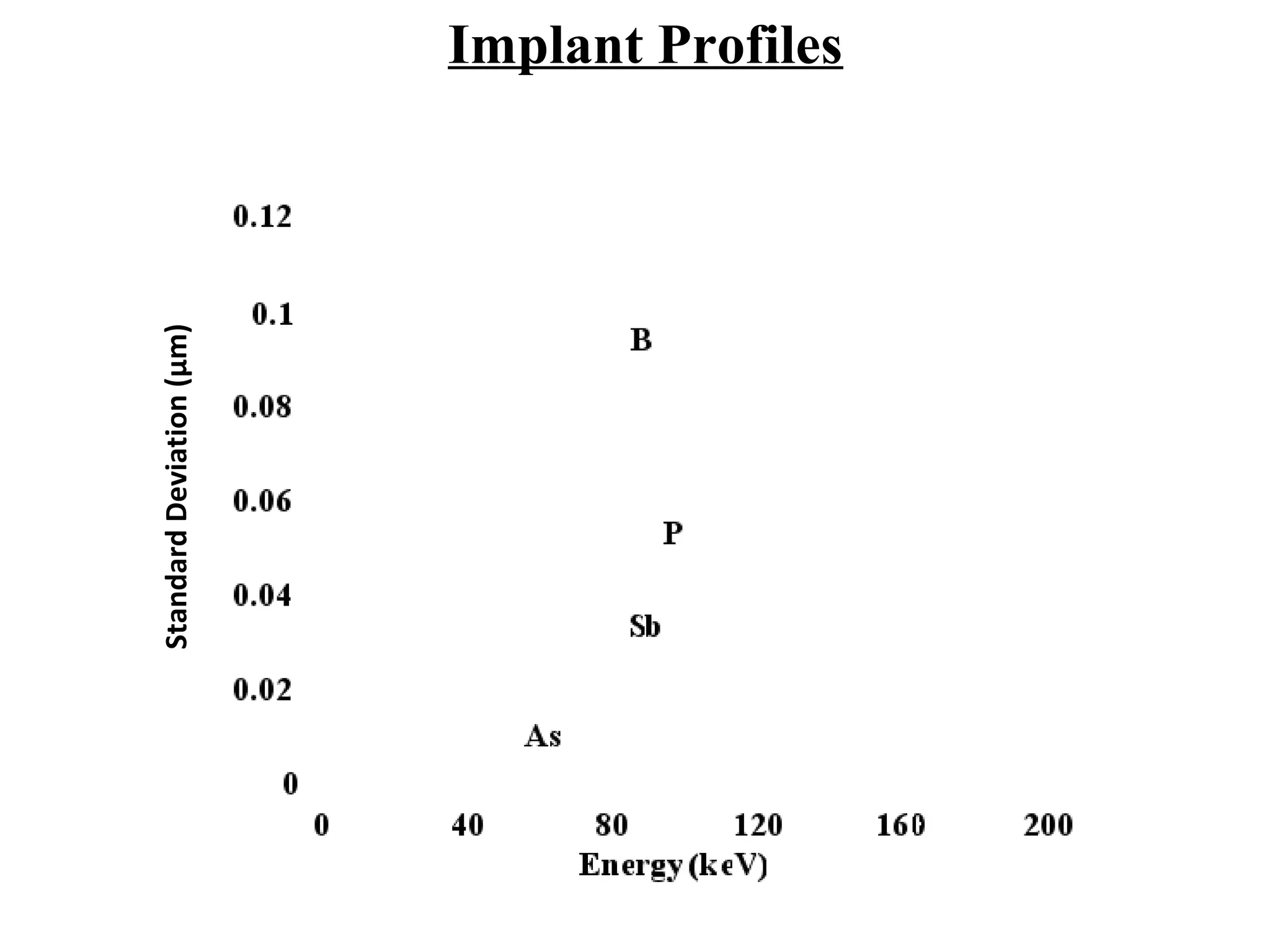
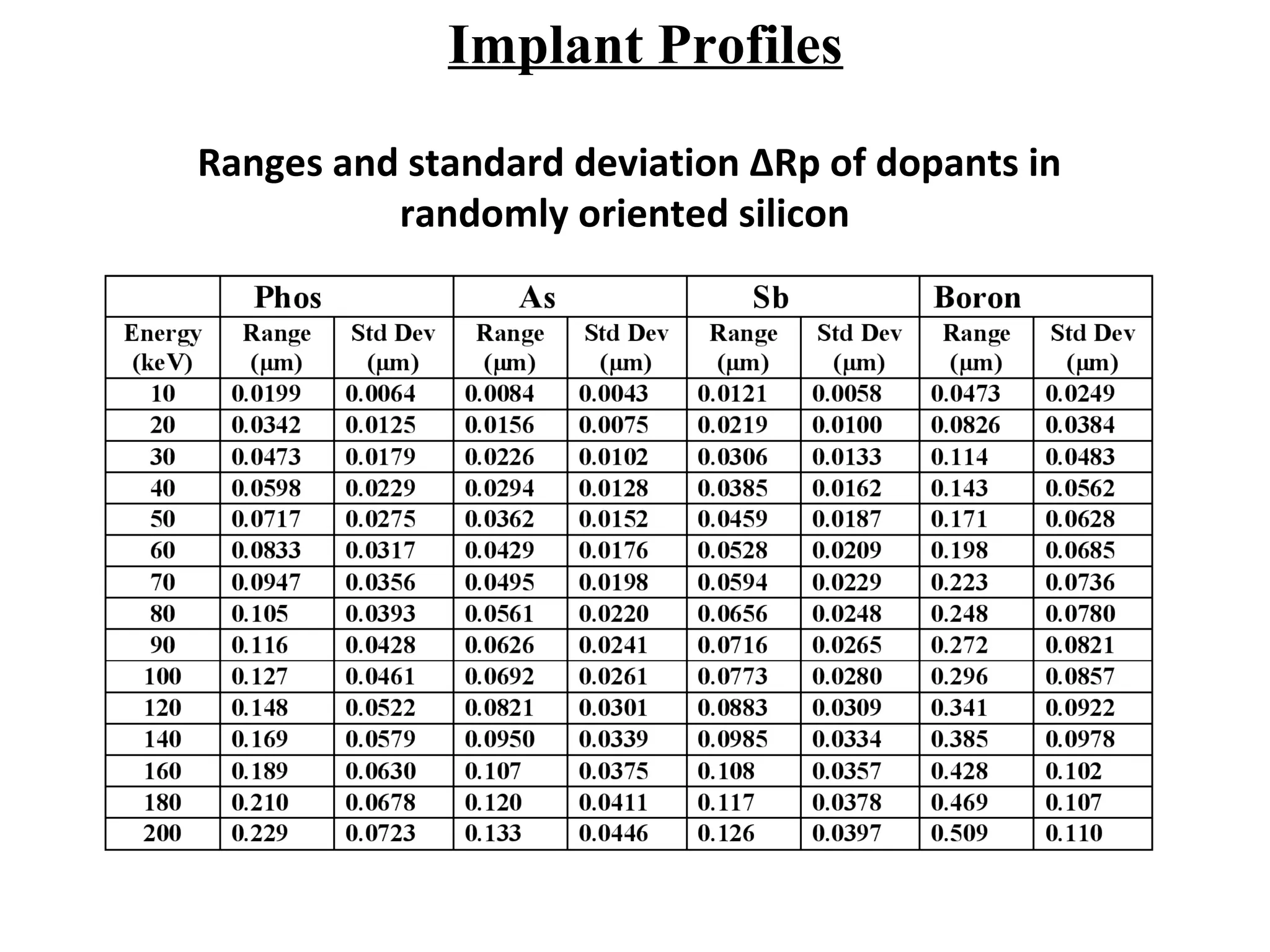
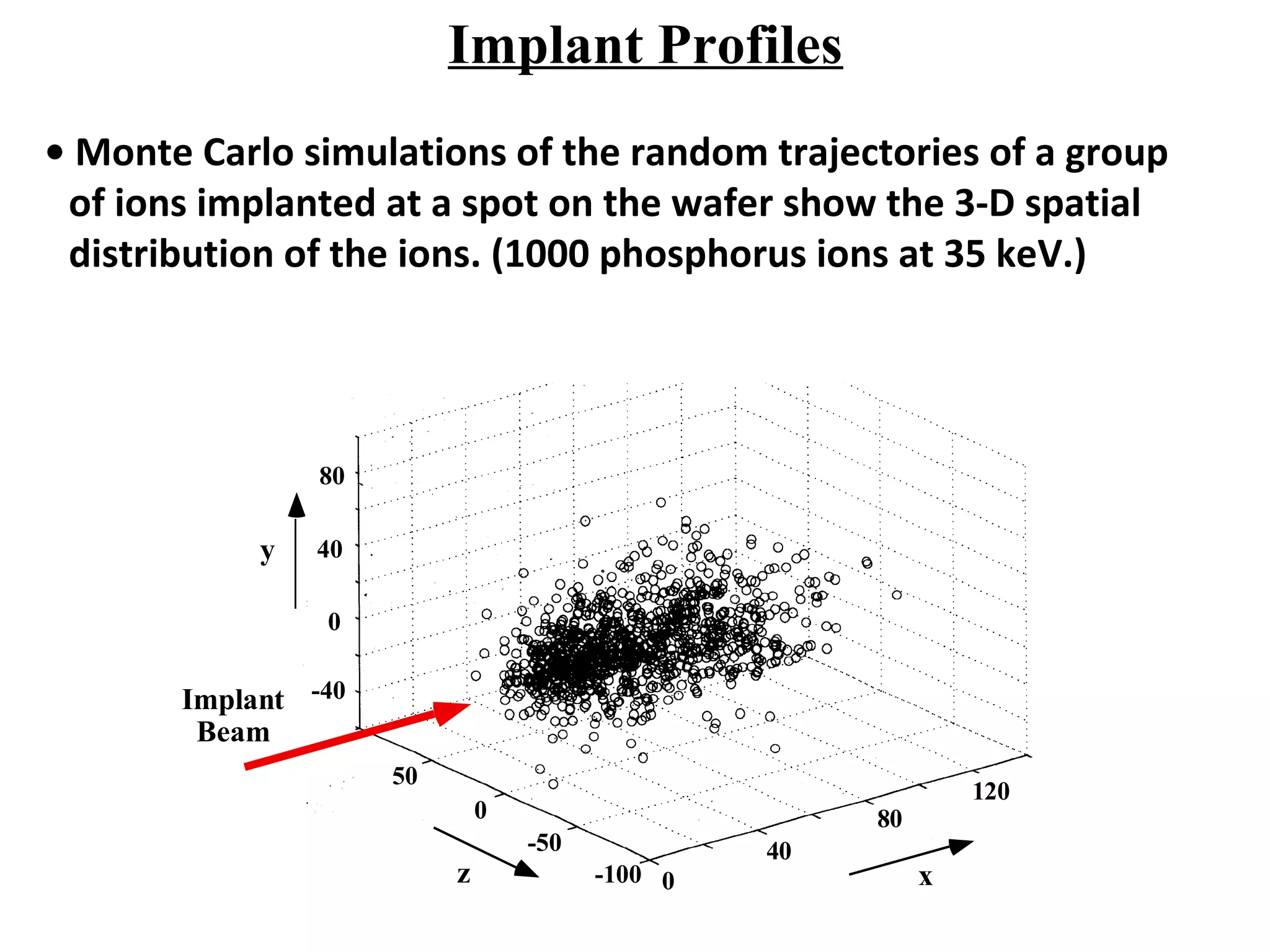
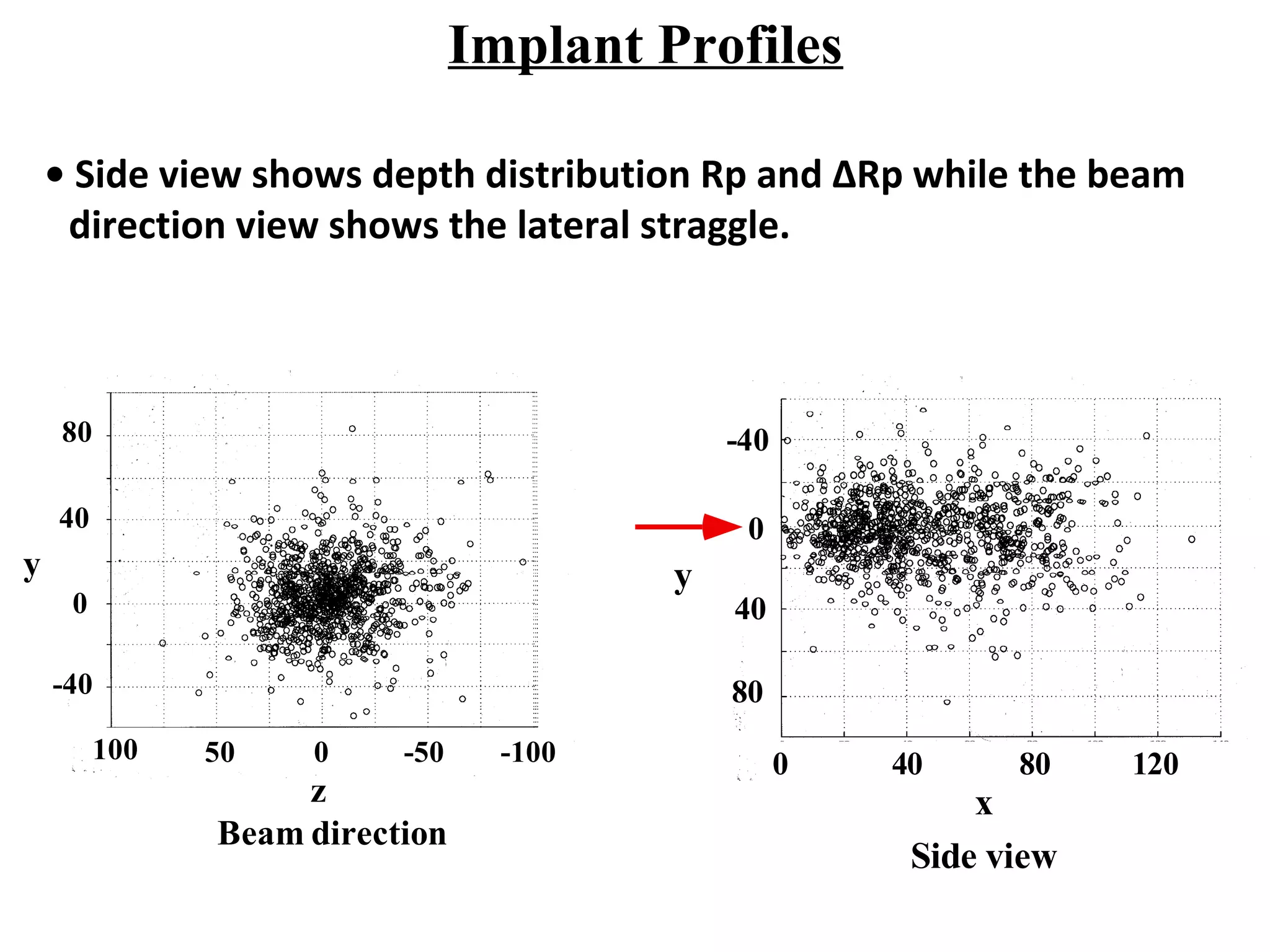
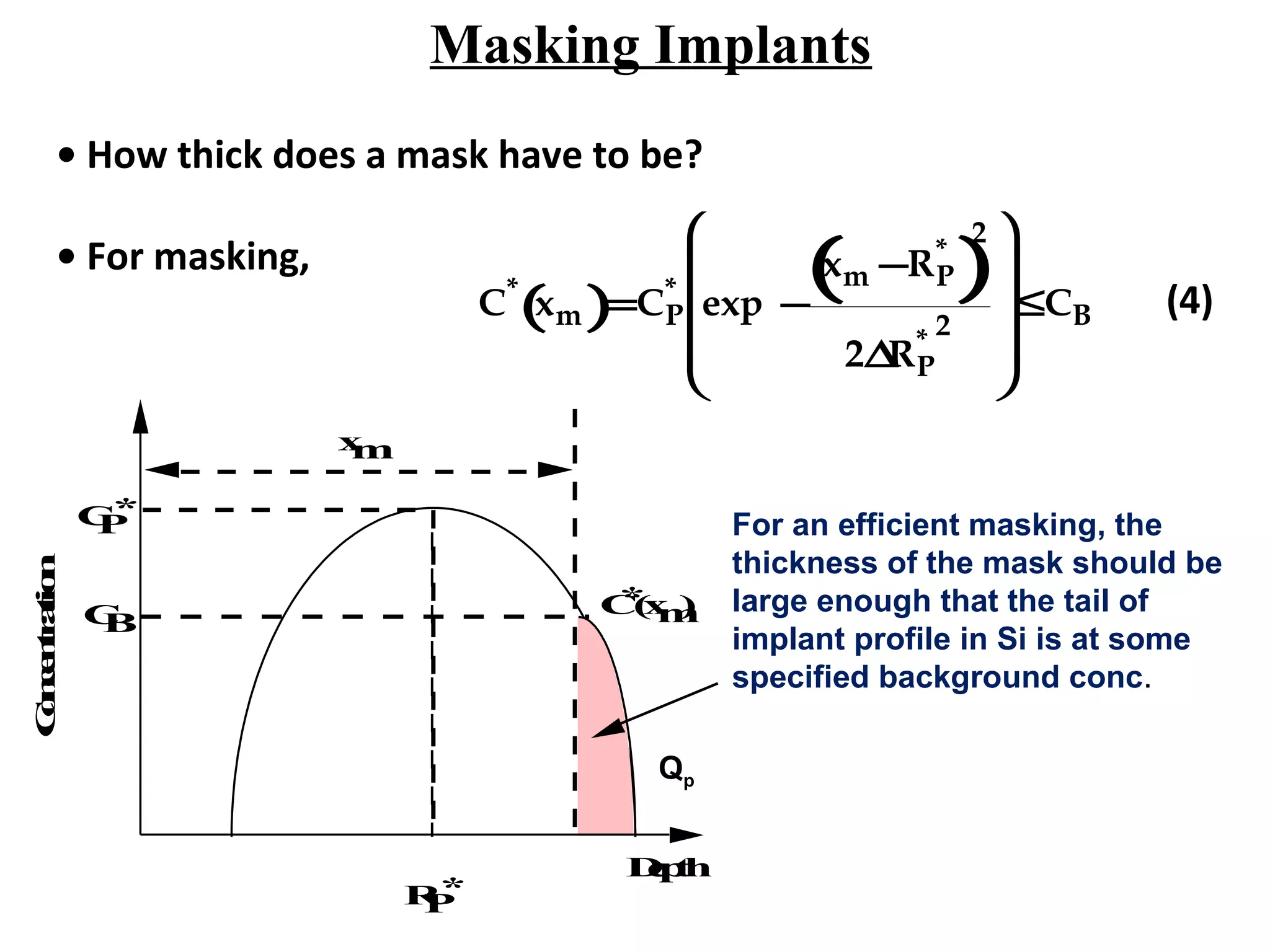
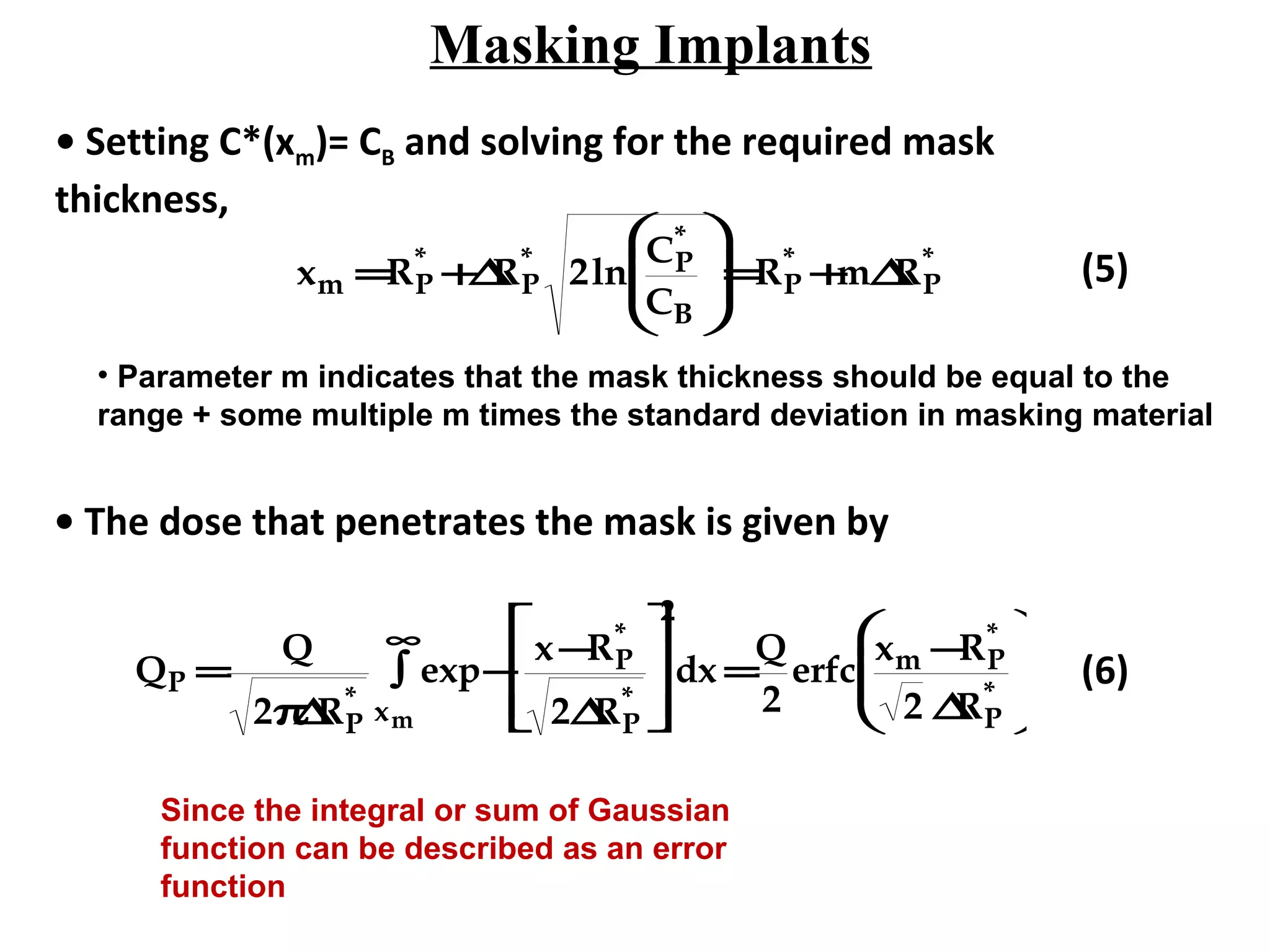
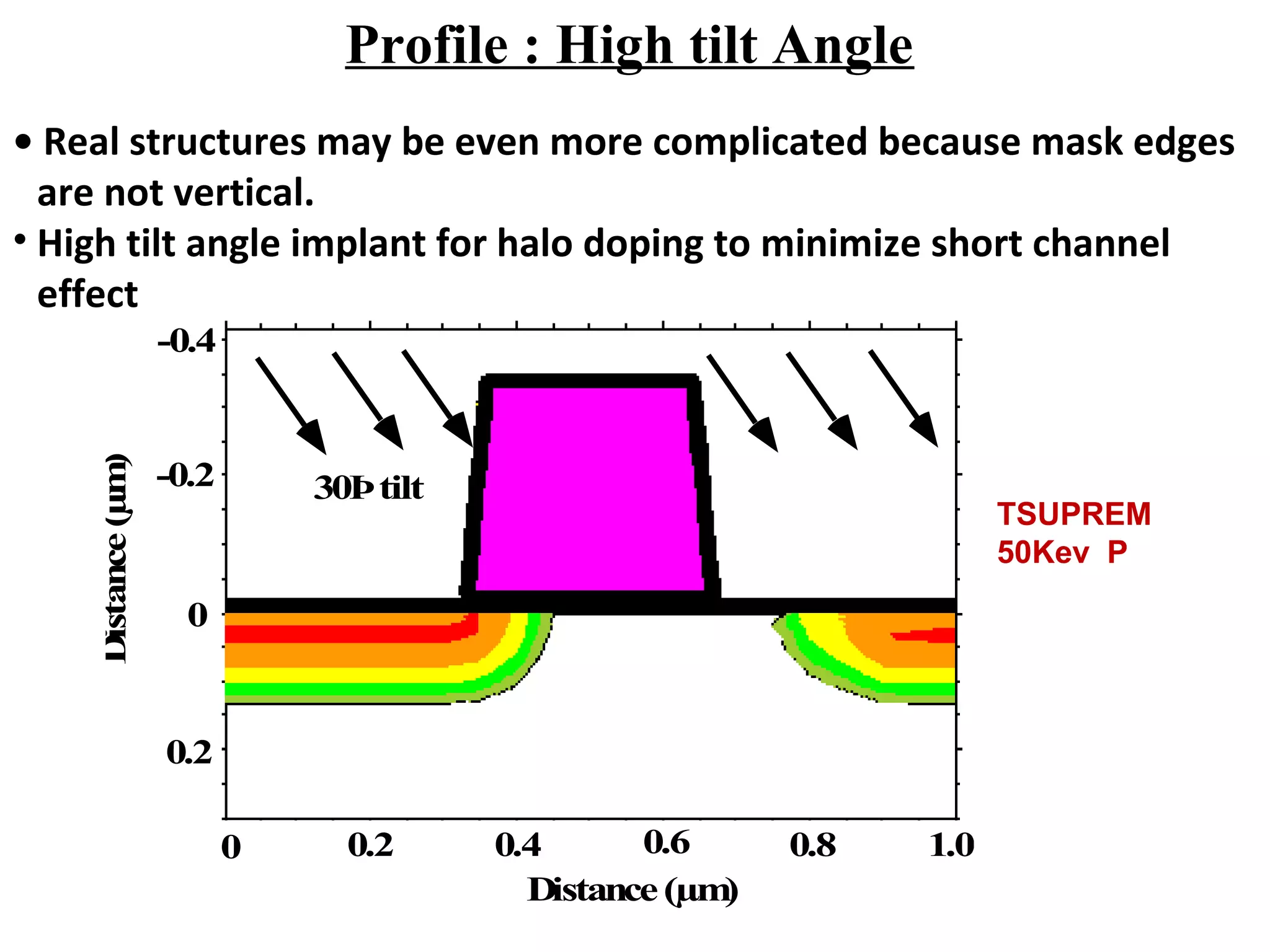
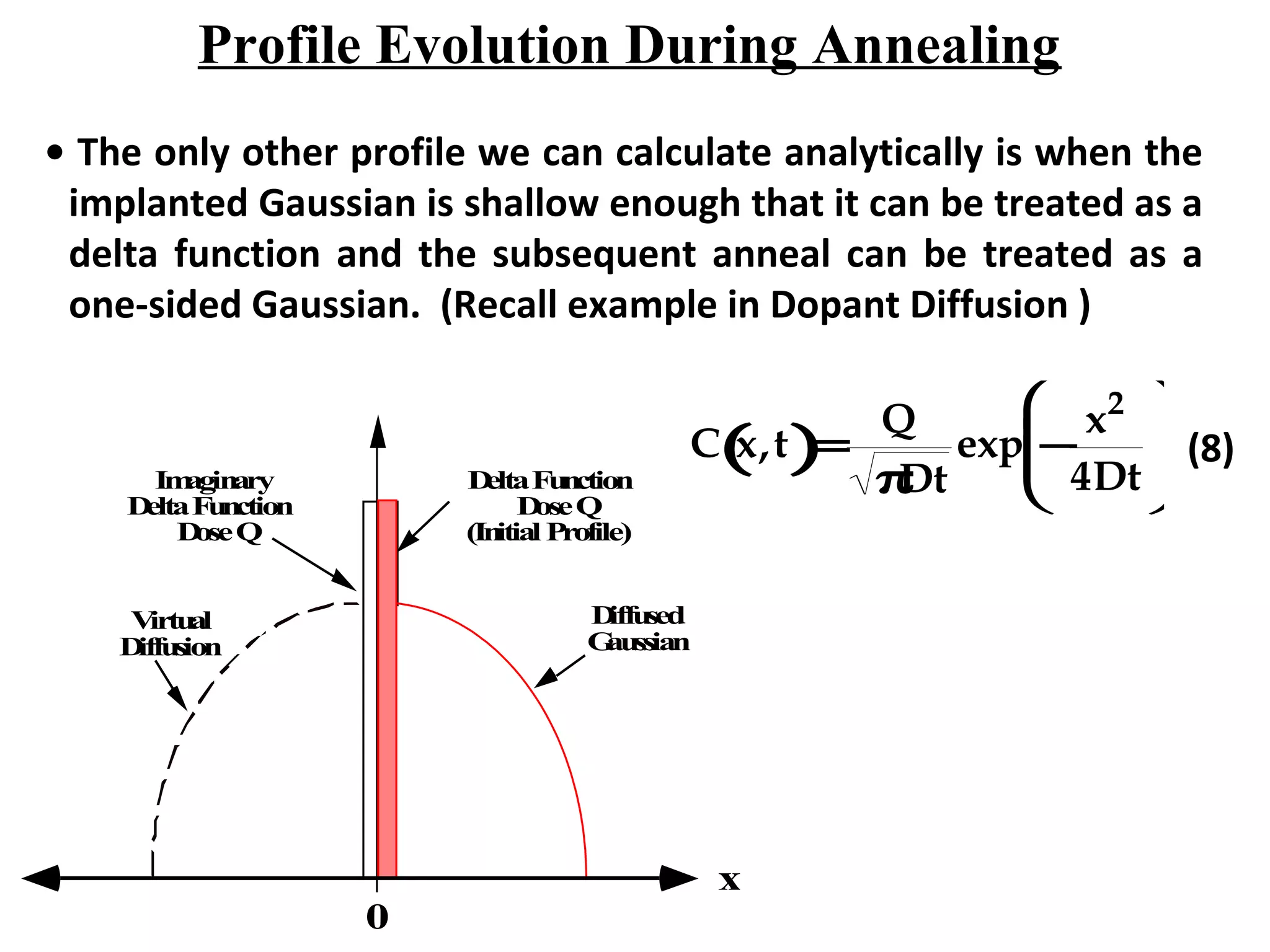
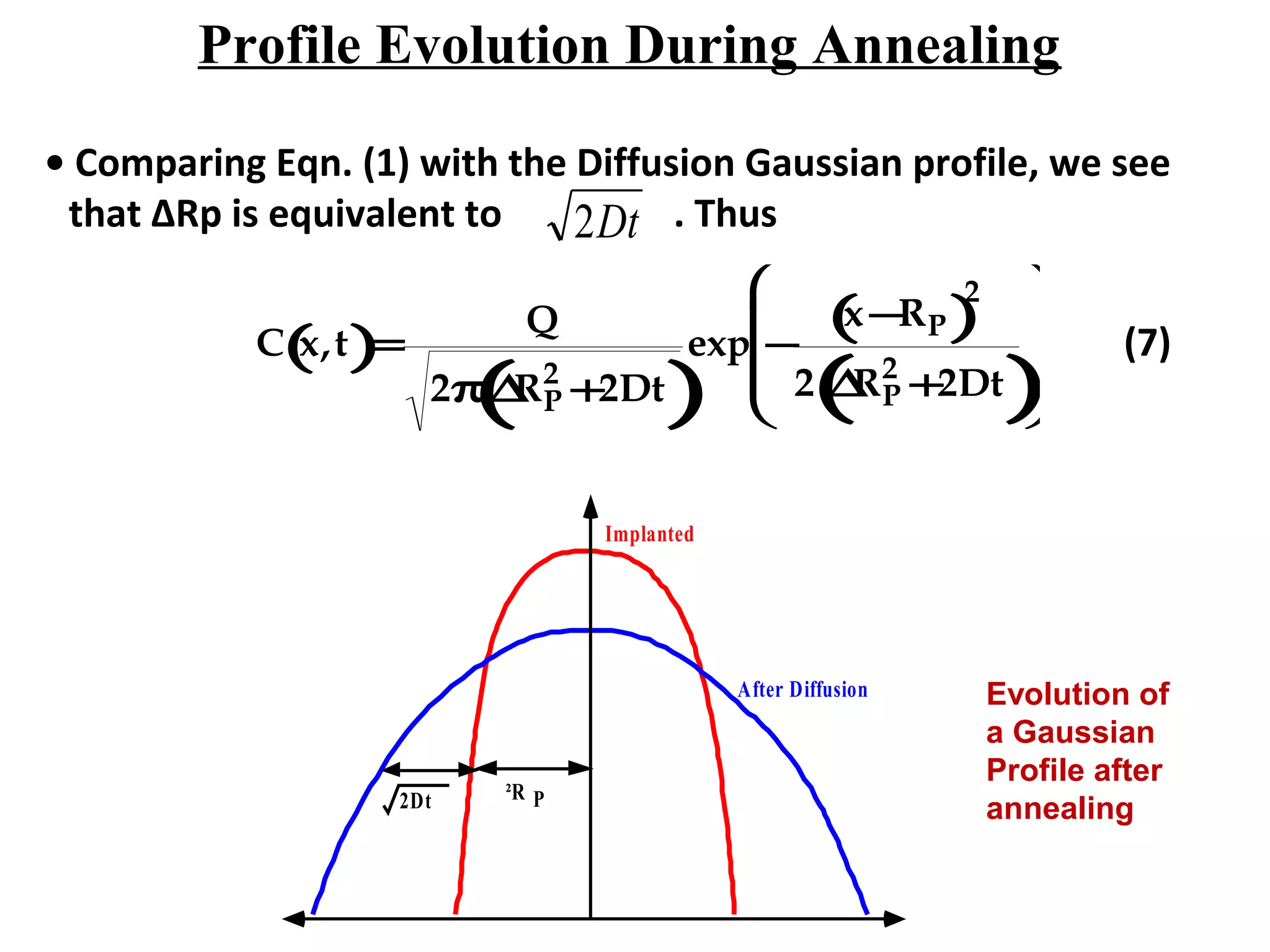
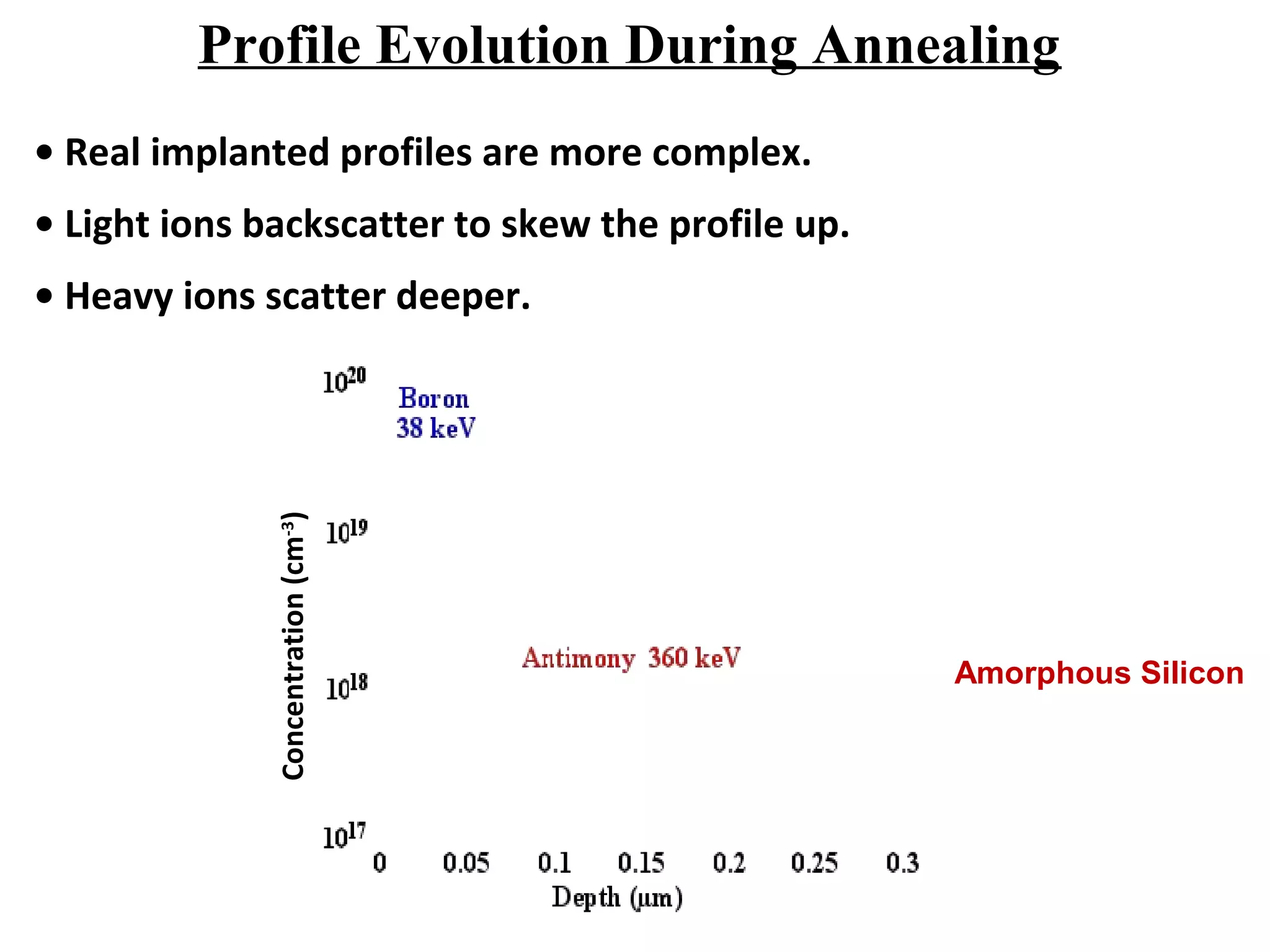
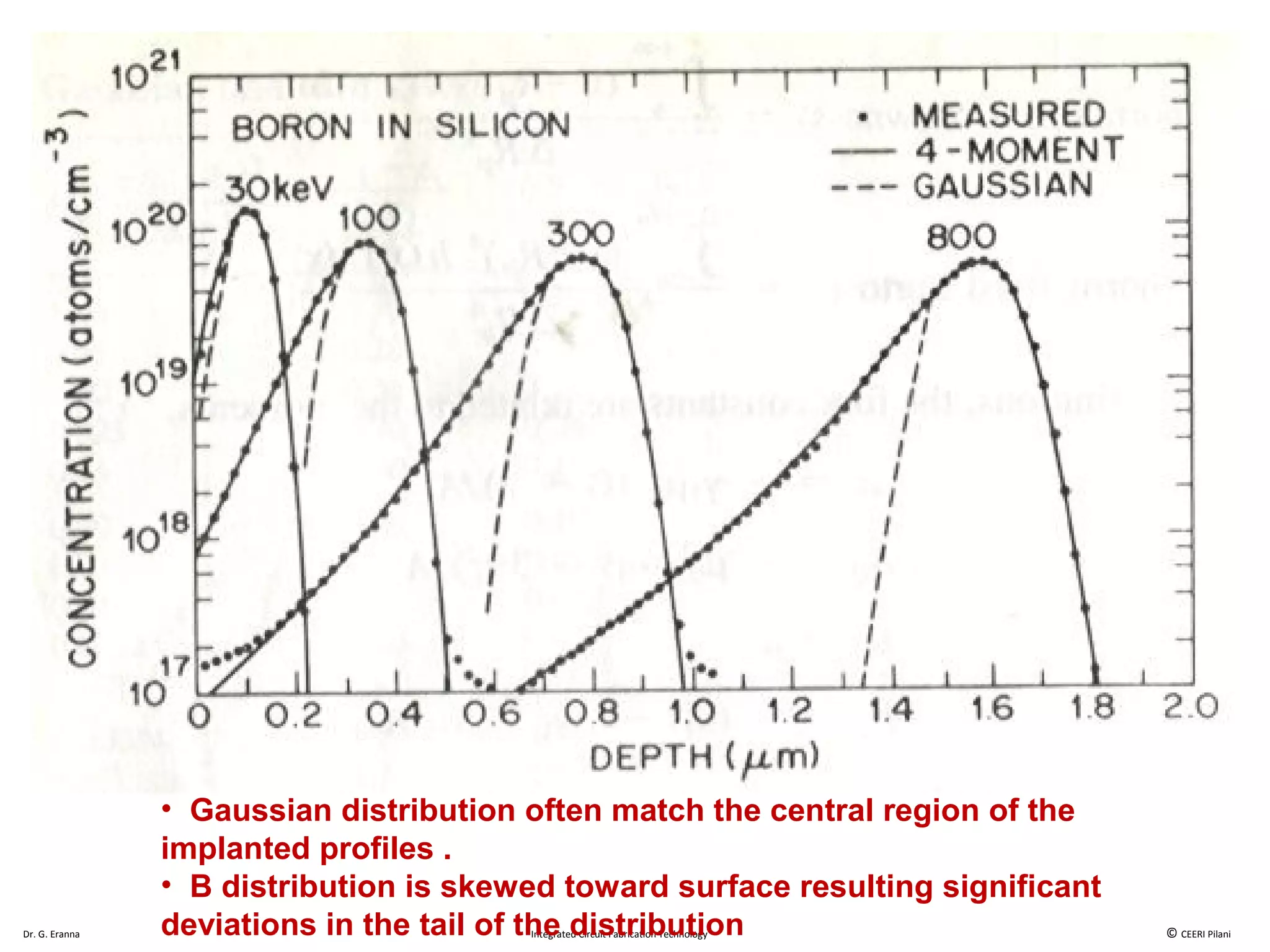
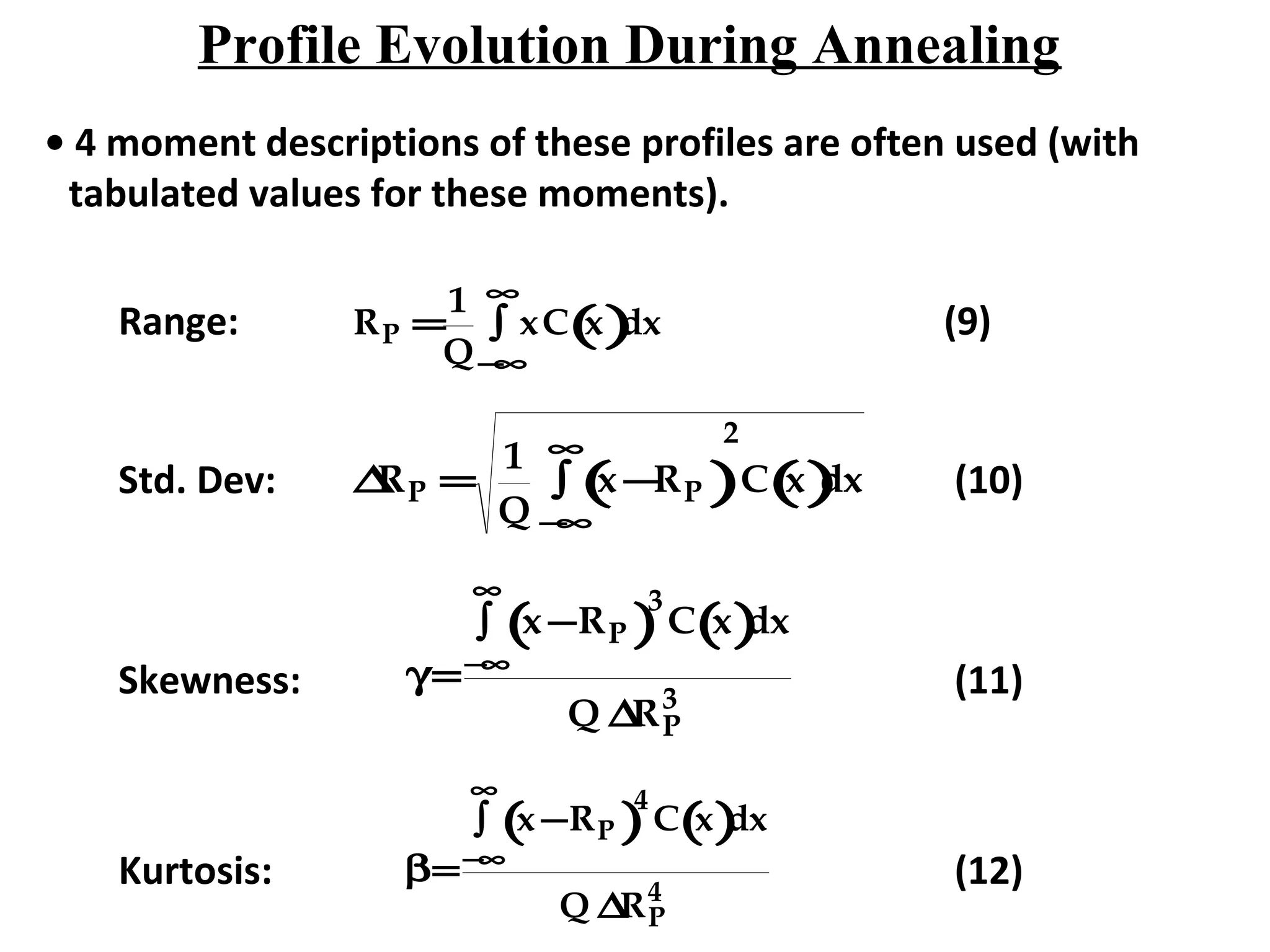
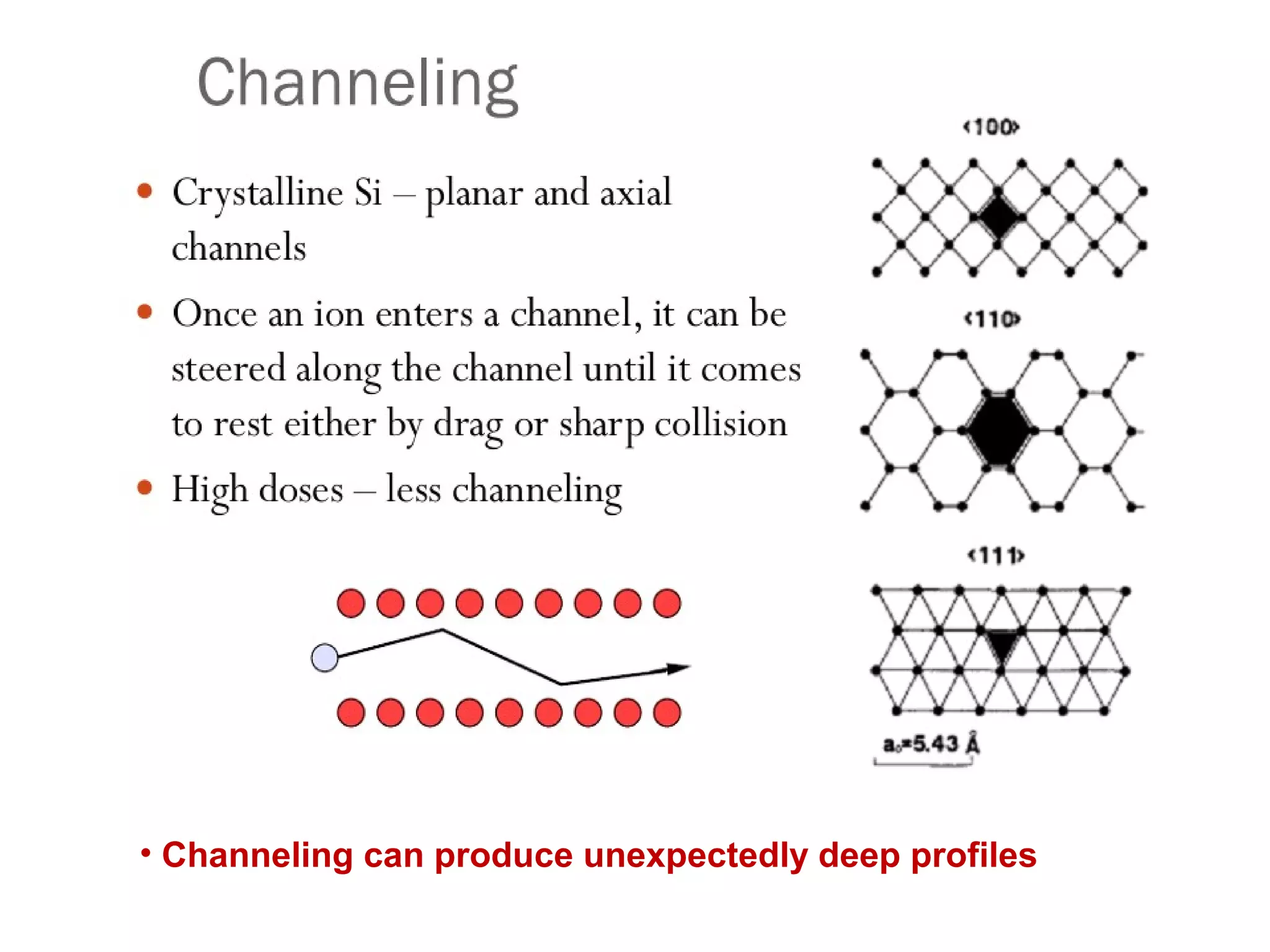
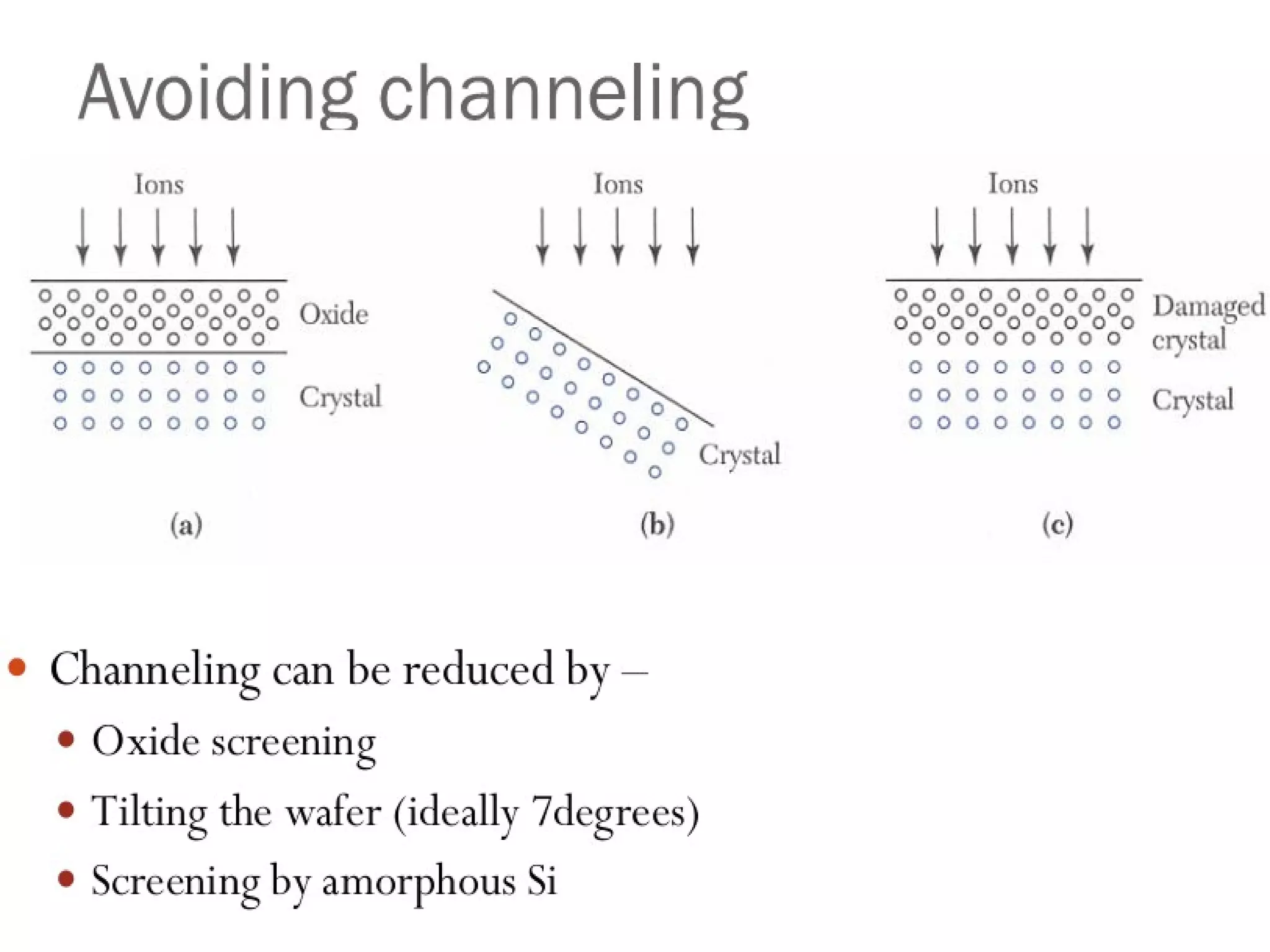
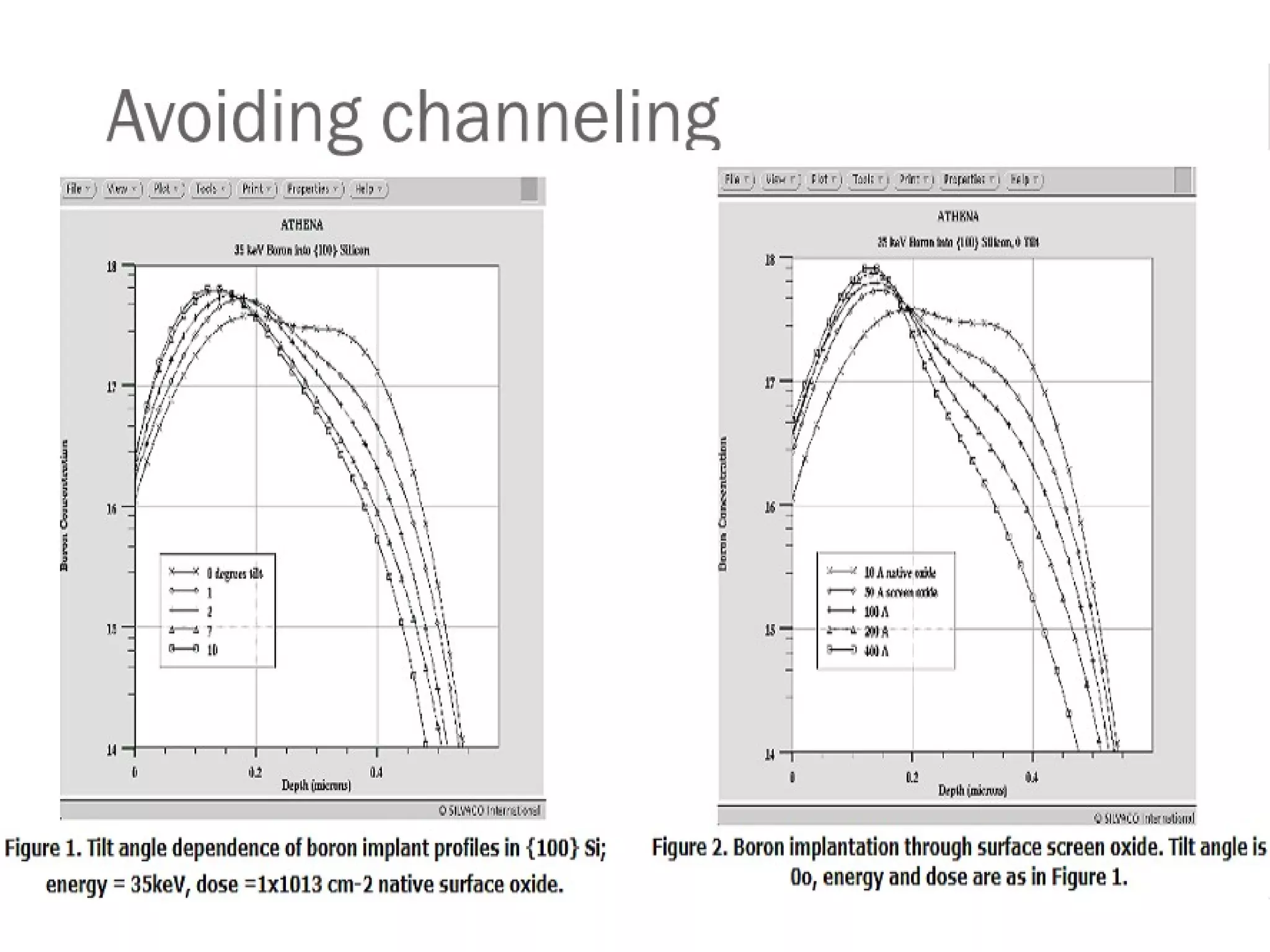
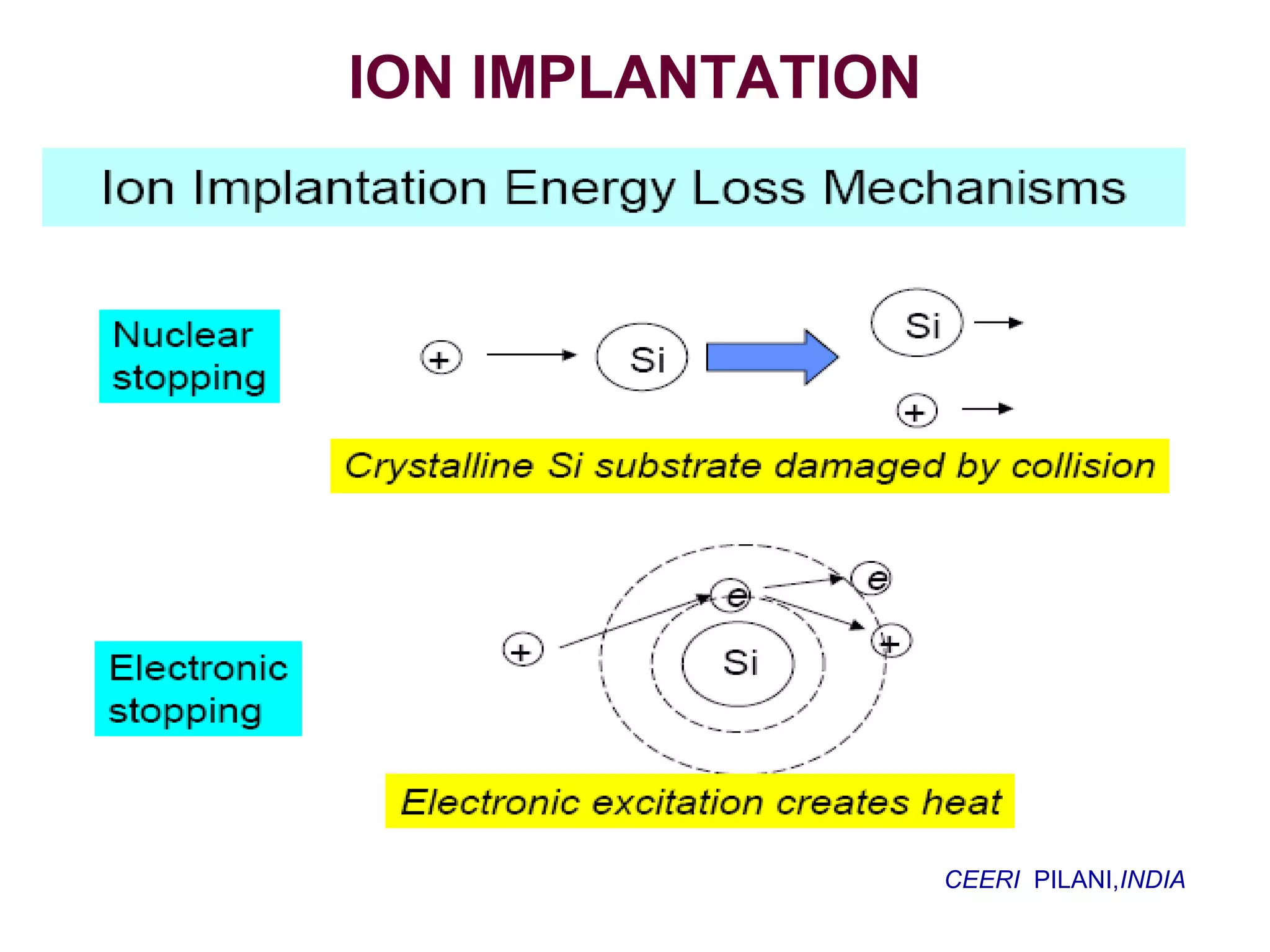
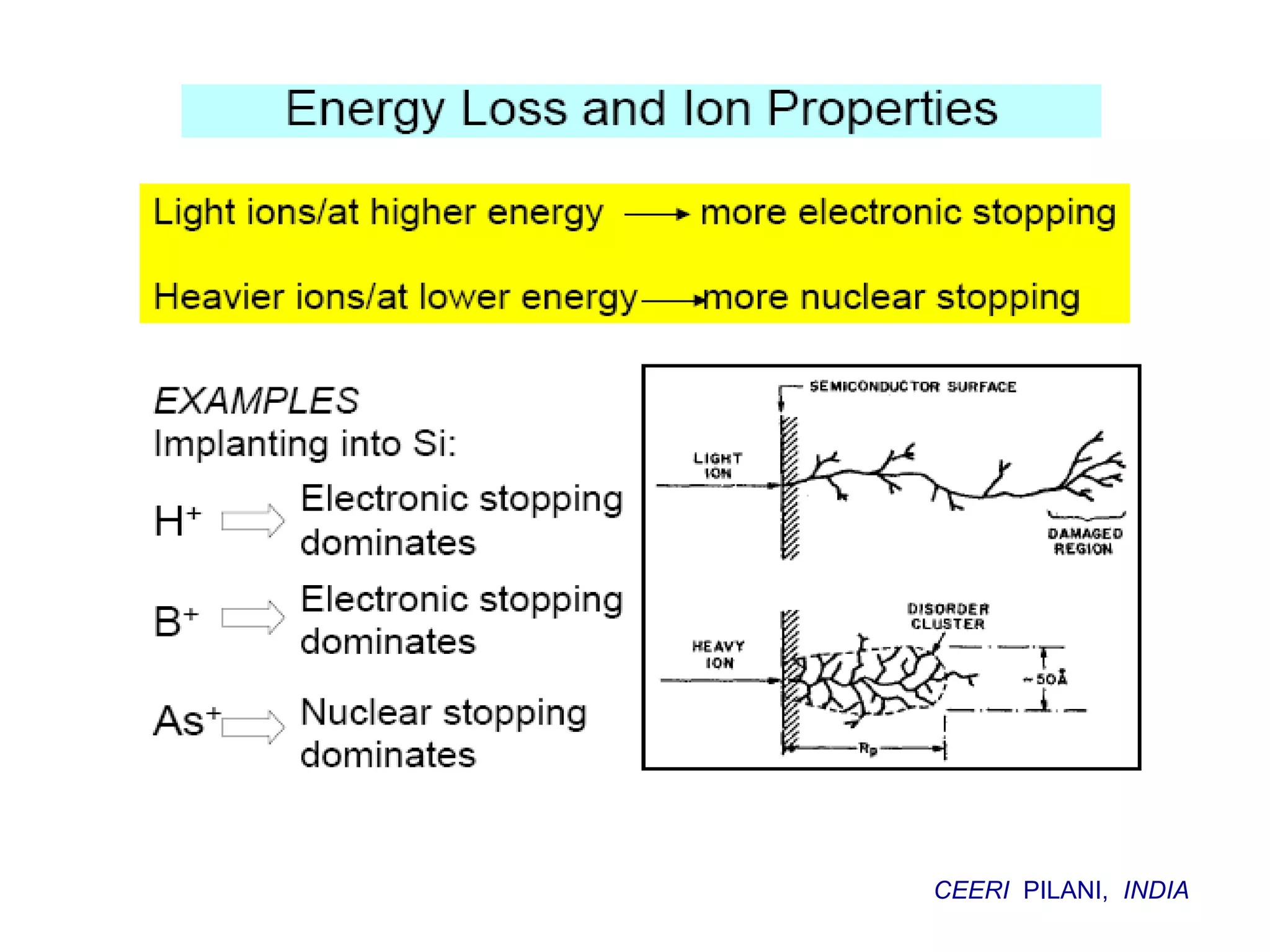
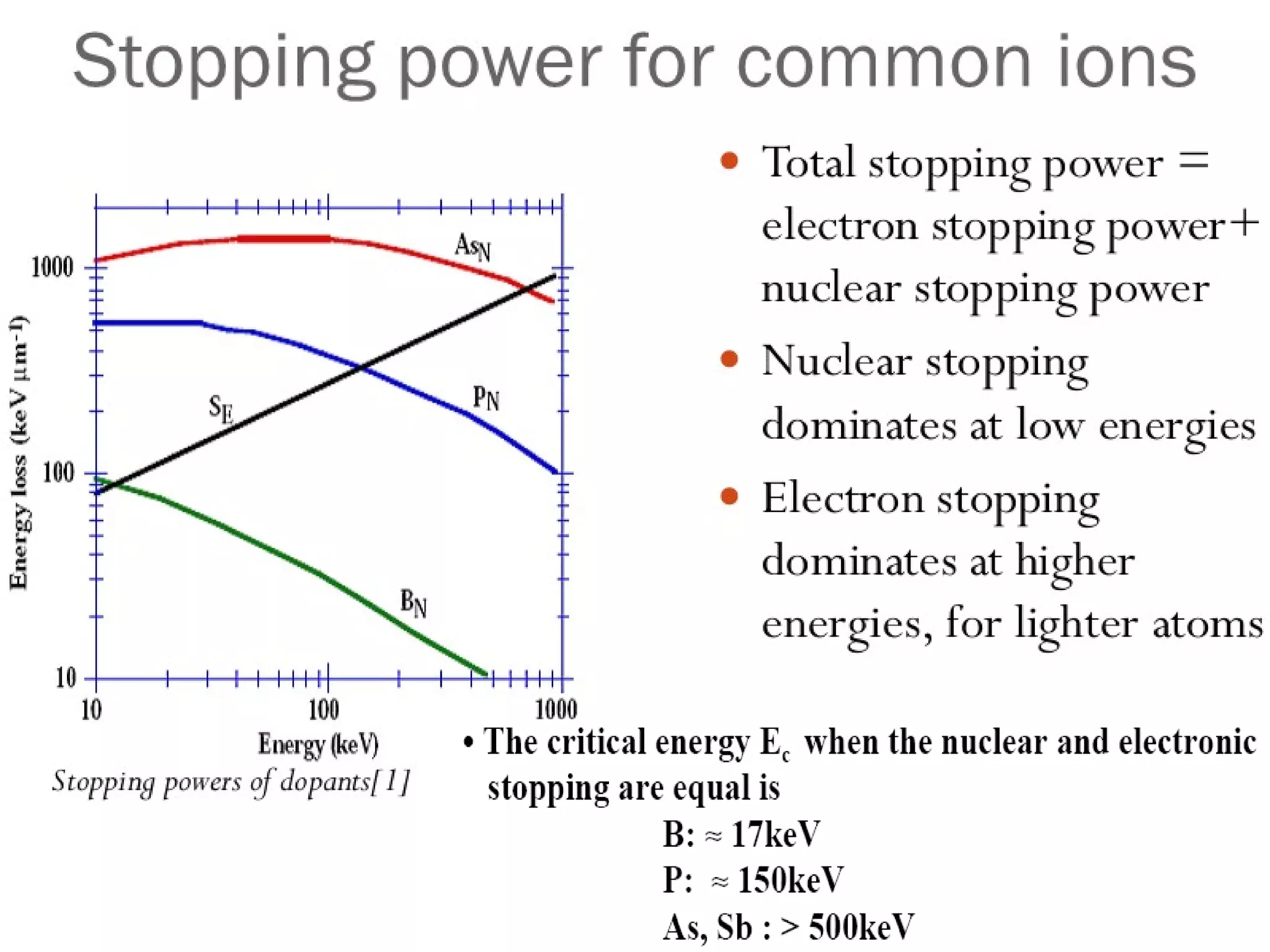
Ion implantation is a process used to introduce impurity atoms into a crystalline substrate to modify its electronic properties. Ions are accelerated to high energies and bombard the silicon surface, penetrating the lattice and becoming embedded. It allows for extremely accurate control of the dopant dose and distribution. However, it is a complex process that can damage the semiconductor and require annealing. The distribution of implanted ions is typically Gaussian but is affected by backscattering and channeling effects. During annealing, the profile will diffuse but the initial profile complexity must be properly modeled.
More Related Content
Similar to 8.1. microtech ion implant,1,2
8.1. microtech ion implant,1,2
- 1.
- 2. Ion Implantation Process bywhich energetic impurity atoms can be introduced into single crystal substrate in order to change its electronic properties.
- 3. Ion Implantation andControlled Doping of Impurities In this process the ions are accelerated to high energies and allowed to impact the silicon surfaces. Because of inherent energy they penetrate into the lattice and are placed inside the silicon lattice. Dr. G. Eranna Integrated Circuit Fabrication Technology © CEERI Pilani
- 4. Advantages Extremely accurate dosecontrol Tailor made and well controlled doping profile large range-of doses-1011 to 1016 /cm2 Low Temperature process Wide choice of masking materials (Oxide, PR, Metal) Clean environment (Mass separation, vacuum) Non-Equilibrium process (conc. Excess of S.S. limit) Ion Implantation
- 5. Disadvantages • Highly sophisticatedand costly. • Damage to semiconductor. • Dopant redistribution during Annealing • Charging of insulating layers. • Photoresist heating and hard to strip.
- 6. Ion Implantation System V V Ion source Analyzingmagnet Pump Resolving aperature Accelerator Focus Neutral beam gate Neutral trap X & Y scan plates Wafer Faraday cup Q0-30keV 0-200keV
- 7.
- 8. Dr. G. ErannaIntegrated Circuit Fabrication Technology © CEERI Pilani Ion Implanter
- 9. Implant Profiles • Atits heart ion implantation is a random process. • High energy ions (1-1000 keV) bombard the substrate and lose energy through nuclear collisions and electronic drag forces. Range R Projected range RP Vacuum Silicon •The projected range describes the peak of the implanted profile
- 11. Implant Profiles • Profilescan often be described by a Gaussian distribution, with a projected range and standard deviation. (200keV implants shown.) C(x) =CP exp − x−RP( ) 2 2∆RP 2 1021 1020 1017 1019 1018 Concentration(cm-3) 0 0.2 0.4 0.6 0.8 1 Depth (µm) Sb As P B 0.606CP ∆RP RP Q = C x() −∞ ∞ ∫ dx Q =2π∆RP CP (1) (2) or where Q is the dose in ions cm-2 and is measured by the integrated beam current.
- 12.
- 13.
- 14. Implant Profiles Ranges andstandard deviation ∆Rp of dopants in randomly oriented silicon
- 15. Implant Profiles • MonteCarlo simulations of the random trajectories of a group of ions implanted at a spot on the wafer show the 3-D spatial distribution of the ions. (1000 phosphorus ions at 35 keV.) Implant Beam x y z 80 40 0 -40 0 50 -100 -50 0 40 80 120
- 16. Implant Profiles • Sideview shows depth distribution Rp and ∆Rp while the beam direction view shows the lateral straggle. z Beam direction 80 40 0 -40 y 050100 -100-50 y -40 0 40 80 x Side view 0 40 80 120
- 17. Implant Profiles • Thetwo-dimensional distribution near window edge is often assumed to be composed of just the product of the vertical and lateral distributions. C x,y( )=Cvert x()exp − y2 2∆R⊥ 2 (3) • Now consider what happens at a mask edge - if the mask is thick enough to block the implant, the lateral profile under the mask is determined by the lateral straggle. • The description of the profile at the mask edge is given by a sum of point response functions with Gaussian form of Eq (3) above.
- 18. Masking Implants • Howthick does a mask have to be? • For masking, C* xm( )=CP * exp − xm −RP * ( ) 2 2∆RP * 2 ≤CB CP * RP * Depth xm C*(xm)CB Concentration (4) For an efficient masking, the thickness of the mask should be large enough that the tail of implant profile in Si is at some specified background conc. Qp
- 19. Masking Implants • SettingC*(xm)= CB and solving for the required mask thickness, xm =RP * +∆RP * 2ln CP * CB =RP * +m∆RP * (5) • The dose that penetrates the mask is given by QP = Q 2π∆RP * exp− x−RP * 2∆RP * xm ∞ ∫ 2 dx = Q 2 erfc xm −RP * 2 ∆RP * (6) • Parameter m indicates that the mask thickness should be equal to the range + some multiple m times the standard deviation in masking material Since the integral or sum of Gaussian function can be described as an error function
- 20. Profile : Hightilt Angle • Real structures may be even more complicated because mask edges are not vertical. • High tilt angle implant for halo doping to minimize short channel effect 30DegreeTilt Distance(µm) Distance(µm) 30Þtilt 0 0.2 0.4 0.6 0.8 1.0 0.2 0 -0.2 -0.4 TSUPREM 50Kev P
- 21. Profile Evolution DuringAnnealing • The only other profile we can calculate analytically is when the implanted Gaussian is shallow enough that it can be treated as a delta function and the subsequent anneal can be treated as a one-sided Gaussian. (Recall example in Dopant Diffusion ) DeltaFunction DoseQ (Initial Profile) Imaginary DeltaFunction DoseQ Diffused Gaussian Virtual Diffusion x 0 C x,t( )= Q πDt exp − x2 4Dt (8)
- 22. Profile Evolution DuringAnnealing • Comparing Eqn. (1) with the Diffusion Gaussian profile, we see that ∆Rp is equivalent to . ThusDt2 C x,t( )= Q 2π∆RP 2 +2Dt( ) exp − x−RP( ) 2 2 ∆RP 2 +2Dt( ) (7) ²R P Implanted After Diffusion 2Dt Evolution of a Gaussian Profile after annealing
- 23. Profile Evolution DuringAnnealing • Real implanted profiles are more complex. • Light ions backscatter to skew the profile up. • Heavy ions scatter deeper.Concentration(cm-3 ) Amorphous Silicon
- 24. Dr. G. ErannaIntegrated Circuit Fabrication Technology © CEERI Pilani • Gaussian distribution often match the central region of the implanted profiles . • B distribution is skewed toward surface resulting significant deviations in the tail of the distribution
- 25. Profile Evolution DuringAnnealing • 4 moment descriptions of these profiles are often used (with tabulated values for these moments). Range: RP = 1 Q xC x() −∞ ∞ ∫ dx Std. Dev: ∆RP = 1 Q x −RP( ) −∞ ∞ ∫ 2 C x()dx Skewness: γ= x −RP( ) 3 C x( )dx −∞ ∞ ∫ Q ∆RP 3 Kurtosis: β= x −RP( ) 4 C x( )dx −∞ ∞ ∫ Q ∆RP 4 (9) (10) (11) (12)
- 26. • Channeling canproduce unexpectedly deep profiles
- 27. Implants in RealSilicon - Channeling • Channeled profile is composed of two portions. Main peak+ channeled part. Accurate modeling requires additional parameter to specify the ratio of the dose in main &channeled profile • Note that the channeling decreases in the high dose implant (green curve) because damage blocks the channels. B Implant: <100> Zero Tilt 35KeV
- 30.
- 31. Non-Local and LocalElectronic Stopping Dielectric Medium Retarding E-field • Drag force caused by charged ion in “sea” of electrons (non-local electronic stopping). • Collisions with electrons around atoms transfers momentum and results in local electronic stopping.
- 33.