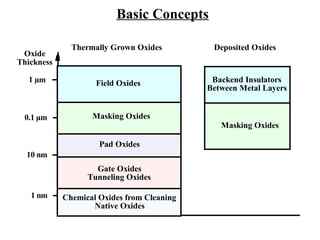
Thermal oxidation is a process used to grow silicon dioxide films on silicon substrates. It involves heating silicon in an oxygen-containing environment to form a stable silicon-dioxide layer. The growth rate of the oxide layer follows a Deal-Grove model based on diffusion and reaction kinetics. While this model accurately describes thicker oxide growth, additional terms are needed to model the initially faster growth rate of very thin oxides. The oxidation rate depends on factors like temperature, oxidizing ambient, crystal orientation, and dopant concentration.

1. Microelectronic Technology
Thermal Oxidation

2. Thermal Oxidation
• A Process to grow high quality silicon
di oxide film by thermally oxidizing
silicon in oxygen containing ambient.

3. Basic Concepts

4. Basic Concepts
10 nm
0.1 µm
1 µm
1 nm
Masking Oxides
Gate Oxides
Tunneling Oxides
Field Oxides
Pad Oxides
Chemical Oxides from Cleaning
Native Oxides
Thermally Grown Oxides
Oxide
Thickness
Deposited Oxides
Backend Insulators
Between Metal Layers
Masking Oxides

5. Basic Concepts
• SiO2 and the Si/SiO2 interface are the principal reasons
for silicon’s dominance in the IC industry.
SiO2 Properties
• Easily selectively etched using lithography.
• Masks most common impurities (B, P, As, Sb).
• Excellent insulator ( ).
• High breakdown field ( )
• Excellent junction passivation.
• Stable bulk electrical properties.
• Stable and reproducible interface with Si.
• No other known semiconductor/insulator combination
has properties that approach the Si/SiO2 interface.
ρ>1016
Ωcm, Eg >9 eV
107
Vcm-1

6. Future Projections for Silicon Technology (SIA
NTRS)
Year of 1st DRAM
Shipment
1997 1999 2003 2006 2009 2012
Minimum Feature Size (nm) 250 180 130 100 70 50
DRAM Bits/Chip 256M 1G 4G 16G 64G 256G
Minimum Supply Voltage
(volts)
1.8-2.5 1.5-1.8 1.2-1.5 0.9-1.2 0.6-0.9 0.5-0.6
Gate Oxide Tox
Equivalent
(nm)
4-5 3-4 2-3 1.5-2 <1.5 <1.0
Thickness Control (% 3s ) ± 4 ± 4 ± 4-6 ± 4-8 ± 4-8 ± 4-8
Equivalent Maximum E-
field (MV cm-1
)
4-5 5 5 >5 >5 >5
Gate Oxide Leakage
(DRAM) (pA m m-2
)
<0.01 <0.01 <0.01 <0.01 <0.01 <0.01
Tunnel Oxide (nm) 8.5 8 7.5 7 6.5 6
Maximum Wiring Levels 6 6-7 7 7-8 8-9 9
Dielectric Constant, K for
Intermetal Insulator
3.0-4.1 2.5-3.0 1.5-2.0 1.5-2.0 <1.5 <1.5

7. Dr. G. Eranna Integrated Circuit Fabrication Technology © CEERI Pilani
Basic Oxidation Process

8. Basic Concepts
• Oxidation involves a volume expansion (≈ 2.2X).
• Oxide layers grown on silicon has compressive stress.
1
1
1.3
1
1
1
1.2
1
1
1
1.3
1.3
Si substrate Si substrate
(a) Actual Silicon
(b) Converted Silicon into Silicon Dioxide
(c) Readjustment of Silicon Dioxide to Original Geometry
(a) (b) (C)

9. Basic Concepts
SiO2
Deposited Polysilicon
Si Substrate
Original Si SurfaceVolume
Expansion
Location of Si3N4 Mask
• Oxidation Involves volume expansion ( 2.2X)
• Especially in 2D &3D structures,stress effects play a dominant role
SEM Cross Sectional View of LOCOS

10. Dr. G. Eranna Integrated Circuit Fabrication Technology © CEERI Pilani
TEM Image of
Si/SiO2 interface
Grown Oxide

11. Chlorine Oxidation Process
Si (Solid) + HCl+ O2 --- SiO2 (Solid) + H2 + Cl2 (3)
Other Chlorine bearing species like
TCE ( C2HCl3) , Trichloroethane (C2H3Cl3)
Oxides are Grown by:
Dry Oxidation Process
Si (solid) + O2  SiO2 (solid) at high temperatures (1)
Wet Oxidation Process
Si (solid) + 2H2O  SiO2 (solid) + 2H2 ↑ at high temperature (2)
Dr. G. Eranna Integrated Circuit Fabrication Technology © CEERI Pilani

12. Basic Concepts
• Oxidation systems are conceptually very simple.
• In practice today, vertical furnaces, RTO systems and fast ramp
furnaces all find use.
Quartz
Tube
Wafers
Quartz Carrier
Resistance Heating
H2O2

13. Oxide
C
I
CG
CO
CS
CI
xO
Gas
0.01 - 1 µm 500 µm
Silicon
F1
F2 F3
SiO2 Growth Kinetics
Deal -Grove Model
Where, (CG - CS) is oxidant concentration difference between main gas flow
and oxide surface.
CO and CI are the oxidant concentration at just inside the oxide
surface and SiO2/Si interface respectively.

14. F1 =hG CG −CS( ) (3)
Deal Grove Model
The flux representing the transport of oxidant in the gas phase to the oxide
surface,
Where, hG is mass transfer coefficient
Oxidant conc. just inside oxide surface CO is given as by Henry’s Law
CO = HPS
Where, PS is the partial pressure of species at the solid surface but not known
experimental parameter so,
The oxidant concentration in the oxide, C* is given as
C* = HPG
Where, PG is the bulk gas pressure
(4)
(5)

15. Deal Grove Model
From the ideal gas law,
CG = PG / kT and CS = PS / kT
By substituting equations 4, 5 and 6 in equation 3, we get
F1 = h (C* - CO)
Where, h = hG / HkT
(6)
(7)
The flux representing the diffusion of oxidant through the oxide to the SiO2/Si
interface is given by Fick’s law,
F2 =D
∂N
∂x
=D
CO −CI
xO





 (8)
Where, D is the oxidant diffusivity in the oxide
The flux representing the reaction at SiO2/Si interface is given as
F3 =kSCI (9)
Where, kS is the interface reaction rate constant

16. • Under steady state conditions, F1 = F2 = F3 so combining
eqs.( 7-9)
CI =
C*
1 +
kS
h
+
kSxO
D
≅
C*
1 +
kSxO
D
(10)
CO =
C*
1 +
kSxO
D






1 +
kS
h
+
kSxO
D
≅C*
(11)
• Note that the simplifications are made by considering h very
large as compared to kS which is a very good approximation.
Deal Grove Model

17. • Combining (9) and (10), we have the growth rate,
dx
dt
=
F
N1
=
kSC*
N1 1 +
kS
h
+
kSxO
D






(12)
• Integrating this equation, results in the linear parabolic model.
xO
2
−xi
2
B
+
xO −xi
B/ A
=t (13)
where (parabolic rate constant)B =
2DC*
N1
B
A
=
C*
N1
1
kS
+
1
h






≅
C*
kS
N1
(linear rate constant)and
(14)
(15)
Deal Grove Model
Where, N1 is the number of oxidant molecules incorporated per unit volume
of oxide grown.

18. τ=
xi
2
+Axi
B
τ+=+ t
AB
x
B
x OO
/
2
It is sometimes convenient to rewrite the linear
parabolic law as follows:
Where,
Two Limiting Forms
Xo= B/A (t+ г) or x2
0=B( t+ г )

19. • (13) can also be written with oxide thickness as a function of
time.
xO =
A
2
1+
t +τ
A2
/ 4B
−1






where τ =
xi
2
+Axi
B
(16)
(17)
• The rate constants B and B/A have physical meaning (oxidant
diffusion and interface reaction rate respectively).
These can be described by Arrhenius expressions as
B =C1 exp −E1 /kT( )
B
A
=C2 exp −E2 /kT( )
(18)
(19)
Deal Grove Model

20. Extraction of Rate Constants

21. Ambient B B/A
Dry O2 C1 = 7.72 x 102
µ2
hr-1
E1 = 1.23 eV
C2 = 6.23 x 106
µ hr-1
E2 = 2.0 eV
Wet O2 C1 = 2.14 x 102
µ2
hr-1
E1 = 0.71 eV
C2 = 8.95 x 107
µ hr-1
E2 = 2.05 eV
H2O C1 = 3.86 x 102
µ2
hr-1
E1 = 0.78 eV
C2 = 1.63 x 108
µ hr-1
E2 = 2.05 eV
• Numbers are for (111) silicon, for (100) divide C2 by 1.68.
Deal Grove Model
Activation Energy
• Diffusivity of oxygen in fused silica: 1.17ev
• Diffusivity of water in fused silica:0.80ev

22. 0.0001
0.001
0.01
0.1
1
10
100
0.65 0.7 0.75 0.8 0.85 0.9 0.95 1
Bµm2
hr
-
1
B/Aµmhr
-
1
1000/T(Kelvin)
800900100011001200
T(ÞC)
B/AH2O
B/ADryO2
BDryO2
BH2O
• Plots of B, B/A using the values in the Table.
Deal Grove Model
Parabolic rate
constant
B =
2DC*
N1
B/A =C*Ks/N1
Linear Rate
constant

23. Deal Grove Model
Calculated oxidation rates
Dry O2 Wet O2
0
0.5
1
1.5
2
0 1 2 3 4 5 6 7 8 9 10
Time - hours
1100 o
C
700 o
C
1000 o
C
900o
C
800 o
C
OxideThicknessµm)
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0 2 4 6 8 10
Time - hours
1200 o
C
1100 o
C
1000 o
C
900 o
C
800 o
C
OxideThickness(µm)
Typical values of oxidant C*= 5x1016
cm-3
Dry O2
Solubility

24. Thin Oxide Growth Kinetics
• A major problem with the Deal Grove model was
recognized when it was first proposed - it does not
correctly model thin O2 growth kinetics.
• Experimentally O2 oxides grow much faster for ≈ 20 nm
than Deal Grove predicts.
• MANY models have been suggested in the literature.

25. 1. Reisman et. al. Model
xO =a t +ti( )
b
or xO =a t +
xi
a






1
b








b
• Power law “fits the data” for all oxide thicknesses.
• a and b are constants & experimentally extracted
parameters and ti time corresponding to growth of any
existing oxide thickness (xi)
• Physically - interface reaction controlled, volume
expansion and viscous flow of SiO2 control growth.

26. 2. Han and Helms Model
dxO
dt
=
B1
2xO +A1
+
B2
2xO +A2
• Two terms representing parallel reaction - “fits the data”
for all oxide thicknesses. (O2&O or oxygen vacancies)
• Three parameters ( A1 values is 0).
• Second process may be out-diffusion of OV and reaction
at the gas/SiO2 interface.

27. 3. Massoud et. al. Model
dxO
dt
=
B
2xO +A
+Cexp −
xO
L






• Second term added to Deal Grove model - higher dx/dt
during initial growth.
• L ≈ 7 nm, second term disappears for thicker oxides.
• Easy to implement along with the DG model; therefore,
used in process simulators.

28. • Data agrees with the Reisman, Han and Massoud
models. (800˚C dry O2 model comparison below.)
Thin Oxide Growth Kinetics
OxideThickness(µm)

29. 8 910 20 30 40 50 60 708090100 200 300 400
0.00
0.02
0.04
0.06
0.08
0.10
0.12
0.14
0.16
0.18
0.20
0.22
Dry Oxidation of Silicon - Orientation Dependency
<100>
<111> Orientation
OxideThickness(Micron)
Oxidation Time (min)
Dr. G. Eranna Integrated Circuit Fabrication Technology © CEERI Pilani

30. Orientation Dependence
• In most oxidation conditions (Dry , Wet)
(111) > (100)
• Difference in the surface density of silicon atoms on the various crystal faces.
• Density of Si - Si bonds
• For very thin oxides grown at very low pressures in dry O2 ( Rapid Oxidation Phase)
• High pressures at low temperatures in wet oxidation (150 Atm) (High Stress)
(110) >(111) > (100)
100111
68.1 





=





A
B
A
B

31. Oxidation Simulation: Orientation Effects
Parameters: 30Min. At 900C in H2O

32. High Pressure Oxidation
The DG model predicts that the oxide growth rate should be
directly proportional to oxidant pressure. Valid for wet oxidation

33. Dopant Segregation
• m= concentration of dopant in
Si/concentration in oxide.
• m<1, oxide accepts dopant. m>1,
oxide rejects dopants
• Boron depletes and phosphorus
accumulates at the oxide/Si
interface
• Segregation is much worse when
oxidation takes place at lower
temperatures
Slow & fast diffusors

34. Dopant Dependence
Boron-doped, Wet oxidation
B segregates into oxide, weakens bond structure, increases D

35. Dopant Dependence
(continued)
Phosphorus-doped
Wet Oxidation Dry Oxidation

36. Oxidation of Heavily Doped Regions
Phosphorus Ion Implant: 20KeV, 5x1015 Cm-2
30Min. In H2O at 800C 5Min.in H2O at 1000C
x5 x2

37. Silicon-Nitride: Oxidation Kinetics
Si3N4 + 6H2O -- 3SiO2 + 6H2 + 2N2
-- 3SiO2 + 4NH3
Kooi Effect
Two Step:
- Si2N2O
- SiO2
LOCOS Structure

38. 2D Effects in Thermal Oxidation
• Variety of shaped
structures including cylinder.
•The oxide is thinner on both
concave and convex corners
than in flat regions

39. 39
.
0 1 2 3 4 5 6 7 8
1/r µm-1
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
NormalizedOxideThickness
Convex Radii
Concave Radii
1200 ÞC
1100 ÞC
1000 ÞC
900 ÞC
800 ÞC
1100 ÞC
1000 ÞC
900 ÞC
1 µm 0.2 µm 0.125 µm
• Several physical mechanisms seem to be
important:
• Crystal orientation
• 2D oxidant diffusion
• Stress due to volume expansion
• Oxide Viscosity
• To model the stress effects, Kao et. al.
suggested modifying the Deal Grove
parameters.
kS (stress) =kS exp −
σnVR
kT





exp −
σtVT
kT






D(stress) =Dexp −
P( )VD( )
kT






C*
(stress) =C*
exp −
P( )VS( )
kT






(20)
(22)
(21)
where and are the normal and
tangential stresses at the interface.
VR, VT and VS are reaction volumes and
are fitting parameters.
(Kao et.al)
σn σ t

41. 8 910 20 30 40 50 60 708090100 200 300 400
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
Dry Process
Wet Process
Temp: 1000
o
C
Comparison Between Dry and Wet Oxidation Processes
OxideThickness(Micron)
Oxidation Time (min)
Dr. G. Eranna Integrated Circuit Fabrication Technology © CEERI Pilani