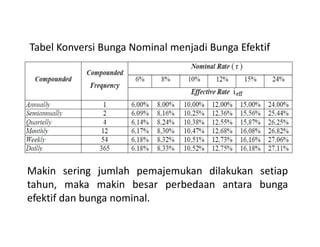
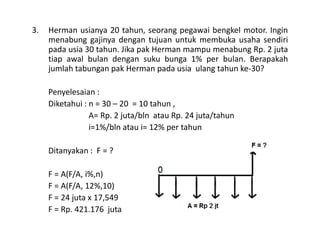
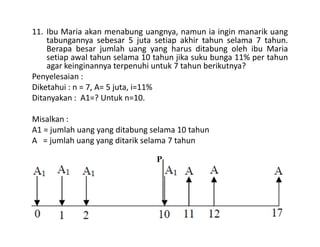
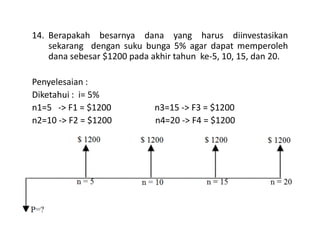
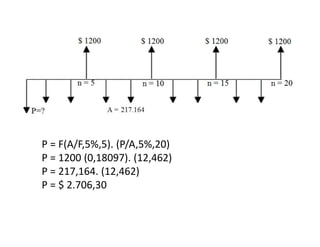
Dokumen ini membahas perhitungan bunga nominal dan bunga efektif, termasuk cara menghitungnya dalam praktik keuangan. Ditemukan bahwa periode pemajemukan dapat dilakukan lebih dari sekali dalam setahun, mempengaruhi perbedaan antara bunga nominal dan efektif. Beberapa contoh praktis disertakan untuk ilustrasi dalam konteks tabungan dan pinjaman.

1. BUNGA NOMINAL
dan
BUNGA EFEKTIFBUNGA EFEKTIF
Simon Patabang, ST., MT.
http://spatabang.blogspot.com

2. Pendahuluan
• Periode bunga atau periode pemajemukan yang telah
dibahas diasumsikan dilakukan 1 kali dalam setahun.
• Namun dalam praktek bisnis nyata, banyak ditemukan
dimana pemajemukan terhadap pokok (principal)
dilakukan lebih dari satu kali dalam setahun.dilakukan lebih dari satu kali dalam setahun.
Contoh :
Bunga tabungan (mis. Tahapan BCA, Taplus BNI, dsb.)
dihitung secara harian, atau saldo tabungan dilakukan
pemajemukan sebanyak 360 kali dalam setahun.

3. Dengan demikian periode pemajemukan
(compounding) sering kali tidak hanya dilakukan
dengan basis tahunan, melainkan dalam periode yang
lebih kecil dari tahunan, seperti :
1. Bunga per 6 bulan (Semiannualy Compounded )1. Bunga per 6 bulan (Semiannualy Compounded )
2. Bunga per 3 bulan (Quartely Compounded )
3. Bunga per bulan (Monthly Compounded )
4. Bunga per mingguan (Weekly Compunded )
5. Bunga Harian (Daily Compounded )

4. Suku Bunga Nominal (Nominal Rate)
Suku bunga nominal (r) merupakan perkalian tingkat suku
bunga i per periode dengan jumlah pemajemukan sebanyak
m kali dalam setahun.
Suku Bunga nominal dinyatakan :
r = i x m atau i = r/mr = i x m atau i = r/m
Contoh :
Jika suku bunga per 6 bulan (semiannualy) 6%, maka suku
bunga nominal per tahunnya adalah r = 6% x 2 = 12%.

5. 2. Suku Bunga Efektif (Effective Rate)
• Adalah suku bunga sesungguhnya dalam satu tahun
yang tepat dibayarkan terhadap sejumlah uang yang
kita simpan atau pinjam.
• Suku bunga efektif dinyatakan dengan persamaan
sbb :sbb :

6. Tabel Konversi Bunga Nominal menjadi Bunga Efektif
Makin sering jumlah pemajemukan dilakukan setiap
tahun, maka makin besar perbedaan antara bunga
efektif dan bunga nominal.

7. Contoh :
1. Sebuah Bank memberikan suku bunga sebesar 1,5% per
bulan pada saldo tabungan nasabah. Berapakah suku
bunga nominal dan efektif per tahunnya ?
Jawab
Diketahui : i= 1,5% /bln, m=12Diketahui : i= 1,5% /bln, m=12
Ditanyakan : r, ieff ?
• Suku Bunga Nominal r = 1,5% x 12 = 18% per tahun
• Suku Bunga Efektif i = (1+0,18/12)¹² - 1 = 19,56% per
tahun

8. 2. Sebuah koperasi memberikan pinjaman dengan
cara menambahkan 7% pada modal pinjaman.
Kemudian nasabah akan membayar pinjaman
sebesar 1/12 dari dari modal tersebut setiap akhir
bulan selama setahun. Jika nasabah meminjam Rp.
1 juta, maka Hitunglah :1 juta, maka Hitunglah :
a. Cicilan per bulan
b. Tingkat Suku bunga/bulan
c. Bunga nominal dan efektif per tahun

9. Penyelesaian :
Diketahui : P = 1 juta, n = 12
Ditanyakan : A , I, r, iff
a. P = P + Px7%
P = 1 juta + 1 juta x 0,07
P = Rp. 1.070.000P = Rp. 1.070.000
Aturan koperasi : A = P x 1/12
A = 1.070.000/12 = Rp. 89,167 / bln
Cicilan per bulan = Rp. 89,167

10. b. A = P (A/P,i%,n)
89,167 = 1.000.000 (A/P,i%,12)
(A/P,i%,12) = 0.0891667, Cari i di tabel?
Dari tabel tidak ditemukan nilai 0,0891667, maka kita
menggunakan pendekatan interpolasi linier dengan
persamaan :
1 2 1y y y y− −
=
Dari tabel diperoleh nilai terdekat yang ada di bawah dan di
atas 0,0891667 (x). Maka kita dapatkan sbb :
untuk i1 = 1% (y1) (A/P,1%,12) = 0,08885 (x1)
untuk i2 = 2% (y2) (A/P, 2%,12) = 0,09456 (x2)
1 2 1
1 2 1x x x x
=
− −

11. Konsep Interpolasi Linier
Interpolasi linier adalah metode pendekatan dengan
menggunakan fungsi garis lurus untuk menentukan titik-
titik yang terletak di antara 2 buah titik

12. Persamaan garis lurus antara 2 titik P1(x1,y1) dan
P2(x2,y2) yang melalui titik Q(x,y) adalah :
Sehingga diperoleh persamaan dari interpolasi linier :
1 2 1
1 2 1
y y y y
x x x x
− −
=
− −
Sehingga diperoleh persamaan dari interpolasi linier :
Dengan pendekatan interpolasi linier, maka suku bunga
i dapat dihitung sbb :
2 1
1 1
2 1
( )
y y
y x x y
x x
−
= − +
−

13. 2 1
1 1
2 1
( )
y y
y x x y
x x
−
= − +
−
diketahui : y1 = 1% x1 = 0,088849
y2 = 2% x2 = 0,09456 ,
Berapakah y = ? Jika x = 0,0891667
Jadi suku bunga per bulan adalah 1,0556%
0,02 0,01
(0,0891667 0,088849) 0,01
0,088849 0,0
0,010556
9456
y
y
−
= − +
−
=

14. b. Jadi tingkat suku bunga nominal per tahun adalah
r = 12 x 1,0556 % = 12,6672 %/tahun
c. Tingkat suku bunga efektif per tahun adalah :
I eff = (1 + 1,0556 %)¹² - 1
Ieff = 0.203558 atau 20,36 % per tahun

15. 3. Ibu Ani membeli sebuah Motor dengan harga Rp. 17
juta. Namun dia membayar uang muka sebesar Rp. 7
juta dan sisanya dicicil Rp. 550 ribu per bulan selama 2
tahun. Berapa suku bunga nominal yang akan dikenakan
terhadapnya ?
Penyelesaian :
Diketahui :
Pharga = Rp. 17 juta, Pmuka = Rp. 7 juta,
A=550 ribu/bln, n = 2 tahun = 24 bulan.
Ditanyakan : r ?

16. P = Pharga - Pmuka
P = 17 juta – 7 juta = Rp. 10 juta
P = A(P/A,i,n)
10 juta = 550 rb x (P/A,i,24)
(P/A,i,24) = 18.18182(P/A,i,24) = 18.18182
Tidak ada di tabel, maka gunakan Interpolasi
Dari tabel diperoleh :
r1 = 2% -> (P/A,2%,24) = 18,914
r 2= 2,5 % -> (P/A,2,5%,24) = 17,885

17. dimana :
x1= 18,914 y1=0,02
X2 = 17,885 y2 = 0,025 x = 18,18182
Hasilnya diperoleh : r=0,023457 atau 2,345694% /bulan
Jadi :Jadi :
Suku bunga nominal = 12 x 2,345694%
= 28,15 %/ tahun
Suku bungan efektif = (1 + 0,2814/12)¹² - 1
= 32,08%/tahun

18. Latihan Soal

19. 1. Pak Amir menginvestasikan uangnya sebesar $1.000 dengan
suku bunga majemuk 6% pada awal tahun 1977. Berapakah
hasil investasinya pada akhir 1987?
Penyelesaian :
Diketahui : P = $1.000, n= 10, i=6%
Ditanyakan : F = ?Ditanyakan : F = ?
F = P(F/P,i%,n)
F= 1000 (F/P,6%,10)
F = 1000 x 1.7908
F = $1.790,8

20. 2. Berapakah dana yang harus diinvestasikan oleh Ibu Helen,
sekarang ini jika dia ingin mendapatkan dana sebesar 500
juta pada 6 tahun yang akan datang, apabila suku bunga yang
berlaku 6%.
Penyelesaian :
Diketahui : F = Rp. 500 juta, n =6, i = 6%
Ditanyakan P = ?Ditanyakan P = ?
P = F (P/F,i%,n)
P = 500.000.000 x (P/F,6%,6)
P = 500.000.000 x 0,705
P = Rp. 352.500.000

21. 3. Herman usianya 20 tahun, seorang pegawai bengkel motor. Ingin
menabung gajinya dengan tujuan untuk membuka usaha sendiri
pada usia 30 tahun. Jika pak Herman mampu menabung Rp. 2 juta
tiap awal bulan dengan suku bunga 1% per bulan. Berapakah
jumlah tabungan pak Herman pada usia ulang tahun ke-30?
Penyelesaian :
Diketahui : n = 30 – 20 = 10 tahun ,
A= Rp. 2 juta/bln atau Rp. 24 juta/tahun
i=1%/bln atau i= 12% per tahuni=1%/bln atau i= 12% per tahun
Ditanyakan : F = ?
F = A(F/A, i%,n)
F = A(F/A, 12%,10)
F = 24 juta x 17,549
F = Rp. 421.176 juta

22. 4. Ibu Hamida ingin naik Haji pada 7 tahun yang akan datang.
Besarnya biaya Ongkos Naik Haji pada saat itu sebesar Rp. 50
juta. Berapakah besarnya dana yang harus ditabung oleh ibu
Hamida mulai sekarang ini dengan suku bunga yang berlaku
6%.
Penyelesaian :
Diketahui : n = 7 tahun, F = 50 juta, i= 6%Diketahui : n = 7 tahun, F = 50 juta, i= 6%
Ditanyakan : P = ?
P = F(P/F,i%,n)
P = F(P/F,8%,7)
P = 50 juta x 0,665
P = Rp. 53,2 Juta

23. 5. Pak Budi menginvestasikan dananya sebesar Rp. 250 juta
dengan suku bunga 6% pada awal tahun 2000. Berapakah
besar jumlah dananya yang harus diambil setiap akhir tahun
selama 10 tahun, tanpa ada sisanya.?
Penyelesaian :
Diketahui : i=6%, P=250 juta, n=10 tahun
Ditanyakan : F= ?Ditanyakan : F= ?
F = P(F/P,i%,n)
F = P(F/P,6%,10)
F = 250 juta x 1,7908
F = Rp. 447.7 Juta

24. 6. Andi ingin mendepositokan uangnya setiap 3 bulan,
sehingga pada akhir tahun ke 10 ia memiliki uang Rp.
10.000.000,- suku bunga tiap tahun adalah 6 %, berapa
yang harus ia depositokan tiap 3 bulan.
Pemyelesaian :
Diketahui : F = Rp. 10.000.000 , n = 10x4 =40, i = 6/4=1½ %Diketahui : F = Rp. 10.000.000 , n = 10x4 =40, i = 6/4=1½ %
A = F(A/F,i %, n) = 10.000.000 (A/F, 1 ½ ,40)
A = 10.000.000 x 0,01843 = Rp. 184.000
Jadi ANdi harus mendepositokan sebesar Rp. 184.000 tiap 3
bulan.

25. 7. Seorang tukang ojek membeli sepeda motor seharga
Rp. 12.000.000,- dengan uang muka Rp. 1.240.000,- dan
sisanya diangsur selama 48 bulan dengan angsuran
sama. Jika suku bunga 1 % per bulan, hitung besarnya
angsuran tiap bulan.
Penyelesaian:
Diketahui : P = 12.000.000 – 1.240.000 = 11.760.000
N = 48 bulan, i = 1 % / bulanN = 48 bulan, i = 1 % / bulan
Ditanyakan : A = ?
A = P (A/P, i %, n) = 11.760.000 (A/P, i %, 48 )
A = 11.760.000 (0,0263)
A = Rp. 3.092,88
Jadi besar angsuran tiap bulan adalah Rp. 3.092,88

26. 8. Berapa modal yang diinvestasikan sekarang dengan
suku bunga 5%, agar dapat disediakan Rp.
1.200.000 pada tahun ke 5, Rp. 1.200.000 pada
tahun ke 10, Rp. 1.200.000 pada tahun ke 15 dan
Rp.1.200.000 pada tahun ke 20?
Penyelesaian :

27. Diketahui :
n1 = 5, n2 = 10, n3 = 15, n4 = 20
F1 = 1.200.000 , F2 = 1.200.000
F3 = 1.200.000, F4 = 1.200.000, i = 0,05
Ditanyakan : P = ?
P1 = F1 (P/F, 5 %, 5) = 1.200.000 (0,7835) = 940.200P1 = F1 (P/F, 5 %, 5) = 1.200.000 (0,7835) = 940.200
P2 = F2 (P/F, 5 %, 10) = 1.200.000 (0,6139) = 736.700
P3 = F3 (P/F, 5 %, 15) = 1.200.000 (0,4810) = 572.200
P4 = F4 (P/F, 5 %, 20) = 1.200.000 (0,3769) = 452.300
Jadi modal yang harus diinvestasikan adalah:
P = P1 + P2 + P3 + P4 = Rp. 2.706.400

28. Cara langsung :
Karena F1 = F2 = F3 = F4 , maka
P = F (A/F, 5 %, 5) (P/A, 5%, 20)
P = 1.200.000 (0,18097) (12,462)P = 1.200.000 (0,18097) (12,462)
P = Rp. 2.706.300

29. 9. Seseorang mendepositokan uangnya sekarang Rp.
2.000.000, 2 tahun kemudian Rp.1.500.000, dan 4
tahun kemudian Rp. 1.000.000, semua dengan suku
bunga sama yaitu 8 %. Berapakah jumlah total
uangnya pada tahun ke 10.
Penyelesaian :Penyelesaian :

30. Diketahui : n1= 10, n2 = 8, n3 = 6, i=8%
P1 = 2.000.000 , P2 = 1.500.000, P3 = 1.000.000
Ditanyakan : F total = ?
Ftotal = F1 + F2 + F3
F = P1 (P/F, 8 %, 10) + P2 (P/F, 8 %, 8) + P3 (P/F, 8 %, 6)
F = 2.000.000 (2,1589) + 1.500.000 (1,8509) +F = 2.000.000 (2,1589) + 1.500.000 (1,8509) +
1.000.000 (1,5869)
F = 8.681.000
Jadi jumlah total uangnya pada akhir tahun ke 10
adalah Rp. 8.681.000,-

31. 10. Seseorang meminjam uang dari bank Rp. 100.000.000,-
dengan suku bunga 7%/tahun. Pinjaman tersebut harus
diangsur tiap 6 bulan selama 30 tahun dengan jumlah
angsuran yang sama.
a. Berapakah besarnya angsuran tiap 6 bulan
b. Berapa pokok yang telah dibayarkan pada akhir tahun ke
10 (tepat setelah angsuran ke 20 dibayar).
Diketahui : P = 100 juta, i=3,5 % , n=30x2 =60
Ditanyakan : Pbayar pada n=20Ditanyakan : Pbayar pada n=20

32. a. Cicilan per 6 bulan
A = P (A/P, i %, n)
A = 100.000.000 (A/P, 3 ½ %, 60)
A = 4.009.000
Cicilan per 6 bulan sebesar Rp. 4.009.000
Pokok yang belum di bayar pada akhir tahun ke-10 adalah P1
selama 40 kali.
P1 = 4.009.000 (P/A, 3 ½ %, 40)P1 = 4.009.000 (P/A, 3 ½ %, 40)
P1 = 85.612.200
Jadi pokok yang telah dibayar adalah :
Pbayar = P – P1
Pbayar = Rp. 100.000.000 - Rp. 85.612.200
Pbayar = Rp. 14.388.000

33. 11. Ibu Maria akan menabung uangnya, namun ia ingin manarik uang
tabungannya sebesar 5 juta setiap akhir tahun selama 7 tahun.
Berapa besar jumlah uang yang harus ditabung oleh ibu Maria
setiap awal tahun selama 10 tahun jika suku bunga 11% per tahun
agar keinginannya terpenuhi untuk 7 tahun berikutnya?
Penyelesaian :
Diketahui : n = 7, A= 5 juta, i=11%
Ditanyakan : A1=? Untuk n=10.
Misalkan :Misalkan :
A1 = jumlah uang yang ditabung selama 10 tahun
A = jumlah uang yang ditarik selama 7 tahun

34. Karena A diketahui selama n=7 dimulai pada awal tahun
n=10, maka P pada n=10 dapat dihitung.
P10 = A (P/A, 11% , 7)
P10 = 5.000.000 (4,712) = Rp. 23,56 juta
P10 merupakan nilai yang akan datang pada akhir tahun
ke10 untuk pembayaran A1. Jadi P10=F10 diketahui, maka
A1 dapat dihitung selama n=10.
A1 = F10 (A/F, 11% , 10)
A1 = 23,56 (A/F, 11%, 10)
A1 = 23,56 (0,0598)
A1 = Rp. 1,41 Juta
Jadi harus ditabung adalah sebesar Rp. 1,41 Juta tiap tahun

35. 12. Pak Amir ingin naik Haji 5 tahun dari sekarang. Pada
saat keberangkatan, pak Amir membutuhkan uang Rp.
100 juta. Jika Pak Amir menabung sekarang sebesar Rp.
80juta, berapakah suku bunga yang berlaku agar bisa
mendapatkan dana sebesar Rp. 100 juta pada saat
berangkat naik haji?
Penyelesaian :Penyelesaian :
Diketahui : n=5 tahun, F=100 juta, P=80juta
Ditanyakan i = ?
F = P(F/P,i%,n)
100 = 80 (F/P, i%, 5)
(F/P, i%, 5) = 1,250 Cari di tabel

36. Karena tidak ada di tabel, maka gunakan pendekatan
interpolasi.
Untuk :
i= 0,045 (F/P, i%, 5) = 1,2462
I =0,050 (F/P, i%, 5) = 1,2763
Masukkan nilai ke dalam persamaan interpolasi linier.Masukkan nilai ke dalam persamaan interpolasi linier.
i = 0,0456 atau 4,56%
Agar Pak Amir bisa mendapatkan dana sebesar Rp. 100 juta
pada saat berangkat naik haji dengan mulai menabung
sekarang sebesar Rp. 80 juta, maka suku bunga yang
berlaku adalah 4,56% per tahun.

37. 13. Pak Budi melakukan investasi sekarang sebesar Rp. 50
juta dan mengharapkan penerimaan sebesar 7 juta
setiap tahun selama 15 tahun. Berapakah bunga yang
berlaku agar harapan dari investasi pak Budi terpenuhi?
Penyelesaian :
Diketahui : n=15, P= 50juta, A=7 juta,Diketahui : n=15, P= 50juta, A=7 juta,
Ditanyakan i=?
A = P(A/P,i%,n)
7 = 50 (A/P,i%,15) (A/P,i%,n) = 7/50 = 0,1400
Cari nilai dari tabel (A/P,i%,15)

38. untuk :
i=11% (A/P,i%,15) = 0,13907
i=12% (A/P,i%,15) = 0,14682
Dengan interpolasi diperoleh :
i = 0,111 atau 11,1 % per tahun
Agar harapan investasi pak Budi dapat terpenuhi, maka
suku bunga yang berlaku pada saat itu adalah 11,1%
per tahun.

39. 14. Berapakah besarnya dana yang harus diinvestasikan
sekarang dengan suku bunga 5% agar dapat memperoleh
dana sebesar $1200 pada akhir tahun ke-5, 10, 15, dan 20.
Penyelesaian :
Diketahui : i= 5%
n1=5 -> F1 = $1200 n3=15 -> F3 = $1200
n2=10 -> F2 = $1200 n4=20 -> F4 = $1200n2=10 -> F2 = $1200 n4=20 -> F4 = $1200

40. ΣP = P1 + P2 + P3 + P4
P1 = F1(P/F,5%,5) = 1200. (0,7835) = 940,2
P2 = F2(P/F,5%,10) = 1200. (0,6139) = 736,7
P3 = F3(P/F,5%,15) = 1200. (0,4810) = 577,2
P4 = F4(P/F,5%,20) = 1200. (0,3769) = 452,3
------------
$ 2.706,4
Cara II :Cara II :
Karena besarnya F semuanya sama dan intervalnya tetap
yaitu 5 tahun, maka semua F diubah menjadi sebuah seri
ekivalen dari jumlah 5 tahun dan nilai sekarang dengan n
20 tahun.
Atau P/F diubah menjadi A/F. P/A

41. P = F(A/F,5%,5). (P/A,5%,20)
P = 1200 (0,18097). (12,462)
P = 217,164. (12,462)
P = $ 2.706,30

42. Sekian