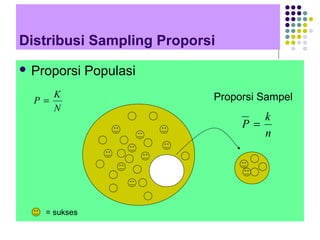
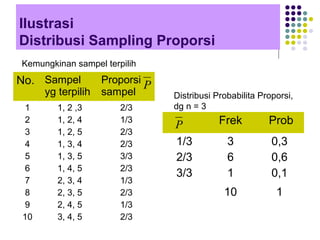
Distribusi sampling memberikan kerangka untuk memahami variasi statistik sampel yang diambil dari populasi. Terdapat berbagai jenis distribusi sampling seperti rata-rata, proporsi, beda rata-rata dan proporsi yang mengikuti distribusi tertentu seperti normal, t student, dan binomial. Pemahaman distribusi sampling penting untuk melakukan inferensi statistik dari sampel ke populasi.

1. Distribusi Sampling
Tujuan Pembelajaran :
Mampu memahami tentang Distribusi
sampling, baik untuk rata-rata,
proporsi, beda 2 rata-rata dan beda 2
proporsi.

2. Distribusi Sampling
Distribusi Sampling adalah
distribusi probabilita dengan statistik sampel
sebagai variabel acaknya.
Statisik sampel antara lain :
X : (rata-rata sampel),
P : (proporsi sampel),
X − X : (Beda 2 rata-rata),
1 2
P −P
1 2 : (Beda 2 rata-rata),

3. Populasi
 Populasiadalah keseluruhan unsur yang
menjadi obyek pengamatan.
 Populasi
finite : populasi yang jumlah
unsurnya (N) terbatas, misalnya : 5, 10, 1000
 Populasi
Infinite : popiulasi yang jumlah
unsurnya tidak terbatas

4. Metode Sampling
 Sampel adalah bagian dari obyek pengamatan
yang akan diteliti.
 Cara memperoleh sampel :
1. Simple Random Sample
2. Stratified Random Sample
3. Cluster Random Sample
4. Systematic Random Sample
5. Non Random Sample

5. Populasi dan Sampel
Populasi
N, μ, P,σ
Proses Sampel
Inferensia n, x, p, s

6. Dalil Limit Pusat
(The Central Limit Theorem) :
 Bila sampel acak berukuran n diambil dari
suatu populasi dengan rata-rata μ dan
deviasi standar σ, maka
 1. µ x = µ σ N −n
σ x=
 2. σ x  populasi terbatas n N −1
σ
populasi besar σx =
n
X −µ
 Sehingga Z=
: σx

7. Distribusi Sampling Rata-rata
 Membuat distribusi Sampling rata-rata sampel
dengan sampel berukuran n = 2 dari suatu populasi
berukuran N = 4 yaitu ( 3, 4, 6, 7)
 Rata-rata dan deviasi standar populasi :
∑x = 3+4+6+7 =5 ∑ (x − µ)
2
µ= σ= = 2,5
N 4 N
 Dengan sampling without replacement, maka
banyaknya kemungkinan sampel yang terjadi
adalah sebanyak : 4!
C2 =
4
=6
2! (4 − 2)!

8. Ilustrasi
Distribusi Sampling Rata-rata
Kombinasi Kemungkinan
Hasil Sampel
Dist Sampling Rata-rata dg n = 2
Nilai Rata-rata
sampel x sampel x Rata-rata Frek- Proba
sampel x wensi bilita
3 4 3,5
3 6 4,5 3,5 1 1/6
3 7 5 4,5 1 1/6
4 6 5 5 2 2/6
4 7 5,5 5,5 1 1/6
6 7 6,5 6,5 1 1/6
30 6 1

9. Ilustrasi
Distribusi Sampling Rata-rata
 Berdasarkan tabel ilustrasi diatas, maka :
30
µX = =5 ternyata µx = μ
6
(3,5 − 5) 2 + (4,5 − 5) 2 + (5 − 5) 2 + (5 − 5) 2 + (5,5 − 5) 2 + (6,5 − 5) 2 5
σX = =
6 6
atau
ternyata
σ N − n 2,5 4 − 2 5 σ N −n
σX = = = σ x=
n N −1 2 4 −1 6 n N −1

10. Contoh soal 1
 Platbaja yg diproduksi oleh sebuah pabrik
baja memiliki daya regang rata-rata 500µ
dan deviasi standar sebesar 20µ jika sample
random yg terdiri dari 100 plat dipilih dari
populasi yg terdiri dari 100.000 plat.
Berapakah probabilita rata-rata sample akan
kurang dari 496µ ?
 Diket: µ = 500 σ =20 n= 100
 N = 100.000 (populasi besar)
 Ditanya: P ( X < 496) ?

11. Jawaban soal 1
 µx = μ = 500
σ 20
σX = = =2
n 100
x − µ x 496 − 500
Z= = = −2
σx 2
496 500 X
Sehingga
-2 0 Z
P ( X < 496) = P (Z < -2) = ?
= 0,5 – 0,4772 = 0,0228

12. Distribusi t Student
 Dalam Dalil Limit Pusat dinyatakan bahwa rata-rata
sampel acak akan mendekati dist normal dengan deviasi
standar σ = σ
X
n
 Akan tetapi jarang sekali nilai σ diketahui, sehingga
biasanya σ diduga dengan deviasi standar sampel s
 Untuk n ≥ 30, nilai-nilai ( X − µ ) /( s / n) masih akan
mendekati dist normal standar (z)
 Untuk n < 30, nilai-nilai ( X − µ ) /( s / n ) akan X −µ
mendekati dist student (t) dengan t=
s
derajat bebas db = n -1 sehingga : n

13. Distribusi Sampling Proporsi
 Proporsi Populasi
K Proporsi Sampel
P=
N
k
P=
n
= sukses

14. Distribusi Sampling Proporsi
 Membuat distribusi Sampling proporsi sampel
dengan sampel berukuran n = 3 dari suatu populasi
berukuran N = 5 yaitu ( 1 2 3 4 5 ) dimana
anggota ke 1 , 3 dan 5 adalah anggota ‘sukses’
 Sehingga Proporsi Populasi :
P (sukses) = 3/5 = 0,6
 Dengan sampling without replacement, maka
banyaknya kemungkinan sampel yang terjadi
adalah sebanyak : 5 5!
C3 = = 10
3!(5 − 3)!

15. Ilustrasi
Distribusi Sampling Proporsi
Kemungkinan sampel terpilih
No. Sampel Proporsi
P
yg terpilih sampel Distribusi Probabilita Proporsi,
1 1, 2 ,3 2/3 dg n = 3
2 1, 2, 4 1/3
P Frek Prob
3 1, 2, 5 2/3
4 1, 3, 4 2/3 1/3 3 0,3
5 1, 3, 5 3/3 2/3 6 0,6
6 1, 4, 5 2/3
3/3 1 0,1
7 2, 3, 4 1/3
8 2, 3, 5 2/3 10 1
9 2, 4, 5 1/3
10 3, 4, 5 2/3

16. Ilustrasi
Distribusi Sampling Proporsi
 Berdasarkan tabel dist sampling proporsi di
atas :
µ P = (1 / 3)(0,3) + (2 / 3)(0,6) + (3 / 3)(0,1) = 0,6
Ternyata : µP = P q=1-p
pq N−n (0,6)(0,4) 5−3
σP = × = × = 0,2
n N −1 3 5−1

17. Distribusi Sampling Proprsi
k
 Bila P= , dimana k menyatakan banyaknya
n
peristiwa sukses dari sampel yang berukuran n
yang besar, maka p akan menyebar normal
dengan :
pq
µP = P dan σP =
n
Maka :
P − µP P− P
Z = =
σP σP

18. Contoh soal 2
 Diketahuibahwa 2% barang kiriman adalah
cacat. Berapa probabilitas bahwa suatu
pengiriman sebanyak 400 barang terdapat
3% atau lebih yg cacat ? P ( P ≥ 0,03) = ?
µ P = p = 2% = 0,02
pq 0,02 x0,98
σP = = = 0,007
n 400 0 1,43
P − P 0,03 − 0,02
Z= = = 1,43
σP 0,007 P (Z>1,43) = 0,5 – 0,4236 = 0,0764

19. Distribusi Sampling Beda 2 Rata-rata
 Bila sampel-sampel bebas berukuran n1 dan n2 diambil
dari dua populasi yang besar dengan nilai tengah μ1
dan μ2 dan dev. standar σ1 dan σ2, maka :
 Beda rata-rata sampel akan menyebar mendekati
distribusi normal dengan :
σ 12 σ 22
µ x1 − x 2 = µ1 − µ 2 dan σ x1 − x2 = +
n1 n2
Shg :
Z =
(x 1 )
− x 2 − ( µ1 − µ1 )
σ x1 − x 2

20. Distribusi Sampling Beda 2 Proporsi
 Bila P − P2 menyatakan beda dua proporsi peristiwa
1
sukses yang diperoleh dari dua sampel acak yang
diambil dari dua populasi yang mempunyai dist. Binom
dengan prob sukses masing-masing, p1 dan p2 , dan
prob gagal q1 dan q2, maka P1 − P2 akan menyebar
normal dengan :
p1q2 p2 q2
µ P 1 − P 2 = P1 − P2 σ P1 − P 2 = +
n1 n2
Shg : Z =
(P − P ) − ( P − P )
1 2 1 2
σ P1 − P 2

21. Latihan Soal 1
 Misalkan rata-rata pendapatan keluarga per
hari di daerah kota adalah 10.000 dengan
deviasi standar 3000 dan rata-rata
pendapatan di daerah pedesaan 4.000
dengan deviasi standar 500. jika diambil
sampel random keluarga kota sebanyak 50
dan keluarga pedesaan sebanyak 200,
berapa probabilitas beda antara pendapatan
keluarga per hari antara kota dan pedesaan
lebih dari 5.000 ?

22. Latihan soal 2
 5% produksi shift pagi cacat dan 10%
produksi shift malam cacat. Bila diambil
sampel random sebanyak 200 barang dari
shift pagi dan 300 barang dari shift malam,
berapa probabilitas beda persentase barang
yang cacat pada shift malam lebih besar 2%
dari shift pagi?

23. Tugas
 Bangkitkan distribusi sampling untuk rata-rata
(berat badan) dan proporsi wanita.
 Ambil data dari kelas anda, sebanyak 7 data
sebagai N populasi dan dari populasi yang
telah anda kumpulkan bangkitkan distribusi
sampling sampel sebesar n = 4
 Dikumpulkan ketika masuk kelas setelah
UTS.