1. คู่มือประกอบสื่อการสอน วิชาคณิตศาสตร์
เรื่อง
จานวนจริง
(เนื้อหาตอนที่ 5)
อสมการ
โดย
ศาสตราจารย์ ดร.กฤษณะ เนียมมณี
สื่อการสอนชุดนี้ เป็นความร่วมมือระหว่าง
คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย กับ
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน (สพฐ.)
กระทรวงศึกษาธิการ

2. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
1
สื่อการสอน เรื่อง จานวนจริง
สื่อการสอน เรื่อง จานวนจริง มีจานวนตอนทั้งหมดรวม 17 ตอน ซึ่งประกอบด้วย
1. บทนา เรื่อง จานวนจริง
2. เนื้อหาตอนที่ 1 สมบัติของจานวนจริง
- ระบบจานวนจริง
- สมบัติพื้นฐานของระบบจานวนจริง
3. เนื้อหาตอนที่ 2 การแยกตัวประกอบ
- การแยกตัวประกอบ
4. เนื้อหาตอนที่ 3 ทฤษฎีบทตัวประกอบ
- ทฤษฎีบทเศษเหลือ
- ทฤษฎีบทตัวประกอบ
5. เนื้อหาตอนที่ 4 สมการพหุนาม
- สมการพหุนามดีกรีหนึ่ง
- สมการพหุนามดีกรีสอง
- สมการพหุนามดีกรีสูง
- การประยุกต์สมการพหุนาม
6. เนื้อหาตอนที่ 5 อสมการ
- เส้นจานวนและช่วง
- อสมการที่เกี่ยวข้องกับพหุนามดีกรีหนึ่ง
- อสมการที่เกี่ยวข้องกับพหุนามดีกรีสูง
7. เนื้อหาตอนที่ 6 เทคนิคการแก้อสมการ
- อสมการในรูปเศษส่วน
- การแก้อสมการโดยวิธีการยกกาลังสอง
- การแก้อสมการโดยการแทนค่าตัวแปร
- การประยุกต์โจทย์การแก้อสมการ
8. เนื้อหาตอนที่ 7 ค่าสัมบูรณ์
- ค่าสัมบูรณ์
- สมการค่าสัมบูรณ์
9. เนื้อหาตอนที่ 8 การแก้อสมการค่าสัมบูรณ์
- อสมการค่าสัมบูรณ์

3. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
2
- โจทย์ประยุกต์อสมการค่าสัมบูรณ์
10. เนื้อหาตอนที่ 9 กราฟค่าสัมบูรณ์
- กราฟค่าสัมบูรณ์
11. แบบฝึกหัด (พื้นฐาน 1)
12. แบบฝึกหัด (พื้นฐาน 2)
13. แบบฝึกหัด (พื้นฐาน 3)
14. แบบฝึกหัด (ขั้นสูง)
15. สื่อปฏิสัมพันธ์ เรื่อง ช่วงบนเส้นจานวน
16. สื่อปฏิสัมพันธ์ เรื่อง สมการและอสมการพหุนาม (กาลังไม่เกินสี่)
17. สื่อปฏิสัมพันธ์ เรื่อง กราฟค่าสัมบูรณ์
คณะผู้จัดทาหวังเป็นอย่างยิ่งว่า สื่อการสอนชุดนี้จะเป็นประโยชน์ต่อการเรียนการสอน
สาหรับครู และนักเรียนทุกโรงเรียนที่ใช้สื่อชุดนี้ร่วมกับการเรียนการสอนวิชาคณิตศาสตร์ เรื่อง
จานวนจริง นอกจากนี้หากท่านสนใจสื่อการสอนวิชาคณิตศาสตร์ในเรื่องอื่นๆที่คณะผู้จัดทาได้
ดาเนินการไปแล้ว ท่านสามารถดูชื่อเรื่อง และชื่อตอนได้จากรายชื่อสื่อการสอนวิชาคณิตศาสตร์
ทั้งหมดในตอนท้ายของคู่มือฉบับนี้

4. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
3
เรื่อง จานวนจริง(อสมการ)
หมวด เนื้อหา
ตอนที่ 5 (5/9)
หัวข้อย่อย 1. เส้นจานวนและช่วง
2. อสมการที่เกี่ยวข้องกับพหุนามดีกรีหนึ่ง
3. อสมการที่เกี่ยวข้องกับพหุนามดีกรีสูง
จุดประสงค์การเรียนรู้
เพื่อให้ผู้เรียน
1. เข้าใจความหมายของช่วงและเขียนกราฟแทนช่วงได้
2. สามารถแก้อสมการที่เกี่ยวข้องกับพหุนามดีกรีหนึ่งได้
3. สามารถแก้อสมการที่เกี่ยวข้องกับพหุนามดีกรีสูงได้
ผลการเรียนรู้ที่คาดหวัง
ผู้เรียนสามารถ
1. อธิบายความหมายของช่วง และสามารถเขียนกราฟแทนช่วงได้
2. บอกขั้นตอนหลักการในการแก้อสมการที่เกี่ยวข้องกับพหุนามดีกรีหนึ่งได้
3. แก้อสมการที่เกี่ยวข้องกับพหุนามดีกรีหนึ่งได้
4. บอกขั้นตอนหลักการในการแก้อสมการที่เกี่ยวข้องกับพหุนามดีกรีสูงได้
5. แก้อสมการที่เกี่ยวข้องกับพหุนามดีกรีสูงได้

5. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
4
เนื้อหาในสื่อการสอน
เนื้อหาทั้งหมด

6. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
5
1. เส้นจานวนและช่วง

7. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
6
1. เส้นจานวนและช่วง
ในสื่อช่วงแรกนี้ เราจะให้ผู้เรียนได้รู้จักกับ “ช่วง” และการดาเนินการเกี่ยวกับช่วง
ผู้สอนควรย้าให้นักเรียนตระหนักว่า ช่วงคือเซตประเภทหนึ่ง

8. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
7
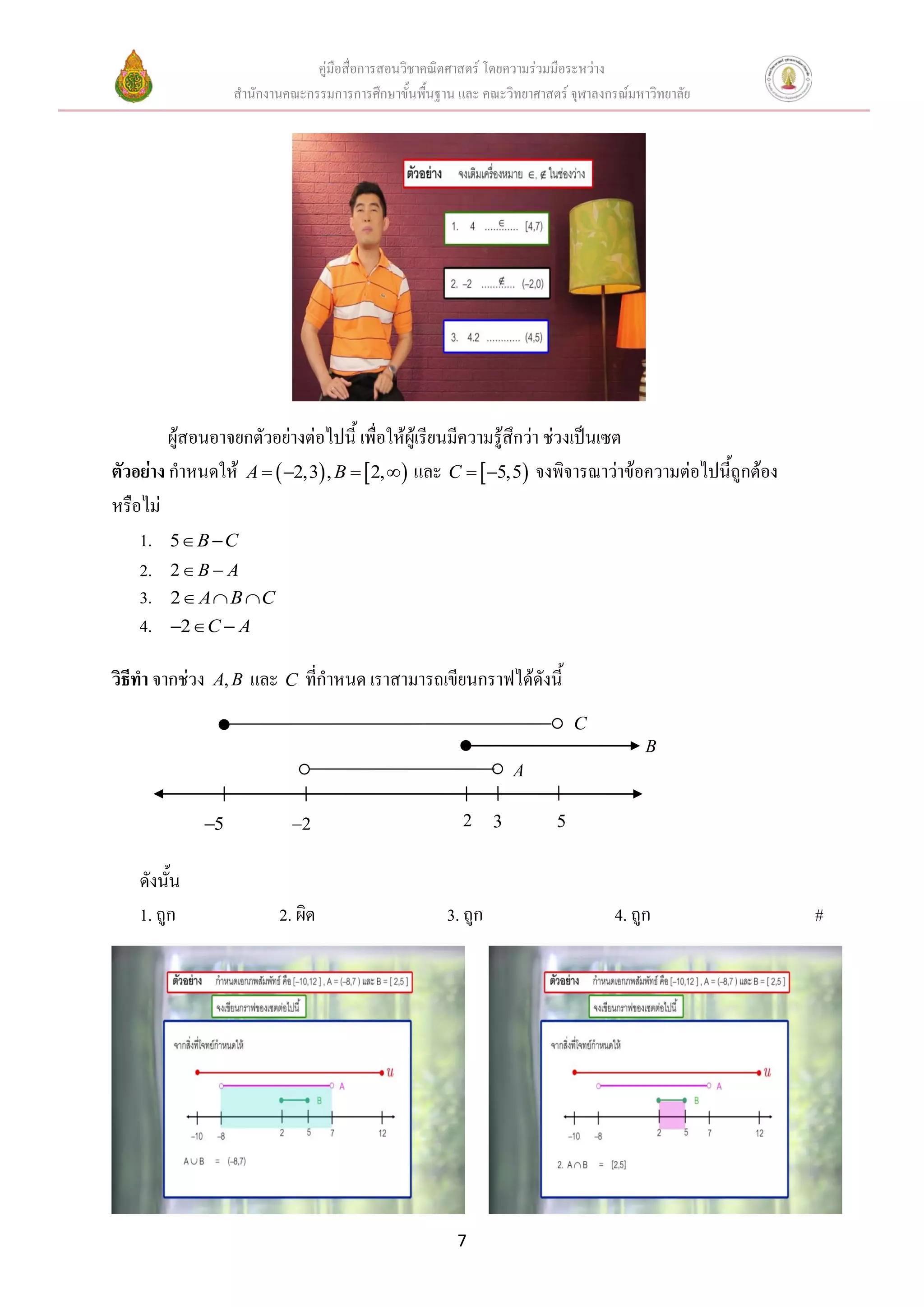
ผู้สอนอาจยกตัวอย่างต่อไปนี้ เพื่อให้ผู้เรียนมีความรู้สึกว่า ช่วงเป็นเซต
ตัวอย่าง กาหนดให้    2,3 , 2,A B    และ  5,5C   จงพิจารณาว่าข้อความต่อไปนี้ถูกต้อง
หรือไม่
1. 5 B C 
2. 2 B A 
3. 2 A B C  
4. 2 C A  
วิธีทา จากช่วง ,A B และ C ที่กาหนด เราสามารถเขียนกราฟได้ดังนี้
ดังนั้น
1. ถูก 2. ผิด 3. ถูก 4. ถูก #
322 55
C
A
B

9. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
8
ตัวอย่าง กาหนดให้      2,10 , 3, , 2,5A B C      และ  10,20D   จงเขียนกราฟของเซต
ต่อไปนี้
1. D A
2.  D B C 
3.  B D A 
วิธีทา จากช่วง , ,A B C และ D ที่โจทย์กาหนด จะได้กราฟดังต่อไปนี้
ดังนั้น
1. D A มีกราฟคือ
2.  D B C  มีกราฟคือ
3 20
2 10 2010
523
B
10 2010
A
C
D
2

10. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
9
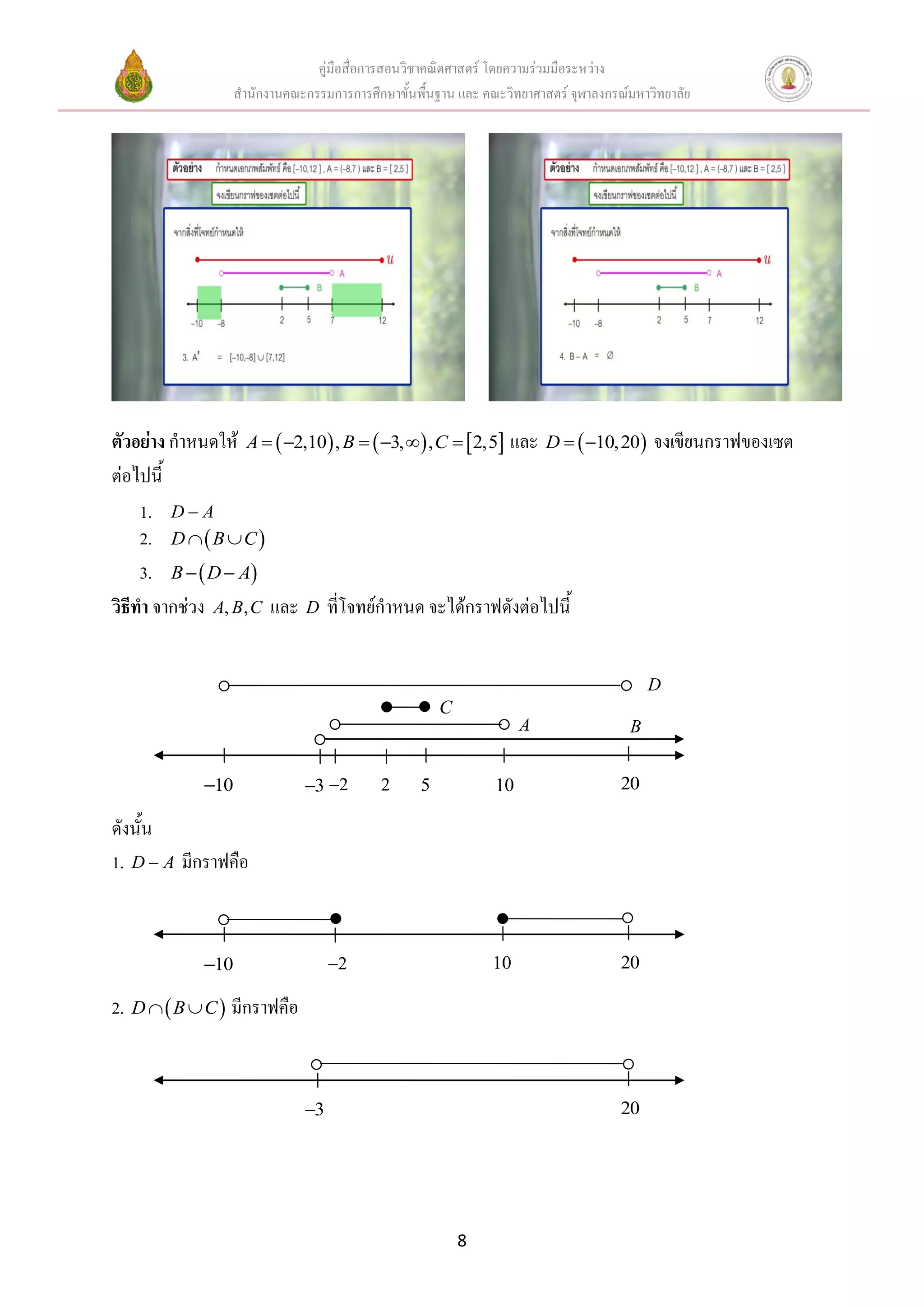
3.  B D A  มีกราฟคือ
#
แบบฝึกหัดเพิ่มเติม
เรื่องเส้นจานวนและช่วง
กาหนดให้    2,5 , 3,8A B  และ  10,4C   จงเขียนกราฟแทนเซตต่อไปนี้
1. A B
2. A B
3.  A B 
4.  A B C 
5. A
กาหนดให้      8,5 , 3,5 , 10,1A B C      ข้อความต่อไปนี้ถูกหรือผิด
6.  1,1 A B C   
7. 5 B C 
8.  A B C 
9. B A  
10.  A B C   
2 10 20

11. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
10
2. อสมการที่เกี่ยวข้องกับพหุนามดีกรีหนึ่ง

12. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
11
2. อสมการที่เกี่ยวข้องกับพหุนามดีกรีหนึ่ง
เพื่อให้ผู้เรียนมีความคล่องตัวในการประยุกต์สมบัติของจานวนจริงในการแก้อสมการ ผู้สอนควรให้
ผู้เรียนลองทาแบบฝึกหัดในตัวอย่างต่อไปนี้
ตัวอย่าง ให้ , , ,a b c d  จงพิจารณาว่าข้อความต่อไปนี้ถูกหรือผิด
1. ถ้า 0 a c  และ 0 b d  จะได้ ab cd
2. ถ้า a b แล้ว 3 3
a b
3. ถ้า 0a c  และ 0b d  จะได้ 0ab cd 
4. ถ้า 0bd  และ ,a c b d  จะได้ a c
d b

5. ถ้า a c และ b d จะได้ ab cd
6. ถ้า a c และ b d จะได้ 2 2 2 2
a b c d
7. ถ้า a c และ b d จะได้ a c
b d

8. ถ้า 0 a c  และ 0 b d  จะได้ 0 1
ab
cd
 
9. ถ้า a b แล้ว 2 2
a b
10. ถ้า 0 1a  แล้ว 2
0 a a 
11. ถ้า a b แล้ว a b
12. ถ้า 2 2
a b แล้ว a b
เฉลย
1. ถูก 2. ถูก 3. ถูก 4. ผิด 5. ผิด
6. ผิด 7. ผิด 8. ถูก 9. ผิด 10. ถูก
11. ถูก 12. ผิด

13. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
12
ถ้า a b และ 0c  แล้ว ac bc
ถ้า a b และ 0c  แล้ว ac bc
ตัวอย่างต่อไปนี้ เป็นตัวอย่างที่จะฝึกให้ผู้เรียนระวังเรื่องการคูณอสมการ ตามสมบัติต่อไปนี้
ตัวอย่าง จงแก้สมการต่อไปนี้
1. 3 9x 
2. 4 0
2
x
  
วิธีทา
1. จาก 3 9x  เรานา 1
3
 คูณตลอดจะได้ว่า
   
1 1
3 9
3 3
x   
3x  
2. จาก 4 0
2
x
  
4
2
x
  
นา 2 คูณตลอด
8x  #
ข้อสังเกต จากตัวอย่างข้างต้น เรานาค่าคงตัวที่เป็นจานวนลบคูณตลอด เครื่องหมายของอสมการต้อง
เปลี่ยนไป

14. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
13
ตัวอย่าง จงแก้อสมการต่อไปนี้ และแสดงคาตอบโดยใช้เส้นจานวน
1. 2 5x x 
2. 3 2x x 
วิธีทา
1. 2 5x x 
5 0x  
5x  
2. 3 2x x 
3 x
#
5
3

15. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
14
แบบฝึกหัดเพิ่มเติม
เรื่องอสมการที่เกี่ยวข้องกับพหุนามดีกรีหนึ่ง
1-5 จงหาเซตคาตอบของอสมการต่อไปนี้
1. 2 5x 
2. 9 3x x 
3. 5
3
x
x  
4. 3 18 0x  
5. 3 1
4
3
x 

6-10 จงแก้อสมการต่อไปนี้ และแสดงคาตอบโดยเส้นจานวน
6. 4 2 8 3x x  
7. 3 2 2 8x x  
8. 5 4 12x  
9. 5 5 3 2 2 1x x x    
10. 8 2
3
2 3
x x
x
 
 

16. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
15
3. อสมการที่เกี่ยวข้องกับพหุนามดีกรีสูง

17. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
16
3. อสมการที่เกี่ยวข้องกับพหุนามดีกรีสูง
ในหัวข้อนี้ผู้เรียนจะได้เรียนรู้วิธีแก้สมการพหุนามที่มีดีกรีมากกว่าหนึ่ง

18. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
17

19. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
18
0 0
ผู้สอนอาจยกตัวอย่างต่อไปนี้เพิ่มเติม
ตัวอย่าง ให้  2
| 3 5 2 0A x x x     และ 2 1
| 0
3
x
B x
x
 
   
 
จงหา A B
วิธีทา
หา A 2
3 5 2 0x x  
  3 2 1 0x x  
ดังนั้น 2
( ,1)
3
A 
หา B
2 1
0
3
x
x



  2 1 3 0x x   โดยที่ 3x 
12
3
  

20. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
19
3 1
3
0
ดังนั้น  
1
( , ] 3,
2
B     
หา A B
จากกราฟจะได้ว่า A B   #
ตัวอย่าง จงแก้อสมการ 2 2
8 3 3 2 2x x x    
วิธีทา 2 2
8 3 3 2 2x x x     ก็ต่อเมื่อ
2
8 3 3x x   และ 2 2
3 3 2 2x x  
กรณี 1 2
8 3 3x x  
2
3 8 3 0x x  
  3 1 3 0x x  
1
3
x  หรือ 3x  
กรณี 2 2 2
3 3 2 2x x  
2
5 0x  
  5 5 0x x  
5 5x  
312
3
1
2

A
B
31
2

  

21. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
20
2 1 3
 +  000
5 5
5 53
1
3
ดังนั้น ค่า x ที่สอดคล้องทั้ง 2 กรณีคือ 1
( , 5)
3
ตัวอย่าง จงแก้สมการ 3
7 6 0x x   และแสดงคาตอบโดยเส้นจานวน
วิธีทา
แยกตัวประกอบ 3
7 6x x  โดยทฤษฎีบทแยกตัวประกอบ
ให้   3
7 6p x x x   จะได้ว่า  1 1 7 6 0p      
ดังนั้น 1x  เป็นตัวประกอบหนึ่งของ 3
7 6x x 
เพราะว่า
ดังนั้น       3 2
7 6 1 6 1 3 2x x x x x x x x         
2
3
3 2
2
2
6
1 7 6
7 6
6 6
6 6
x x
x x x
x x
x x
x x
x
x
 
  

  
 
 
 

22. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
21
2 1 3
2 1 1 2
+ + + 0 0 00
ดังนั้น ค่า x ที่ทาให้ 3
7 6 0x x   คือ
   2, 1 3,x     ซึ่งแสดงโดยเส้นจานวนได้ดังนี้
#
ตัวอย่าง จงแก้อสมการ 4 2
5 4 0x x  
วิธีทา
4 2
5 4 0x x  
  2 2
4 1 0x x  
    2 2 1 1 0x x x x    
ดังนั้น ค่า x ที่สอดคล้องกับอสมการ 4 2
5 4 0x x   คือ    2, 1 1,2x    #
ตัวอย่าง จงหาเซตคาตอบของอสมการ 2
2 3 0x x  
วิธีทา 2
2 3 0x x  
 2
2 1 2 0x x   
 
2
1 2 0x   

23. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
22
เนื่องจากทุกจานวนจริง x นั้น  
2
1 0x   เสมอ
ดังนั้นเซตคาตอบของอสมการคือ #
ตัวอย่าง จงหาเซตคาตอบของอสมการ 2
2 3 0x x  
วิธีทา เนื่องจากทุกจานวนจริง x นั้น  
22
2 3 1 2 0x x x      เสมอ
ดังนั้น จึงไม่มีจานวนจริง x ที่ทาให้ 2
2 3 0x x  
ทาให้เซตคาตอบของอสมการ 2
2 3 0x x   คือ  #
แบบฝึกหัดเพิ่มเติม
เรื่อง สมการที่เกี่ยวข้องกับพหุนามดีกรีสูง
1-10 จงแก้อสมการต่อไปนี้
1.   2 1 0x x  
2.   2 1 5 0x x  
3.    1 3 2 0x x x   
4.   4
1 5 0x x  
5.     3
2 1 1 0x x x   
6. 2
2 3 0x x  
7. 2
2 10 5 27x x x  
8. 2 2 2
3 5 2 4x x x x x    
9. 4
1x 
10. 3 2
6 4x x x  

24. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
23
4. สรุปสาระสาคัญประจาตอน

25. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
24
4. สรุปสาระสาคัญประจาตอน
สาระสาคัญในสื่อตอนนี้ คือการศึกษาเรื่อง ช่วง และการแก้อสมการพหุนามที่เกี่ยวข้องกับพหุนาม

26. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
25
ภาคผนวกที่ 1
แบบฝึกหัด/เนื้อหาเพิ่มเติม

27. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
26
1
3
 1
แบบฝึกหัดระคน
1. ข้อใดเป็นเซตคาตอบของอสมการ 3 1 8 2 5x x x    
1.  2. 7
( , )
2
 3.  13, 4.  
7
( , ) 13,
2
  
2. เซตคาตอบของอสมการ 1 2 4
6 3 3
x x 
  เป็นสับเซตของข้อใด
1.  ,20 2.  20,  3.  100,100 4.    ,20 20,40 
3. ให้  2 1
| 3 4 0 , | 2
2
x
A x x x B x
x
 
        
 
และ คือเซตของจานวนเต็ม แล้ว
ข้อใดถูกต้อง
1. A B    2. A B 3. A B  4. A B 
4. ให้  2
| 3 6 8 0A x x x     จงพิจารณาข้อความต่อไปนี้
ก.  2
| 2 1A x x x    ข.  2
| 2 3A x x x A    
1. ก ถูก ข ถูก 2. ก ผิด ข ถูก
3. ก ถูก ข ผิด 4. ก ผิด ข ผิด
5. ให้      1,5 , 2,3 , 1,5A B C    ข้อใดต่อไปนี้ถูกต้อง
ก.  A B C B A    ข. A B B C  
1. ก ถูก ข ถูก 2. ก ผิด ข ถูก
3. ก ถูก ข ผิด 4. ก ผิด ข ผิด
6. ให้    | 3 1 2 10A x x x    และ  2
| 4 0B x x   แล้ว A B คือเซตในข้อใด
1.  2,3 2.  2,3 3.  0,8 4.  2,
7. เซตคาตอบของอสมการ 3 1
2
1
x
x



เป็นสับเซตของข้อใด
1.  2
| 1 0x x   2.  | 1 1x x   3.    , 1 1,10   4. 1
| 0
1
x
x
x
 
 
 
8. ให้  2
| 2 5 10 25A x x x x    จงพิจารณาว่าข้อความต่อไปนี้ ข้อใดถูกต้อง
ก.    0, 5,A    ข.  3,5A 
1. ก ถูก ข ถูก 2. ก ผิด ข ถูก
3. ก ถูก ข ผิด 4. ก ผิด ข ผิด
9. กาหนดให้ 3 1
| 0
x
A x
x
 
  
 
และ  2
| 2 3 1 0B x x x     แล้ว A B คือข้อใด
1.

28. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
27
1
3
 1
1
2
1
1
2
1
2.
3.
4.
10. ให้ A เป็นเซตคาตอบของอสมการ 2
2 4 6 0x x   และ  2
| 2 4 5 0B x x x     แล้ว
ข้อใดต่อไปนี้ถูกต้อง
1.  2 14, 2 14A B      2.  0,A B  
3.  0,A B   4. B A

29. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
28
ภาคผนวกที่ 2
เฉลยแบบฝึกหัด

30. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
29
53
32
82
52
52
เฉลยแบบฝึกหัดเพิ่มเติม
เรื่องเส้นจานวนและช่วง
1.
2.
3.
4.
5.
6. ถูก 7. ถูก 8. ถูก 9. ผิด 10. ผิด
เฉลยแบบฝึกหัดเพิ่มเติม
เรื่องอสมการที่เกี่ยวข้องกับพหุนามดีกรีหนึ่ง
1. 5
{ }
2
x x  2. 9
{ }
2
x x   3. 15
{ }
4
x x  
4. { 6}x x  5. 11
{ }
3
x x  

31. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
30
6
10
1 8
3
8
5

6.
7.
8.
9.
10.
เฉลยแบบฝึกหัดเพิ่มเติม
เรื่องอสมการที่เกี่ยวข้องกับพหุนามดีกรีสูง
1. 2 1x    2. 1
2
x  หรือ 5x  
3. 2x   หรือ 1 3x   4. 1x   หรือ 5x 
5. 1 1x   หรือ 2x  6. x
7. 9
2
x  หรือ 3x  8. 2
0
3
x  
9. 1x  หรือ 1x   10. 3x   หรือ 2 1x  

32. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
31
เฉลยแบบฝึกหัดระคน
1. 1 2. 2 3. 1 4. 1 5. 2
6. 1 7. 1 8. 4 9. 3 10. 4

33. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
32
รายชื่อสื่อการสอนวิชาคณิตศาสตร์
จานวน 92 ตอน

34. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
33
รายชื่อสื่อการสอนวิชาคณิตศาสตร์ จานวน 92 ตอน
เรื่อง ตอน
เซต บทนา เรื่อง เซต
ความหมายของเซต
เซตกาลังและการดาเนินการบนเซต
เอกลักษณ์ของการดาเนินการบนเซตและแผนภาพเวนน์-ออยเลอร์
สื่อปฏิสัมพันธ์เรื่องแผนภาพเวนน์-ออยเลอร์
การให้เหตุผลและตรรกศาสตร์ บทนา เรื่อง การให้เหตุผลและตรรกศาสตร์
การให้เหตุผล
ประพจน์และการสมมูล
สัจนิรันดร์และการอ้างเหตุผล
ประโยคเปิดและวลีบ่งปริมาณ
สื่อปฏิสัมพันธ์เรื่องหอคอยฮานอย
สื่อปฏิสัมพันธ์เรื่องตารางค่าความจริง
จานวนจริง บทนา เรื่อง จานวนจริง
สมบัติของจานวนจริง
การแยกตัวประกอบ
ทฤษฏีบทตัวประกอบ
สมการพหุนาม
อสมการ
เทคนิคการแก้อสมการ
ค่าสัมบูรณ์
การแก้อสมการค่าสัมบูรณ์
กราฟค่าสัมบูรณ์
สื่อปฏิสัมพันธ์เรื่องช่วงบนเส้นจานวน
สื่อปฏิสัมพันธ์เรื่องสมการและอสมการพหุนาม
สื่อปฏิสัมพันธ์เรื่องกราฟค่าสัมบูรณ์
ทฤษฎีจานวนเบื้องต้น บทนา เรื่อง ทฤษฎีจานวนเบื้องต้น
การหารลงตัวและจานวนเฉพาะ
(การหารลงตัวและตัวหารร่วมมาก)ตัวหารร่วมมากและตัวคูณร่วมน้อย
ความสัมพันธ์และฟังก์ชัน บทนา เรื่อง ความสัมพันธ์และฟังก์ชัน
ความสัมพันธ์

35. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
34
เรื่อง ตอน
ความสัมพันธ์และฟังก์ชัน โดเมนและเรนจ์
อินเวอร์สของความสัมพันธ์และบทนิยามของฟังก์ชัน
ฟังก์ชันเบื้องต้น
พีชคณิตของฟังก์ชัน
อินเวอร์สของฟังก์ชันและฟังก์ชันอินเวอร์ส
ฟังก์ชันประกอบ
ฟังก์ชันชี้กาลังและฟังก์ชันลอการิทึม บทนา เรื่อง ฟังก์ชันชี้กาลังและฟังก์ชันลอการิทึม
เลขยกกาลัง
ฟังก์ชันชี้กาลังและฟังก์ชันลอการิทึม
ลอการิทึม
อสมการเลขชี้กาลัง
อสมการลอการิทึม
ตรีโกณมิติ บทนา เรื่อง ตรีโกณมิติ
อัตราส่วนตรีโกณมิติ
เอกลักษณ์ของอัตราส่วนตรีโกณมิติ และวงกลมหนึ่งหน่วย
ฟังก์ชันตรีโกณมิติ 1
ฟังก์ชันตรีโกณมิติ 2
ฟังก์ชันตรีโกณมิติ 3
กฎของไซน์และโคไซน์
กราฟของฟังก์ชันตรีโกณมิติ
ฟังก์ชันตรีโกณมิติผกผัน
สื่อปฏิสัมพันธ์เรื่องมุมบนวงกลมหนึ่งหน่วย
สื่อปฏิสัมพันธ์เรื่องกราฟของฟังก์ชันตรีโกณมิติ
สื่อปฏิสัมพันธ์เรื่องกฎของไซน์และกฎของโคไซน์
กาหนดการเชิงเส้น บทนา เรื่อง กาหนดการเชิงเส้น
การสร้างแบบจาลองทางคณิตศาสตร์
การหาค่าสุดขีด
ลาดับและอนุกรม บทนา เรื่อง ลาดับและอนุกรม
ลาดับ
การประยุกต์ลาดับเลขคณิตและเรขาคณิต
ลิมิตของลาดับ
ผลบวกย่อย
อนุกรม
ทฤษฎีบทการลู่เข้าของอนุกรม

36. คู่มือสื่อการสอนวิชาคณิตศาสตร์ โดยความร่วมมือระหว่าง
สานักงานคณะกรรมการการศึกษาขั้นพื้นฐาน และ คณะวิทยาศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
35
เรื่อง ตอน
การนับและความน่าจะเป็น
.
บทนา เรื่อง การนับและความน่าจะเป็น
การนับเบื้องต้น
การเรียงสับเปลี่ยน
การจัดหมู่
ทฤษฎีบททวินาม
การทดลองสุ่ม
ความน่าจะเป็น 1
ความน่าจะเป็น 2
สถิติและการวิเคราะห์ข้อมูล บทนา เรื่อง สถิติและการวิเคราะห์ข้อมูล
บทนา เนื้อหา
แนวโน้มเข้าสู่ส่วนกลาง 1
แนวโน้มเข้าสู่ส่วนกลาง 2
แนวโน้มเข้าสู่ส่วนกลาง 3
การกระจายของข้อมูล
การกระจายสัมบูรณ์ 1
การกระจายสัมบูรณ์ 2
การกระจายสัมบูรณ์ 3
การกระจายสัมพัทธ์
คะแนนมาตรฐาน
ความสัมพันธ์ระหว่างข้อมูล 1
ความสัมพันธ์ระหว่างข้อมูล 2
โปรแกรมการคานวณทางสถิติ 1
โปรแกรมการคานวณทางสถิติ 2
โครงงานคณิตศาสตร์ การลงทุน SET50 โดยวิธีการลงทุนแบบถัวเฉลี่ย
ปัญหาการวางตัวเบี้ยบนตารางจัตุรัส
การถอดรากที่สาม
เส้นตรงล้อมเส้นโค้ง
กระเบื้องที่ยืดหดได้