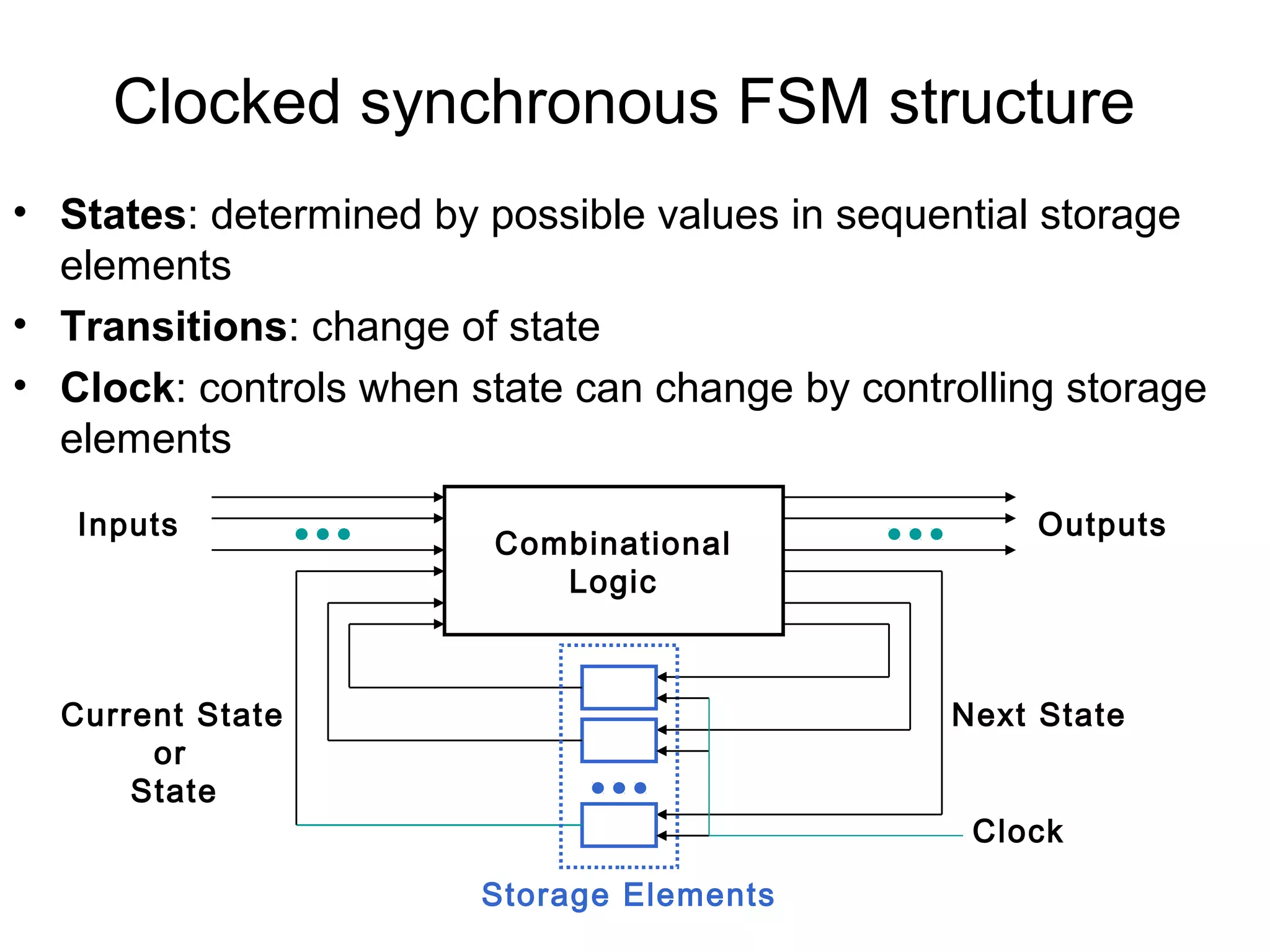
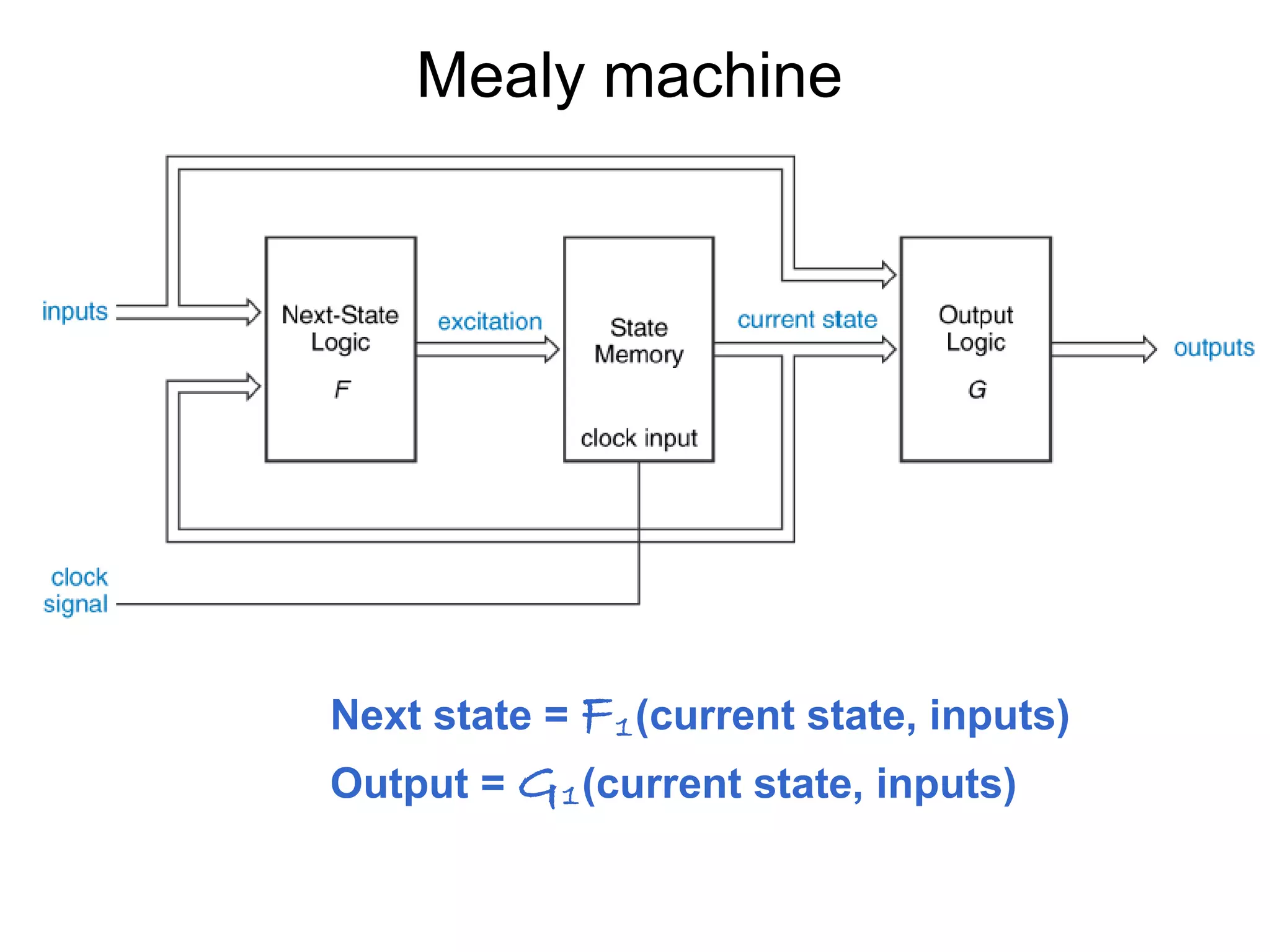
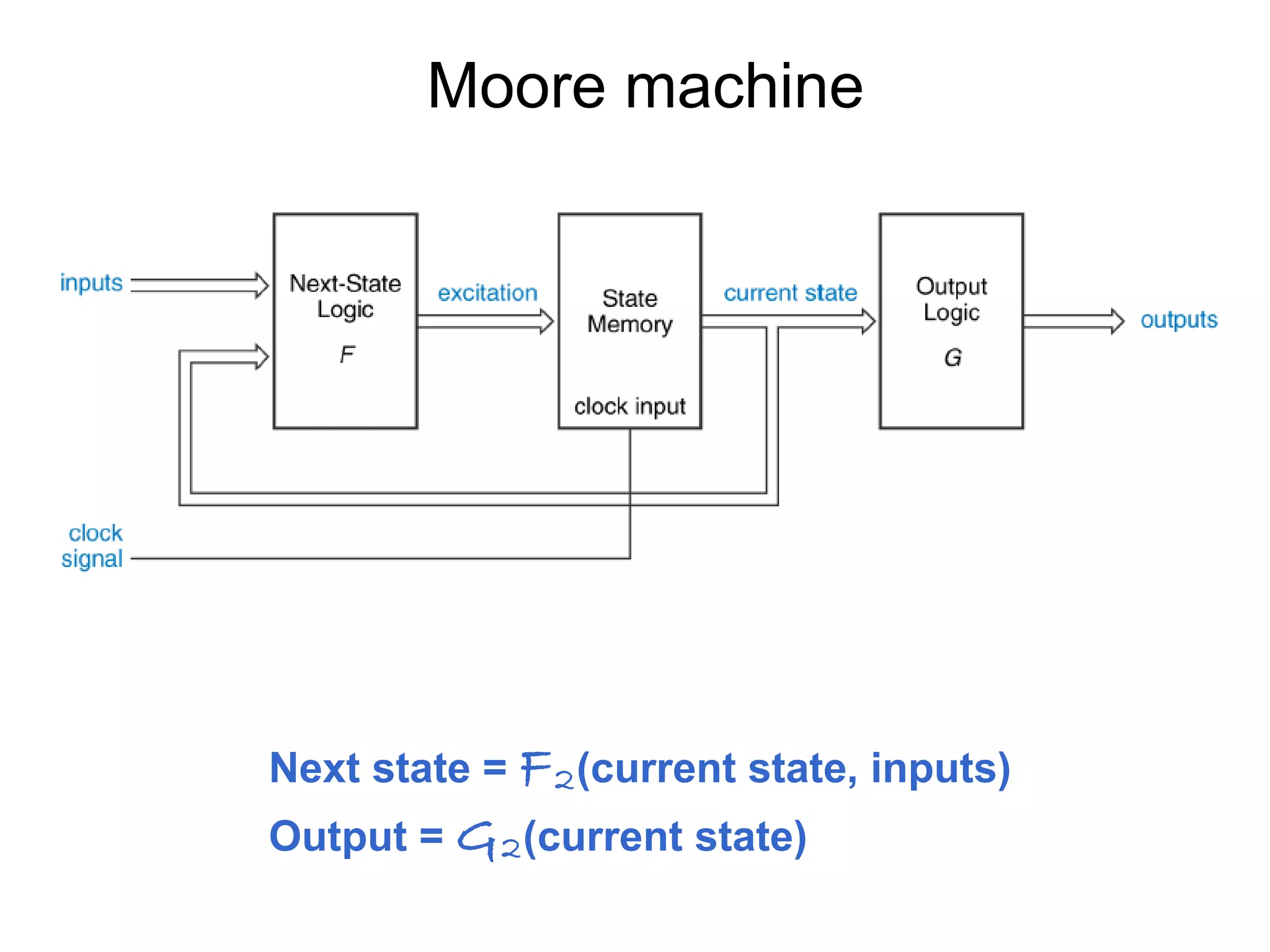
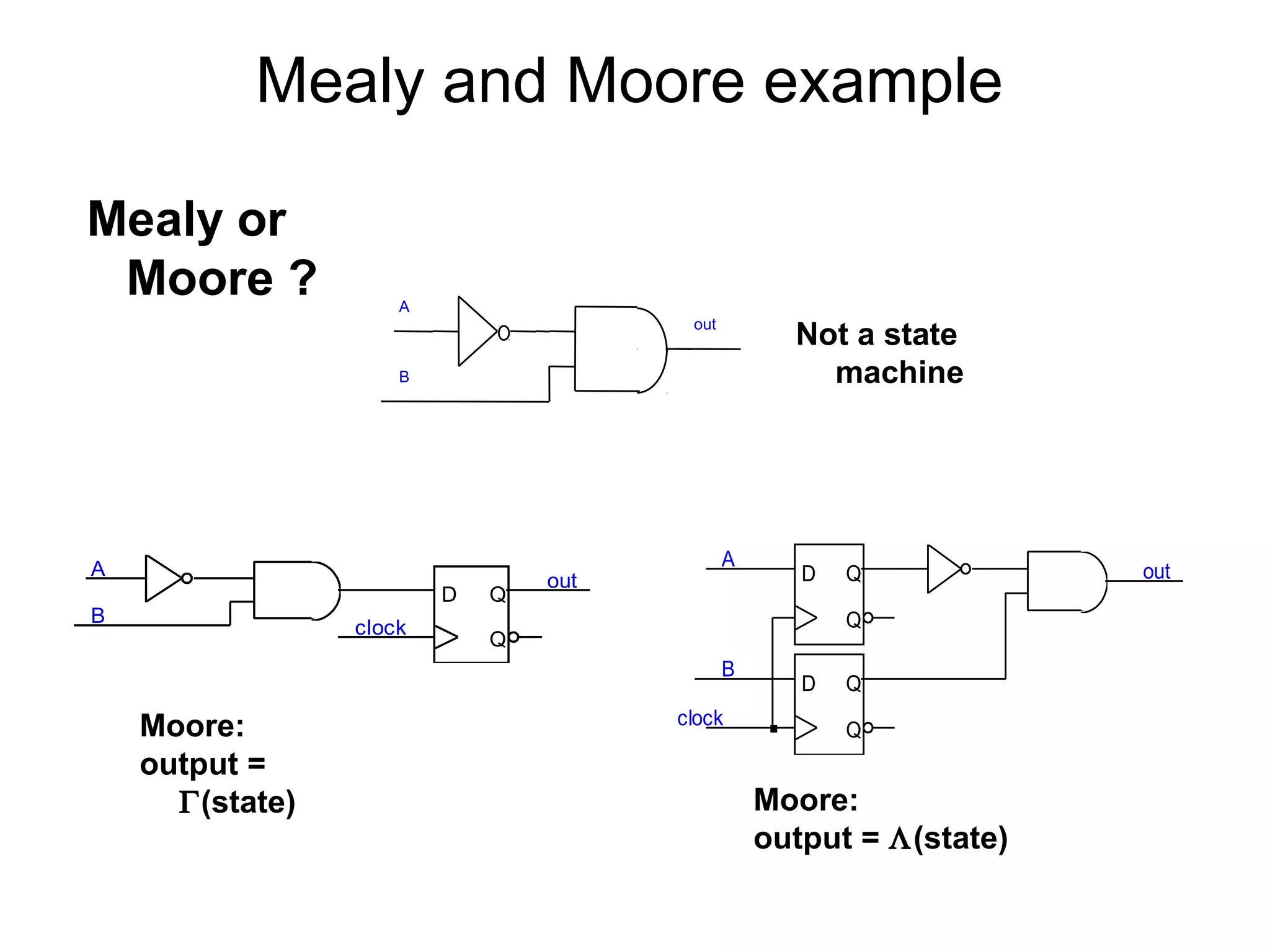
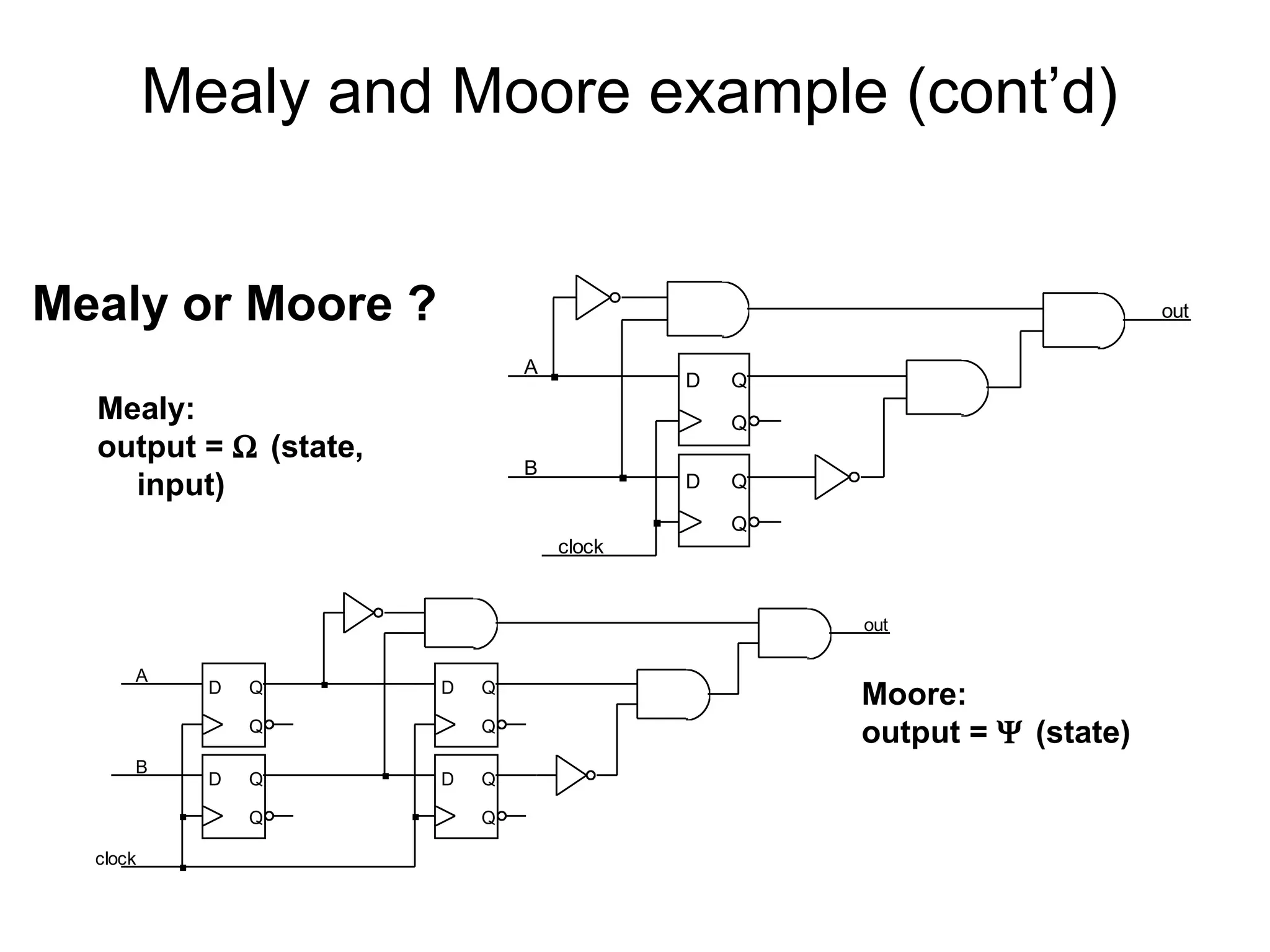
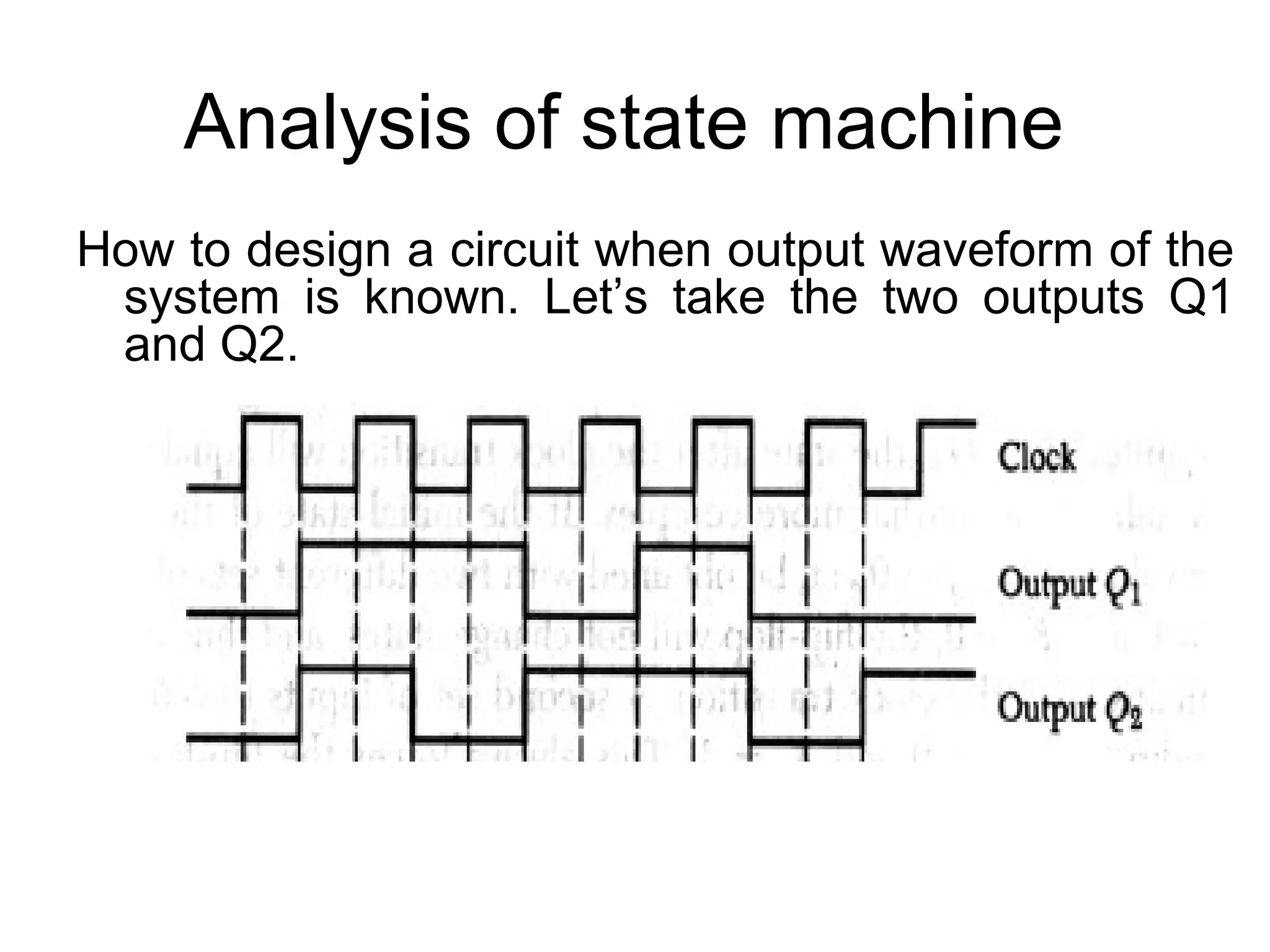
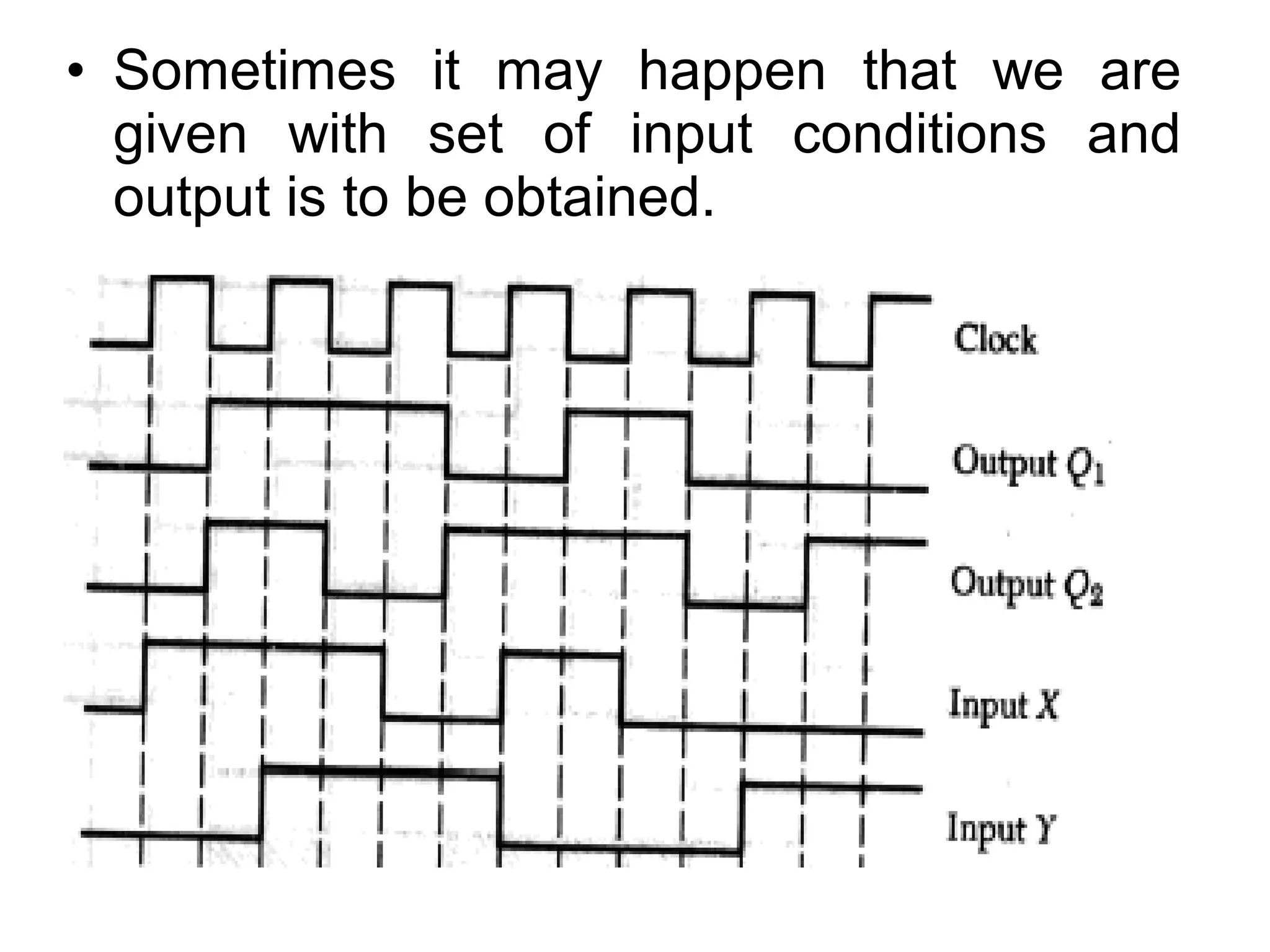
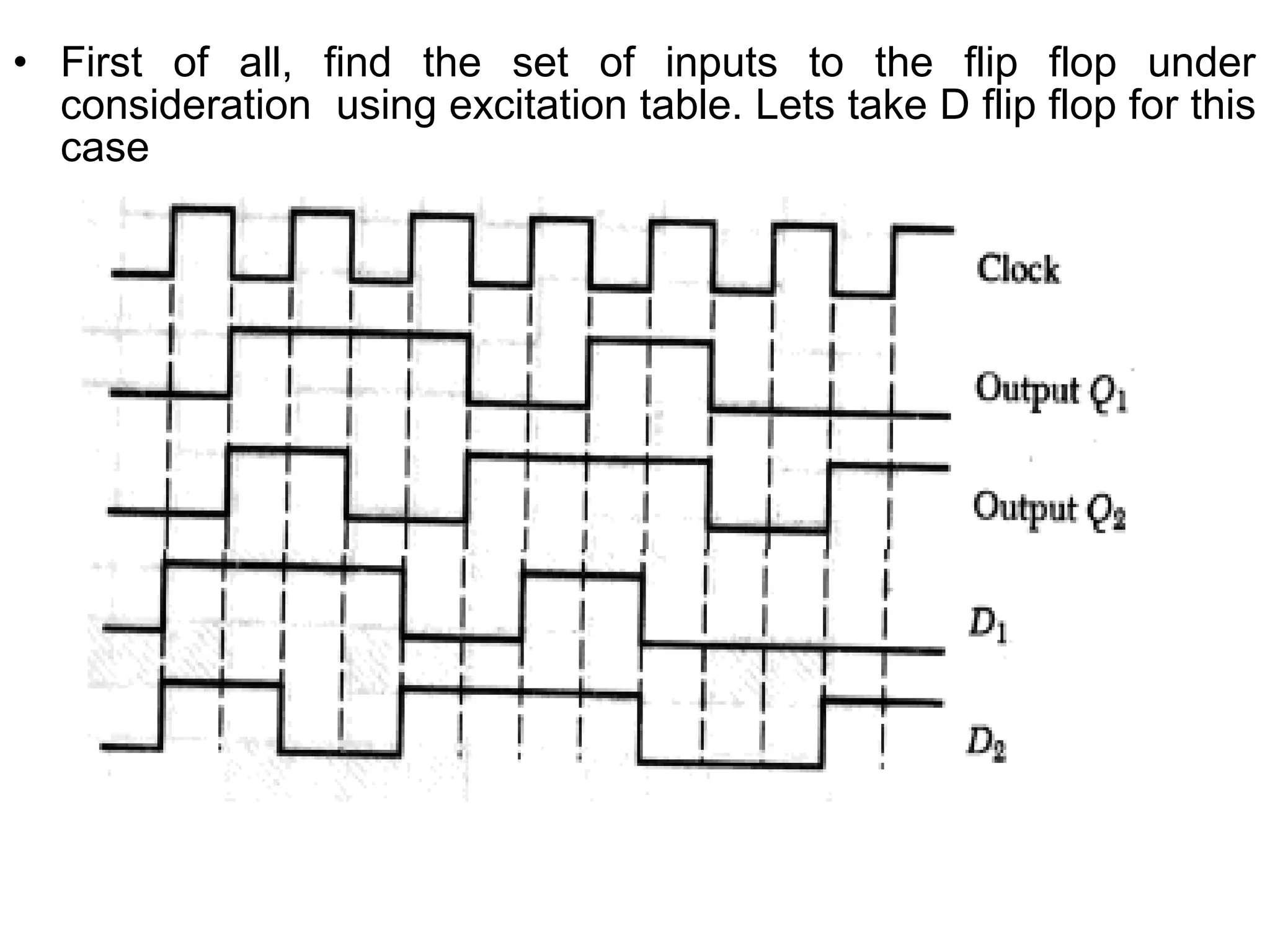
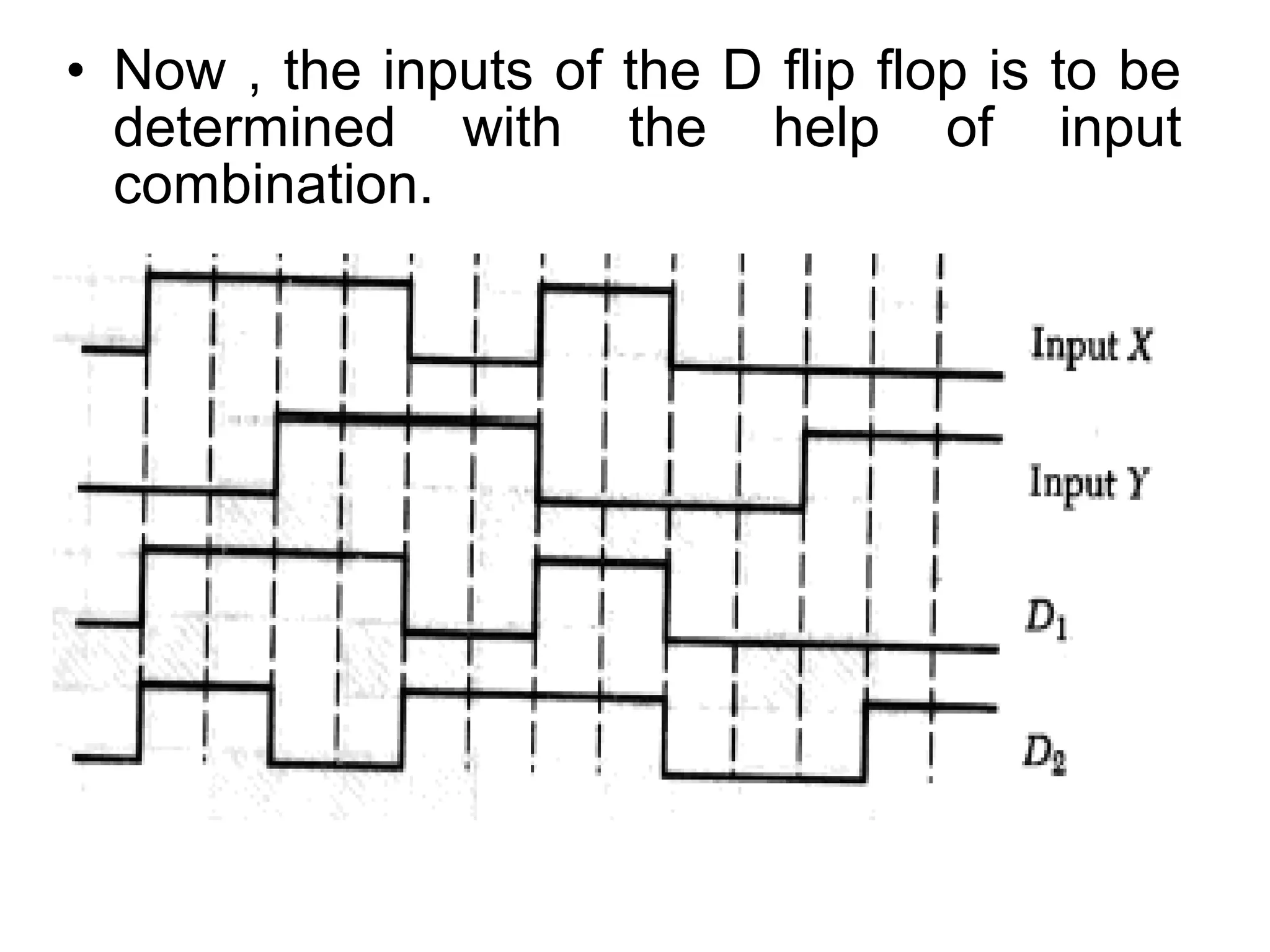
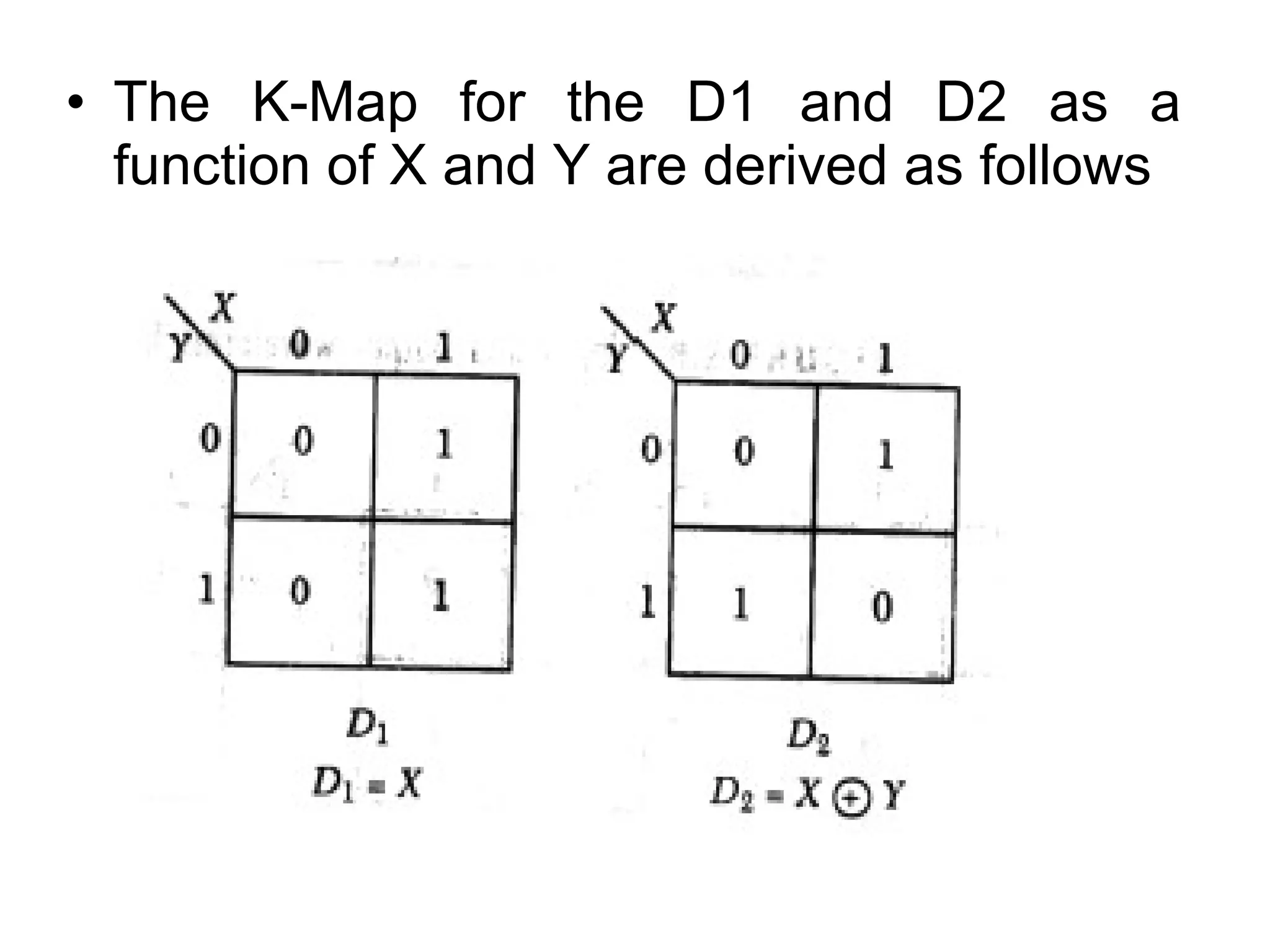
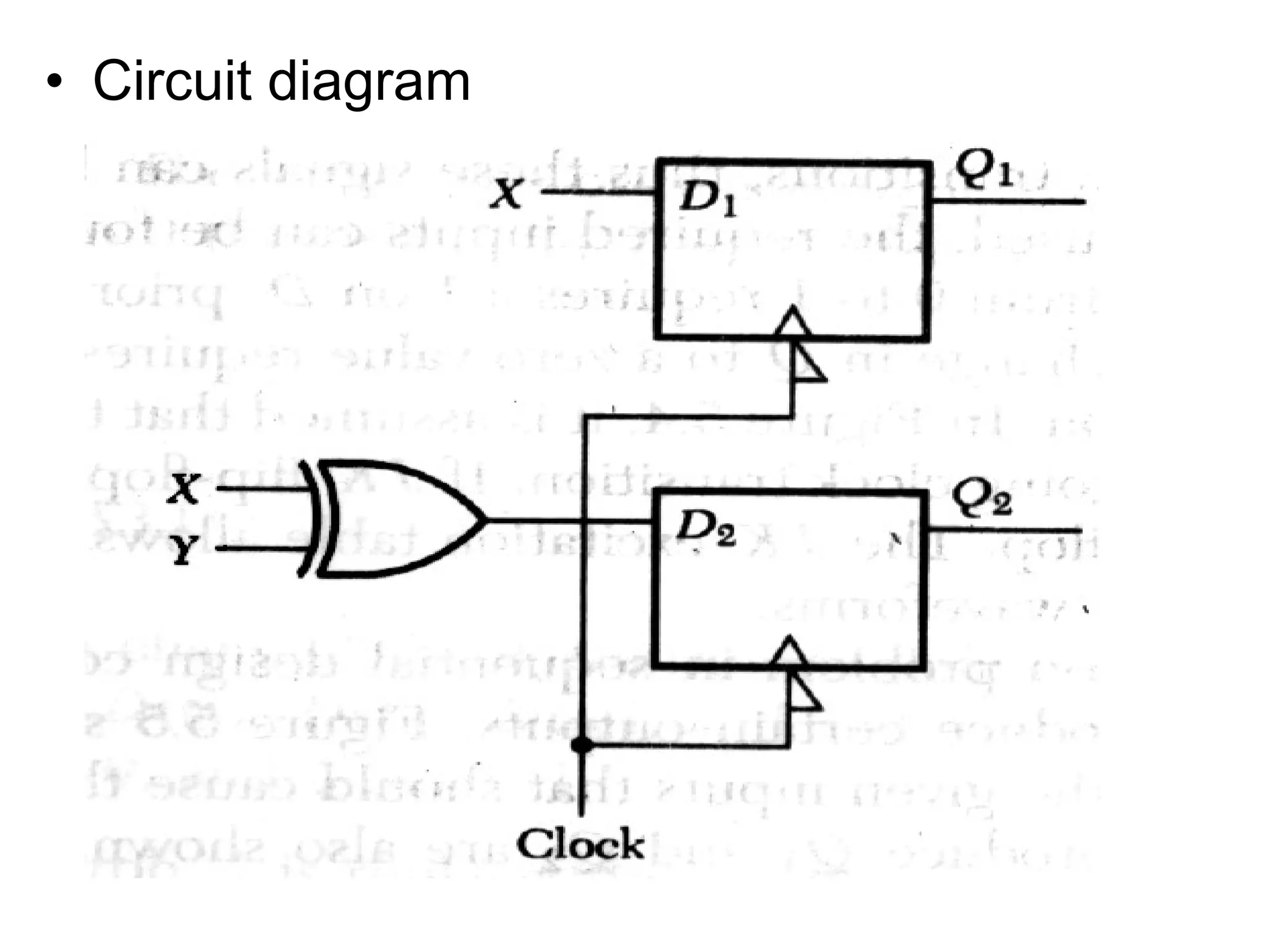
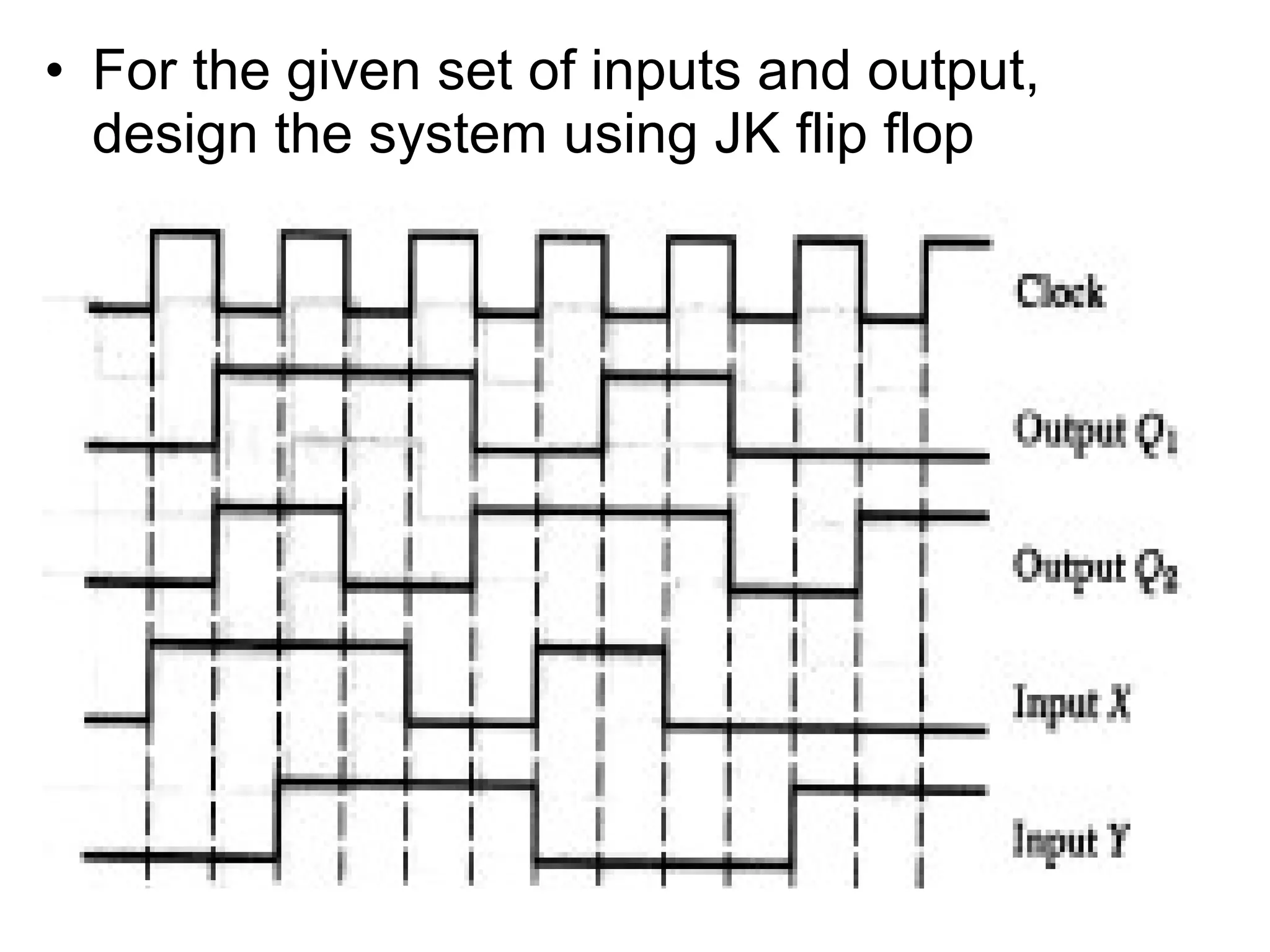
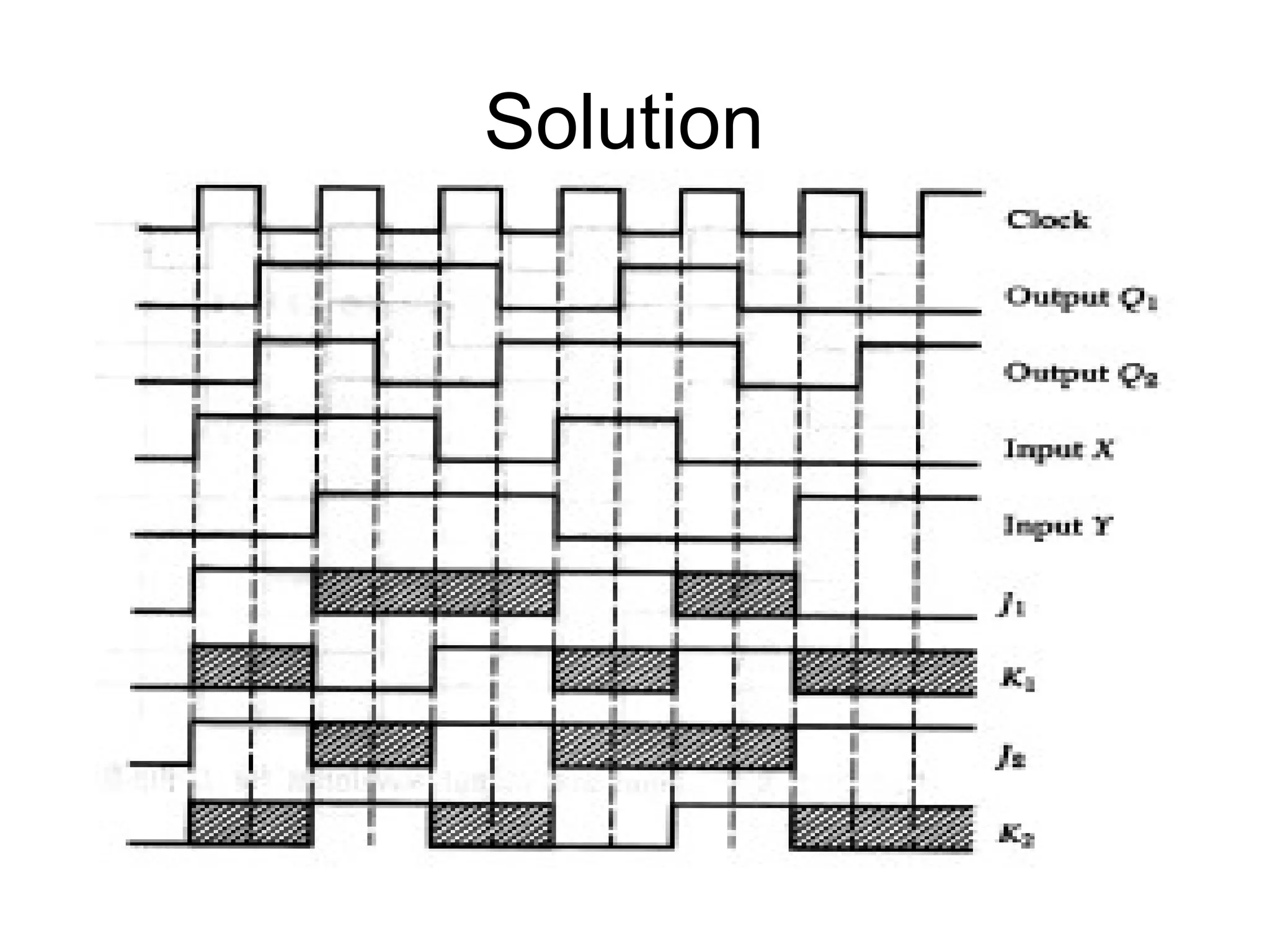
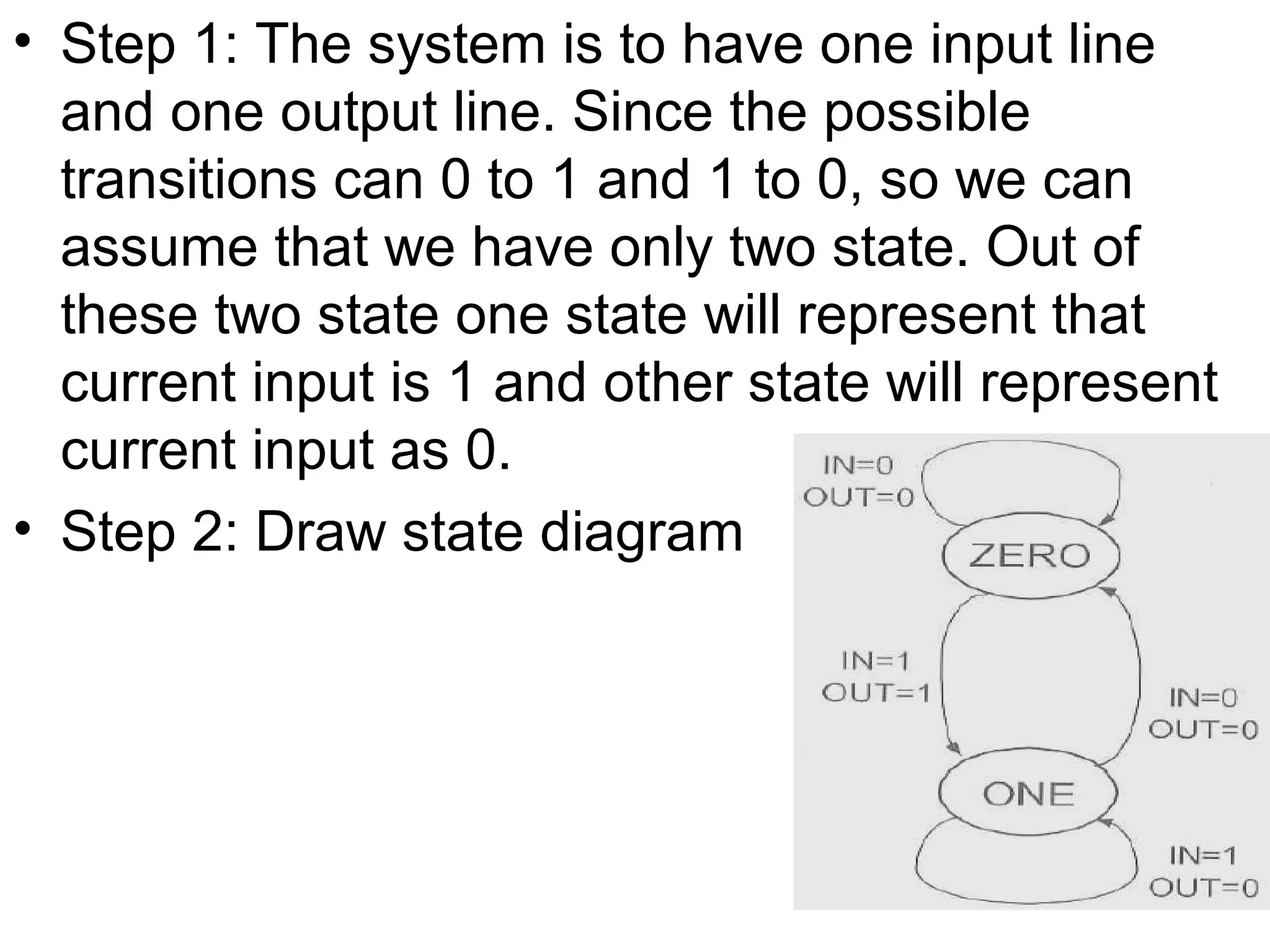
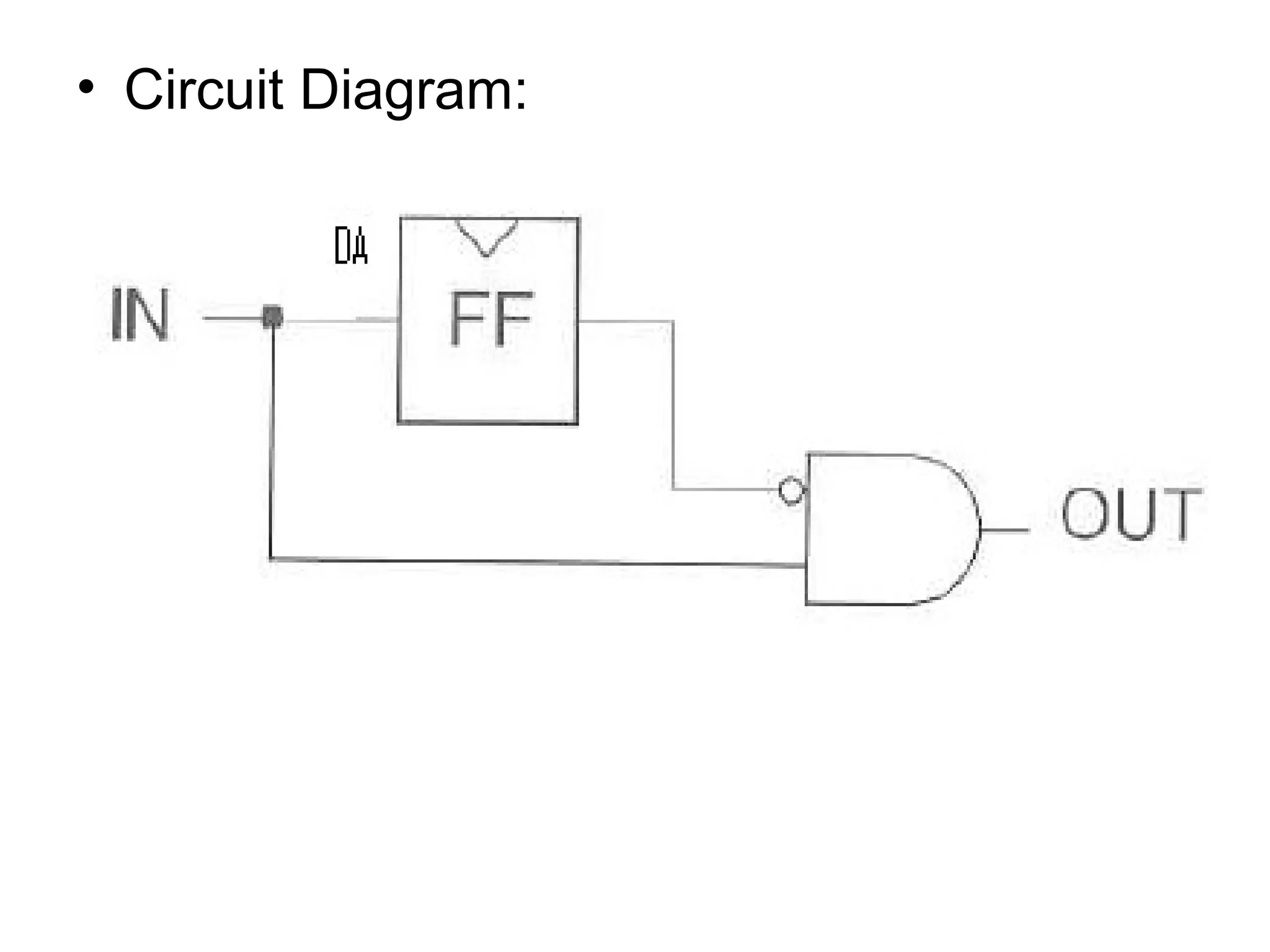
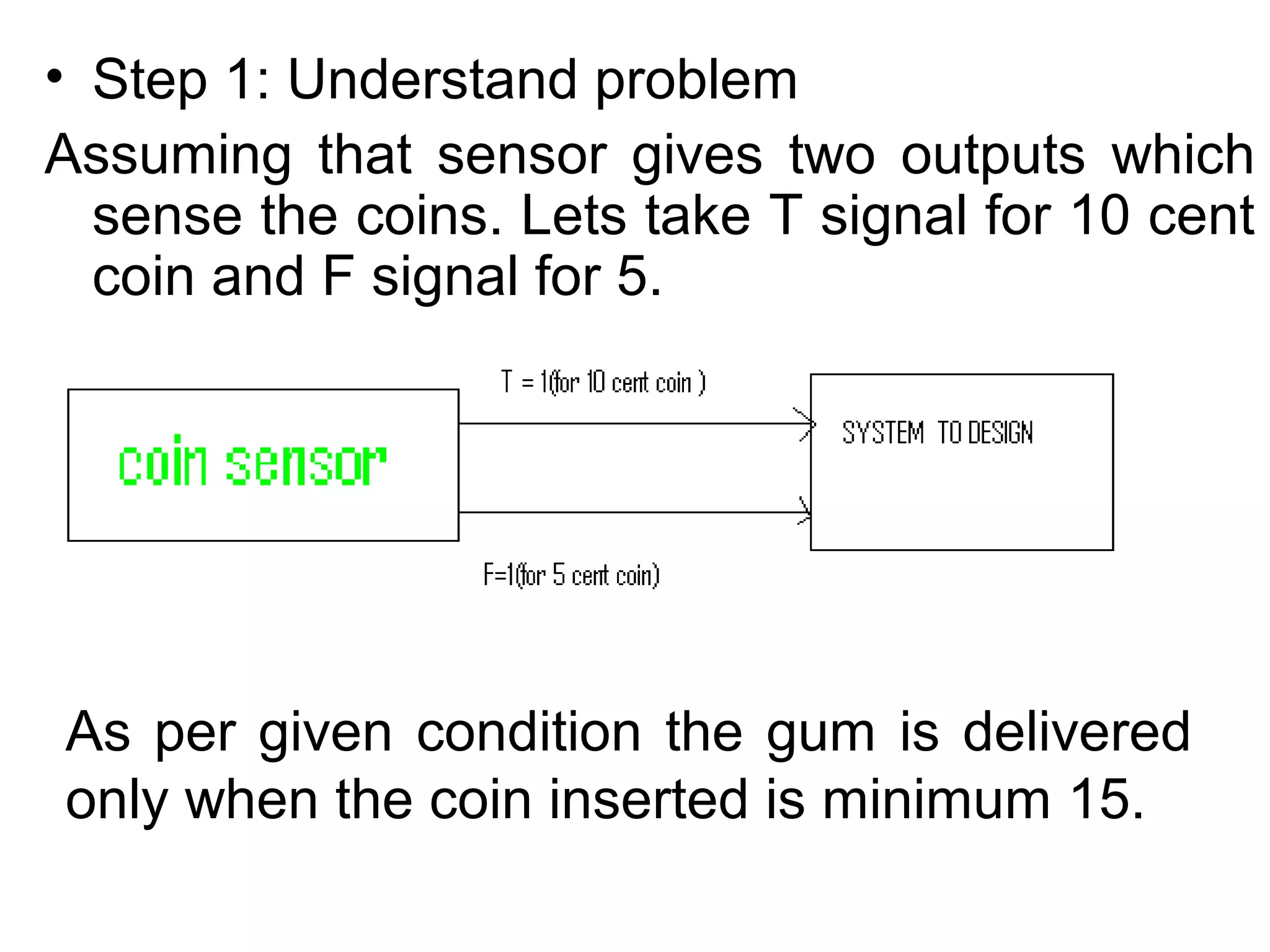
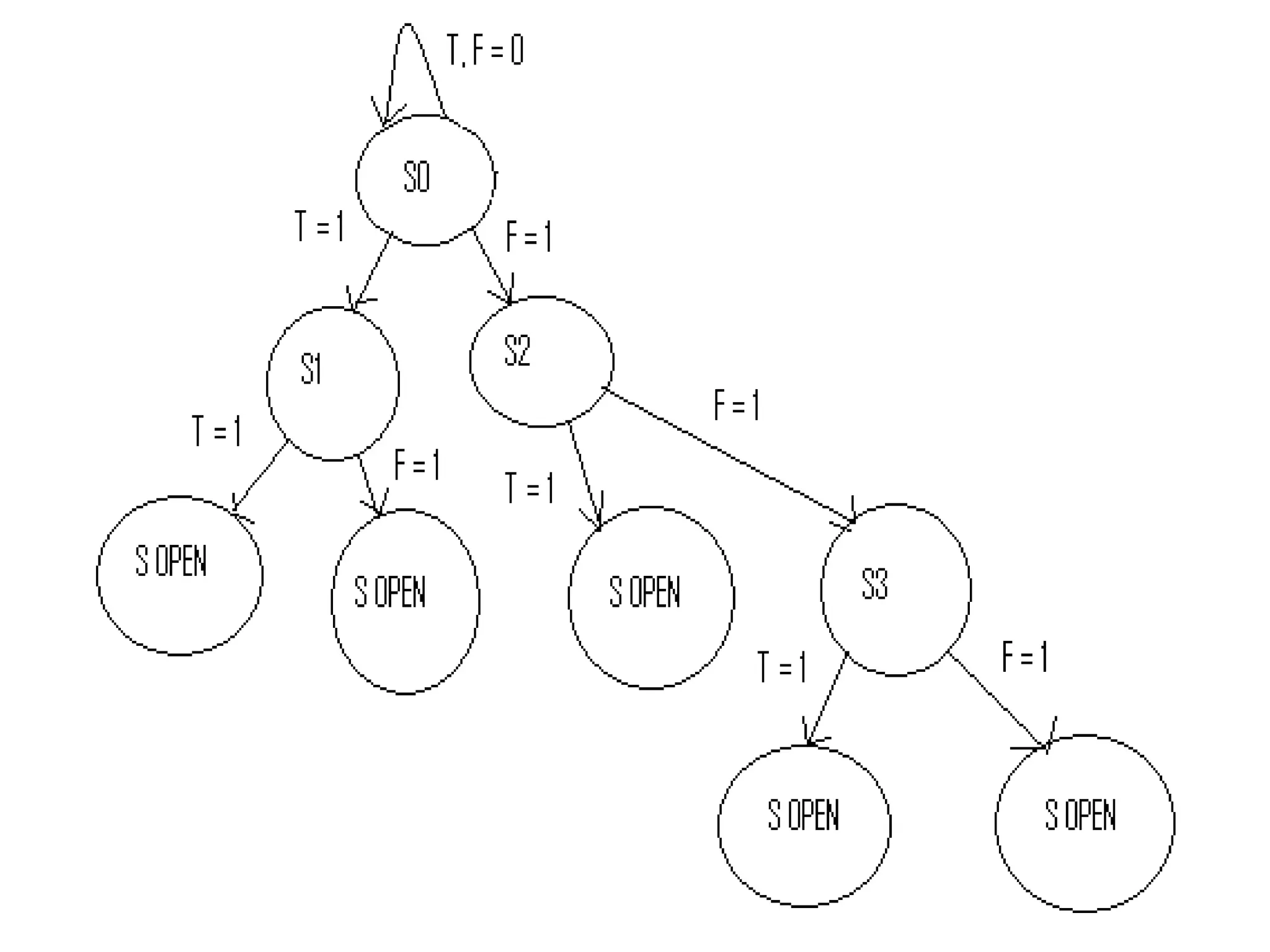
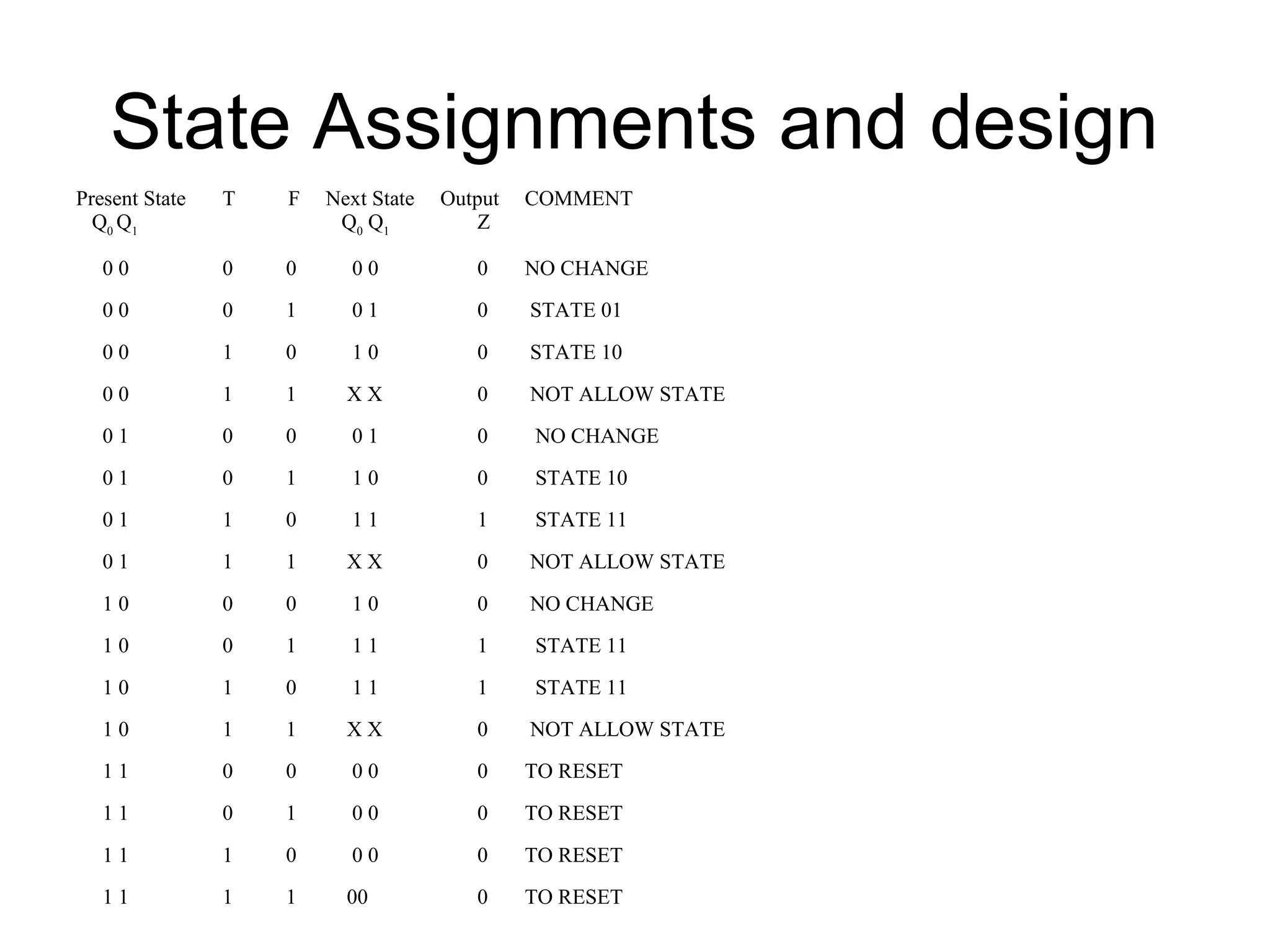
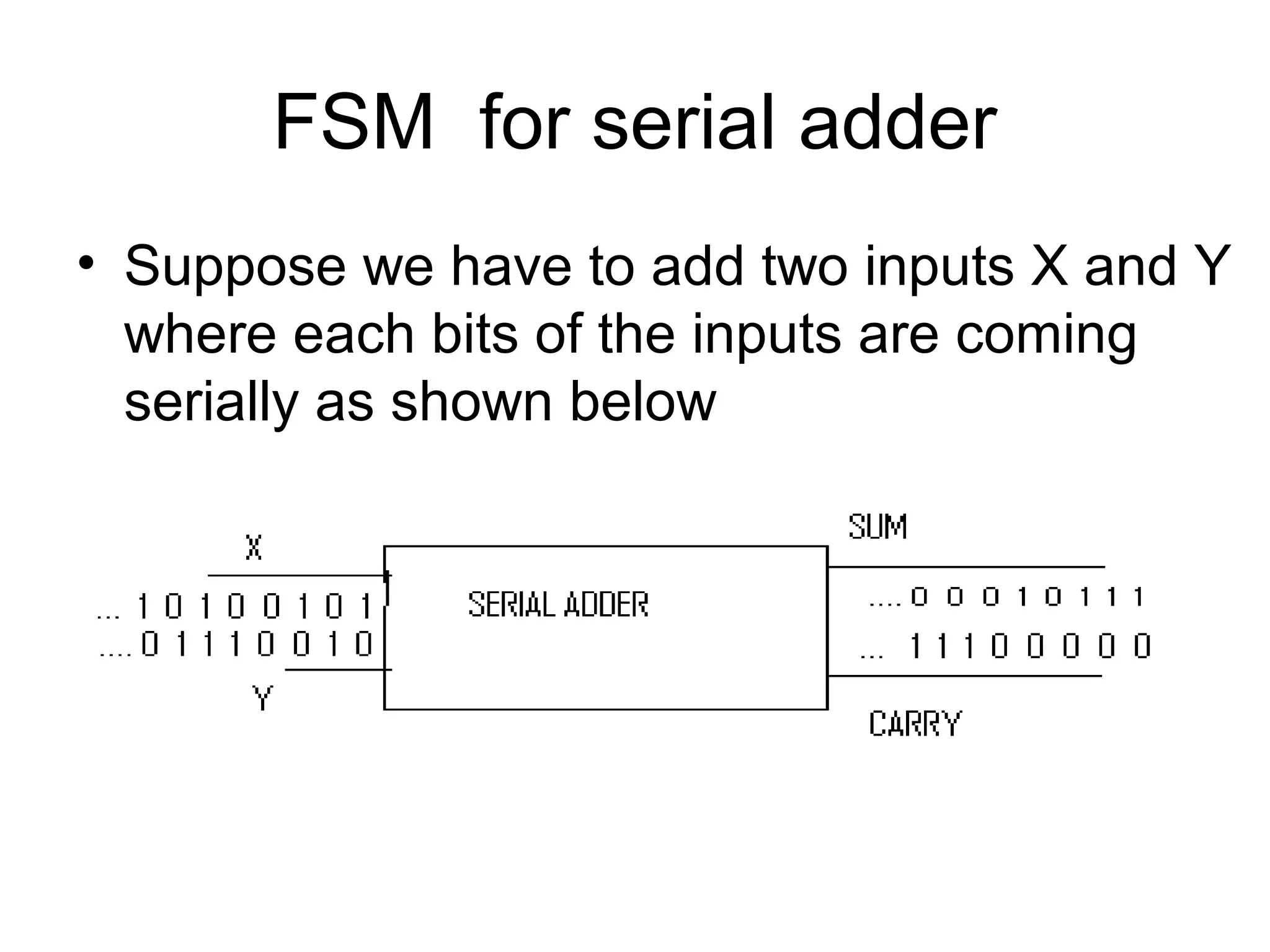
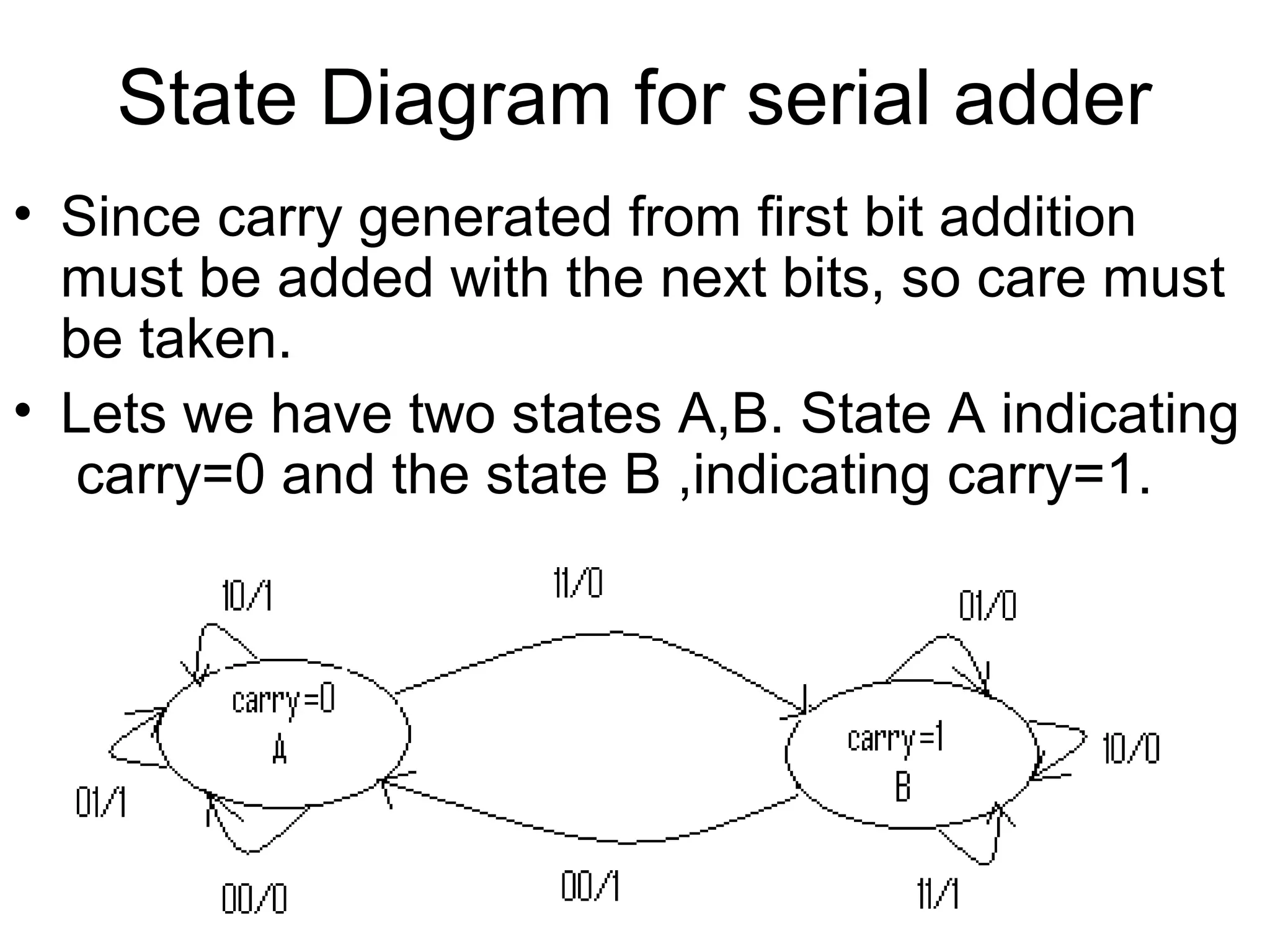
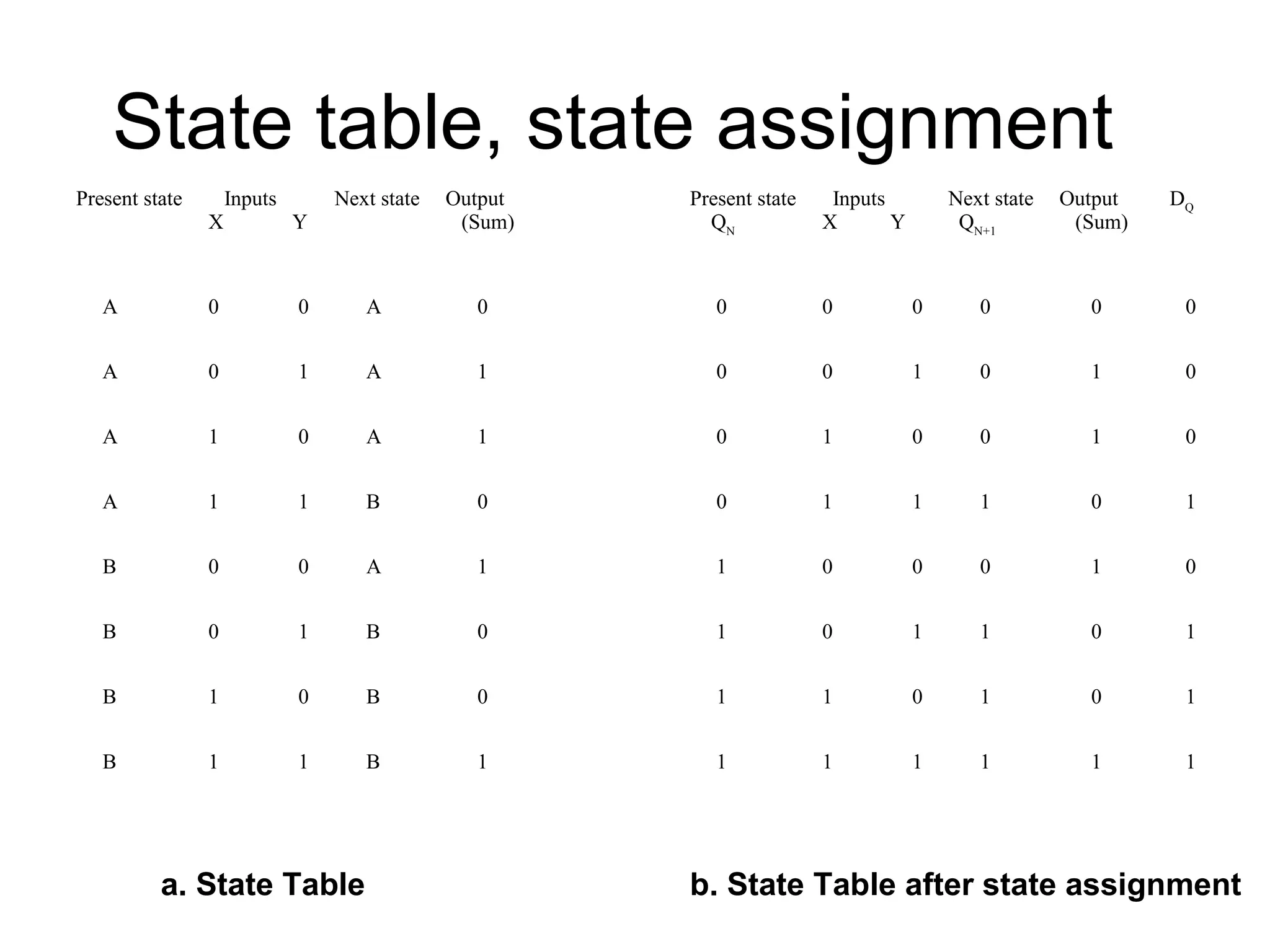
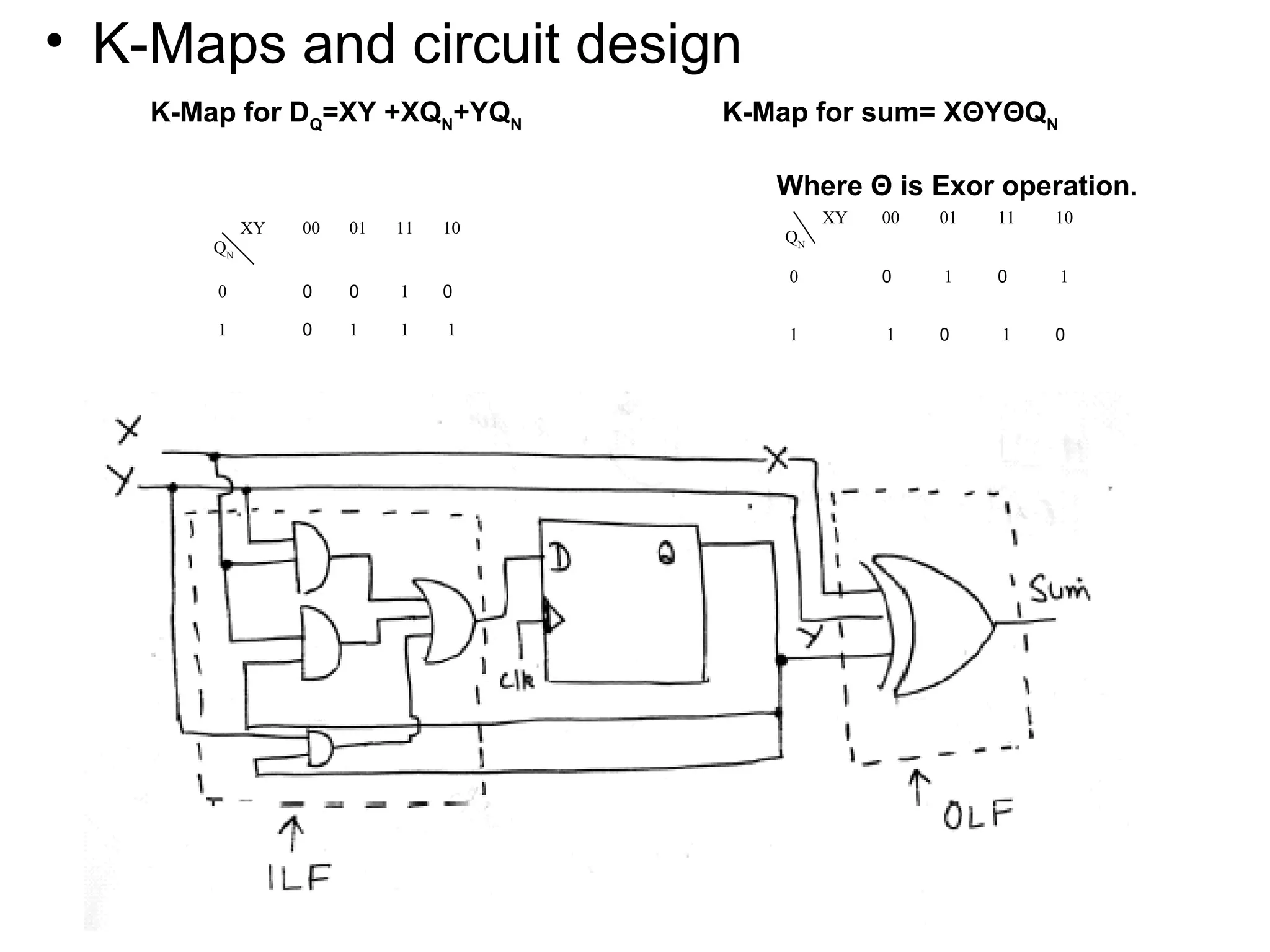
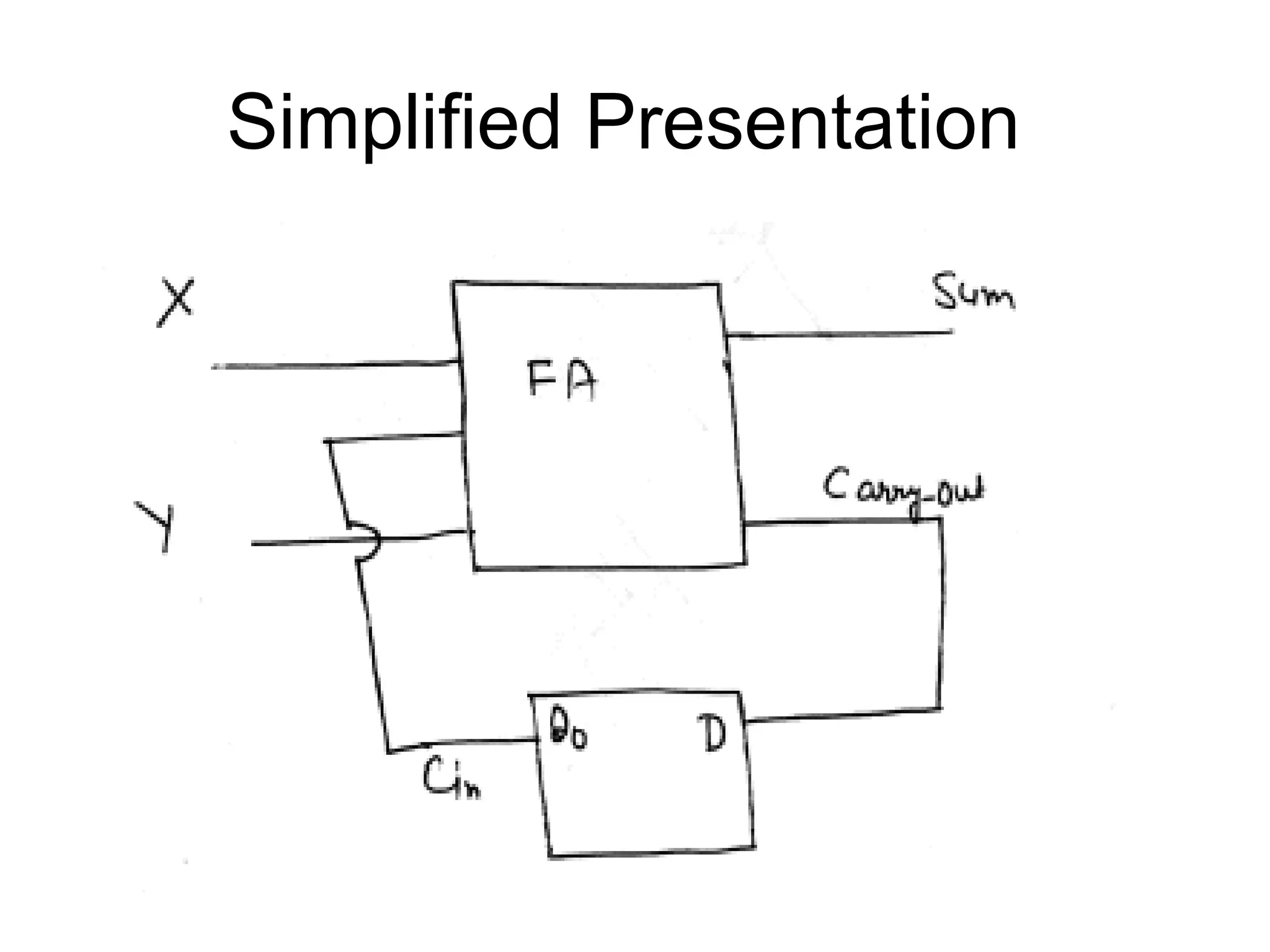
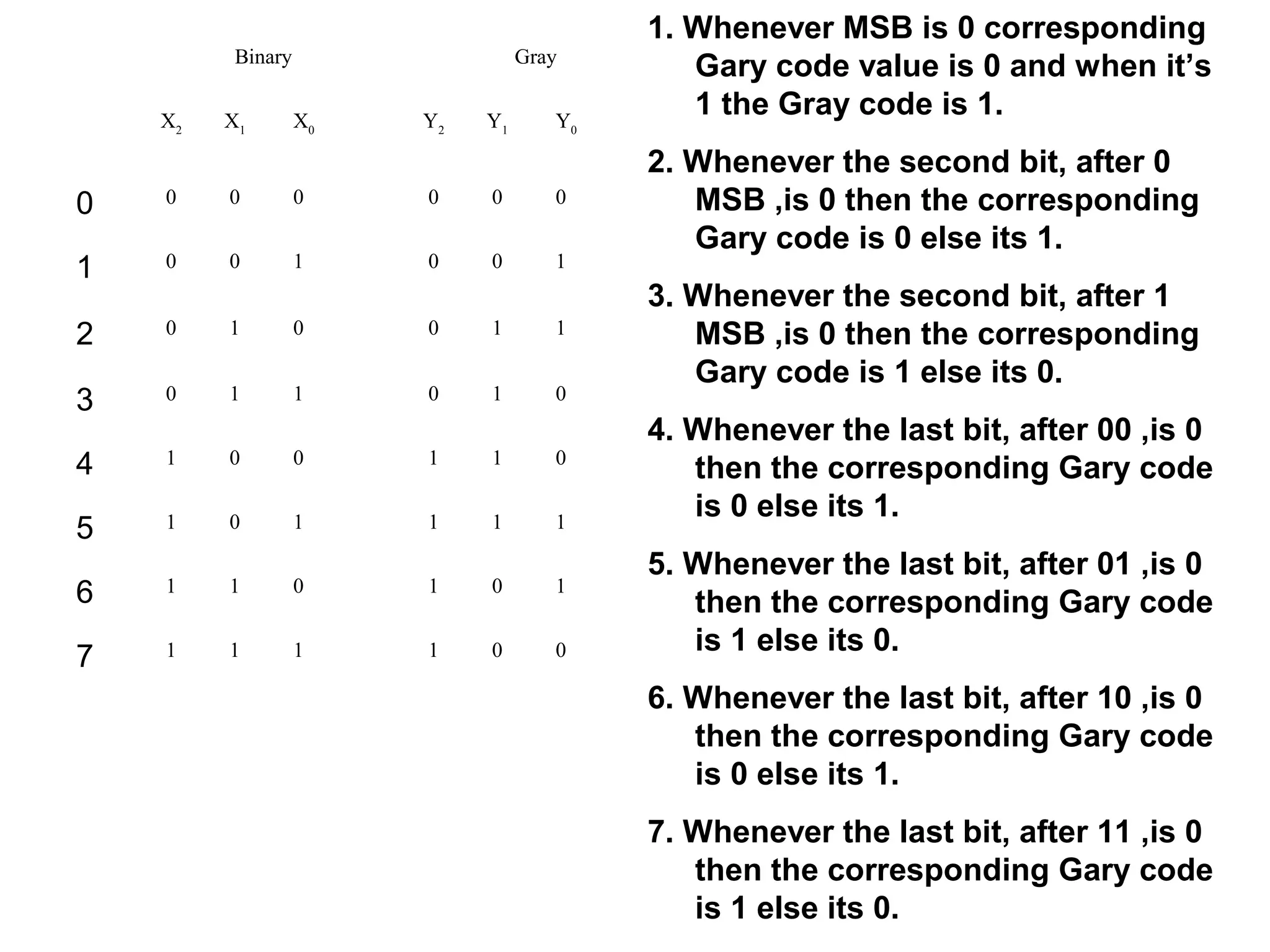
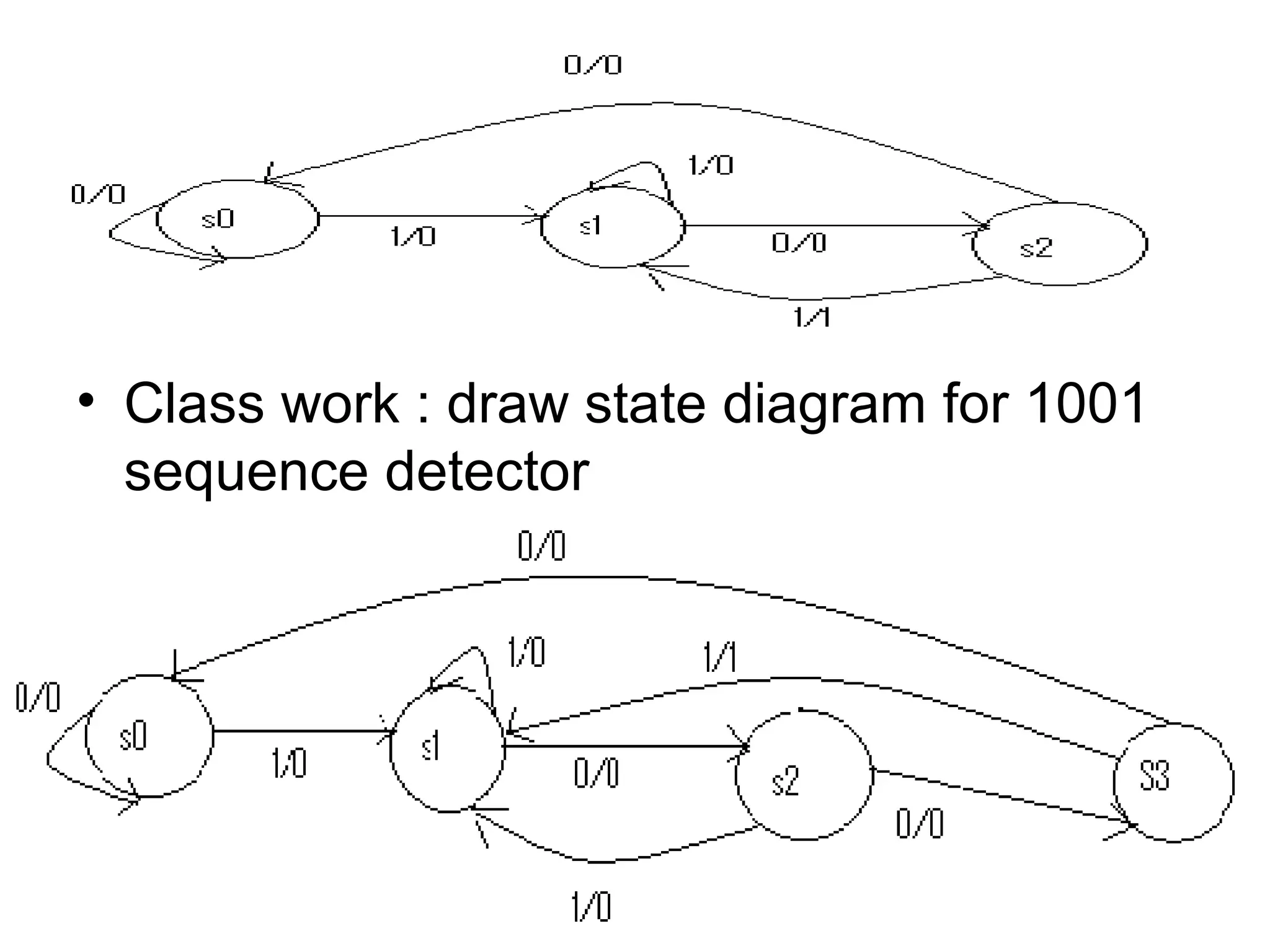
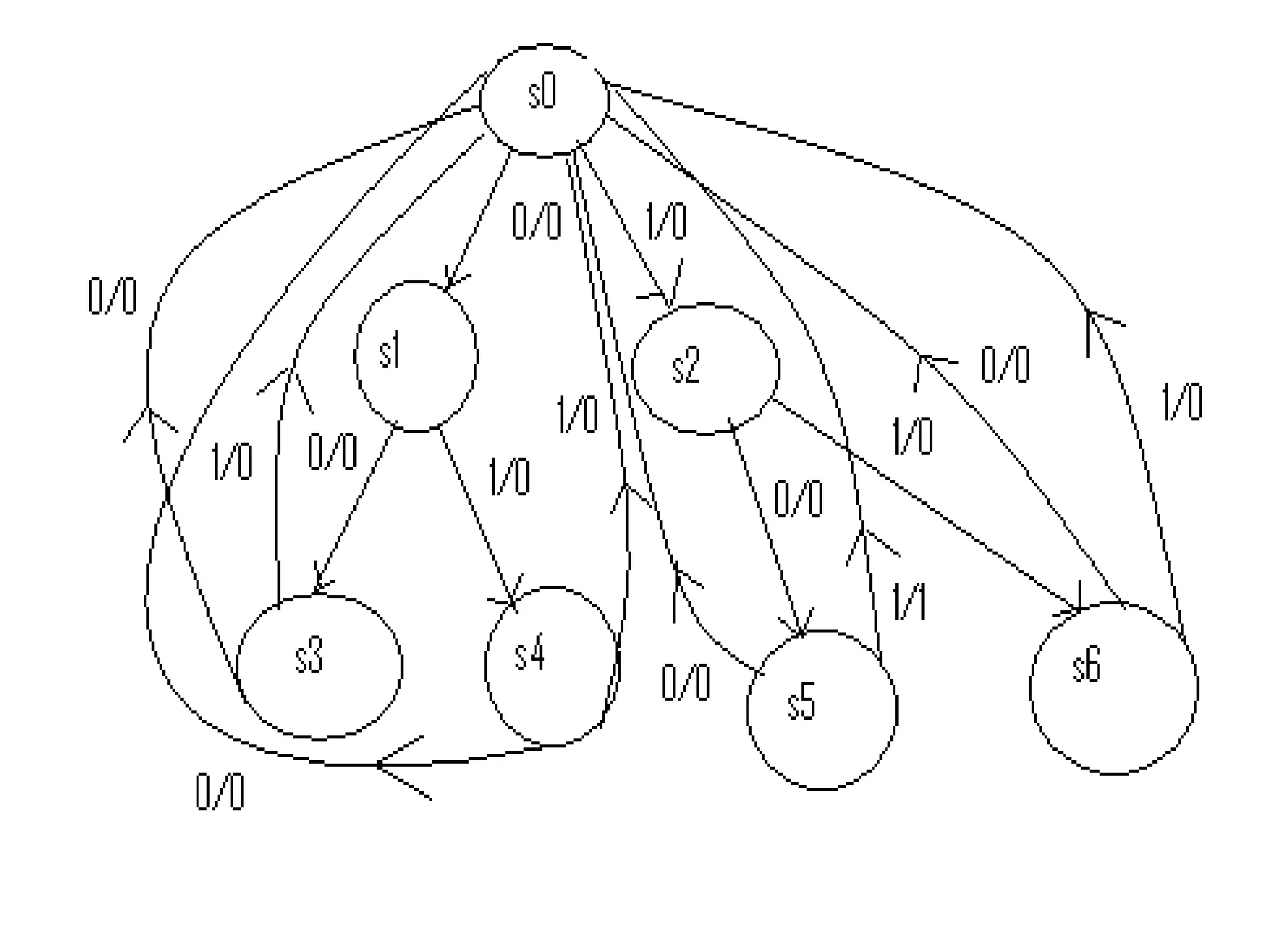
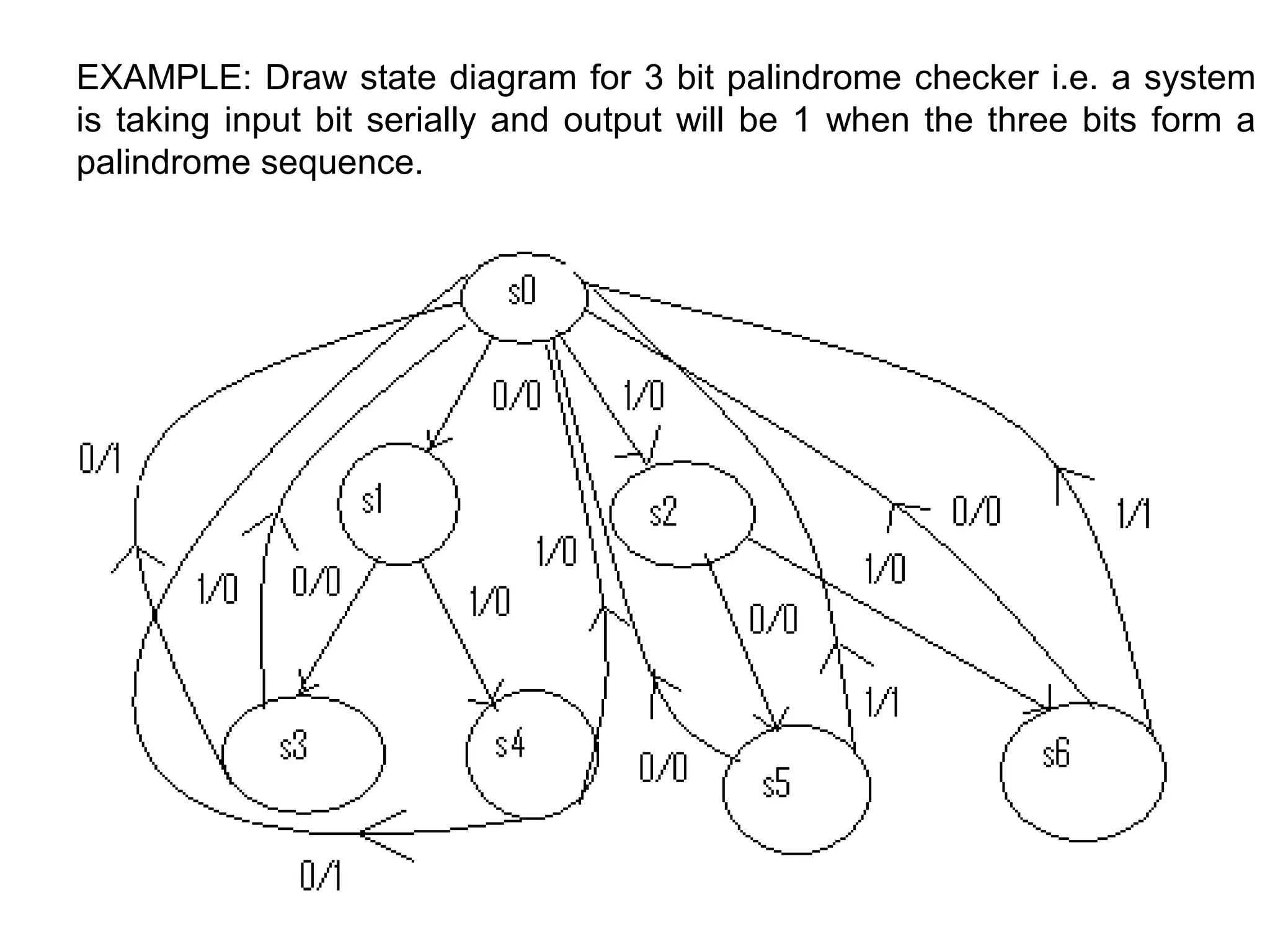
A state machine is a system that can be described by a set of states that the system transitions through. It has a set of inputs, outputs, and memory. There are two main types - Mealy machines where the output is a function of the state and inputs, and Moore machines where the output is only a function of the state. To design a state machine, you first understand the problem, draw a state diagram, reduce states if possible, assign states, and design the circuit from the state table. An example is a serial adder where each bit is added sequentially using states to track the carry.