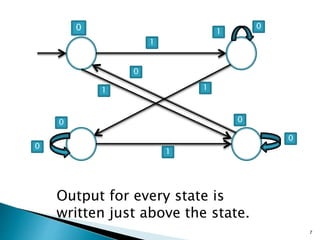
The document discusses Moore automata, which is a type of finite state machine where the next state is determined by the current state alone, independently of the input. In a Moore automata, the output at a given time depends only on the current state of the machine. It consists of 6 tuples: a finite set of states Q, input alphabet set Σ, output alphabet set Δ, transition function δ mapping state-input pairs to the next state, and output function λ mapping each state to an output. The output in response to an input string is determined by the sequence of states entered and the corresponding outputs according to λ. A Moore machine always produces an output for the empty input string based on the initial state.

1. Prof.Neeraj Bhargava
Abhishek Kumar Department of
Computer Science
School of Engineering & System Sciences,
MDS, University Ajmer, Rajasthan, India
1

2.  The Moore automata is a finite state machine
in which next state decided by current state.
 It is independent form current input symbol .
 The output at a given time only depends upon
the current state of the machine.
 This machine has 6 tuples {Q,∑,∆,∂,q0,λ}.
 Q= Finite non-empty set of states.
 ∑=set of input alphabets.
 ∆=output alphabet symbol
 ∂=Transition function mapping Q X ∑->Q
 λ =is a mapping form Q to ∆ giving output
associated with each state.
2

3.  Output in response to input a1 a2…….
an is
λ (q0) λ (q1) λ (q2) λ (q3) ….. λ (qn) .
 where q1 q2……. qn is the sequence
of state such that ∂(qi-1,ai)=qi
3

4.  NOTE :-> any Moore machine gives
output
 λ (qo) in response to input – empty
string
 If z(t) & q(t)are the output and
current state
 respectively at time t, to check
 It is more convenient in automata
theory to use Moore machine.
z(t)->q(t)* λ
4

5.  DFA may be viewed as a special
case of Moore machine where
 Output for accepting state Is 1
 Output for no accepting state is 0
5

6. next state
Present state a=0 a=1 output
-> q0 q3 q1 1
q1 q0 q3 0
q2 q2 q2 0
q3 q1 q0 1
λ (q0)=1 λ (q1)=0 λ (q2)=0 λ
(q3)=1
There is no concept of final state in
Moore machines we consider output
for each state . 6

7. q0 q1
q2 q3
Output for every state is
written just above the state.
0
1
1
0
0
1
0
0
1
0
1
0
7

8. 8