This document presents a compositional encoding of the asynchronous π-calculus (πa) into the join-calculus. It discusses the key differences between πa and the join-calculus in terms of their primitives for parallelism, communication, and restriction. It then reviews an existing encoding by Fournet and Gonthier, and Gorla's criteria for a good encoding in terms of compositionality, name invariance, and operational correspondence. The goal is to define a new encoding of πa into the join-calculus that satisfies Gorla's criteria for being a good encoding.

1. A Compositional Encoding of the Asynchronous
π-Calculus into the Join-Calculus
Stephan Mennicke† Tobias Prehn‡ Tsvetelina Yonova-Karbe‡
Institute for Programming and Reactive Systems, TU Braunschweig†
Institute for Software Engineering and Theoretical Computer Science, TU Berlin‡
September 3, 2012
YR-CONCUR 2012

2. WraP – Writing and Publishing a Scientific Paper
Supervision by Uwe Nestmann and
Kirstin Peters
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 2 / 15

3. Scope of Interest
Asynchronous π (πa ) Join-Calculus
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 3 / 15

4. Scope of Interest
Asynchronous π (πa ) Join-Calculus
P |Q Parallelism P |Q
xv Send xv
x(w).P Receive def x w | o P in . . . | o
x(w)∗ .P Recursion def x w P in . . .
x(w).P | x v Communication def x w P in x v
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 3 / 15

5. Scope of Interest
Asynchronous π (πa ) Join-Calculus
P |Q Parallelism P |Q
xv Send xv
x(w).P Receive def x w | o P in . . . | o
x(w)∗ .P Recursion def x w P in . . .
x(w).P | x v Communication def x w P in x v
Restriction
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 3 / 15

6. Scope of Interest
Asynchronous π (πa ) Join-Calculus
P |Q Parallelism P |Q
xv Send xv
x(w).P Receive def x w | o P in . . . | o
x(w)∗ .P Recursion def x w P in . . .
x(w).P | x v Communication def x w P in x v
(νx)(x(w).P | x v ) Restriction
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 3 / 15

7. Scope of Interest
Asynchronous π (πa ) Join-Calculus
P |Q Parallelism P |Q
xv Send xv
x(w).P Receive def x w | o P in . . . | o
x(w)∗ .P Recursion def x w P in . . .
x(w).P | x v Communication def x w P in x v
(νx)(x(w).P | x v ) Restriction def x w P in x v
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 3 / 15

8. Scope of Interest
Asynchronous π (πa ) Join-Calculus
P |Q Parallelism P |Q
xv Send xv
x(w).P Receive def x w | o P in . . . | o
x(w)∗ .P Recursion def x w P in . . .
x(w).P | x v Communication def x w P in x v
(νx)(x(w).P | x v ) Restriction def x w P in x v
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 3 / 15

9. Scope of Interest
π
Asynchronous π (πa ) j Join-Calculus
P |Q Parallelism P |Q
xv Send xv
x(w).P Receive def x w | o P in . . . | o
x(w)∗ .P Recursion def x w P in . . .
x(w).P | x v Communication def x w P in x v
(νx)(x(w).P | x v ) Restriction def x w P in x v
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 3 / 15

10. An Encoding is Non-Trivial
|
no (νx)
xv
x(w)
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 4 / 15

11. An Encoding is Non-Trivial
|
no (νx)
xv
x(w)
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 4 / 15

12. An Encoding is Non-Trivial
| |
no (νx)
xv xv
x(w) def x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 4 / 15

13. An Encoding is Non-Trivial
| |
no (νx)
xv xv
x(w) def x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 4 / 15

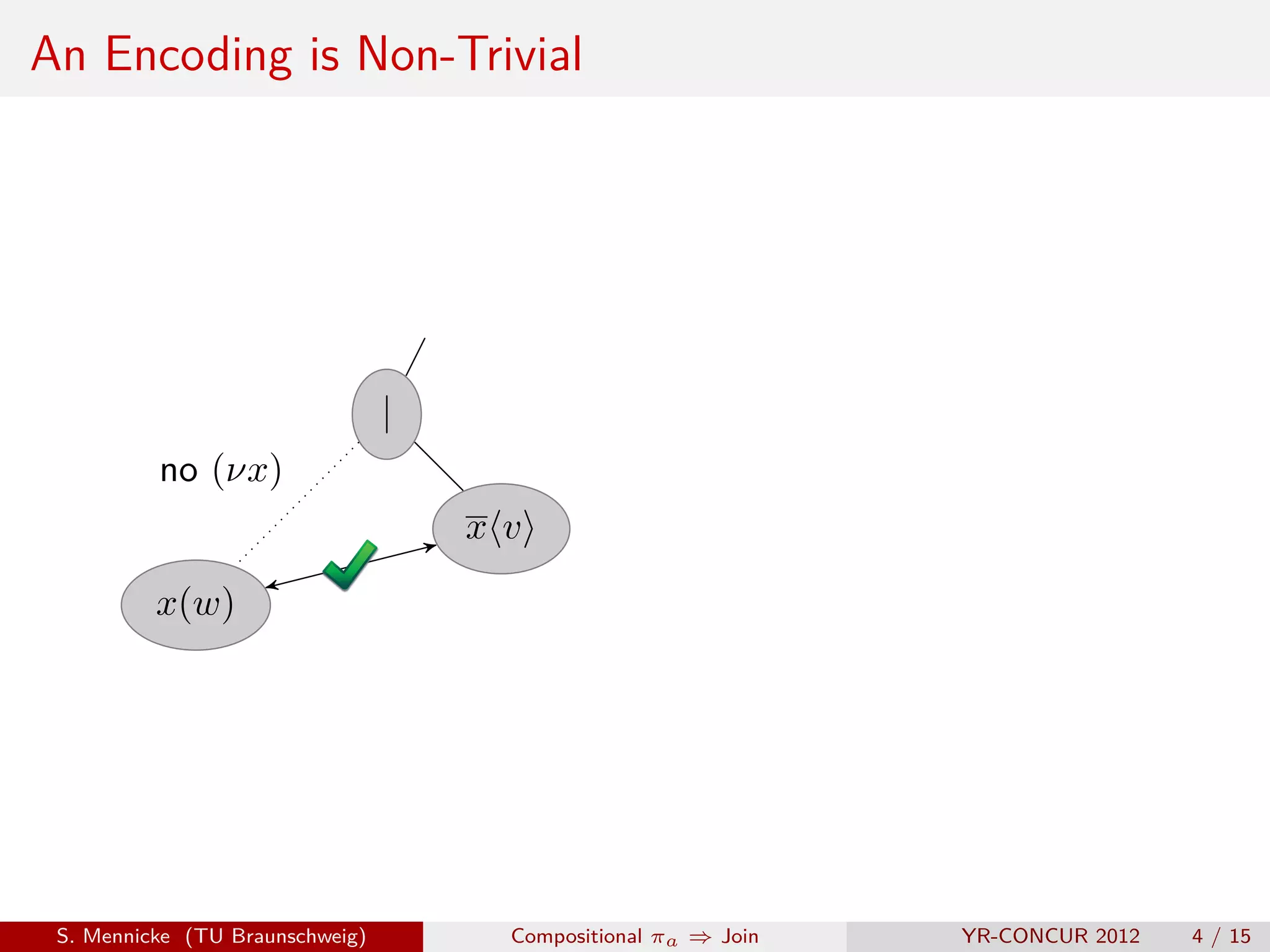
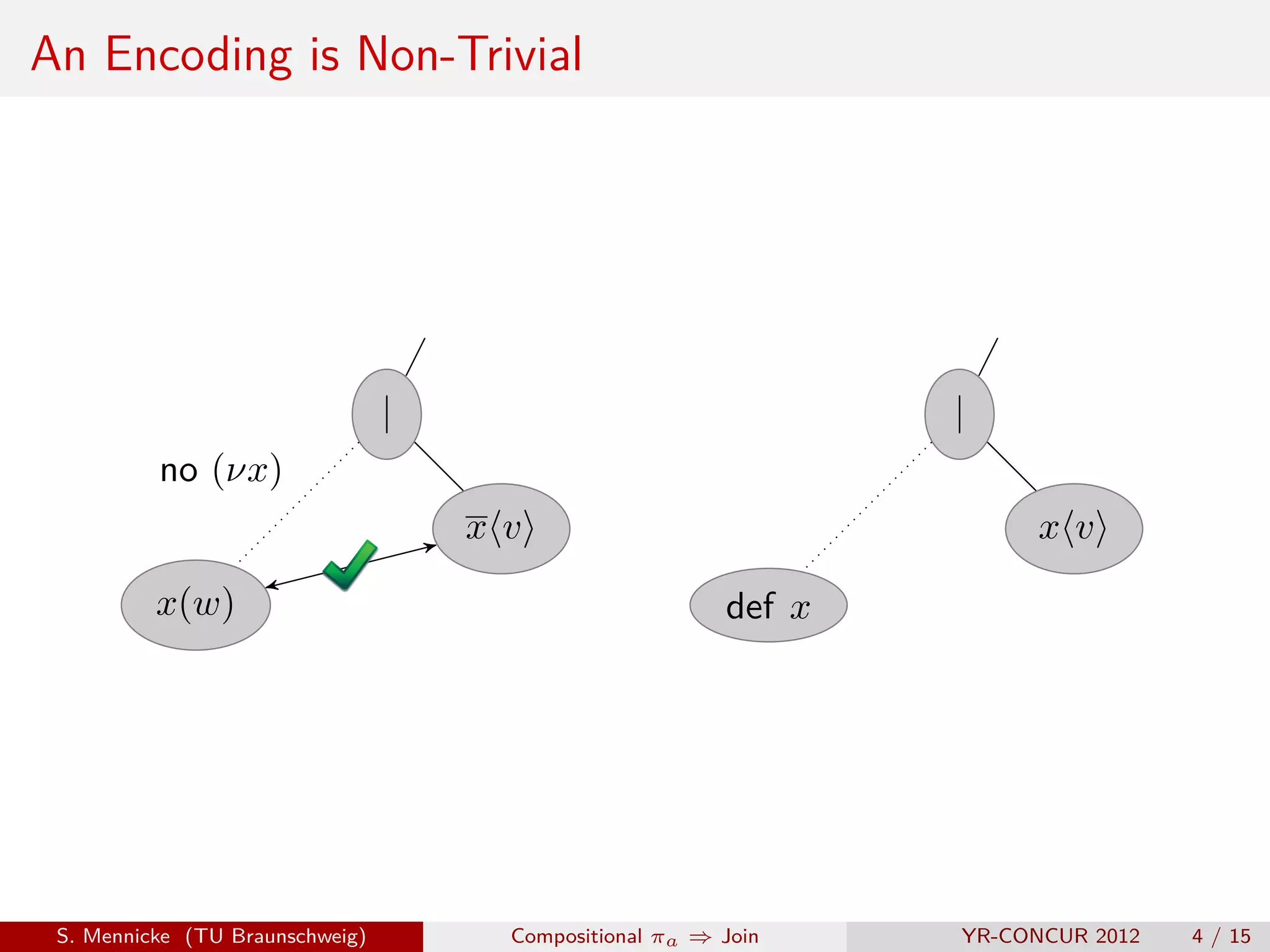
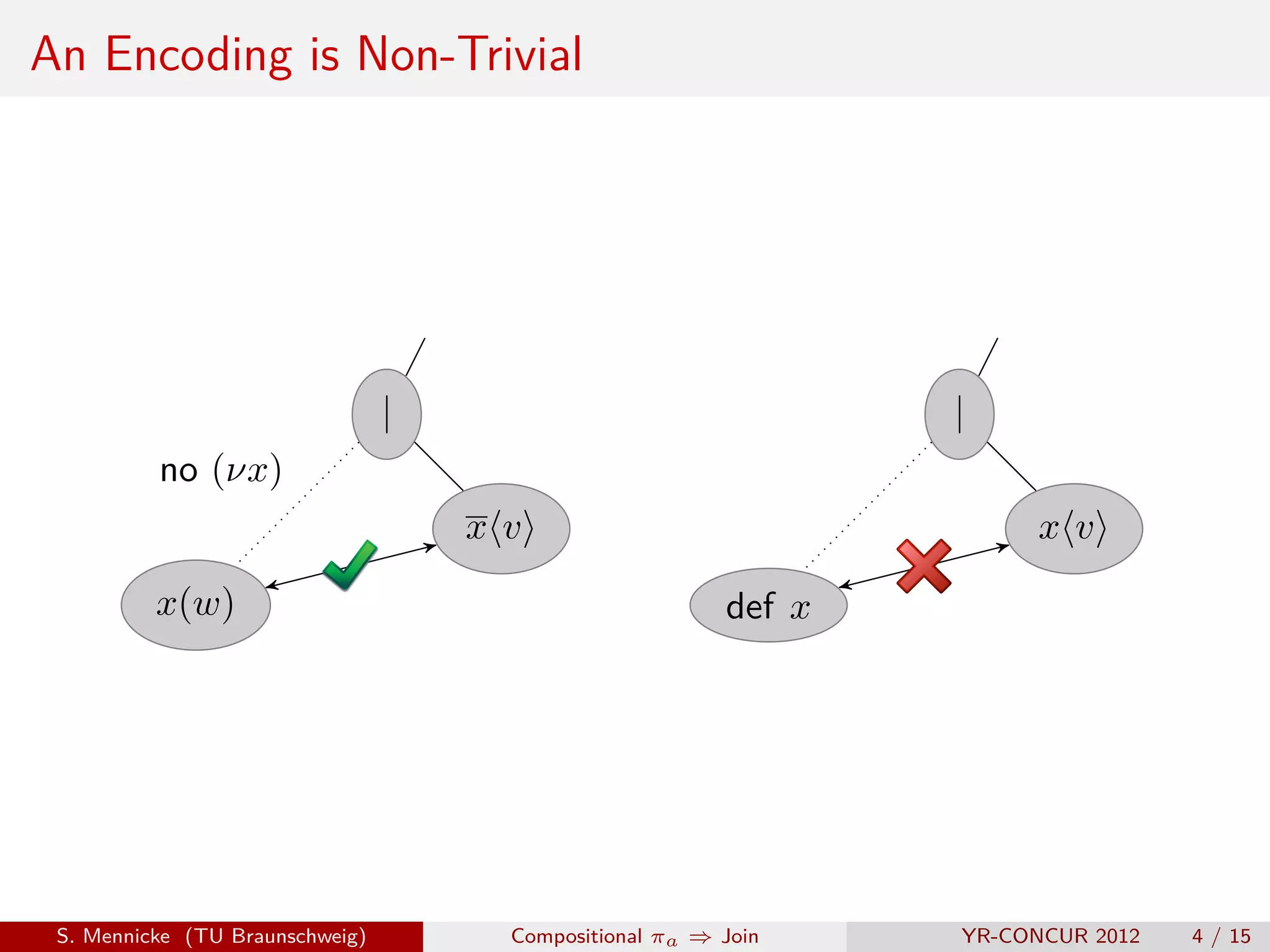
14. The Encoding of Fournet and Gonthier
[Fournet and Gonthier(1996)]
First Layer
Second Layer
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 5 / 15

15. The Encoding of Fournet and Gonthier
[Fournet and Gonthier(1996)]
First Layer
x v → xo v
P |Q → P |Q
Second Layer
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 5 / 15

16. The Encoding of Fournet and Gonthier
[Fournet and Gonthier(1996)]
First Layer
x v → xo v
P |Q → P |Q
x(w).P → def κ P in xi
Second Layer
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 5 / 15

17. The Encoding of Fournet and Gonthier
[Fournet and Gonthier(1996)]
First Layer
x v → xo v
P |Q → P |Q
x(w).P → def κ P in xi
(νx)P → def xi | xo κ in P
Second Layer
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 5 / 15

18. The Encoding of Fournet and Gonthier
[Fournet and Gonthier(1996)]
First Layer
x v → xo v
P |Q → P |Q
x(w).P → def κ P in xi
(νx)P → def xi | xo κ in P
Second Layer
Restrict all free names
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 5 / 15

19. The Encoding of Fournet and Gonthier
[Fournet and Gonthier(1996)]
First Layer
x v → xo v
P |Q → P |Q
x(w).P → def κ P in xi
(νx)P → def xi | xo κ in P
Second Layer
Restrict all free names
Is this good?
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 5 / 15

20. Gorla’s Criteria for Good Encodings [Gorla(2010)]
.
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 6 / 15

21. Gorla’s Criteria for Good Encodings [Gorla(2010)]
I. Compositionality
.
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 6 / 15

22. Gorla’s Criteria for Good Encodings [Gorla(2010)]
I. Compositionality
.
II. Name Invariance
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 6 / 15

23. Gorla’s Criteria for Good Encodings [Gorla(2010)]
I. Compositionality
Syntactic Criteria
.
II. Name Invariance
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 6 / 15

24. Gorla’s Criteria for Good Encodings [Gorla(2010)]
I. Compositionality
Syntactic Criteria
.
II. Name Invariance
III. Operational Correspondence
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 6 / 15

25. Gorla’s Criteria for Good Encodings [Gorla(2010)]
I. Compositionality
Syntactic Criteria
.
IV. Divergence Reflection II. Name Invariance
III. Operational Correspondence
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 6 / 15

26. Gorla’s Criteria for Good Encodings [Gorla(2010)]
V. Success Sensitiveness I. Compositionality
Syntactic Criteria
.
IV. Divergence Reflection II. Name Invariance
III. Operational Correspondence
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 6 / 15

27. Gorla’s Criteria for Good Encodings [Gorla(2010)]
V. Success Sensitiveness I. Compositionality
Syntactic Criteria
Semantic Criteria
.
IV. Divergence Reflection II. Name Invariance
III. Operational Correspondence
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 6 / 15

28. Fournet and Gonthier’s Encoding Revisited
First level encoding is compositional and operationally correspondent
for closed terms
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 7 / 15

29. Fournet and Gonthier’s Encoding Revisited
First level encoding is compositional and operationally correspondent
for closed terms
First level encoding is not operationally correspondent for open
terms
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 7 / 15

30. Fournet and Gonthier’s Encoding Revisited
First level encoding is compositional and operationally correspondent
for closed terms
First level encoding is not operationally correspondent for open
terms
First+Second level encoding is not compositional
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 7 / 15

31. Fournet and Gonthier’s Encoding Revisited
First level encoding is compositional and operationally correspondent
for closed terms
First level encoding is not operationally correspondent for open
terms
First+Second level encoding is not compositional
Our Approach
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 7 / 15

32. Fournet and Gonthier’s Encoding Revisited
First level encoding is compositional and operationally correspondent
for closed terms
First level encoding is not operationally correspondent for open
terms
First+Second level encoding is not compositional
Our Approach
We introduce send/receive requests carrying the channel names
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 7 / 15

33. Fournet and Gonthier’s Encoding Revisited
First level encoding is compositional and operationally correspondent
for closed terms
First level encoding is not operationally correspondent for open
terms
First+Second level encoding is not compositional
Our Approach
We introduce send/receive requests carrying the channel names
We keep the main idea of restriction
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 7 / 15

34. Fournet and Gonthier’s Encoding Revisited
First level encoding is compositional and operationally correspondent
for closed terms
First level encoding is not operationally correspondent for open
terms
First+Second level encoding is not compositional
Our Approach
We introduce send/receive requests carrying the channel names
We keep the main idea of restriction
We implement a protocol to handle communication
[Peters and Nestmann(2011)]
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 7 / 15

35. Fournet and Gonthier’s Encoding Revisited
First level encoding is compositional and operationally correspondent
for closed terms
First level encoding is not operationally correspondent for open
terms
First+Second level encoding is not compositional
Our Approach
We introduce send/receive requests carrying the channel names
We keep the main idea of restriction
We implement a protocol to handle communication
[Peters and Nestmann(2011)]
We need matching to decide which requests may cooperate
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 7 / 15

36. The Big Picture
π
(1) x v j = def lf t, f | f alse f | f alse in
(2) def lt t, f | true t | f alse in
(3) def l t, f lt t, f | lf t, f in sr x, v, l | true
π
(4) P |Q j = def rrτ c, k | trans0 m m c, k | trans0 m in
(5) def chain trans0 | srτ c, v, l
(6) def mup c, k | trans m m c, k | trans m in
(7) def m c , k
(8) [c = c ]k v, l | mup c , k
(9) in trans0 m | chain trans
(10) in chain trans0 |
(11) def sr c, v, l srup c, v, l | srτ c, v, l in
(12) def srup c, v, l sr c, v, l in
(13) def rr c, k rrup c, k | rrτ c, k in
(14) def rrup c, k rr c, k in
(15) P π | Q π
j j
π
(16) x(v).P j = def k v, l | once
(17) def t P π in
j
(18) def f once in l t, f
(19) in rr x, k | once
π
(20) (νx)P j = def x 0 in P π j
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 8 / 15

37. What our Encoding does
P = (νx)(y a | x(u).Q) | x b | y(z).R
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 9 / 15

38. What our Encoding does
P = (νx)(y a | x(u).Q) | x b | y(z).R
|
νx |
| x y
y x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 9 / 15

39. What our Encoding does
P = (νx)(y a | x(u).Q) | x b | y(z).R
|
νx |
| x x y y
y y x x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 9 / 15

40. What our Encoding does
P = (νx)(y a | x(u).Q) | x b | y(z).R
|
νx |
| y x x y y
y x x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 9 / 15

41. What our Encoding does
P = (νx)(y a | x(u).Q) | x b | y(z).R
| y
νx |
| y x x y y
y x x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 9 / 15

42. What our Encoding does
P = (νx)(y a | x(u).Q) | x b | y(z).R
| y
νx |
| y x x x y y
y x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 9 / 15

43. What our Encoding does
P = (νx)(y a | x(u).Q) | x b | y(z).R
| y x
νx |
| y x x x y y
y x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 9 / 15

44. What our Encoding does
P = (νx)(y a | x(u).Q) | x b | y(z).R
| y
νx | x
| y x x y y
y x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 9 / 15

45. What our Encoding does
P = (νx)(y a | x(u).Q) | x b | y(z).R
| y
νx | x y
| y x x y
y x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 9 / 15

46. What our Encoding does
P = (νx)(y a | x(u).Q) | x b | y(z).R
| y y
νx | x y
| y x x y
y x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 9 / 15

47. What our Encoding does
P = (νx)(y a | x(u).Q) | x b | y(z).R
| y y
x
νx | x y
| y x x y
y x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 9 / 15

48. What our Encoding does
P = (νx)(y a | x(u).Q) | x b | y(z).R
| y y
x
νx | x y
| y x x y
y x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 9 / 15

49. What our Encoding does
P = (νx)(y a | x(u).Q) | x b | y(z).R
| y y
x
νx | x y
| y x x y
y x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 9 / 15

50. What our Encoding does
P = (νx)(y a | x(u).Q) | x b | y(z).R
| y y
x
νx | x y
| y x x y
y x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 9 / 15

51. A Receive Requests (x(v).P )
x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 10 / 15

52. A Receive Requests (x(v).P )
def k
rr x, k
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 10 / 15

53. A Receive Requests (x(v).P )
rr x, k
def k
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 10 / 15

54. A Receive Requests (x(v).P )
def k
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 10 / 15

55. A Receive Requests (x(v).P )
k v, l
def k
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 10 / 15

56. A Receive Requests (x(v).P )
k v, l
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 10 / 15

57. A Receive Requests (x(v).P )
if l then P
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 10 / 15

58. B Send Requests (x v )
x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 11 / 15

59. B Send Requests (x v )
def l
sr x, v, l
true
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 11 / 15

60. B Send Requests (x v )
sr x, v, l
def l
true
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 11 / 15

61. B Send Requests (x v )
def l
true
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 11 / 15

62. B Send Requests (x v )
l t, f
def l
true
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 11 / 15

63. B Send Requests (x v )
t
def l
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 11 / 15

64. B Send Requests (x v )
l t, f
def l
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 11 / 15

65. B Send Requests (x v )
f
def l
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 11 / 15

66. C Restriction (νx)
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 12 / 15

67. C Restriction (νx)
¬x
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 12 / 15

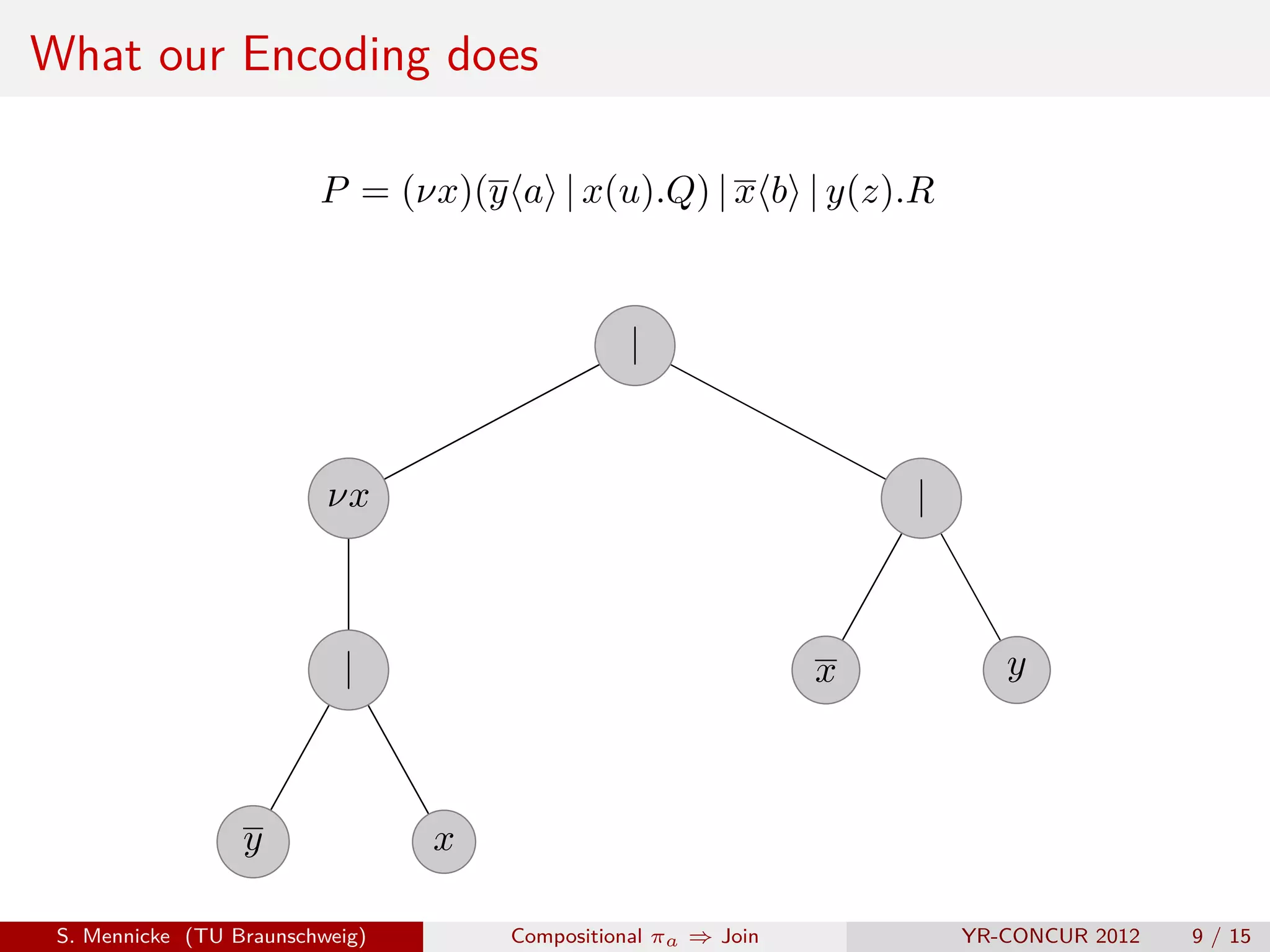
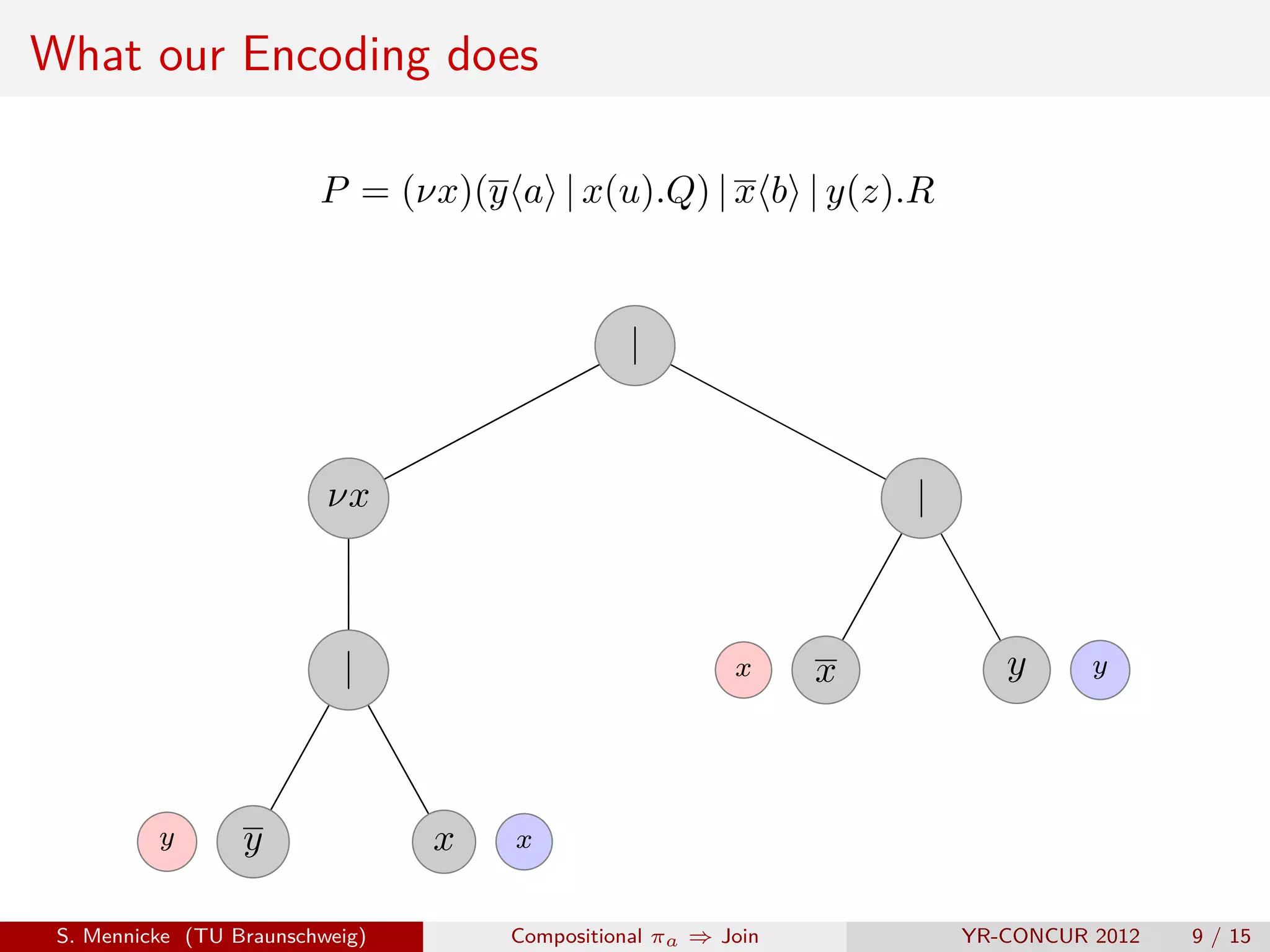
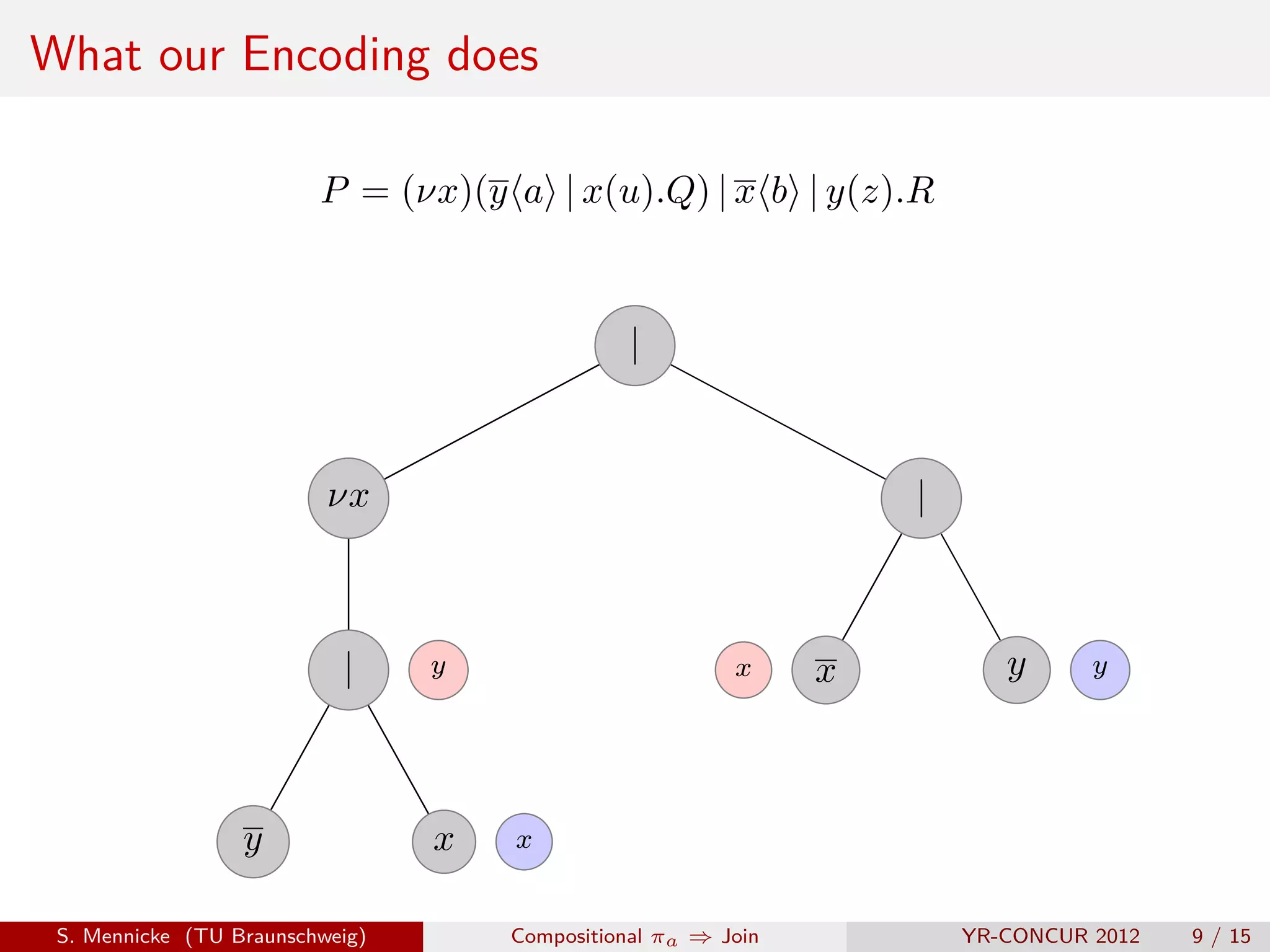
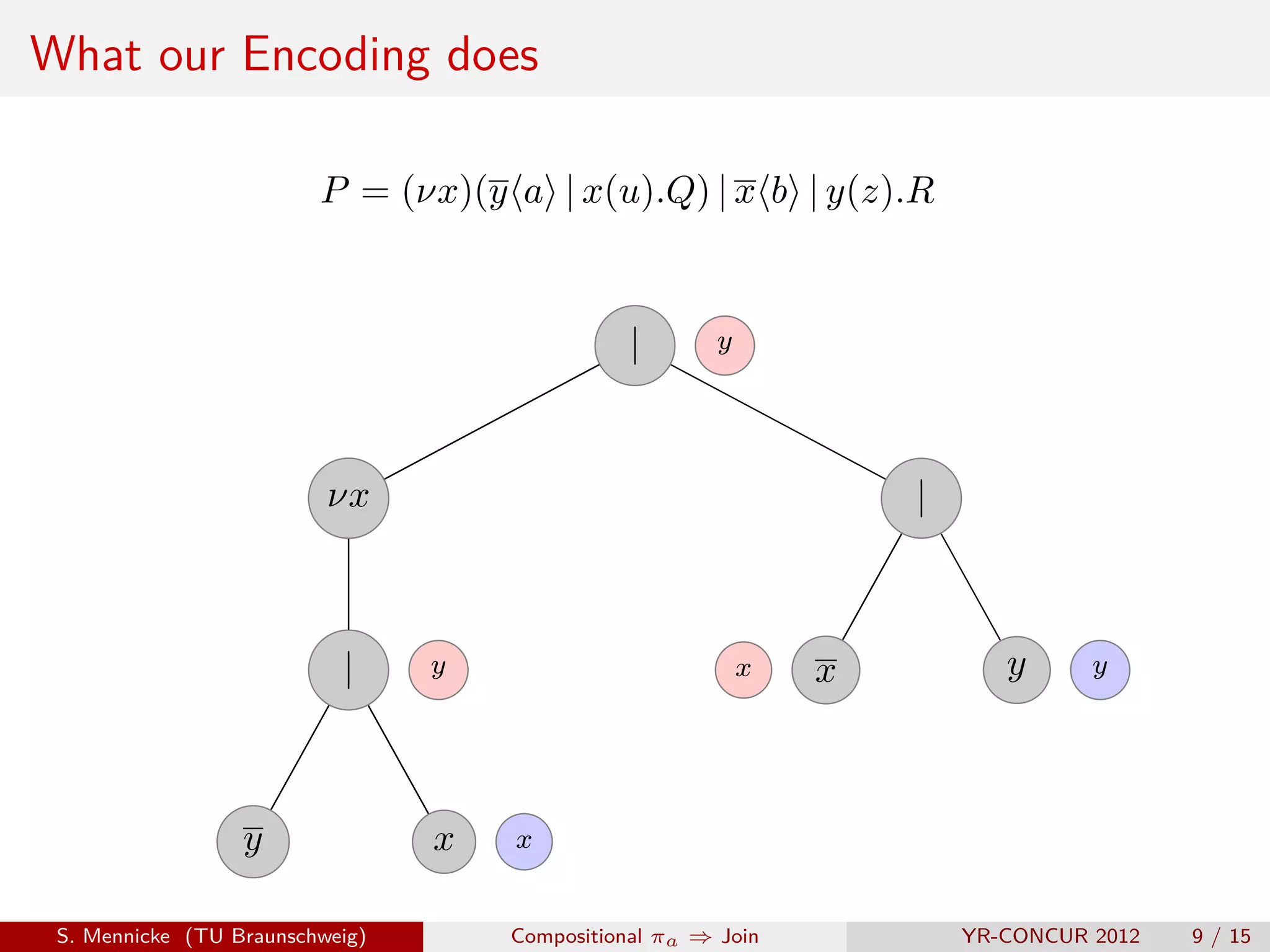
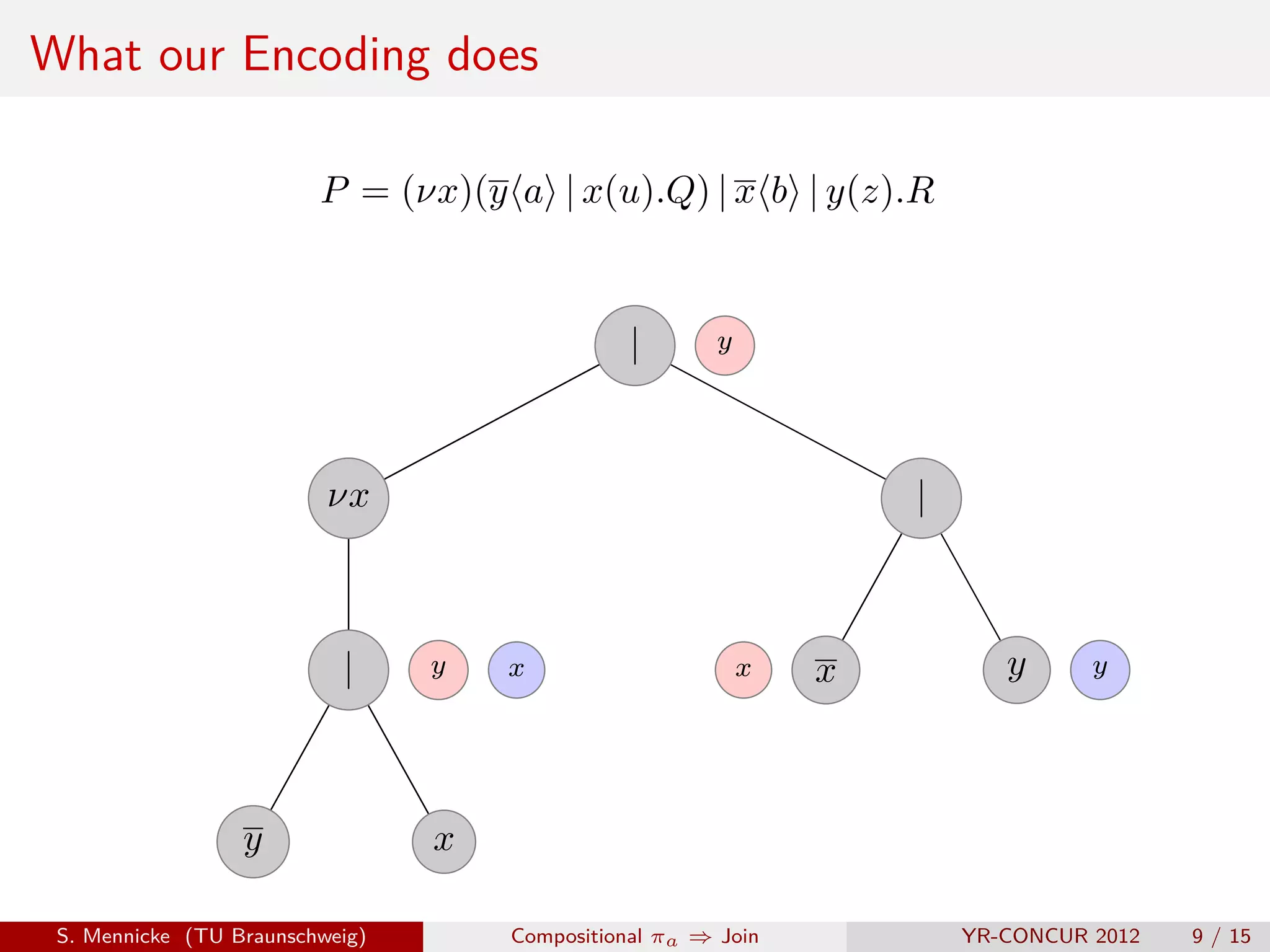
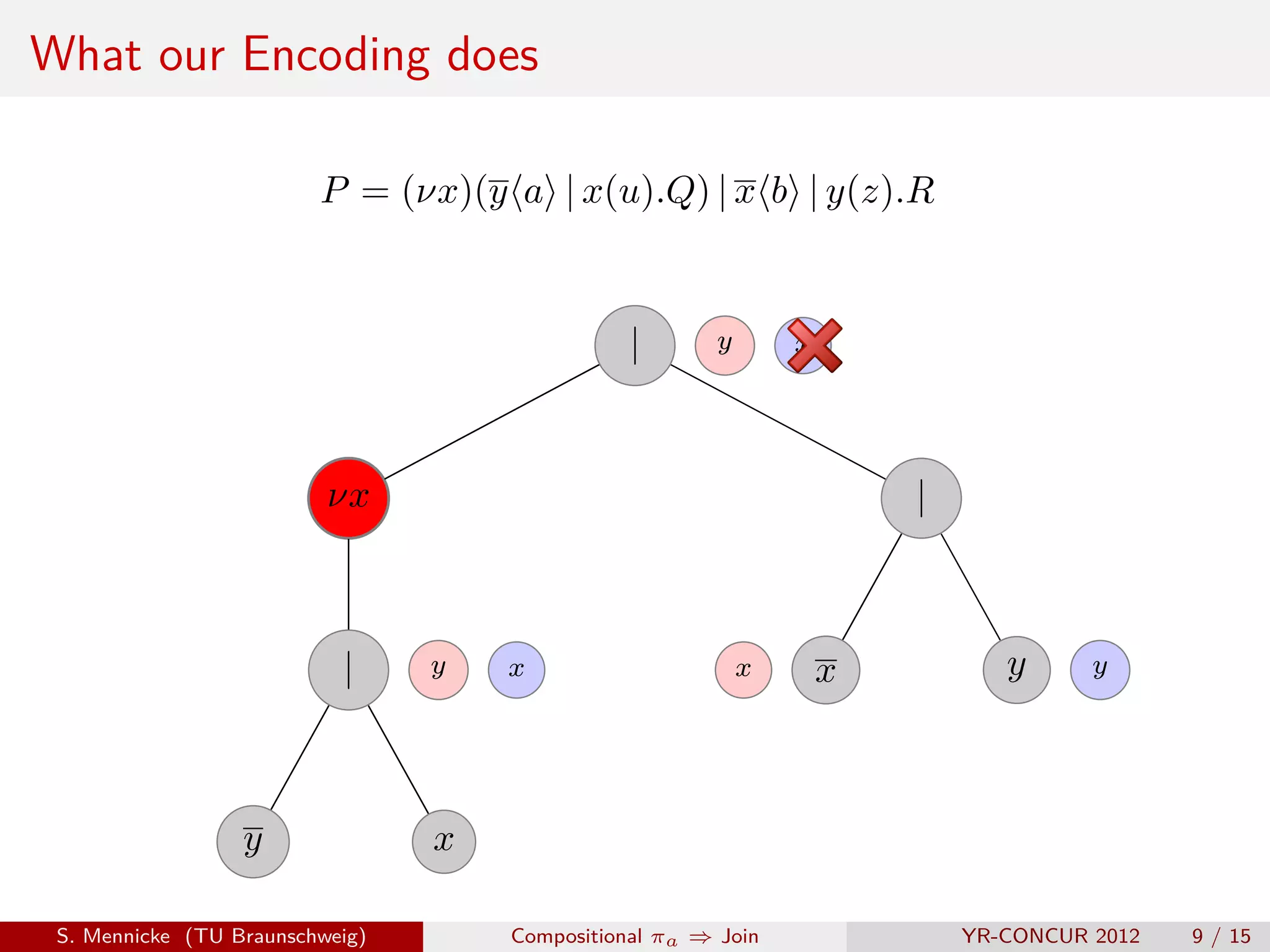
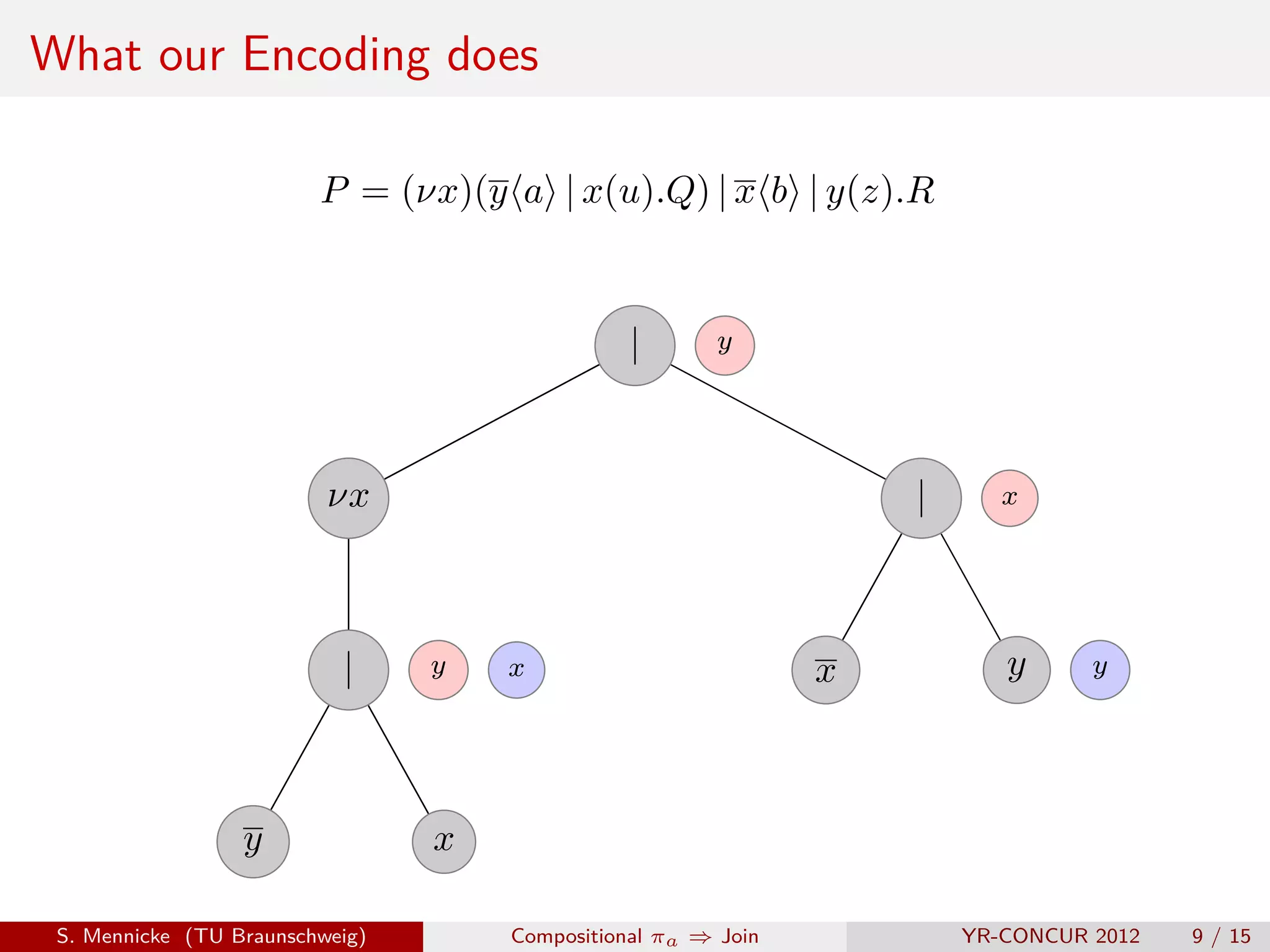
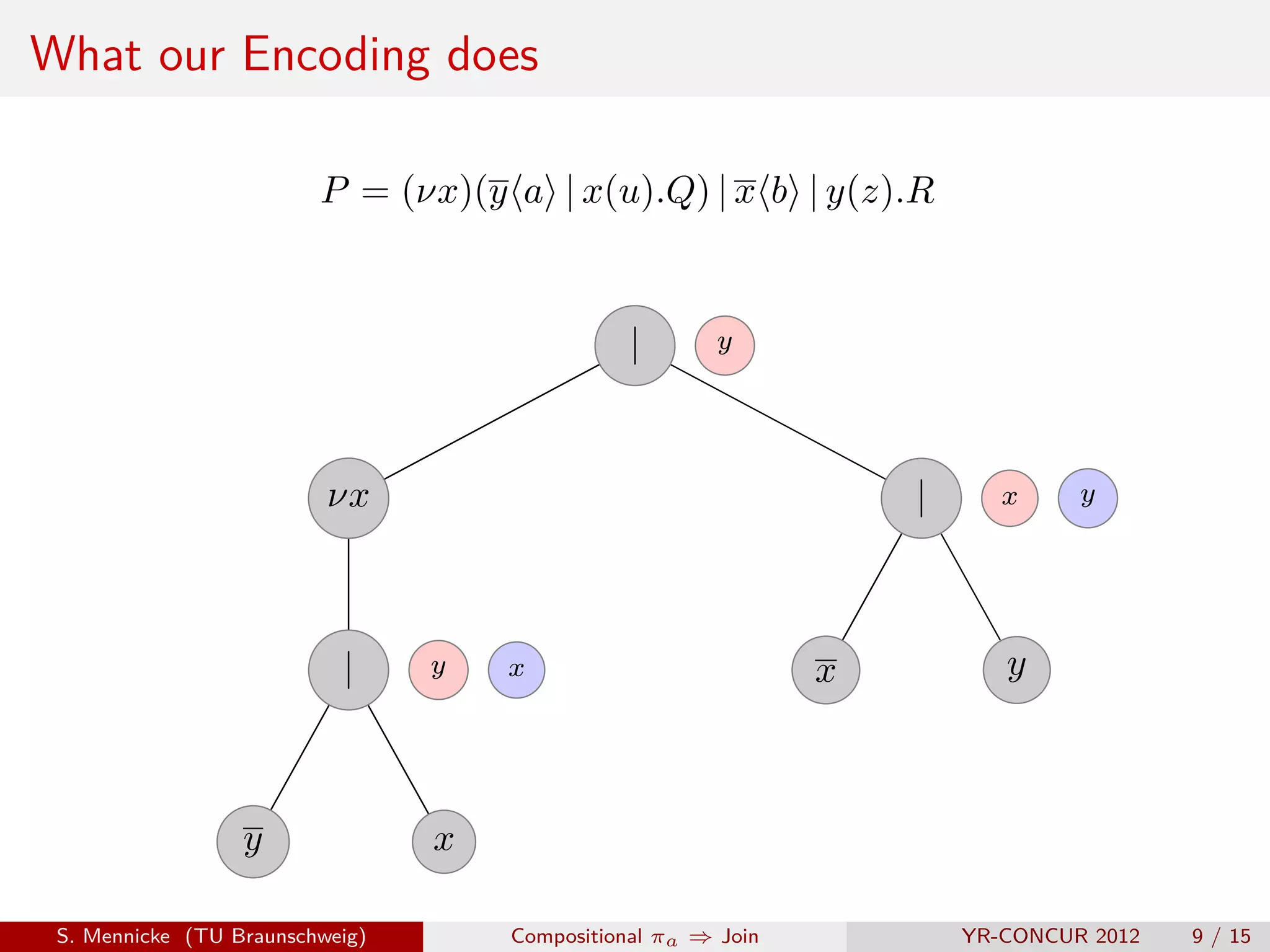
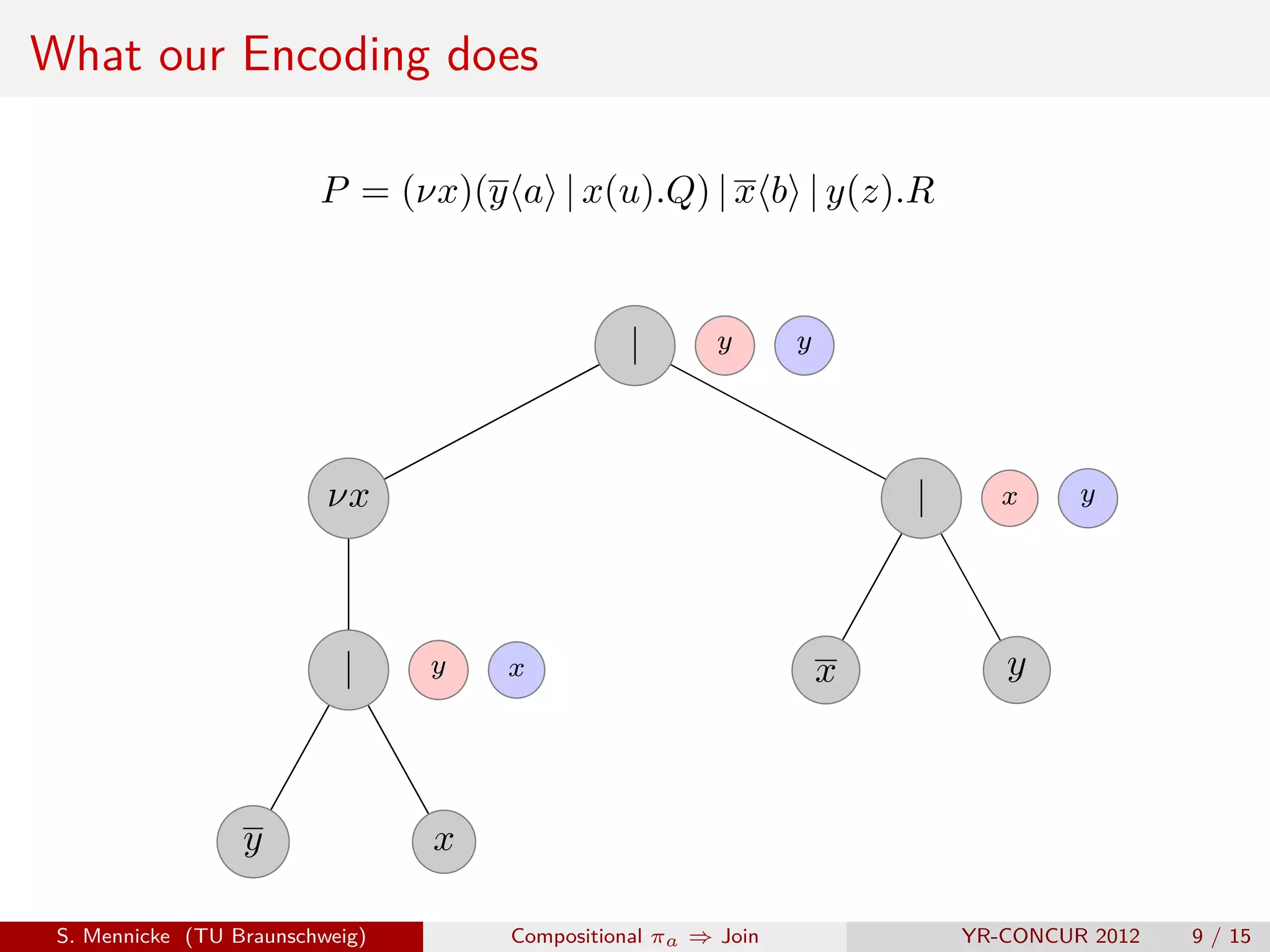
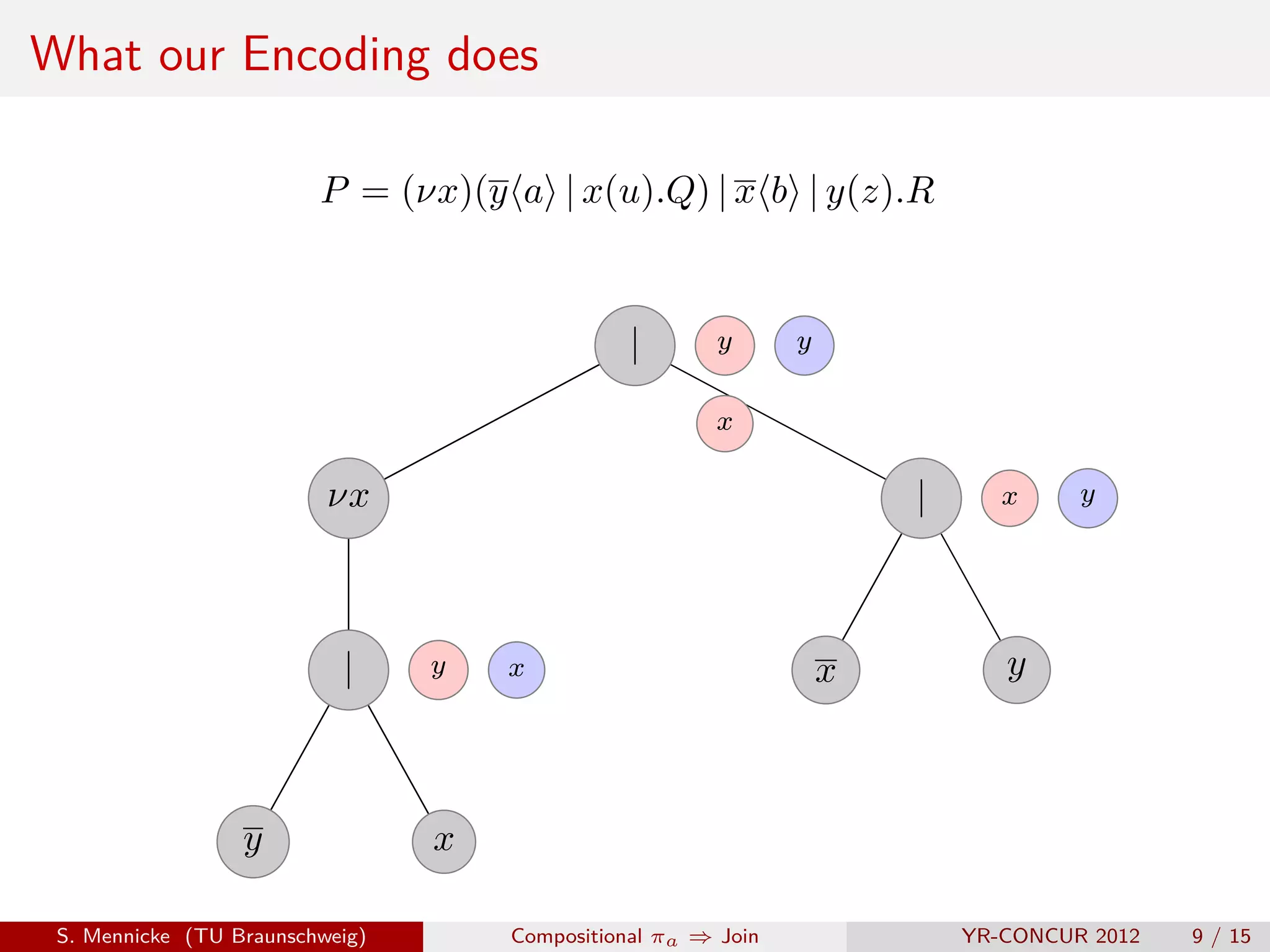
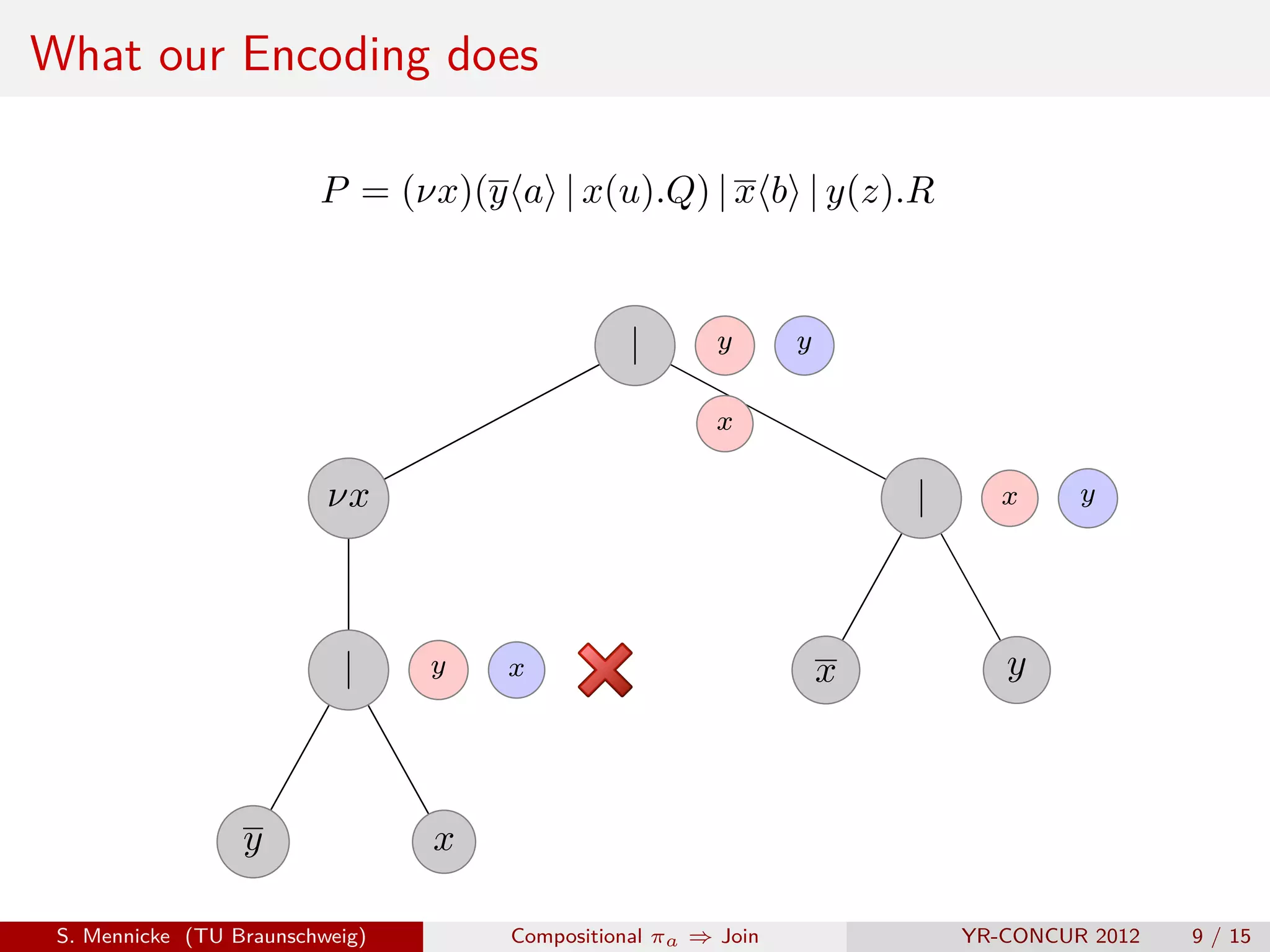
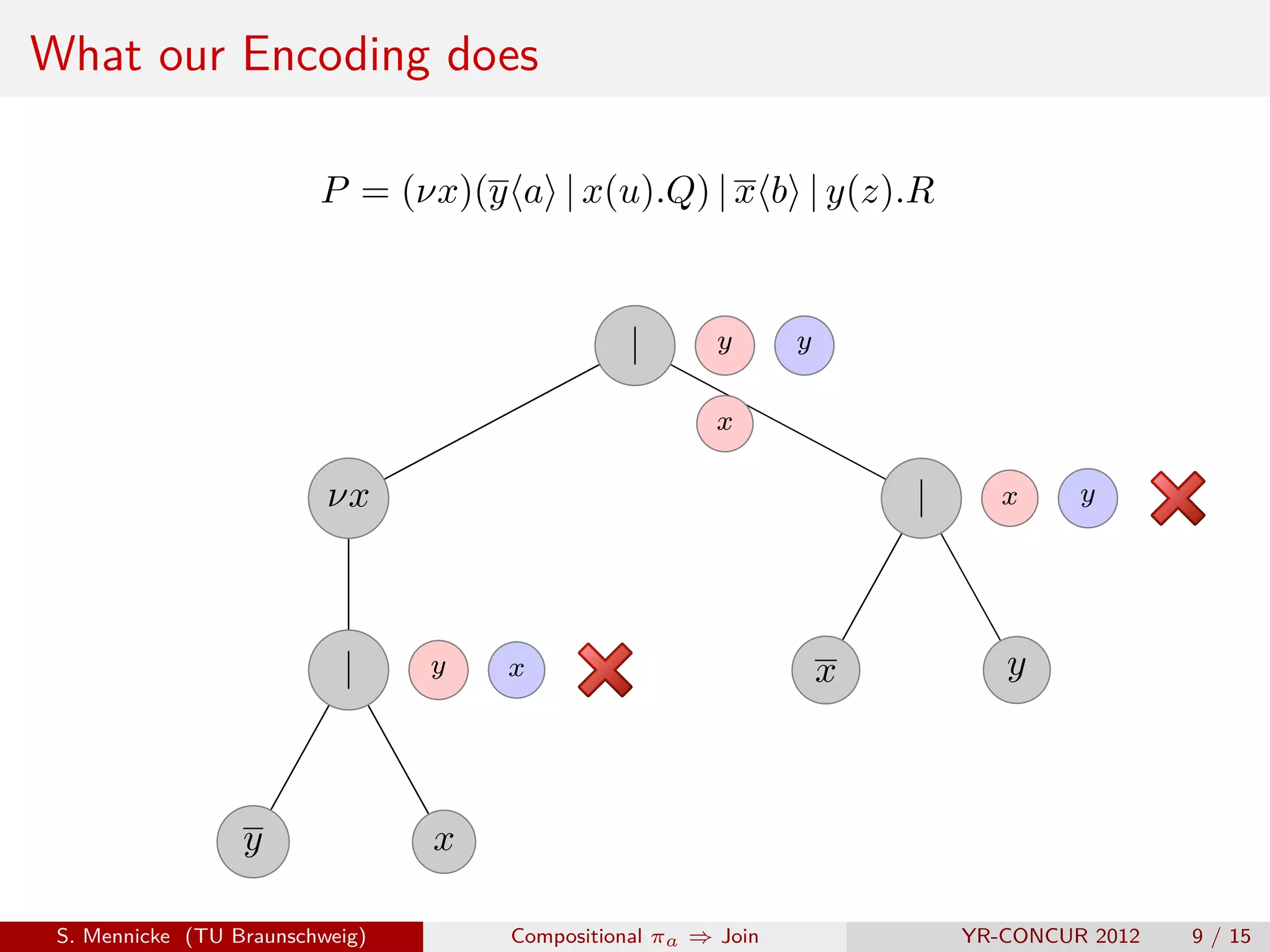
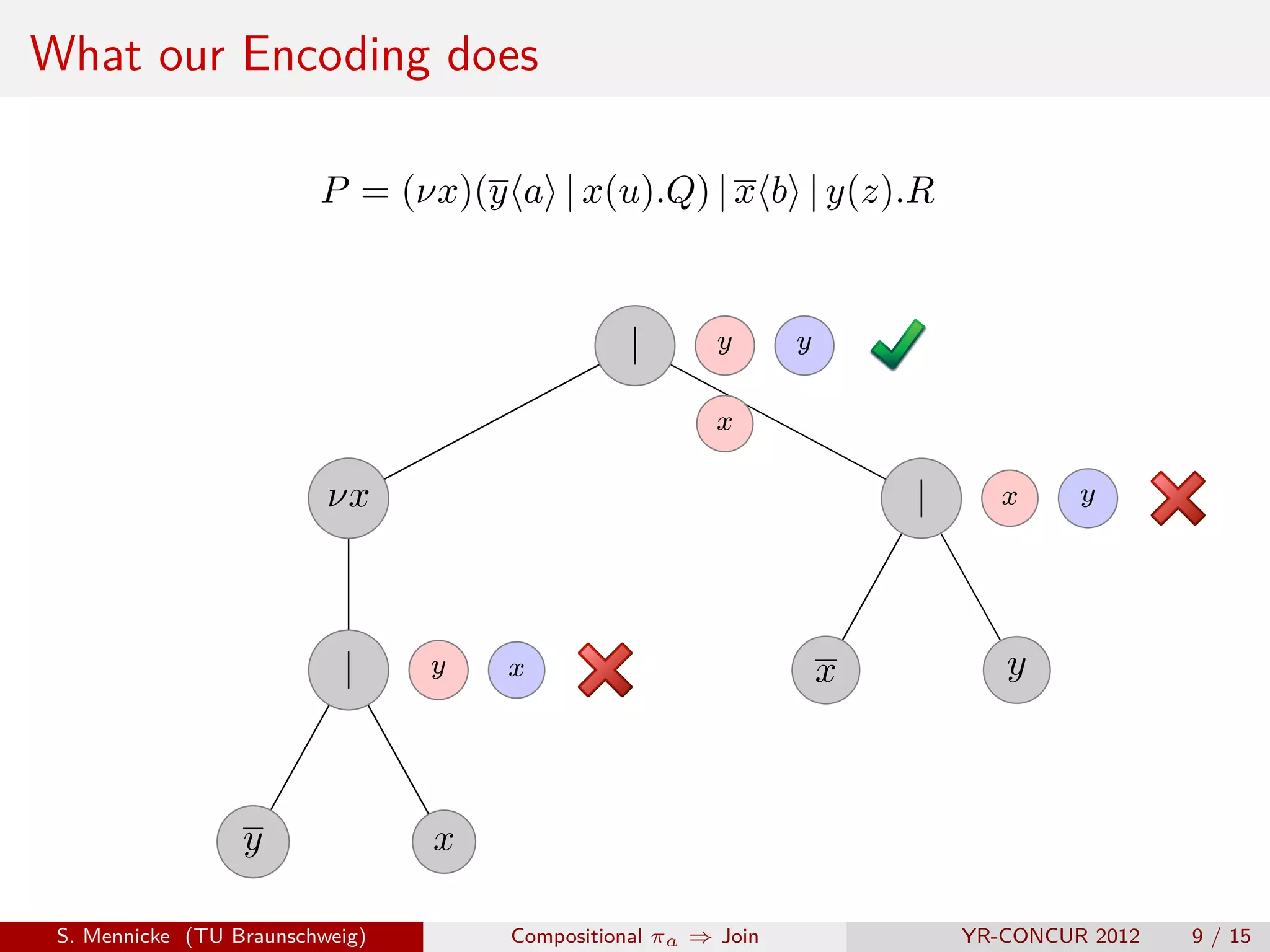
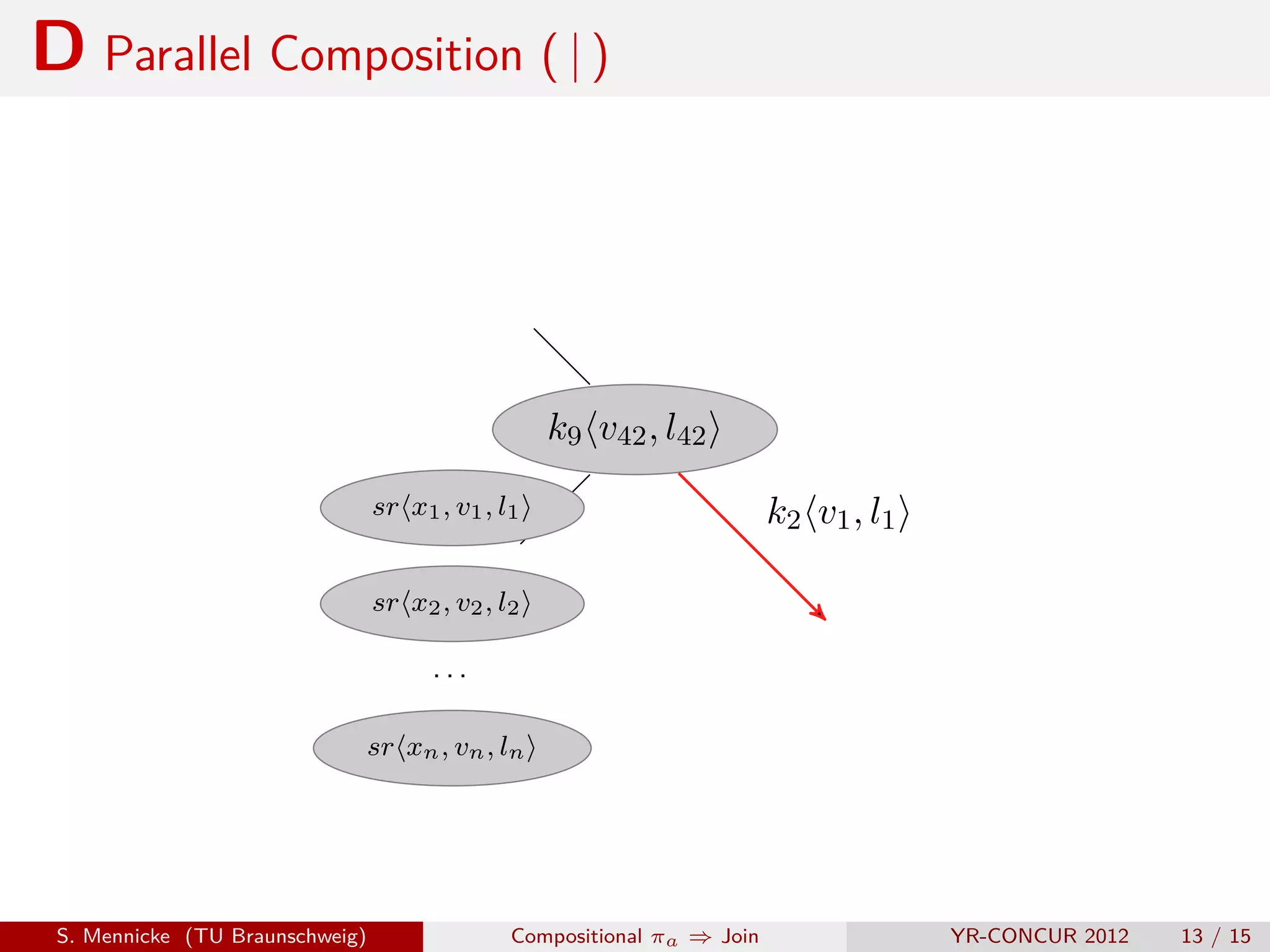
68. D Parallel Composition ( | )
Remember this?
π
P |Q j = def rrτ c, k | trans0 m m c, k | trans0 m in
def chain trans0 | srτ c, v, l
def mup c, k | trans m m c, k | trans m in
def m c , k
[c = c ]k v, l | mup c , k
in trans0 m | chain trans
in chain trans0 |
def sr c, v, l srup c, v, l | srτ c, v, l in
def srup c, v, l sr c, v, l in
def rr c, k rrup c, k | rrτ c, k in
def rrup c, k rr c, k in
P π | Q π
j j
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 13 / 15

69. D Parallel Composition ( | )
|
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 13 / 15

70. D Parallel Composition ( | )
|
sr x1 , v1 , l1
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 13 / 15

71. D Parallel Composition ( | )
|
rr y1 , k1
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 13 / 15

72. D Parallel Composition ( | )
sr x1 , v1 , l1 , . . . , sr xn , vn , ln
rr y1 , k1 , . . . , rr yn , kn
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 13 / 15

73. D Parallel Composition ( | )
sr/rr
sr x1 , v1 , l1 , . . . , sr xn , vn , ln
rr y1 , k1 , . . . , rr yn , kn
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 13 / 15

74. D Parallel Composition ( | )
sr x1 , v1 , l1 , . . . , sr xn , vn , ln
rr y1 , k1 , . . . , rr yn , kn
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 13 / 15

75. D Parallel Composition ( | )
sr x1 , v1 , l1 , . . . , sr xn , vn , ln
rr y1 , k1 , . . . , rr yn , kn
sr x1 , v1 , l1
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 13 / 15

76. D Parallel Composition ( | )
sr x1 , v1 , l1 , . . . , sr xn , vn , ln
rr y1 , k1 , . . . , rr yn , kn
sr x1 , v1 , l1
sr x2 , v2 , l2
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 13 / 15

77. D Parallel Composition ( | )
rr y1 , k1 , . . . , rr yn , kn
sr x1 , v1 , l1
sr x2 , v2 , l2
...
sr xn , vn , ln
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 13 / 15

78. D Parallel Composition ( | )
rr y1 , k1 , . . . , rr yn , kn
sr x1 , v1 , l1 rr yi , ki if x1 = yi then ki v1 , l1
sr x2 , v2 , l2
...
sr xn , vn , ln
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 13 / 15

79. D Parallel Composition ( | )
rr y1 , k1 , . . . , rr yn , kn
sr x1 , v1 , l1
sr x2 , v2 , l2 rr yi , ki if x2 = yi then ki v2 , l2
...
sr xn , vn , ln
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 13 / 15

80. D Parallel Composition ( | )
k2 v1 , l1 , k9 v42 , l42
sr x1 , v1 , l1
sr x2 , v2 , l2
...
sr xn , vn , ln
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 13 / 15

81. D Parallel Composition ( | )
k9 v42 , l42
sr x1 , v1 , l1 k2 v1 , l1
sr x2 , v2 , l2
...
sr xn , vn , ln
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 13 / 15

82. Take-Home-Points
1 There is a good encoding from πa to Join: ours!
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 14 / 15

83. Take-Home-Points
1 There is a good encoding from πa to Join: ours!
2 It is compositional
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 14 / 15

84. Take-Home-Points
1 There is a good encoding from πa to Join: ours!
2 It is compositional
3 Strong Conjecture: It is operationally correspondent
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 14 / 15

85. Take-Home-Points
1 There is a good encoding from πa to Join: ours!
2 It is compositional
3 Strong Conjecture: It is operationally correspondent
Thank you!
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 14 / 15

86. Bibliography
Cédric Fournet and Georges Gonthier.
The reflexive chemical abstract machine and the join-calculus.
pages 372–385, 1996.
D. Gorla.
Towards a Unified Approach to Encodability and Separation Results
for Process Calculi.
Information and Computation, 208(9) 1031–1053, 2010.
K. Peters and U. Nestmann.
Breaking Symmetries.
Submitted to Mathematical Structures in Computer Science, 2011.
S. Mennicke (TU Braunschweig) Compositional πa ⇒ Join YR-CONCUR 2012 15 / 15