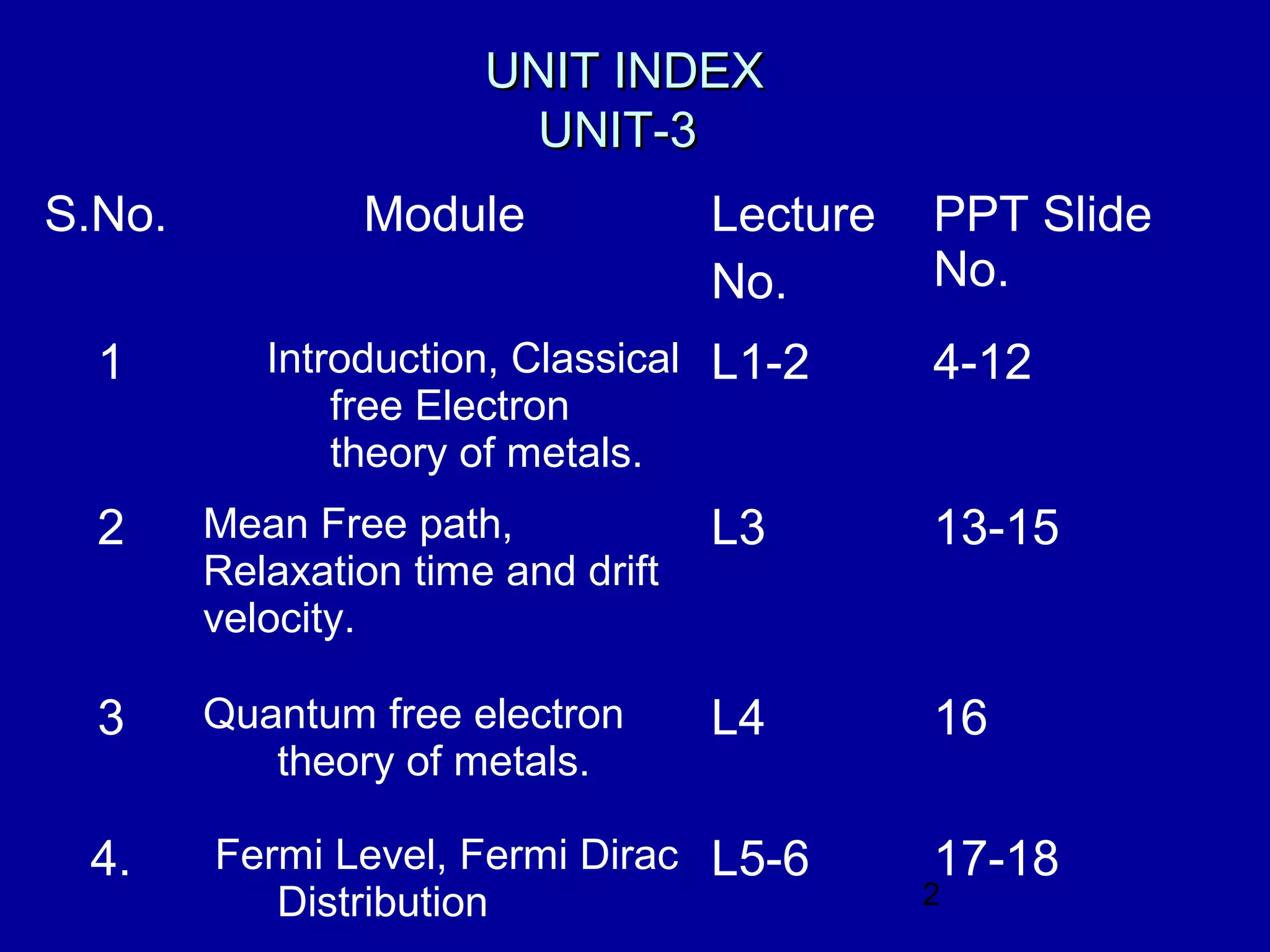
This document provides an overview of the key topics in Unit 3 of the Applied Physics course. The unit covers: 1. Classical and quantum free electron theories of metals, including the Drude-Lorentz model and Sommerfeld's quantum model. 2. Mean free path, relaxation time, and drift velocity of electrons in metals. 3. The Fermi level and Fermi-Dirac distribution of electron energies. 4. Classification of materials as insulators, semiconductors, or conductors based on their band structure and energy gaps.

1. APPLIED PHYSICS
CODE : 07A1BS05
I B.TECH
CSE, IT, ECE & EEE
UNIT-3
NO. OF SLIDES : 24
1

2. UNIT INDEX
UNIT-3
S.No. Module Lecture PPT Slide
No. No.
1 Introduction, Classical L1-2 4-12
free Electron
theory of metals.
2 Mean Free path, L3 13-15
Relaxation time and drift
velocity.
3 Quantum free electron L4 16
theory of metals.
4. Fermi Level, Fermi Dirac L5-6 17-18
Distribution 2

3. 5 Electron scattering L7 19
and resistance.
6 Classification of L8 20-23
materials
7 Effective mass of L9 24
electron
3

4. INTRODUCTION
Lecture-1
The electron theory of solids
aims to explain the structures and
properties of solids through their
electronic structure.
The electron theory of solids has
been developed in three main
stages. 4

5. (i). The classical free electron theory:
Drude and Lorentz developed this theory in
1900. According to this theory, the metals
containing free electrons obey the laws of
classical mechanics.
(ii). The Quantum free electron theory:
Sommerfeld developed this theory during
1928. According to this theory, the free
electrons obey quantum laws. 5

6. (iii). The Zone theory:
Bloch stated this theory in 1928.
According to this theory, the free
electrons move in a periodic field
provided by the lattice. This theory
is also called “Band theory of solids”.
6

7. The classical Free Electron Theory of
Metals (Drude - Lorentz theory of metals
Lecture-2
postulates :
(a). In an atom electrons revolue around the nucleus and
a metal is composed of such atoms.
(b). The valence electrons of atoms are free to move
about the whole volume of the metals like the
molecules of a perfect gas in a container. The
collection of valence electrons
from all the atoms in a given piece of metal forms
electrons gas. It is free to move throughout the
volume of the metal
7

8. (c) These free electrons move in random directions and
collide with either positive ions fixed to the lattice or
other free electrons. All the collisions are elastic i.e.,
there is no loss of energy.
(d). The movements of free electrons obey the laws of
the classical kinetic theory of gases.
(e). The electron velocities in a metal obey the classical
Maxwell – Boltzmann distribution of velocities.
8

9. (f). The electrons move in a completely
uniform potential field due to ions fixed in
the lattice.
(g). When an electric field is applied to the
metal, the free electrons are accelerated in
the direction opposite to the direction of
applied electric field.
9

10. Success of classical free electron
theory:
(1). It verifies Ohm’s law.
(2). It explains the electrical and thermal
conductivities of metals.
(3). It derives Wiedemann – Franz law. (i.e., the
relation between electrical conductivity and
thermal conductivity)
(4). It explains optical properties of metalsl.
10

11. Drawbacks of classical free electron
theory:
1. The phenomena such a photoelectric effect,
Compton effect and the black body radiation
couldn’t be explained by classical free
electron theory.
2. According to the classical free electron
theory the value of specific heat of metals is
given by 4.5Ru is the Universal gas constant
whereas the experimental value is nearly
equal to 3Ru. Also according to this theory
the value of electronic specific heat is equal
to 3/2Ru while the actual value is about 0.01Ru
11

12. 3.Electrical conductivity of semiconductor or
insulators couldn’t be explained using this
model.
4. Though K/σT is a constant (Wiedemann –
Franz Law) according to the Classical free
electron theory, it is not a constant at low
temperature.
5. Ferromagnetism couldn’t be explained by this
theory. The theoretical value of paramagnetic
susceptibility is greater than the experimental
value. 12

13. Mean free path Lecture-3
The average distance traveled by an electron
between two successive collisions inside a
metal in the presence of applied field is known
as mean free path.
13

14. Relaxation Time
The time taken by the electron to
reach equilibrium position from
its disturbed position in the
presence of an electric field is
called relaxation time.
14

15. Drift velocity
• In the presence of electric field, in
addition to random velocity there is an
additional net velocity associated with
electrons called drift velocity.
• Due to drift velocity, the electrons with
negative charge move opposie to the
field direction.
15

16. Quantum free electron Theory
Lecture-4
• According to quantum theory of free
electrons energy of a free electron is given
by
• En = n2h2/8mL2
• According to quantum theory of free
electrons the electrical conductivity is given
by
• σ = ne2T/m
16

17. Fermi Level
Lecture-5
• “The highest energy level that can be
occupied at 0K” is called Fermi level.
• At 0K, when the metal is not under the
influence of an external field, all the levels
above the Fermi level are empty, those
lying below Fermi level are completely
filled.
• Fermi energy is the energy state at which the
probability of electron occupation is ½ at any
temperature above 0k. 17

18. Fermi-Dirac statistics
Lecture-6
According to Fermi Dirac statistics, the
probability of electron occupation an
energy level E is given by
F(E) = 1/ 1+exp (E-EF/kT)
18

19. Electrical Resistivity Lecture-7
• The main factors affecting the electrical
conductivity of solids are i) temperature
and ii) defects (i.e. impurities).
• According to Matthiesens’s rule, the
resistivity of a solid is given by
ρpure= ρpure+ ρimpurity
where ρpure is temperature dependent
resistivity due to thermal vibrations of the
lattice and ρimpurity is resistivity due to
19

20. CLASSIFICATION OF MATERIALS
Lecture-8
• Based on ‘band theory’, solids
can be classified into three
categories, namely,
1. insulators,
2. semiconductors &
3. conductors.
20

21. INSULATORS
• Bad conductors of electricity
• Conduction band is empty and
valence band is full, and these band
are separated by a large forbidden
energy gap.
• The best example is Diamond with
Eg=7ev.
21

22. SEMI CONDUCTORS
• Forbidden gap is less
• Conduction band an d valence band
are partially filled at room
temperature.
• Conductivity increases with
temperature as more and more
electrons cross over the small energy
gap.
22
• Examples Si(1.2ev) & Ge(0.7ev)

23. CONDUCTORS
• Conduction and valence bands are
overlapped
• Abundant free electrons already exist in
the conduction band at room temperature
hence conductivity is high.
• The resistively increases with
temperature as the mobility of already
existing electrons will be reduced due to
collisions.
• Metals are best examples.
23

24. EFFECTIVE MASS
Lecture-9
• Def : When an electron in a periodic
potential of lattice is accelerated by
an electric field or magnetic field, then
the mass of the electron is called
effective mass.
• It is denoted by m*
m* = ћ2/(d2E/dk2)
24