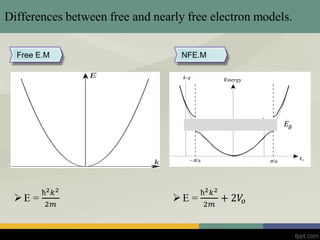
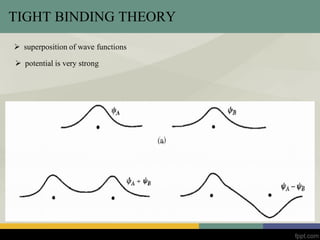
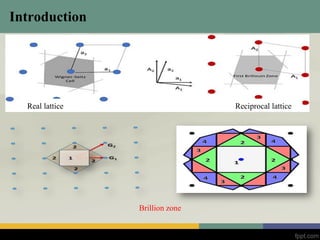
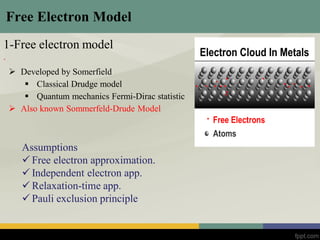
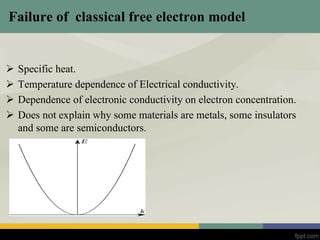
This document discusses band theory and several models used to describe electron behavior in solids, including the free electron model, nearly free electron model, and tight binding model. It provides an overview of each model, including their assumptions and how they describe properties like electron energy and band gaps. The free electron model treats electrons as independent particles but fails to explain material properties. The nearly free electron model incorporates a periodic potential and allows electron wavefunctions and energy bands to be described. The tight binding model uses a superposition of atomic orbitals to approximate electron wavefunctions in solids where potential is strong.

1. Prepared by :
Ballen Zangana

2. Outline
Company Logo
Introduction
Models
What is band theory ?
Free electron model
Nearly free electron model
Tight binding model
p to n-type transition with wide blue shift
optical band gap of spray synthesized Cd
doped CuO thin films for optoelectronic
device applications

3. Introduction
Brillion zone
Reciprocal latticeReal lattice

4. What is Band Theory ?
Free electron model1
Green's function methods & the ab initio GW app.
Dynamical mean field theory
DFT Theory
4
2
3
6
5
7
Tight binding theory
Nearly free electron model
KKR (Korringa and Kohn and Rostocker) model
 The calculation of the allowed electron states in a solid is referred
to as band theory or band structure theory.
 Models

5. Free Electron Model
1-Free electron model
.
 Developed by Somerfield
 Classical Drudge model
 Quantum mechanics Fermi-Dirac statistic
 Also known Sommerfeld-Drude Model
Assumptions
 Free electron approximation.
 Independent electron app.
 Relaxation-time app.
 Pauli exclusion principle

6. Failure of classical free electron model
 Specific heat.
 Temperature dependence of Electrical conductivity.
 Dependence of electronic conductivity on electron concentration.
 Does not explain why some materials are metals, some insulators
and some are semiconductors.

7. Nearly free electron approximation
 Quantum mechanics model
 Weak potential limit
 In nearly free electron consider electron in solid against periodic
potential.(V=Vo).
a
L
𝑘 =
2𝜋
𝐿
𝑘 =
2𝜋
𝑎
L

8. Wave function for electron in NFE approximation
−
ħ2
2𝑚
𝜕2
𝜕2 𝑥
+ v(x)) Ψ(x)=E Ψ(x)
Ψ(x)≈u(x)
Ψ(x)≈u(x) 𝑒 𝑖(𝑘𝑥−𝑤𝑡)
u(x)= u(x+a)= u(x+2a)=………….
u(x)= u(x+a)
Ψ(x+a) 𝑒−𝑖(𝑘𝑥+𝑘𝑎−𝑤𝑡)
= Ψ(x) 𝑒 𝑖(𝑘𝑥−𝑤𝑡)
Ψ(x+a)= 𝑒 𝑖(𝑘𝑎)
Ψ(x)

9. ka= ±m π m=0
m=1,2,3,………
Some special things happened when phase : 𝑒 𝑖(𝑘𝑎)
=1
k= ±
𝜋
𝑎
, ±2
𝜋
𝑎
, ±3
𝜋
𝑎
,…….
Consider a set of waves with± k-pairs, e.g. k= ±
𝜋
𝑎
k= +π/a moves
k= -π/a moves

10. This defines a pair of waves moving right and left.
Two trivial ways to superpose these waves are:
𝜳+
≈ 𝒆𝒊(𝒌𝒙)
+𝒆−𝒊(𝒌𝒙)
𝜳−
≈ 𝒆𝒊(𝒌𝒙)
-𝒆−𝒊(𝒌𝒙)
𝜳+
≈2cos(kx) 𝜳−
≈2isin(kx)
|𝜳+
| 𝟐
≈4𝒄𝒐𝒔 𝟐
(kx) |𝜳−
| 𝟐
≈4𝒔𝒊𝒏 𝟐
(kx)

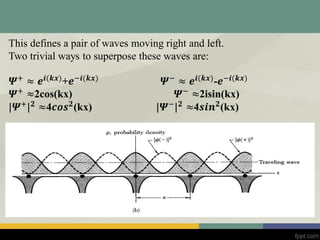
11. Energy versus wave vector
 Can draw E(k) in three ways.
𝐸𝑔 = 𝑑𝑥
1
0
𝑈 𝑥 [Ѱ(+)]2
- [Ѱ(-)]2
𝐸𝑔= 2 𝑑𝑥 𝑈 cos
2𝜋
𝑎
(𝑐𝑜𝑠2 𝜋𝑥
𝑎
- 𝑠𝑖𝑛2 𝜋𝑥
𝑎
)

12. Differences between free and nearly free electron models.
E =
ħ2 𝑘2
2𝑚
E =
ħ2 𝑘2
2𝑚
+ 2𝑉𝑜
Free E.M NFE.M
𝐸 𝑔

13. TIGHT BINDING THEORY
 superposition of wave functions
 potential is very strong

14.  An approximate wave function for one electron in the whole crystal
by taking
Ψ𝑘(r)= 𝑗 𝐶 𝑘𝑗 φ(r-𝑟𝑗)

15. 1-C.kittle, 2005, Introduction to Solid state Physics, Johnwily &sons
, Inc,USA.
2-J.D.Ptterson, B.C .Bailey , 2007, solid-state physics introduction to
the theory , springer, USA.
3-R.G.Chambers, 1990, Electrons in metals and Semiconductor ,
Champan and Hall , London.
4-Uichiro Miztani , 2003, Introduction to the Electron Theory of
Metals, Cambridge University press , USA.
5-M.Ali Omer, 1975, Elementary Solid State Physics: Principle and
Applications, Addison-wesley , Cananda .
6-J.J.Quinn, kuyurg-sooyi , 2009, Solid State Physics Principle And
Modern Applications, springer, USA.
References

16. 7-M.Hilke, 2006, Solid State Physics, Lecture Notes, Mc Gill
University, 25 October 2006.
8-J.Gladh, 2006,` Scanning Tunneling Microscopy and Low-
Energy Electron Diffraction Studies of Quantum Wires On
Si(332)`, Mc Thesis , Karlstads University, Karlstad.
9-H.Ibach, H.Lüth , 2009, Solid-State Physics An Introduction
to Principle of Materials Science, Springer, London.
10-E.Scerri, 1995,`The exclusion Principle`, Chemistry and
Hidden Variables`, Center for Philosophy of Natural and Social
sciences.
11-G.Zengin et al, 2009, ` Evaluation of students’
understanding of Pauli’s exclusion principle`, Elsevier.
12-M.Roy, 2015,The Tight Binding Method, Lecture Notes,
May.7 2015.