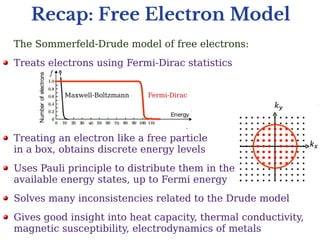
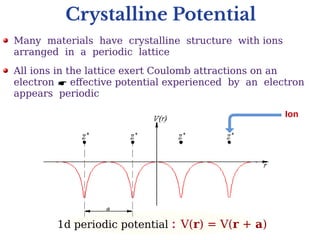
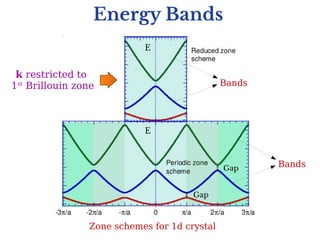
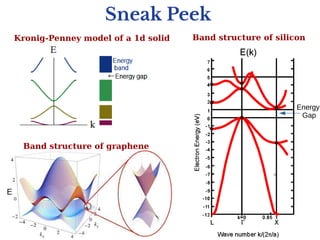
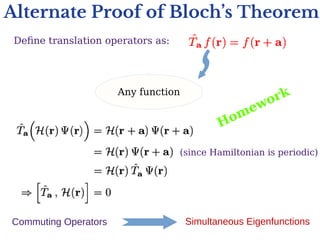
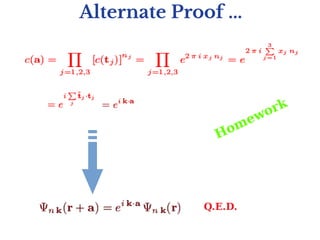
Electronic band structures in crystals can be understood using Bloch's theorem. Bloch's theorem states that the eigenstates of electrons moving in a periodic potential can be written as a plane wave multiplied by a periodic function. This leads to the formation of allowed energy bands separated by forbidden band gaps. The energy bands arise because the electron momentum is restricted to the first Brillouin zone of the crystal lattice. Bloch's theorem provides insights into the distinction between metals, semiconductors and insulators by explaining whether the Fermi energy lies in an allowed band or forbidden band gap.

1. Electronic Band Structures:
Electronic Band Structures:
Bloch's Theorem
Bloch's Theorem
Ipsita Mandal

2. References
Introduction to Solid State Physics
by Charles Kittel, Chapter 7
Solid-State Physics: An Introduction to Principles of
Materials Science
by Harald & Ibach, Harald, Hans Lüth, Chapter 7
Solid State Physics
by Neil W. Ashcroft & N. David Mermin, Chapter 8

3. Recap: Free Electron Model
The Sommerfeld-Drude model of free electrons:
Treats electrons using Fermi-Dirac statistics
Treating an electron like a free particle
in a box, obtains discrete energy levels
Uses Pauli principle to distribute them in the
available energy states, up to Fermi energy
Solves many inconsistencies related to the Drude model
Gives good insight into heat capacity, thermal conductivity,
magnetic susceptibility, electrodynamics of metals
Fermi-Dirac
Maxwell-Boltzmann

4. Drawbacks of Free Electron Model
It fails in explaining:
Distinction between metals, semimetals, semiconductors,
insulators
Occurrence of positive values of Hall coefficient
Relation of conduction electrons in metals to valence
electrons of free atoms
Many transport properties, particularly magnetotransport

5. Band Structures
Many of these deficiencies solved by taking into account
periodic lattice ☛ we will see:
Electrons in crystals are arranged in energy bands separated
by forbidden regions of energy for which no wavelike
electron orbitals exist
Metals: Fermi energy (EF
) in band; Insulators: EF
in gap

6. Crystalline Potential
Many materials have crystalline structure with ions
arranged in a periodic lattice
All ions in the lattice exert Coulomb attractions on an
electron ☛ effective potential experienced by an electron
appears periodic
1d periodic potential : V(r) = V(r + a)
Ion

7. Effect of Periodic Potential
Schrodinger equation for single electron
Periodic
Generic position
vector on a
Bravais lattice

8. Bloch’s Theorem
Eigenstates of periodic Hamiltonian can be chosen as:
“Bloch electrons” ☛ electrons with wavefunctions obeying
Bloch’s Theorem
Plane wave
Periodic in a
Consequence
of
discrete
translation
sym
m
etry

9. Periodic Boundary Conditions
Generalize Born-von Karman periodic boundary conditions
(p. b. c.) of Sommerfeld model:
Assumption: Bulk properties not affected by choice of
boundary conditions
The generic Bravais lattice has N primitive cells with
N1 t1
N2 t2
N3 t3

10. Plane Waves Obeying P.B.C.
For plane waves obeying p.b.c.:
Expressing
gives
Bloch wave vector

11. Proof of Bloch’s Theorem
We can expand any function obeying p.b.c in the complete
set of plane waves obeying p. b. c.:
For periodic potential:
is a reciprocal lattice vector

12. Proof of Bloch’s Theorem ...
Fourier transformation
Q.E.D.

13. Emergence of Energy Bands
Due to lattice periodicity, we can regard this as an Hermitian
eigenvalue problem restricted to a primitive cell
Fixed volume ☛ an infinite family of solutions with discretely
spaced eigenvalues (just like free particle in a box), labelled
by “band index” n

14. Emergence of Energy Bands ...
Eigensolutions are continuous functions of the parameter k
It then follows that:
Each band index n corresponds to a unique periodic solution
periodic + continuous ☛ its value is bounded
☛ allowed electronic levels form a band

15. Energy Bands
E
E
Gap
Gap
Zone schemes for 1d crystal
Bands
Bands
k restricted to
1st
Brillouin zone

16. Sneak Peek
Band structure of silicon
Kronig-Penney model of a 1d solid
Energy
Gap
Band structure of graphene
E

17. Alternate Proof of Bloch’s Theorem
Define translation operators as:
Any function
Simultaneous Eigenfunctions
Commuting Operators
(since Hamiltonian is periodic)
Homework

18. Alternate Proof ...
We choose eigenstates of Hamiltonian as simultaneous eigenstates of
lattice translation operators:
Eigenvalues
Homework

19. Alternate Proof ...
We found the eigenvalues obeying:
For an infinite lattice with discrete translational symmetry (a) :
Translation operator is
unitary ☛ its
eigenvalues must be
phases
Homework

20. Alternate Proof ...
Q.E.D.
Homework
Q.E.D.

21. Insights from Bloch’s Theorem
Concept of band structures can be understood as we observe
emergence of allowed & forbidden energy ranges
Bloch’s theorem guarantees that any single-electron
eigenstate = (plane wave) ⨯ (some periodic function)
When electrons move in a periodic potential, gaps arise in
their dispersion relation at Brillouin zone boundaries: we will
see this next by solving the simple Kronig–Penney model