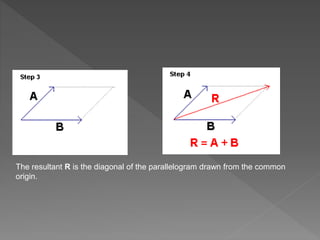
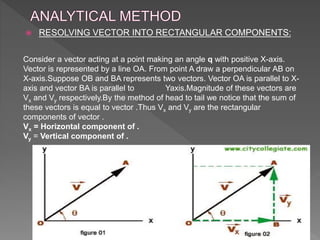
This document discusses physical quantities and vectors. It defines two types of physical quantities: scalar quantities which have only magnitude, and vector quantities which have both magnitude and direction. Examples of each are given. Vector quantities are represented by magnitude and direction. The document then discusses methods for adding and subtracting vectors graphically using head-to-tail and parallelogram methods. It also covers resolving vectors into rectangular components, finding the magnitude and direction of vectors, dot products of vectors which yield scalar quantities, and cross products of vectors which yield vector quantities. Examples of applying these vector concepts are provided.

2.  The observable and measurable quantities
are called physical quantities.
TYPES OF PHYSICAL QUANTITIES:
 Scalar quantities
 Vector quantities

3. Those quantities which have magnitude without
directions.
EXAMPLES:
a. Mass
b. Speed
c. work
d. Energy
e. temperature

4. Physical quantities those are represented by a
number (magnitude) with appropriate unit and a
particular direction are called as vector.
Examples:
 Displacement.
 Force.
 Momentum.
Torque.

5.  Such vector, whose magnitude and
direction is same as that of magnitude and
directions of a given position vector, is
called equal to the position vector”.

6.  Such vectors whose magnitude is zero and
which has no direction or which may have
all directions is called null vector.

7.  A process in which two or more vectors are
combine to get a resultant vector is called
addition of vector.

8.  Similarly orientated vectors can be
subtracted the same manner.

9.  GRAPHICAL METHOD
 ANALYTICAL METHOD
 GRAPHICAL METHOD:
a. HEAD TO TAIL RULE
b. PARALLELOGRAM METHOD

10.  Two vectors A and B are added by drawing the arrows which
represent the vectors in such a way that the initial point of B is on the
terminal point of A. The resultant R=A+B+C, is the vector from the
initial point of A to the terminal point of C.
R = A +B+C

11. In the parallelogram method for vector addition, the vectors are
translated, (i.e., moved) to a common origin and the parallelogram
constructed as follows:

12. The resultant R is the diagonal of the parallelogram drawn from the common
origin.

13.  The process of splitting a vector into various parts or components is called
"RESOLUTION OF VECTOR" These parts of a vector may act in different
directions and are called "components of vector".
 We can resolve a vector into a number of components .Generally there are
three components of vector viz.
Component along X-axis called x-component
Component along Y-axis called Y-component
Component along Z-axis called Z-component
 Here we will discuss only two components x-component & Y-component
which are perpendicular to each other.These components are called
rectangular components of vector.

14.  RESOLVING VECTOR INTO RECTANGULAR COMPONENTS:
Consider a vector acting at a point making an angle q with positive X-axis.
Vector is represented by a line OA. From point A draw a perpendicular AB on
X-axis.Suppose OB and BA represents two vectors. Vector OA is parallel to X-
axis and vector BA is parallel to Yaxis.Magnitude of these vectors are
Vx and Vy respectively.By the method of head to tail we notice that the sum of
these vectors is equal to vector .Thus Vx and Vy are the rectangular
components of vector .
Vx = Horizontal component of .
Vy = Vertical component of .

15.  MAGNITUDE OF HORIZONTAL COMPONENT
Consider right angled triangle DOAB
Consider right angled triangle DOAB
• MAGNITUDE OF VERTICAL COMPONENT

16.  MAGNITUDE OF VECTOR:
The magnitude of A, |A|, can be calculated from the components, using the
Theorem of Pythagoras:
 DIRECTION OF VECTOR:
 The direction can be calculated using trignometric ratio.

17.  If the product of two vector is a scalar quantity is called scalar or
dot product.
 The dot product of two vector making angle b/w them is given by;
I. A . B =ABCosO
II. A .B =A(BCosO)
EXAMPLE:
W=FS OR P=FV
The product of two vector force and displacement is work which is scalar quantity.
PROPERTIES:
1) A . B=B . A
2) A . B = O if O = 90
3) A . B = AB(max) if O =O
4) i . i = j . j = k . k = 1
5) i . j = j . k = k . i = O

18. Q: Find work If S = 3i + 2j – 5k and F =2i – j - k
ANS:
W = FS
W = (2i – j – k ) . (3i + 2j -5k )
W =6 (i . i) -2 (j . J) +5 (k . K)
W = 6 (1) -2 (1) + 5 (k . K)
W = 6 – 2 + 5
W = 9 units

19.  If the product of two vector is a vector quantity product is called
vector or cross product.
 MATHEMATICALLY,
A B = AB SinO n
Where ABSinO is magnitude of A B and n is a unit vector that give direction of
A B and direction perpedicular to both A and B which can be find by R . H . RULE.
PROPERTIES:
1) A B = B A
2) A B = AB (max) when O=90
3) A B = O if O =O
4) i i = j j = k k = O
5) i j = k , j k = i , k i = j

20.  EXAMPLE:
= F S
Force and displacement is a vector quantity and its result TORQUE is also a vector.
QUESTION
Q: Find cross product of A & B if A =2i – 3j – k , B = i +4j – 2k ?
ANS.