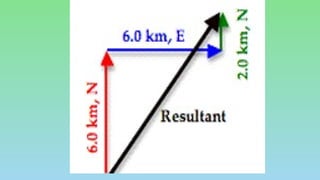
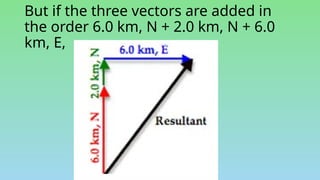
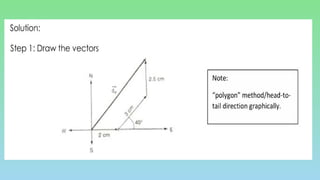
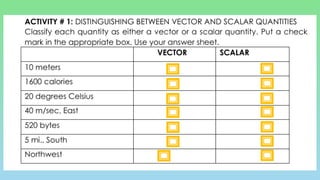
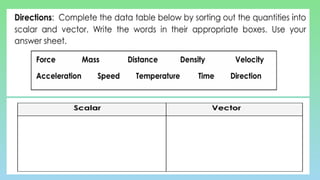
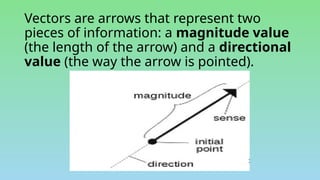
This document explains the differences between scalar and vector quantities, highlighting that scalars have only magnitude while vectors have both magnitude and direction. It provides methods for adding vectors, including graphical techniques and algebraic methods, with examples illustrating these concepts. The document emphasizes the importance of understanding vectors in terms of displacement and direction in physical movements.

1. UNDERSTANDIN
G VECTORS

2. Objectives:
By the end of this lesson, you will be
able to:
Differentiate a Vector from a Scalar
quantity
• Demonstrate how to add vectors
graphically and by component method.
Show patience in finding the resultant
vector.

4. Identifying Scalars and Vectors
Physical quantities can be specified
completely by giving a single number
and the appropriate unit.
1. a TV program lasts 40 min
2. the distance between two posts is
50 m

5. A physical quantity that can be specified
completely in this manner is called a scalar
quantity. A scalar is a quantity that is completely
specified by its magnitude and has no direction.
Example
mass, volume, distance,
temperature, energy, and time.

6. A vector is a quantity that
includes both a magnitude and
a direction.
Example
velocity, acceleration, and
force.

7. Vectors are arrows that represent two
pieces of information: a magnitude value
(the length of the arrow) and a directional
value (the way the arrow is pointed).

8. In terms of movement, the
information contained in the vector
is the distance traveled and the
direction traveled. Vectors give us a
graphical method to calculate the
sum of several simultaneous
movements.

9. We draw a vector from the initial point or
origin (called the “tail” of a vector) to the
end or terminal point (called the “head” of a
vector), marked by an arrowhead.
Magnitude is the length of a vector and is
always a positive scalar quantity.

10. To sum it up, a vector
quantity has a direction and a
magnitude, while a scalar has
only a magnitude. You can tell
if a quantity is a vector by
whether it has a direction
associated with it.

11. Adding Vectors Using Pythagorean theorem Consider
the following examples below.
Example 1: Blog walks 35 m East, rests for 20 s and
then walks 25 m East.
What is Blog’s overall displacement?
Solve graphically by drawing a scale diagram.
1 cm = 10 m Place vectors head to tail and measure
the resultant vector. Solve algebraically by adding the
two vectors acting in the same direction. R= 35 m East
+ 25 m East = 60 m East

12. Example 2: Blog walks 35 m [E], rests for
20 s and then walks 25 m [W]. What is
Blog’s overall displacement?
Using algebraic solution, we can still add the two
vectors acting in opposite direction. We can only do
this because the vectors are parallel. We must make
one vector negative to indicate opposite direction.

13. R= 35 m East + 25 m West
= 35 m East + – 25 m East
= 10 m East

14. If the vectors are acting at a certain angle,
the resultant vector is determine by:
1. Graphical method
a. Parallelogram
b. Polygon
2. Analytical or Mathematical method
a. Trigonometry
b. Component

15. Example 3: Eric leaves the base camp
and hikes 11 km, north and then hikes
11 km east. Determine Eric's resulting
displacement.

16. Example:
A student drives his car 6.0 km,
North before making a right-hand
turn and driving 6.0 km to the East.
Finally, the student makes a left-
hand turn and travels another 2.0
km to the north. What is the
magnitude of the overall

18. But if the three vectors are added in
the order 6.0 km, N + 2.0 km, N + 6.0
km, E,

20. Vector Addition: Component Method
When vectors to be added are not
perpendicular, the method of addition
by components described below can
be used. To add two or more vectors
A, B, C, … by the component method,
follow this procedure:

22. Sample problem: An ant crawls on a
tabletop. It moves 2 cm East, turns 3 cm
40O North of East and finally moves 2.5 cm
North. What is the ant’s total displacement?