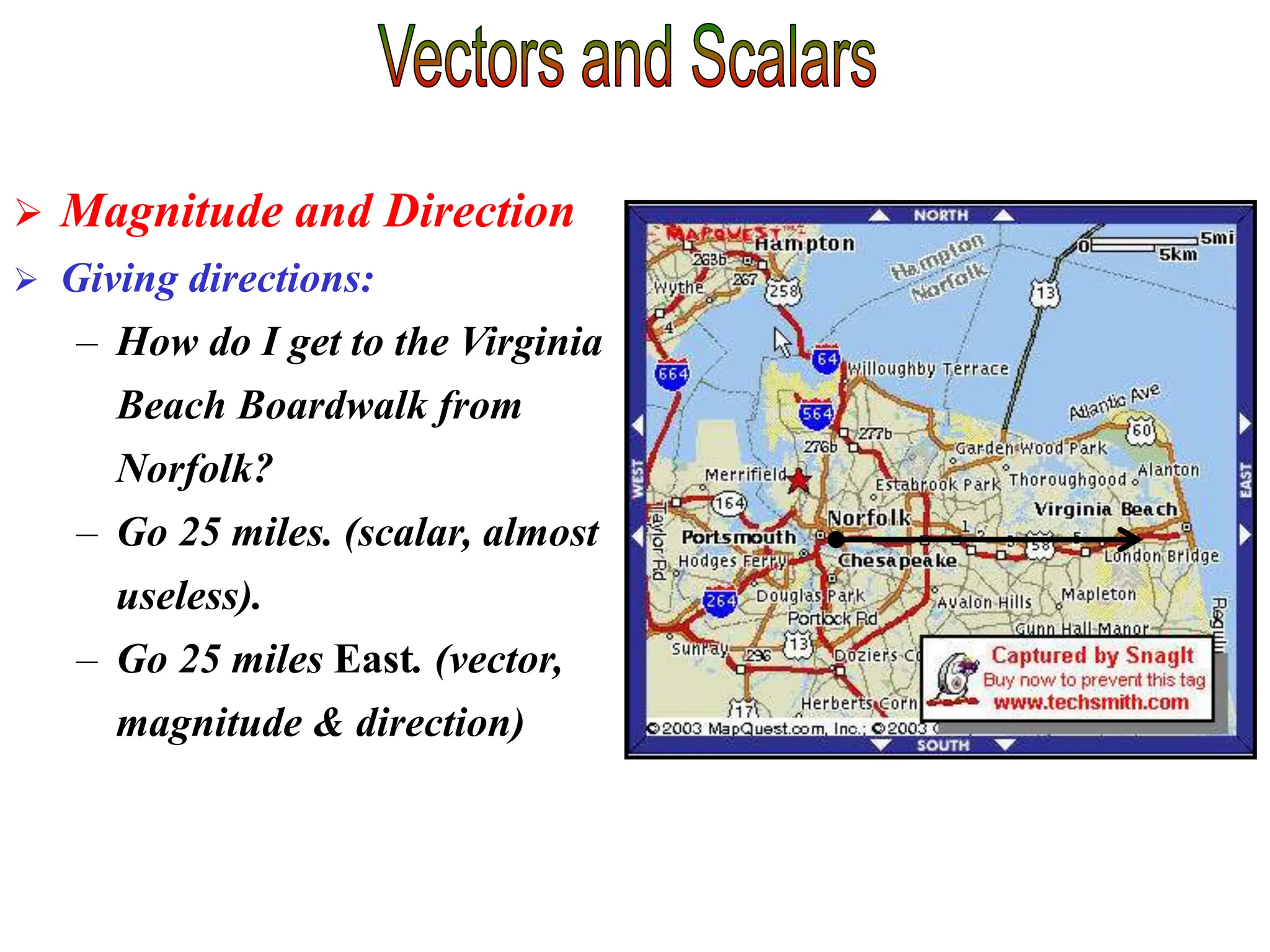
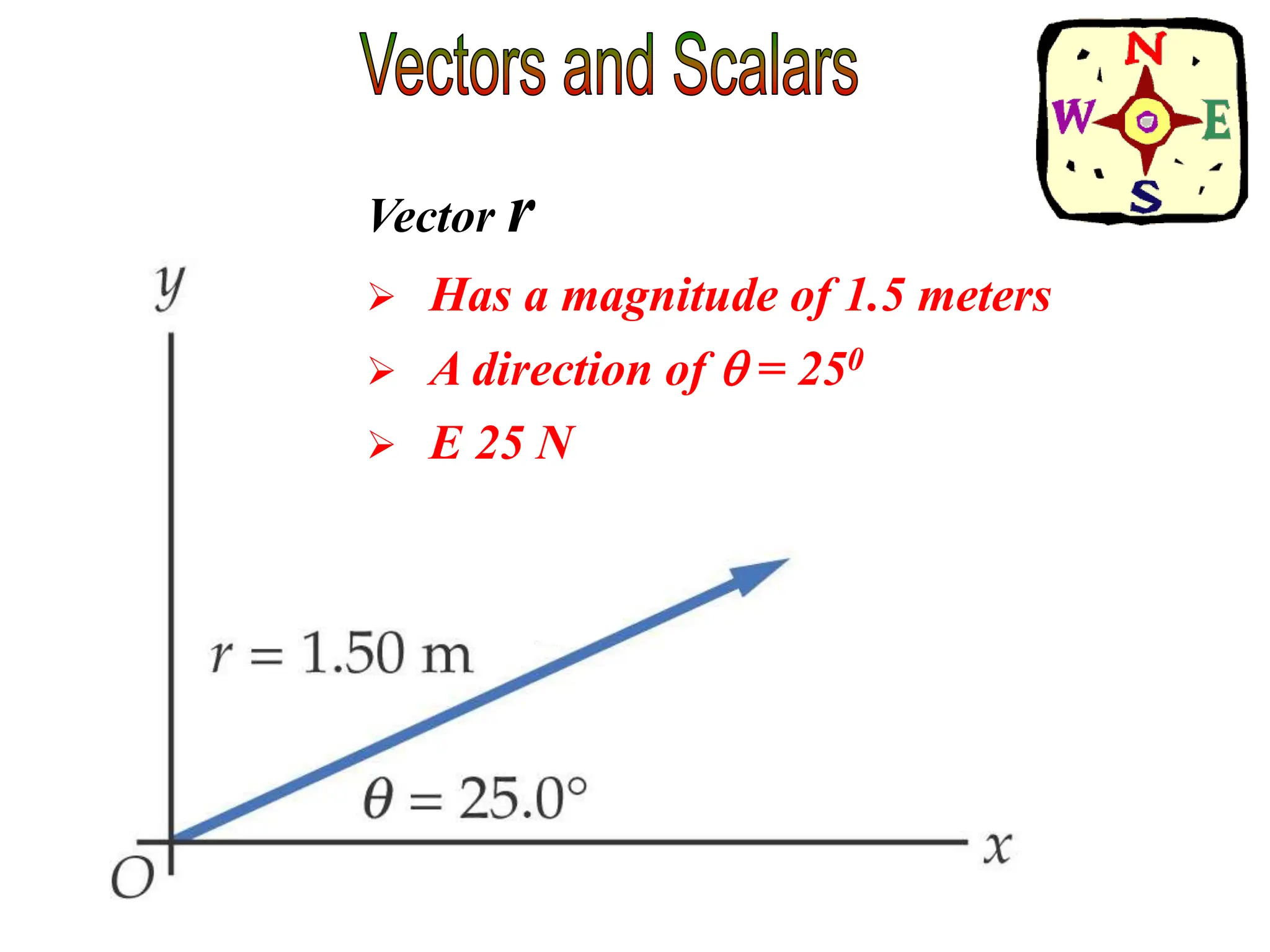
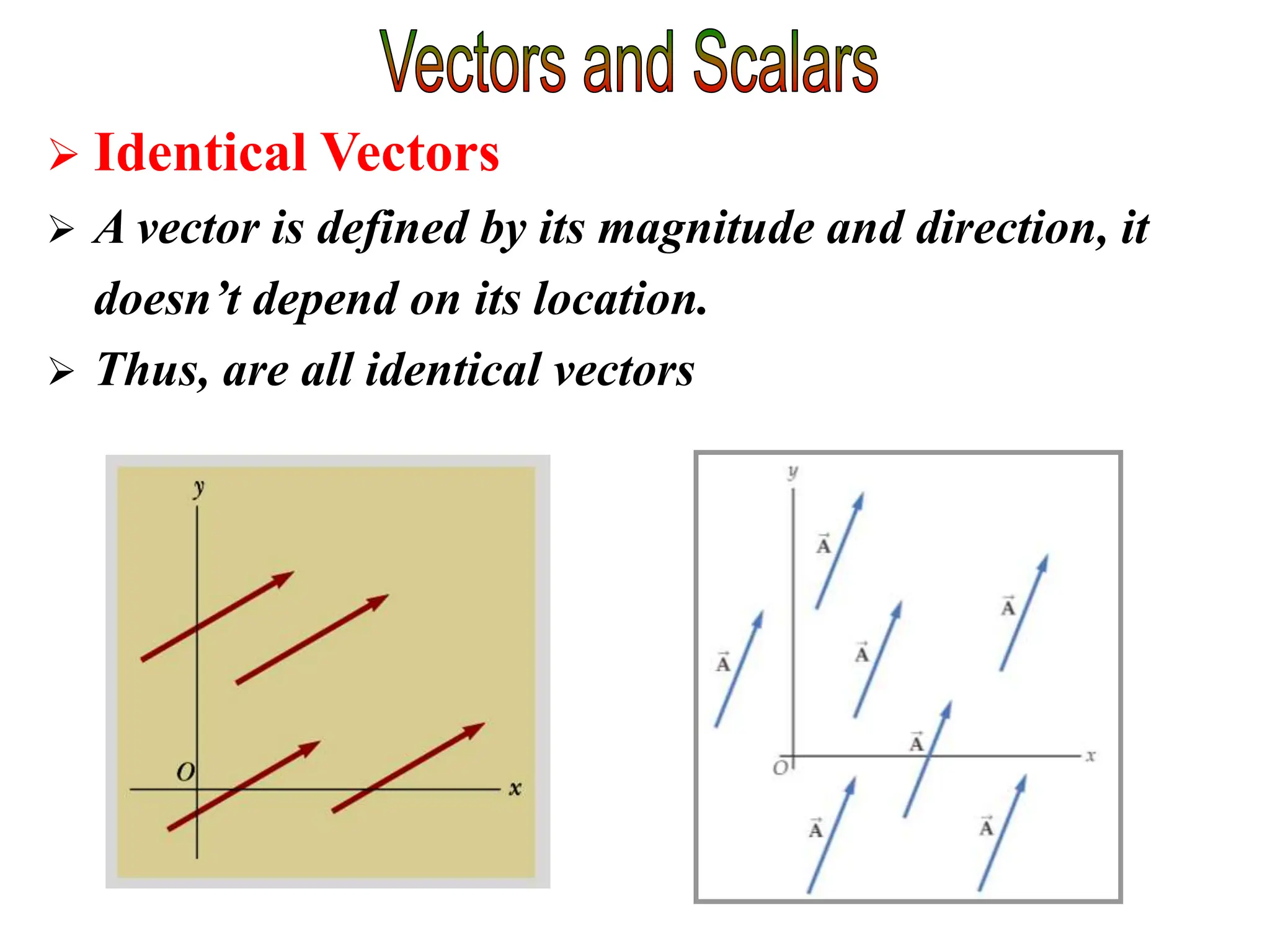
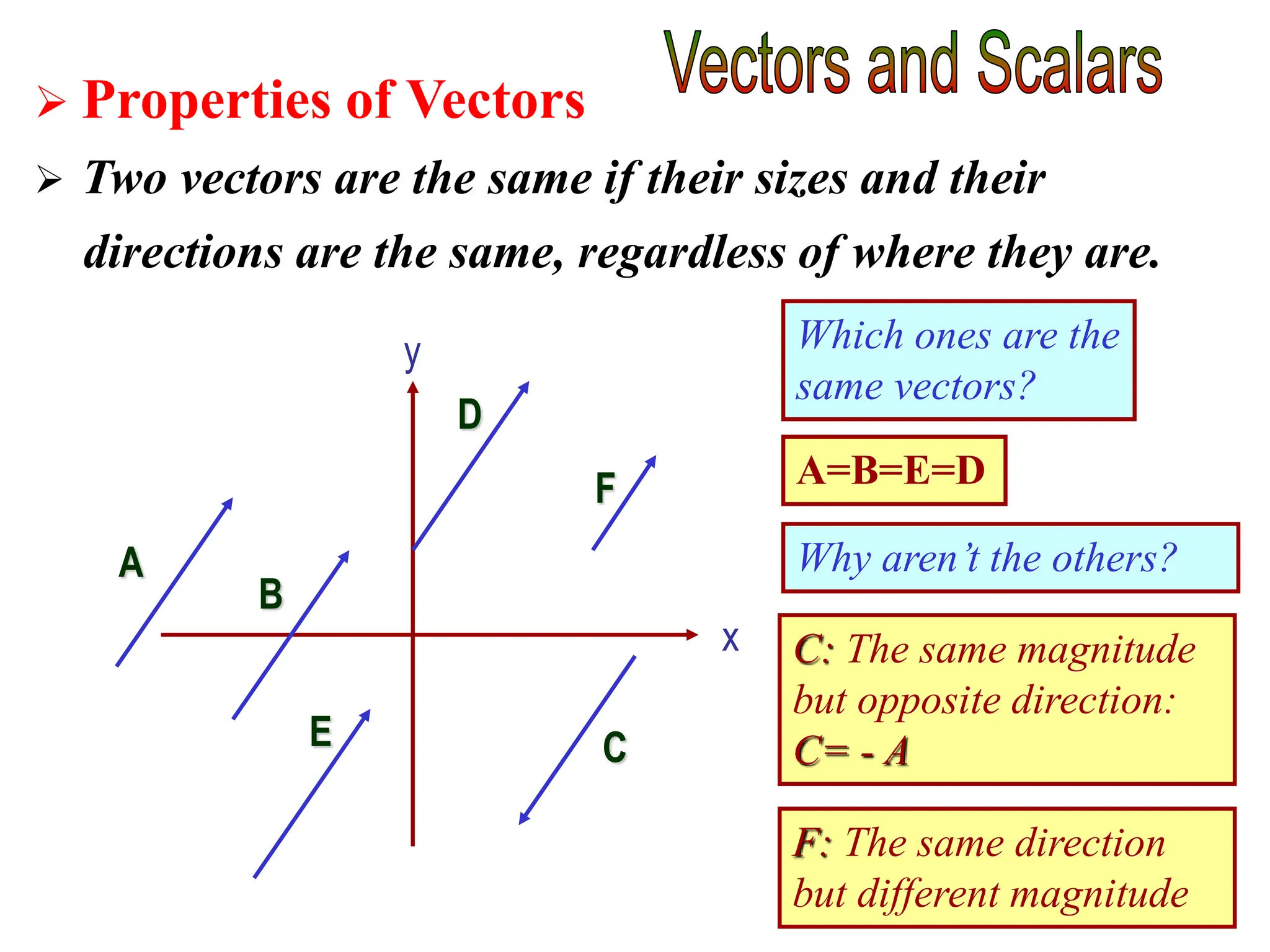
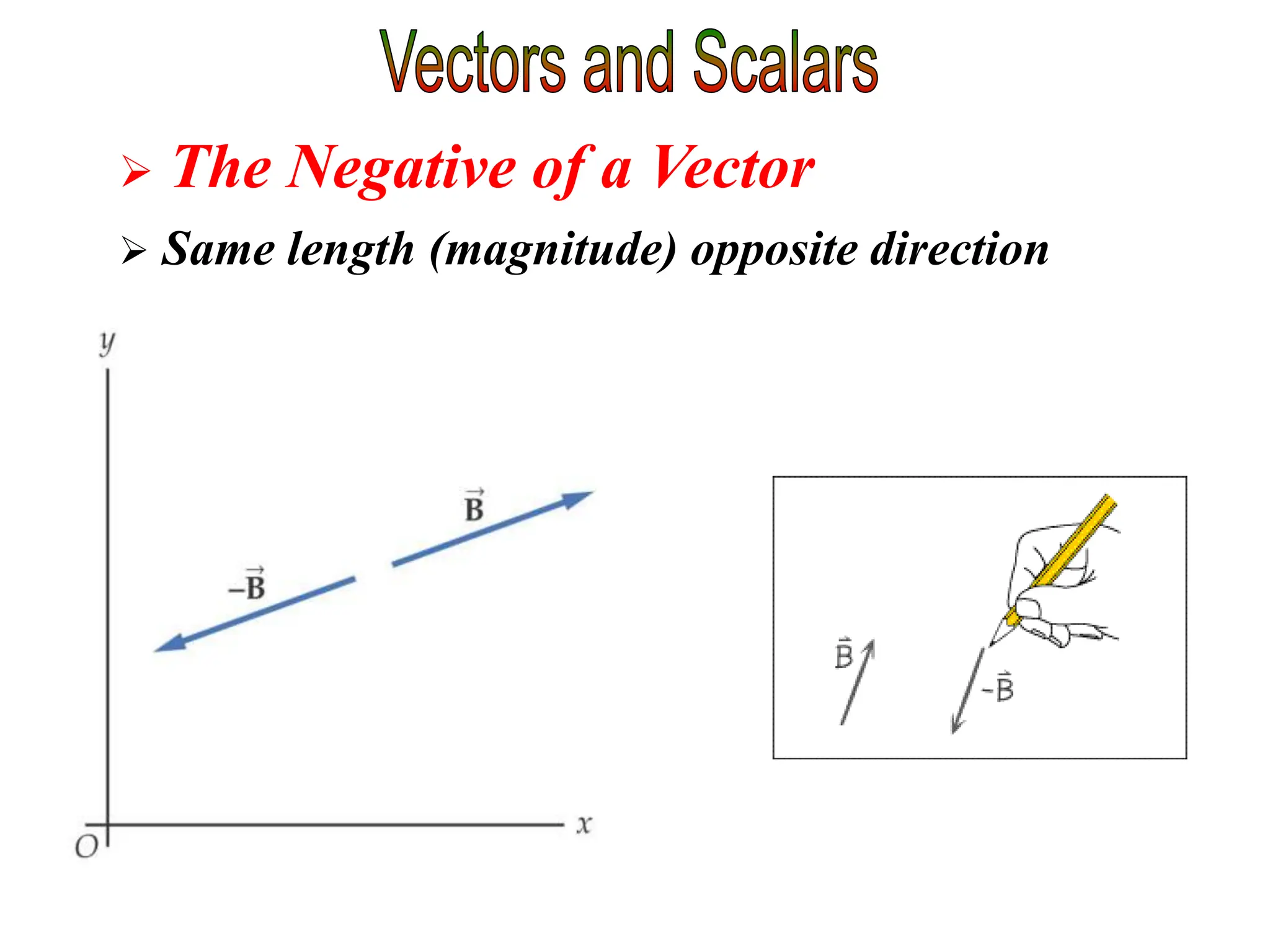
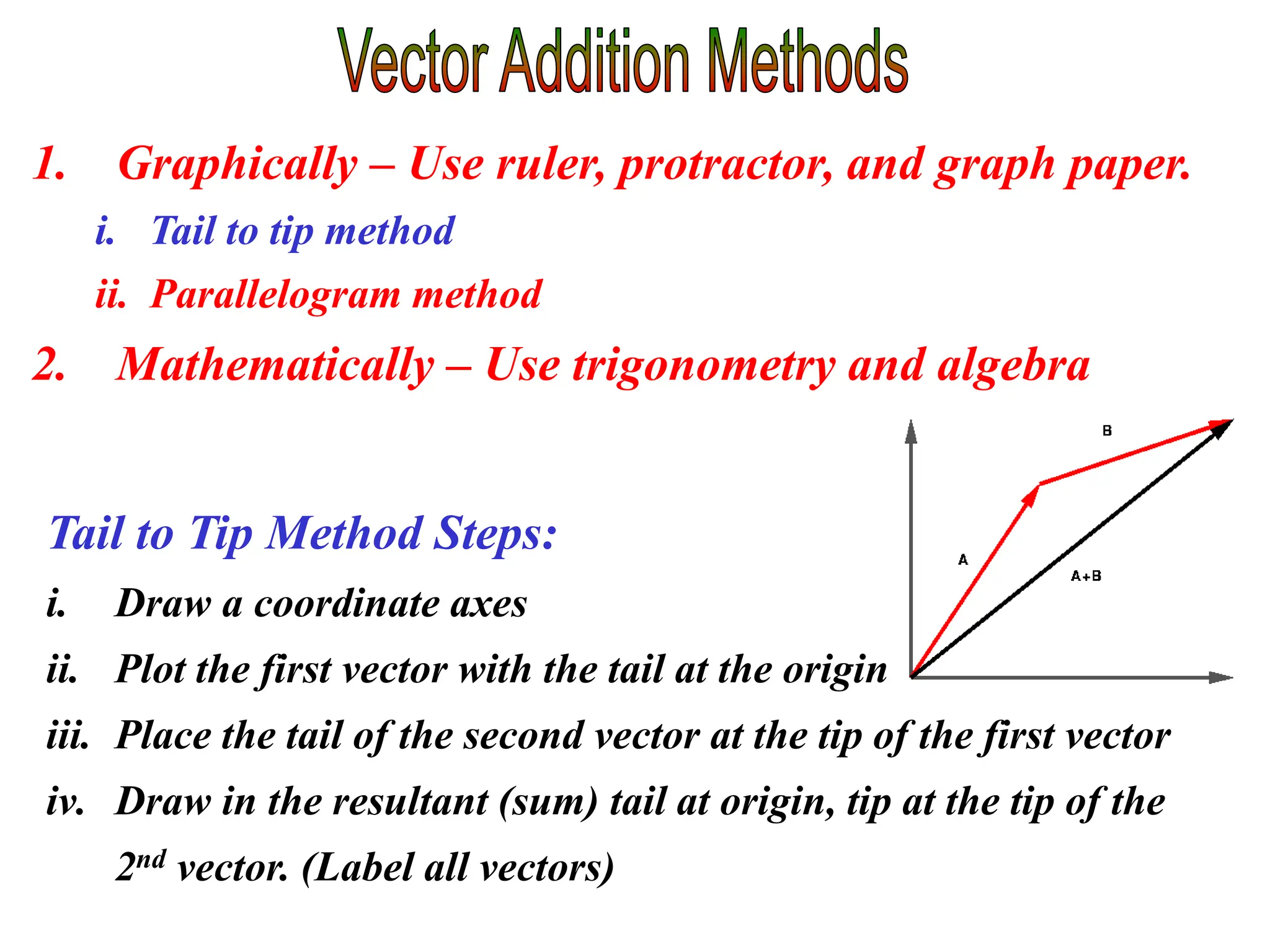
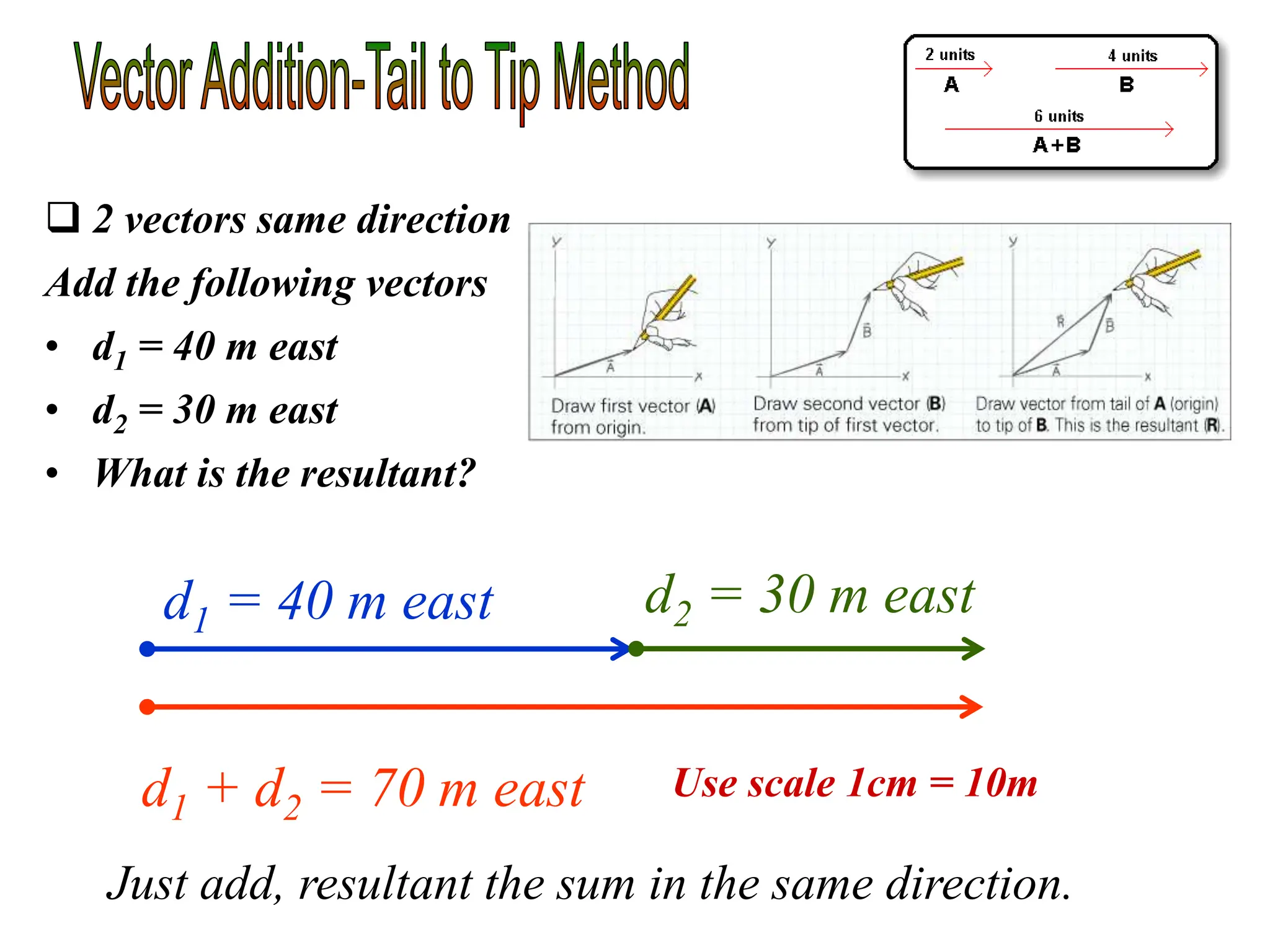
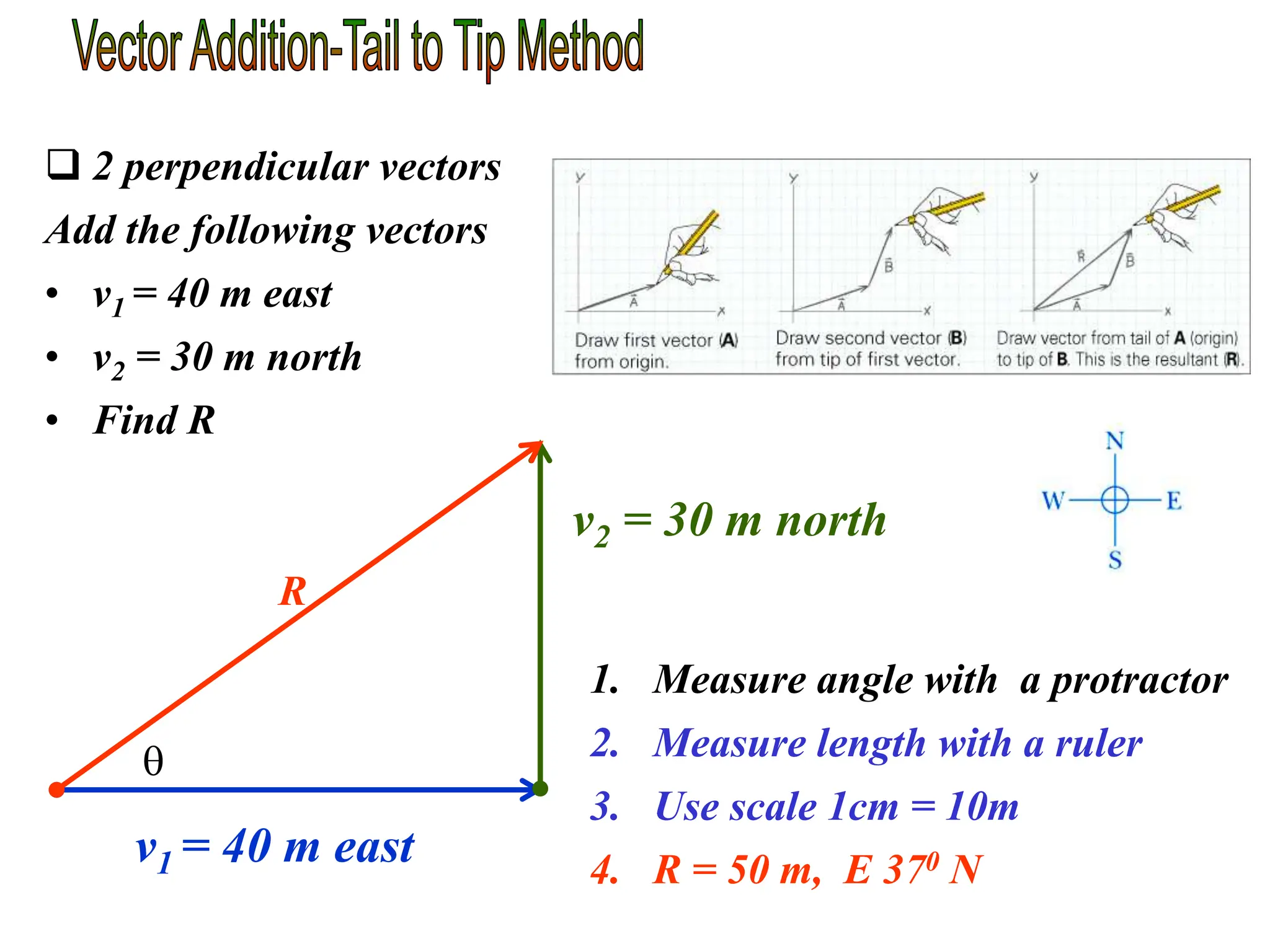
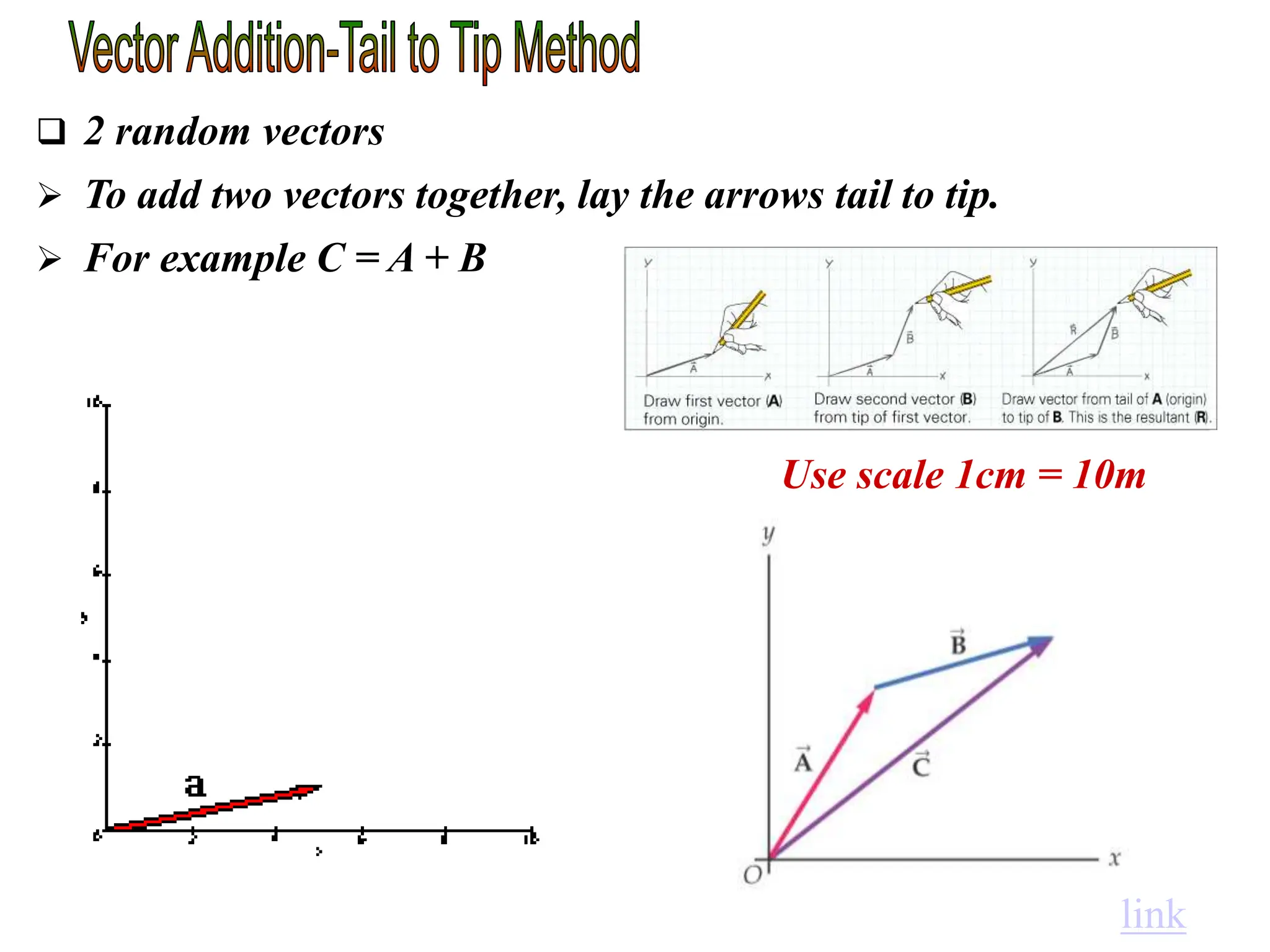
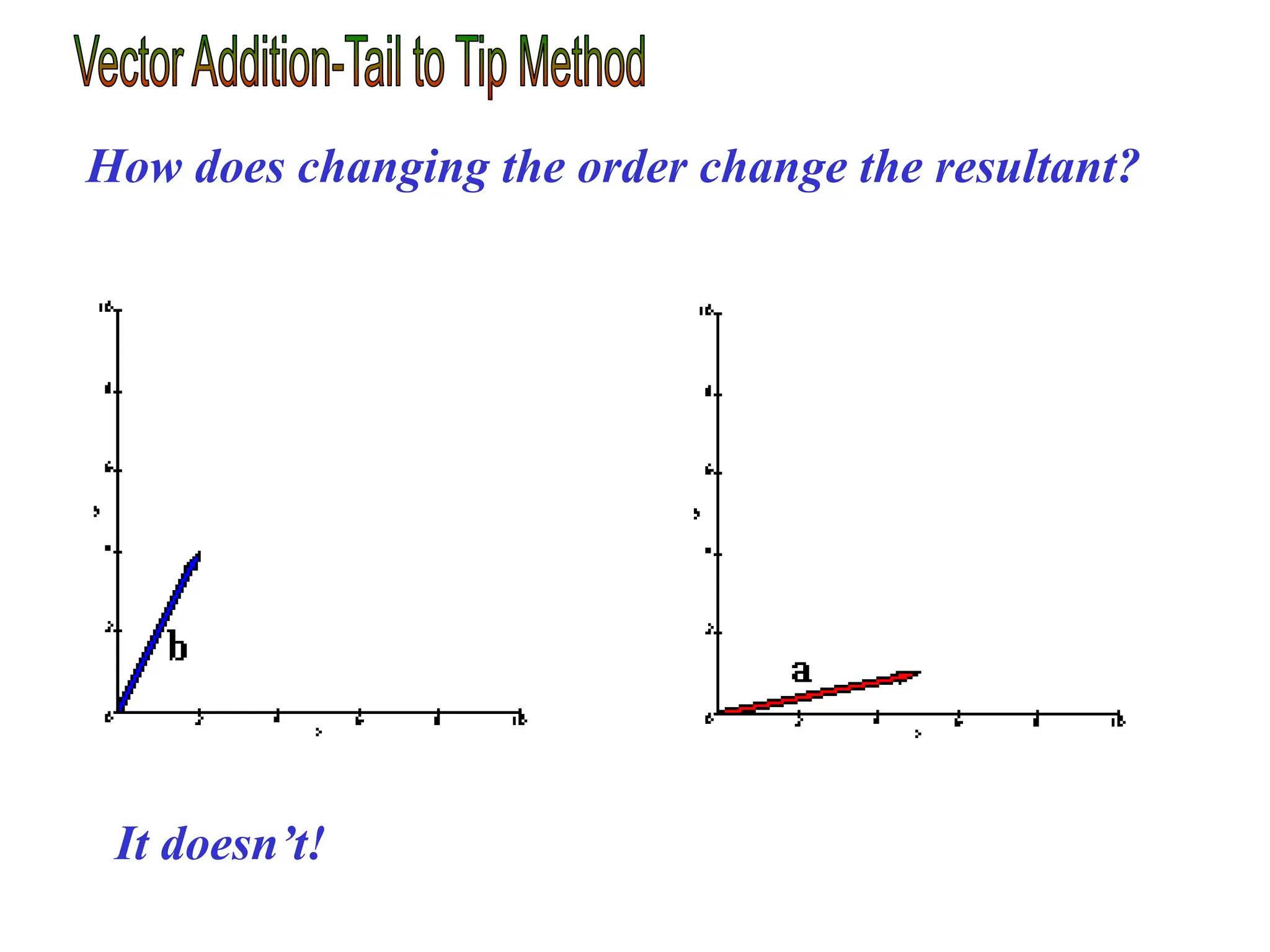
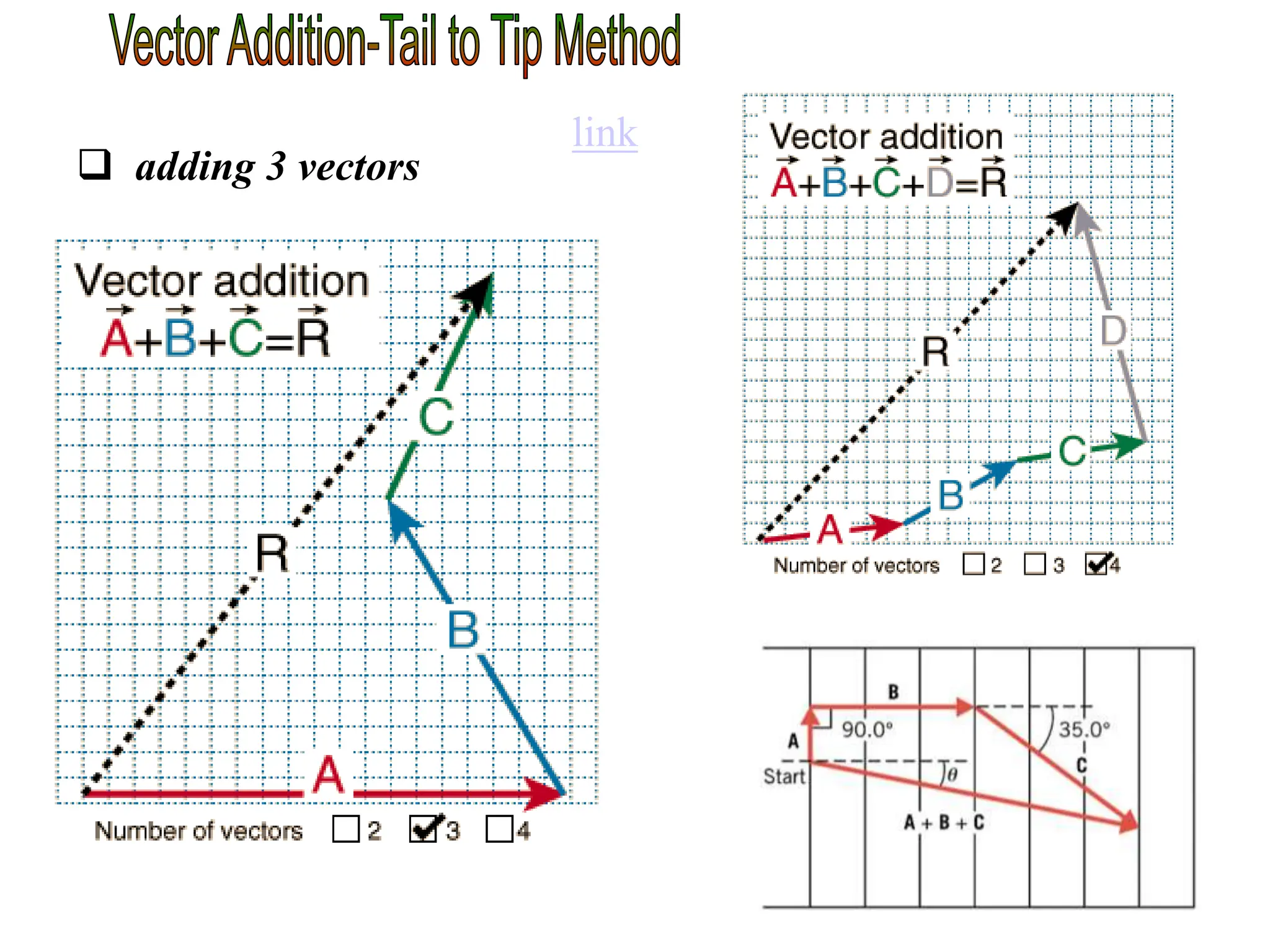
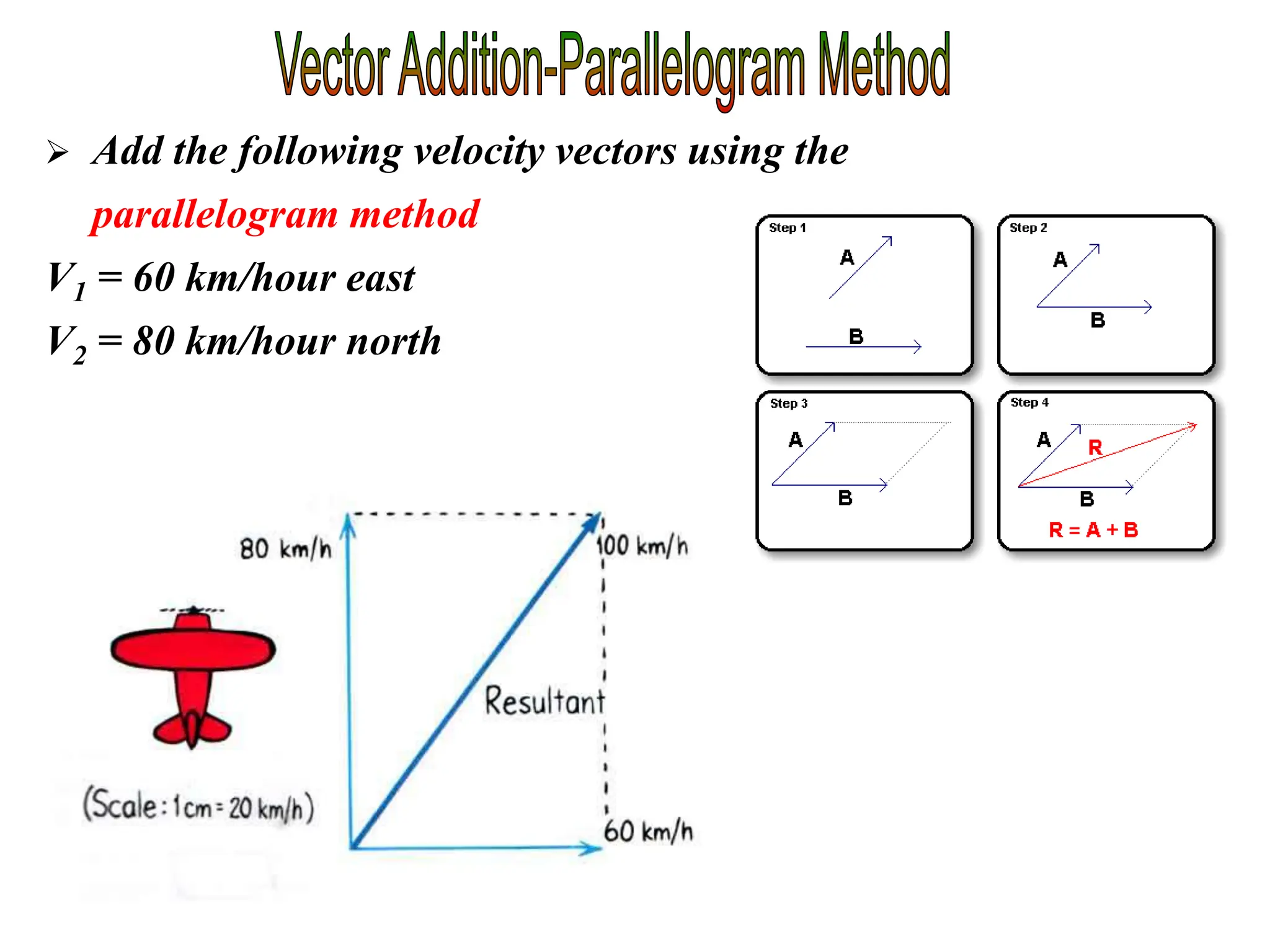
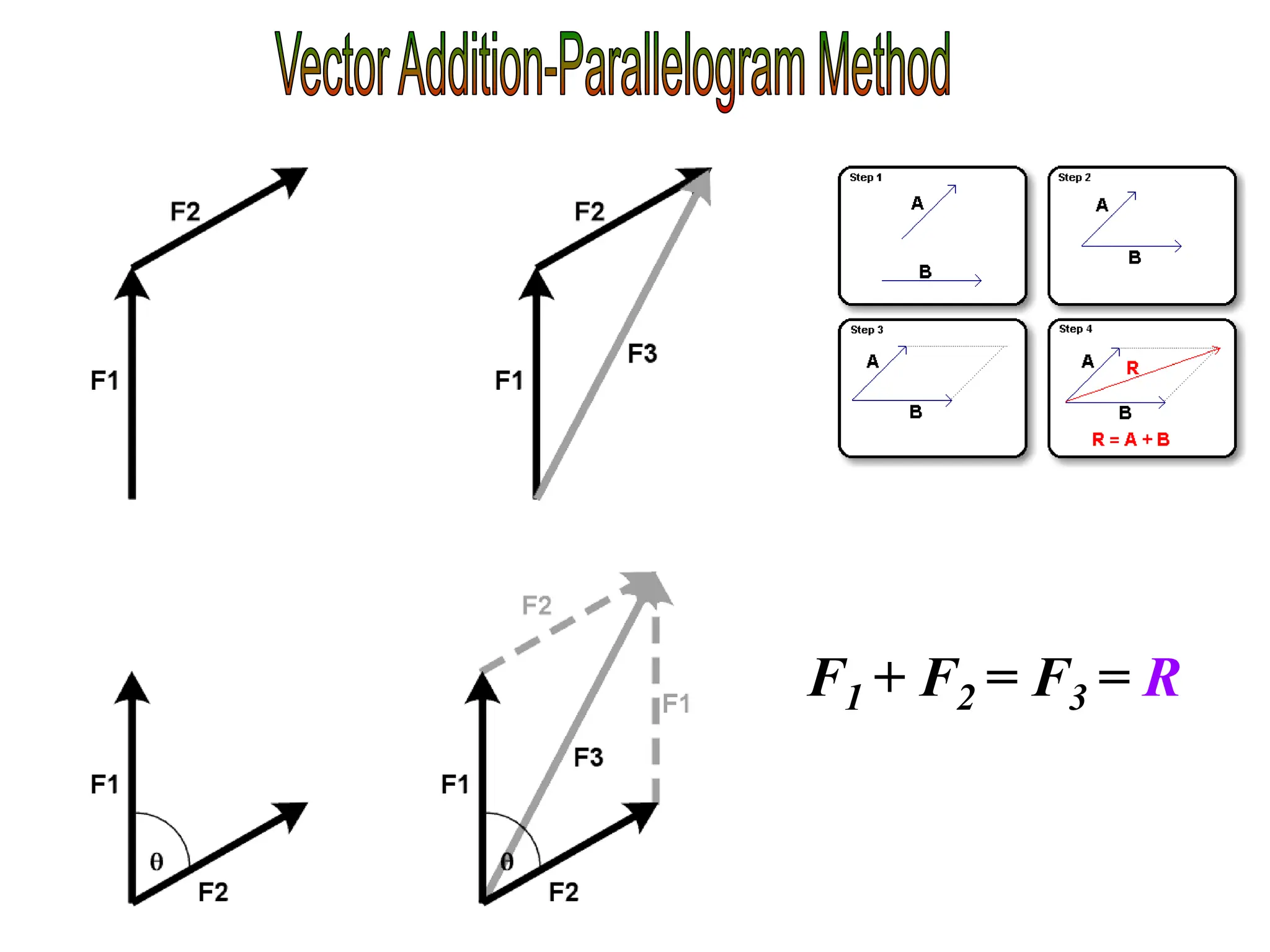
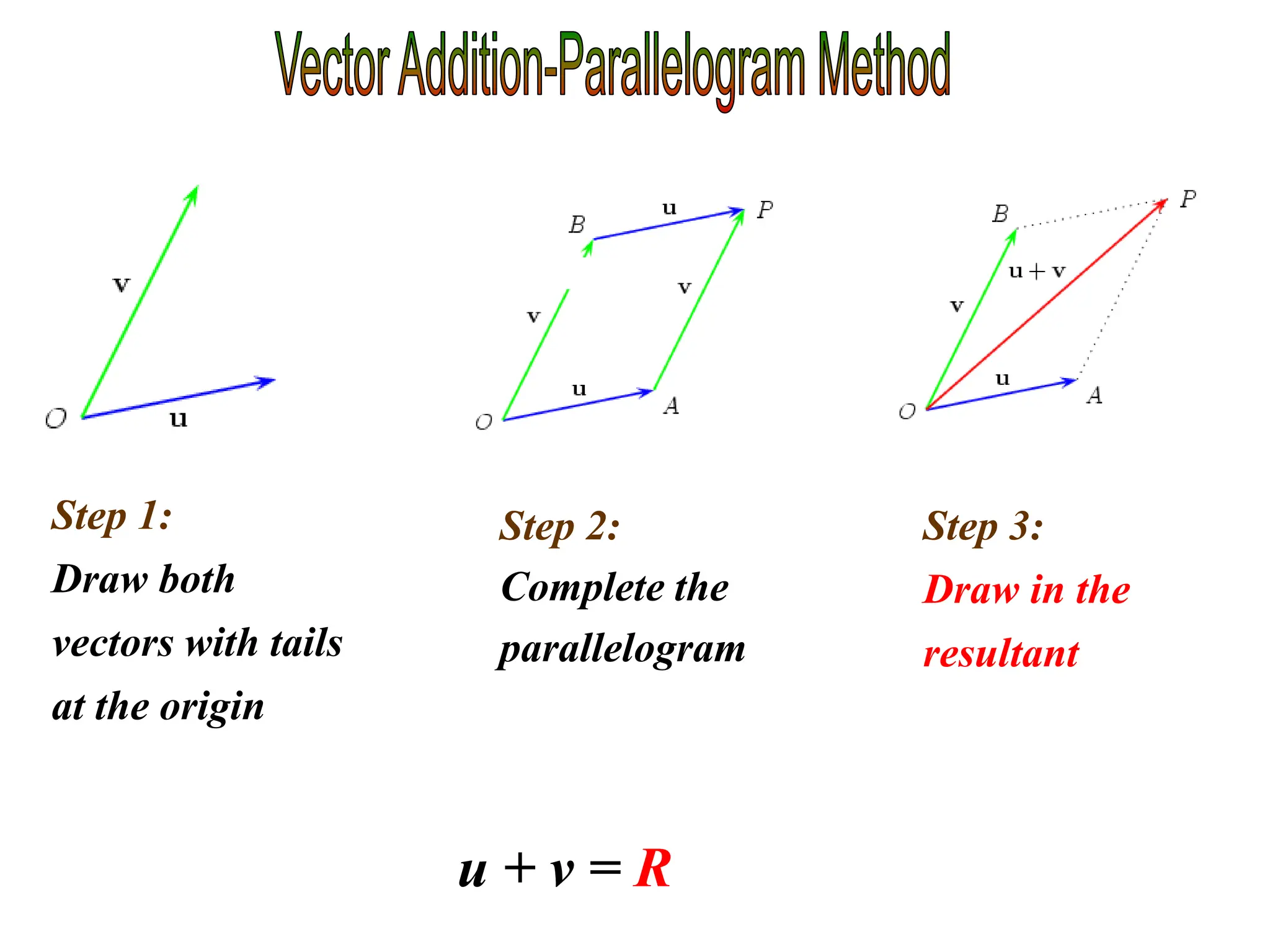
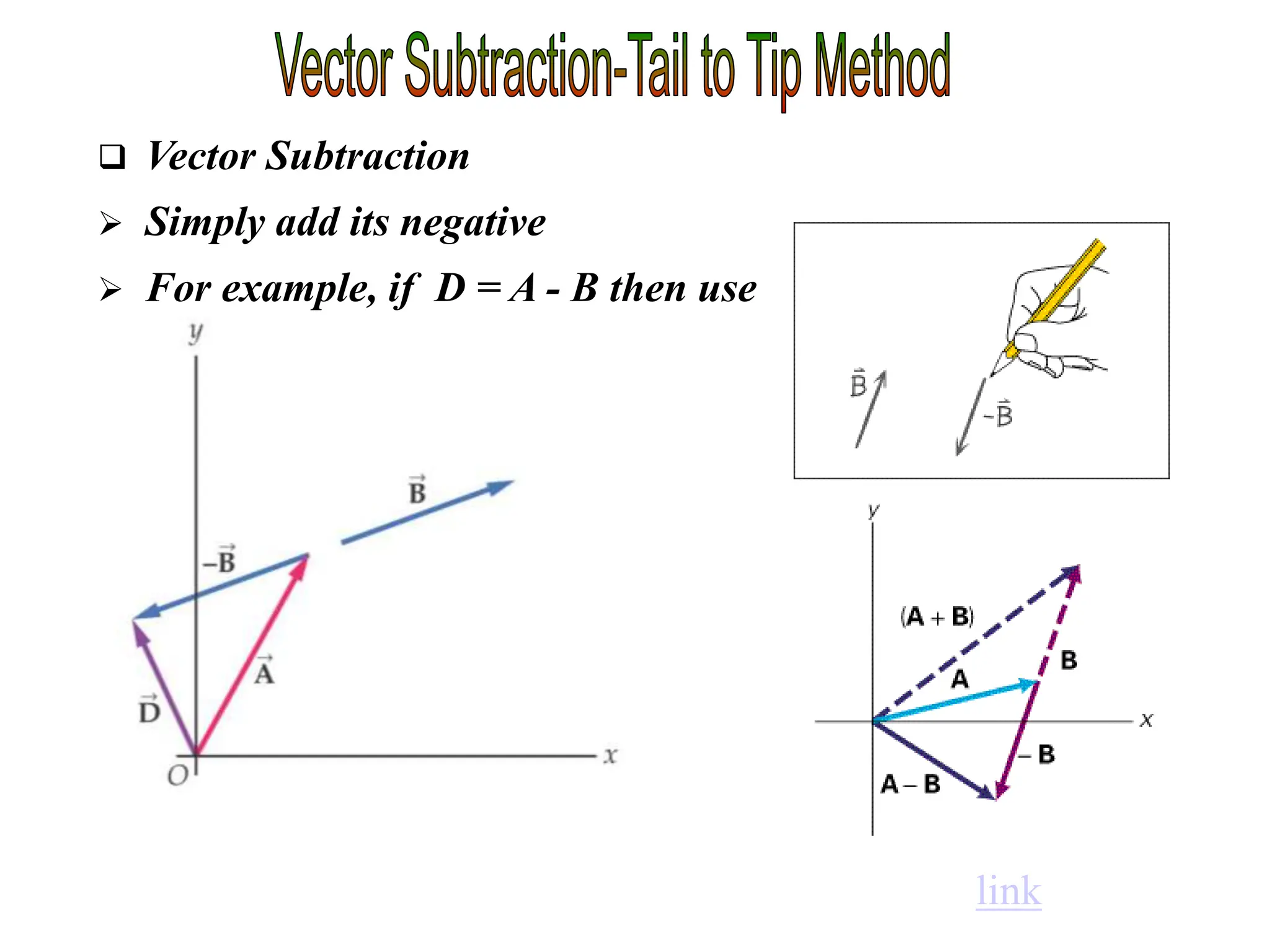
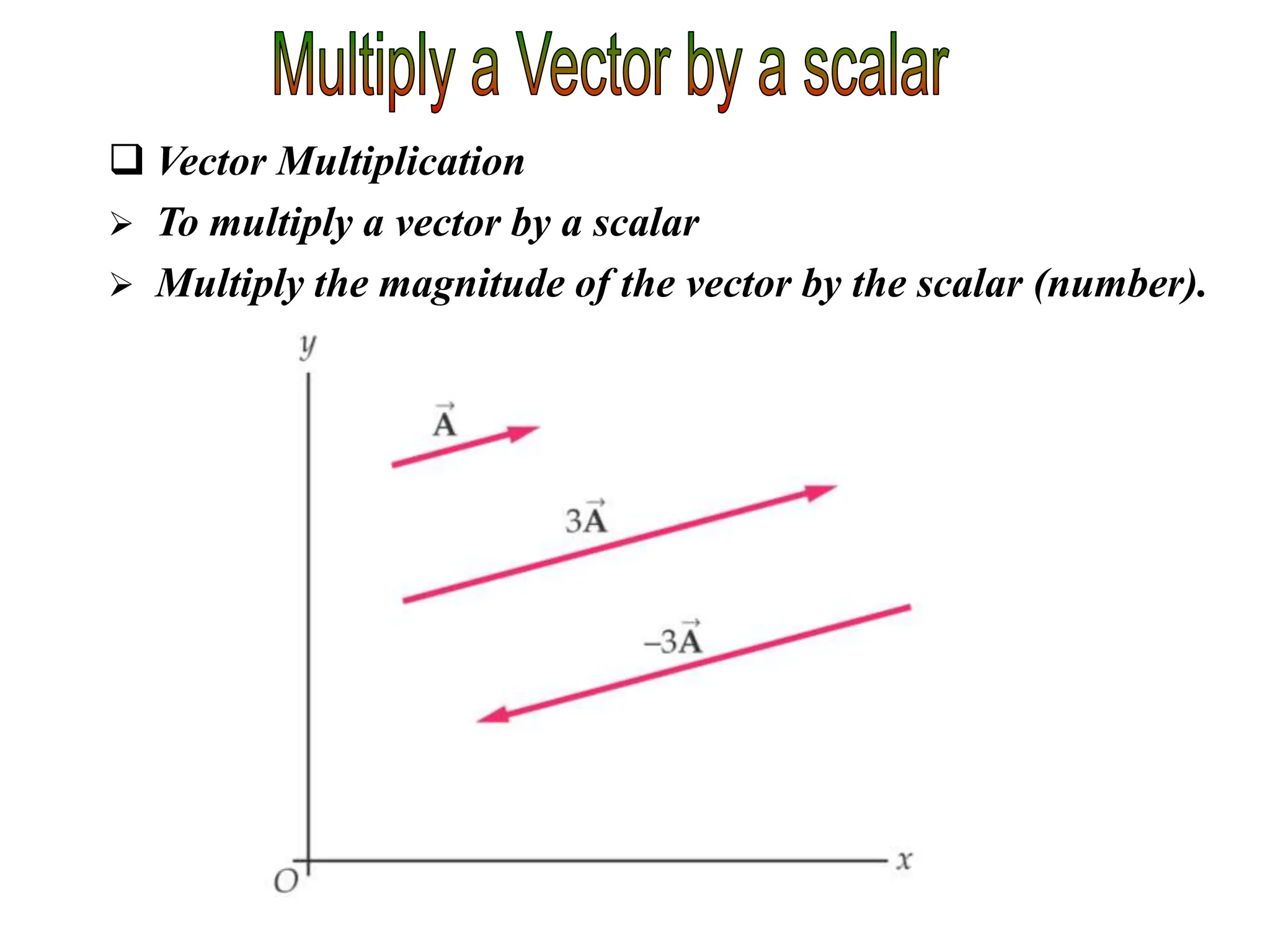
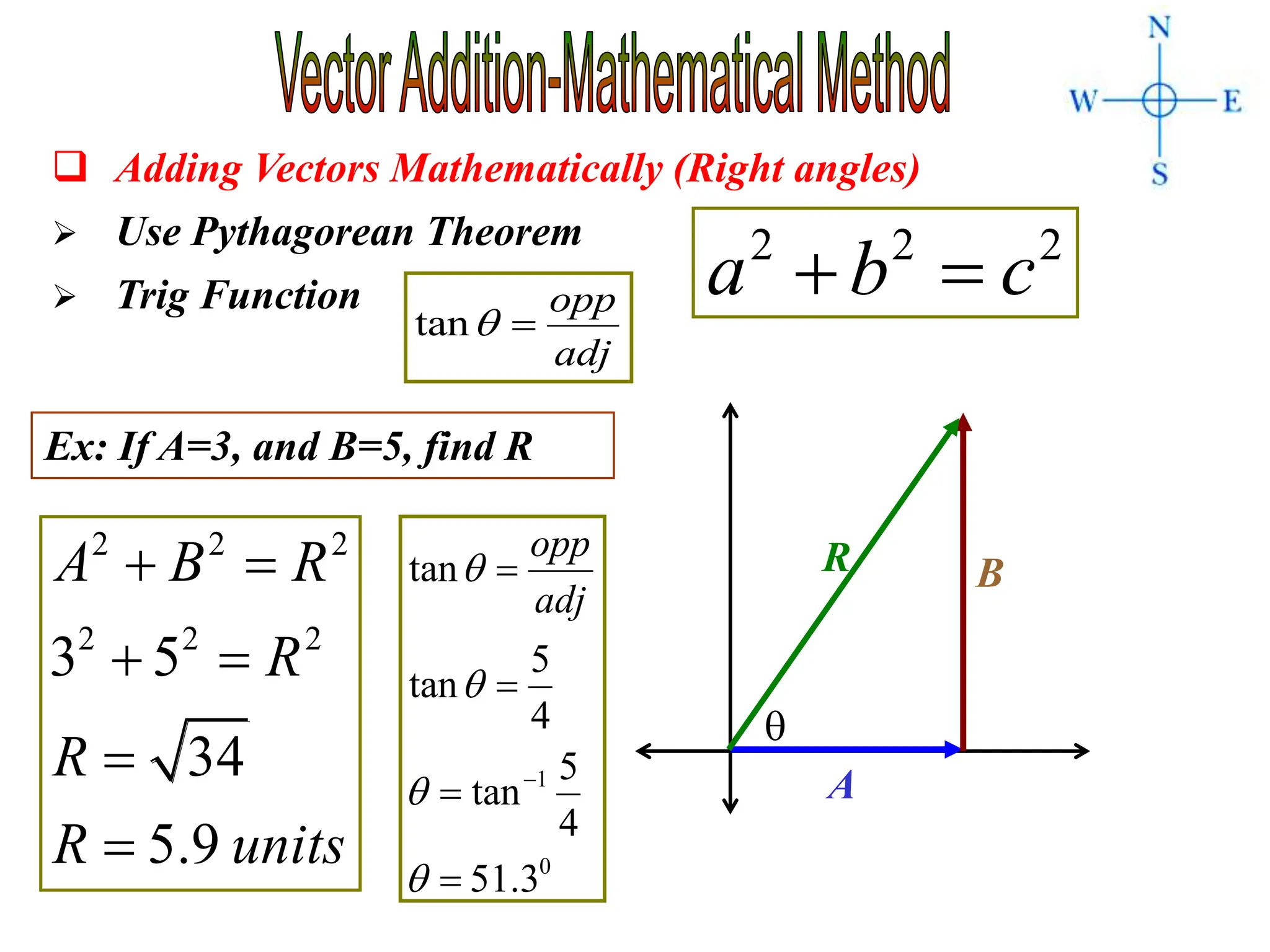
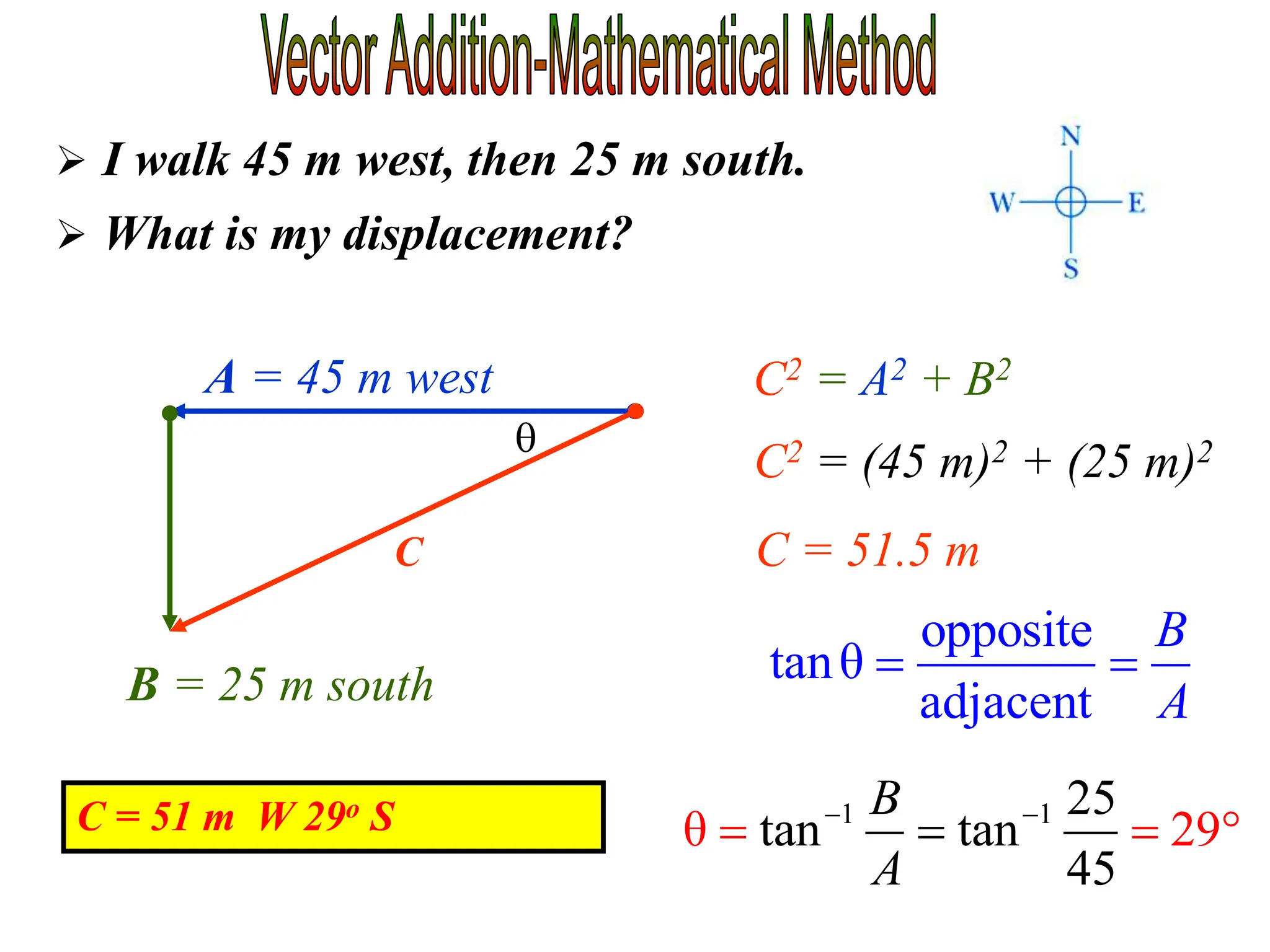
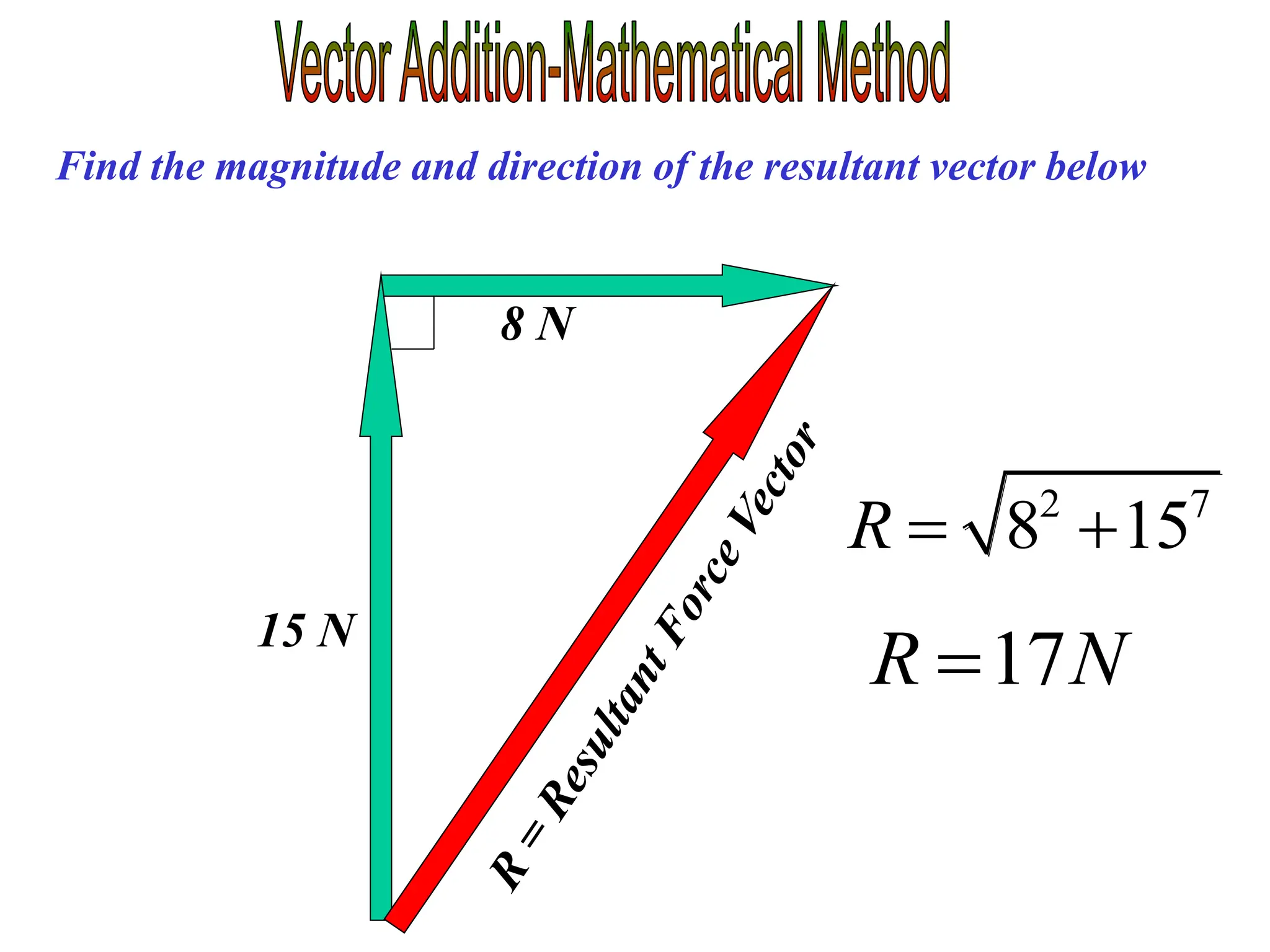
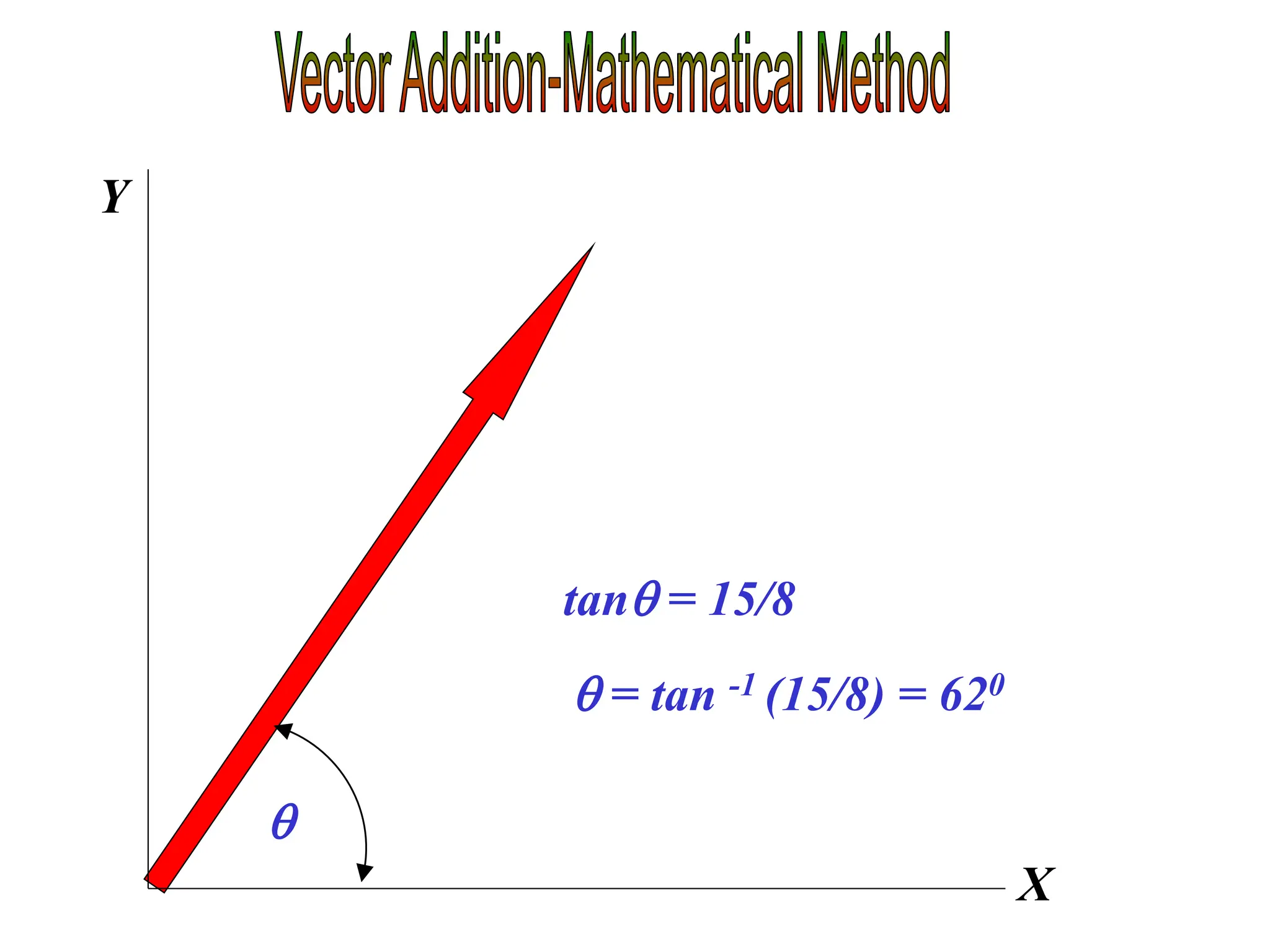
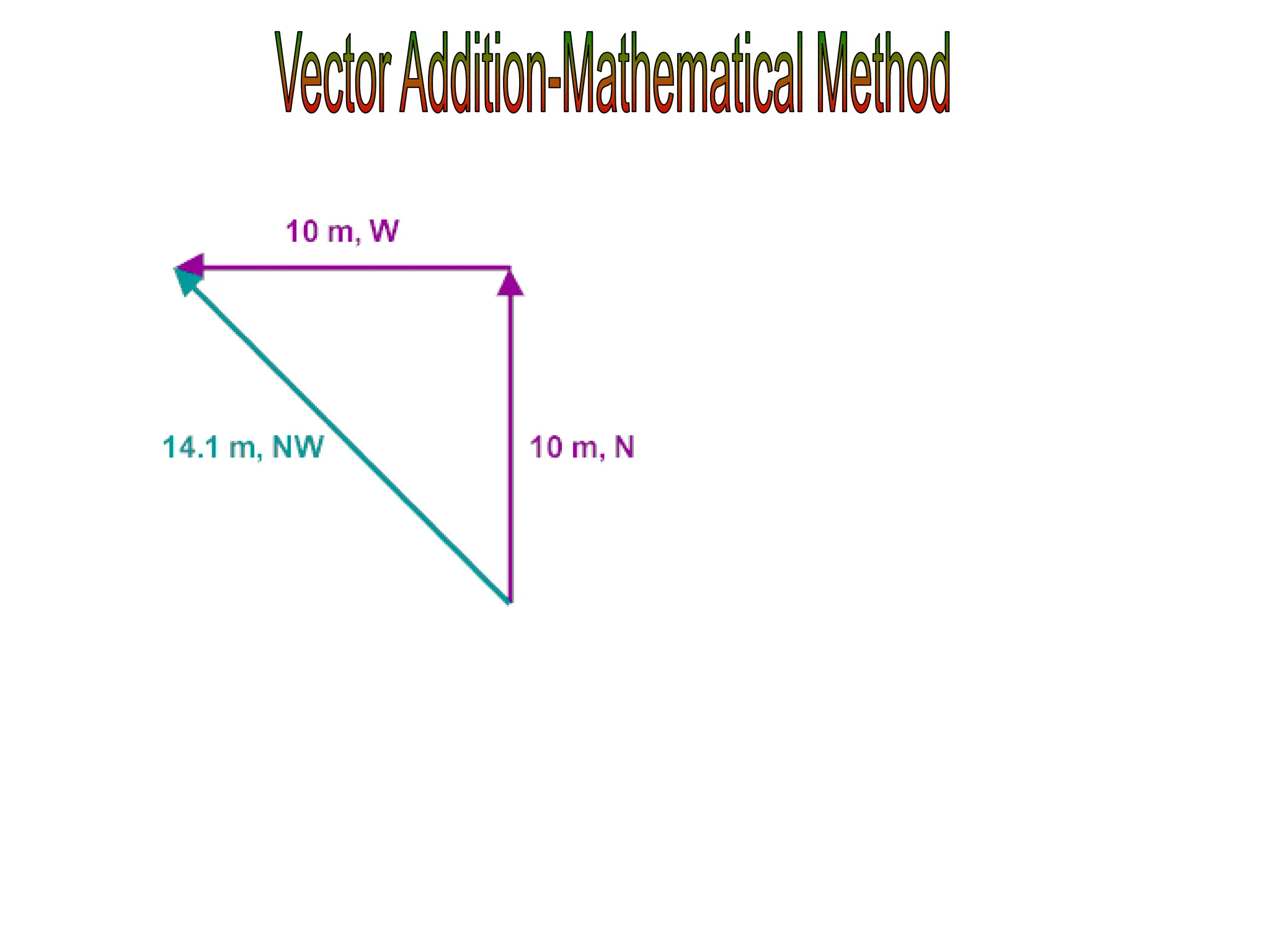
This document discusses scalars and vectors. It defines a scalar as a quantity with only magnitude and a vector as a quantity with both magnitude and direction. Examples of scalars include distance and temperature, while examples of vectors include displacement and velocity. The document also discusses how to represent vectors graphically with arrows and how to add vectors using the tail-to-tip method or parallelogram method, including adding perpendicular and random vectors. It provides examples of how to calculate vector addition and subtraction both graphically and mathematically.

1. I know where I’m
going

2. • A scalar is a quantity described by just a number, usually
with units. It can be positive, negative, or zero.
• Examples:
– Distance
– Time
– Temperature
– Speed
• A vector is a quantity with magnitude and direction. The
magnitude of a vector is a nonnegative scalar.
• Examples:
– Displacement
– Force
– Acceleration
– Velocity

3. Magnitude, what is it?
The magnitude of something is its size.
Not “BIG” but rather “HOW BIG?”

4.  Magnitude and Direction
 When specifying some (not all!) quantities, simply stating its
magnitude is not good enough.
 For example: ”Where’s the library?,” you need to give a vector!
Quantity Category
1. 5 m
2. 30 m/sec, East
3. 5 miles, North
4. 20 degrees Celsius
5. 256 bytes
6. 4,000 Calories

5.  Magnitude and Direction
 Giving directions:
– How do I get to the Virginia
Beach Boardwalk from
Norfolk?
– Go 25 miles. (scalar, almost
useless).
– Go 25 miles East. (vector,
magnitude & direction)

6.  Graphical Representation of Vectors
 Vectors are represented by an arrow.
 The length indicates its magnitude.
 The direction the arrow point determines
its direction.

7. Vector r
 Has a magnitude of 1.5 meters
 A direction of  = 250
 E 25 N

8.  Identical Vectors
 A vector is defined by its magnitude and direction, it
doesn’t depend on its location.
 Thus, are all identical vectors

9.  Properties of Vectors
 Two vectors are the same if their sizes and their
directions are the same, regardless of where they are.
x
y
A
B
E
D
C
F
Which ones are the
same vectors?
A=B=E=D
Why aren’t the others?
C: The same magnitude
but opposite direction:
C= - A
F: The same direction
but different magnitude

10.  The Negative of a Vector
 Same length (magnitude) opposite direction

11. Tail to Tip Method Steps:
i. Draw a coordinate axes
ii. Plot the first vector with the tail at the origin
iii. Place the tail of the second vector at the tip of the first vector
iv. Draw in the resultant (sum) tail at origin, tip at the tip of the
2nd vector. (Label all vectors)
1. Graphically – Use ruler, protractor, and graph paper.
i. Tail to tip method
ii. Parallelogram method
2. Mathematically – Use trigonometry and algebra

12.  2 vectors same direction
Add the following vectors
• d1 = 40 m east
• d2 = 30 m east
• What is the resultant?
d1 = 40 m east d2 = 30 m east
d1 + d2 = 70 m east
Just add, resultant the sum in the same direction.
Use scale 1cm = 10m

13. d1 = 40 m east d2 = 30 m west
d1 + d2 = 10 m east
Subtract, resultant the difference and in the direction of the larger.
 2 vectors opposite direction
Add the following vectors
• d1 = 40 m east
• d2 = 30 m west
• What is the resultant?
Use scale 1cm = 10m

14.  2 perpendicular vectors
Add the following vectors
• v1 = 40 m east
• v2 = 30 m north
• Find R
v1 = 40 m east
v2 = 30 m north
R

1. Measure angle with a protractor
2. Measure length with a ruler
3. Use scale 1cm = 10m
4. R = 50 m, E 370 N

15.  2 random vectors
 To add two vectors together, lay the arrows tail to tip.
 For example C = A + B
link
Use scale 1cm = 10m

16. 1. The magnitude of the resultant vector will be greatest when
the original 2 vectors are positioned how? (00 between them)
2. The magnitude will be smallest when the original 2 vectors
are positioned how? (1800 between them)

17. How does changing the order change the resultant?
It doesn’t!

18. The order in which you add vectors doesn’t effect the resultant.
A + B + C + D + E=
C + B + A + D + E =
D + E + A + B + C
The resultant is the same regardless of the order.

19. link
 adding 3 vectors

20. We cannot just add 20 and 35 to get resultant vector!!
Example: A car travels
1. 20.0 km due north
2. 35.0 km in a direction N 60° W
3. Find the magnitude and direction of the car’s resultant
displacement graphically.
Use scale 1cm = 10km

21. Parallelogram Method Steps:
1. Draw a coordinate axes
2. Plot the first vector with the tail at the origin
3. Plot the second vector with its the tail also at the origin
4. Complete the parallelogram
5. Draw in the diagonal, this is the resultant.
1. Graphically – Use ruler, protractor, and graph paper.
i. Tail to tip method
ii. Parallelogram method
2. Mathematically – Use trigonometry and algebra

22. A
B R
You obtain the same result using either method.
Tail to Tip Method
Parallelogram Method

23.  Add the following velocity vectors using the
parallelogram method
V1 = 60 km/hour east
V2 = 80 km/hour north

24. F1 + F2 = F3 = R

25. u + v = R
Step 1:
Draw both
vectors with tails
at the origin
Step 2:
Complete the
parallelogram
Step 3:
Draw in the
resultant

26.  Vector Subtraction
 Simply add its negative
 For example, if D = A - B then use
link

27.  Vector Multiplication
 To multiply a vector by a scalar
 Multiply the magnitude of the vector by the scalar (number).

28.  Adding Vectors Mathematically (Right angles)
 Use Pythagorean Theorem
 Trig Function
2 2 2
a b c
 
tan
opp
adj
 
A
B
R
2 2 2
2 2 2
3 5
34
5.9
A B R
R
R
R units
 
 


1
0
tan
5
tan
4
5
tan
4
51.3
opp
adj









Ex: If A=3, and B=5, find R


29.  I walk 45 m west, then 25 m south.
 What is my displacement?
A = 45 m west
B = 25 m south
C
C2 = A2 + B2
C2 = (45 m)2 + (25 m)2
C = 51.5 m

opposite
tanθ
adjacent
B
A
 
1 1 25
tan ta 9
5
θ n
4
2
B
A
 
 
 
C = 51 m W 29o S

30. Find the magnitude and direction of the resultant vector below
2 7
8 15
R  
8 N
15 N
17
R N


31. X
Y

tan = 15/8
 = tan -1 (15/8) = 620