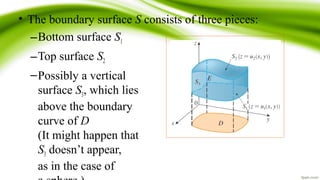
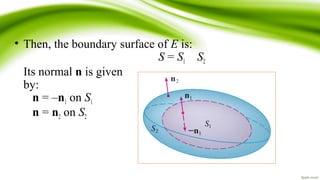
The document summarizes the Divergence Theorem. It states that the theorem relates the integral of the divergence of a vector field F over a region E to the surface integral of F over the boundary S of E. Specifically, the theorem states that the flux of F across S is equal to the triple integral of the divergence of F over E, for a region E that is a simple solid region or a finite union of such regions, and when F has continuous partial derivatives on a region containing E. An example application to computing the flux of a vector field over a unit sphere is also provided.

1. G.H. Patel College of Engineering and
Technology
Subject: Field Theory
Name Enrollment no.
Champaneria Dhvanil J. 150113109004
Chauhan Nisarg D. 150113109005
Jadav Prashant 150113109009
Limbani Milan P. 150113109011

2. Divergence Theorem

3.  The Divergence Theorem
In this section, we will learn about:
The Divergence Theorem for simple solid regions,
and its applications in electric fields and fluid flow.

4.  INTRODUCTION
• In Section 16.5, we rewrote Green’s
Theorem in a vector version as:
• where C is the positively oriented
boundary curve of the plane region D.
div ( , )
C
D
ds x y dA× =∫ ∫∫F n F

5.  INTRODUCTION
• If we were seeking to extend this theorem to
vector fields on, we might make the guess that
• where S is the boundary surface
of the solid region E.
div ( , , )
S E
dS x y z dV× =∫∫ ∫∫∫F n F ……Equation 1

6.  DIVERGENCE THEOREM
• It turns out that Equation 1 is true, under appropriate
hypotheses, and is called the Divergence Theorem.
•Notice its similarity to Green’s Theorem
and Stokes’ Theorem in that:
•It relates the integral of a derivative of a function (div F in
this case) over a region to the integral
of the original function F over the boundary of
the region.

7.  SIMPLE SOLID REGION
• We state and prove the Divergence Theorem for regions E
that are simultaneously of types 1, 2, and 3.
• We call such regions simple solid regions. For instance,
regions bounded by ellipsoids or rectangular boxes are
simple solid regions.
•The boundary of E is a closed surface.
•That is, the unit normal vector n is directed outward from
E.

8.  THE DIVERGENCE THEOREM
• Let:
–E be a simple solid region and let S be
the boundary surface of E, given with positive
(outward) orientation.
–F be a vector field whose component functions
have continuous partial derivatives on an open region
that contains E.
• Then, div
S E
d dV× =∫∫ ∫∫∫F S F

9. • Thus, the Divergence Theorem states that:
–Under the given conditions, the flux of F across the
boundary surface of E is equal to the triple integral of the
divergence of F over E.

10.  THE DIVERGENCE THEOREM
• Let F = P i + Q j + R k
–Then,
–Hence,
div
P Q R
x y z
∂ ∂ ∂
= + +
∂ ∂ ∂
F
Proof
div
E
E E E
dV
P Q R
dV dV dV
x y z
∂ ∂ ∂
= + +
∂ ∂ ∂
∫∫∫
∫∫∫ ∫∫∫ ∫∫∫
F

11. • If n is the unit outward normal of S, then the surface
integral on the left side of the Divergence Theorem is:
( )
S S
S
S S S
d d
P Q R dS
P dS Q dS R dS
× = ×
= + + ×
= × + × + ×
∫∫ ∫∫
∫∫
∫∫ ∫∫ ∫∫
F S F n S
i j k n
i n j n k n

12. • So, to prove the theorem, it suffices to prove these equations:
S E
S E
S E
P
P dS dV
x
Q
Q dS dV
y
R
R dS dV
z
∂
× =
∂
∂
× =
∂
∂
× =
∂
∫∫ ∫∫∫
∫∫ ∫∫∫
∫∫ ∫∫∫
i n
j n
k n
• To prove Equation 4, we use the fact that E is a type 1 region:
where D is the projection of E onto the xy-plane.
( ) ( ) ( ) ( ){ }1 2, , , , , ,
E
x y z x y D u x y z u x y
=
∈ ≤ ≤

13. • By Equation 6 ,we have:
( )( )
( )2
1
,
,
, ,
u x y
u x y
E D
R R
dV x y z dz dA
z z
∂ ∂ 
=  ∂ ∂ 
∫∫∫ ∫∫ ∫
•Thus, by the Fundamental Theorem of Calculus,
( )( ) ( )( )2 1, , , , , ,
E
D
R
dV
z
R x y u x y R x y u x y dA
∂
∂
 = − 
∫∫∫
∫∫

14. • The boundary surface S consists of three pieces:
–Bottom surface S1
–Top surface S2
–Possibly a vertical
surface S3, which lies
above the boundary
curve of D
(It might happen that
S3 doesn’t appear,
as in the case of

15. • Notice that, on S3, we have k ∙ n = 0,
because k is vertical and n is horizontal.
–Thus,
3
3
0 0
S
S
R dS
dS
×
= =
∫∫
∫∫
k n
• Thus, regardless of whether there
is a vertical surface, we can write:
1 2S S S
R dS R dS R dS× = × + ×∫∫ ∫∫ ∫∫k n k n k n

16. • The equation of S2 is z = u2(x, y), (x, y) D, and the outward
normal n points upward.
–So, from Equation 10
(with F replaced by
R k), we have:
( )( )
2
2, , ,
S
D
R dS
R x y u x y dA
× =∫∫
∫∫
k n
•On S1, we have z = u1(x, y).
•However, here, n points downward.
• So, we multiply
by –1:
( )( )
1
1, , ,
S
D
R dS
R x y u x y dA
× =
−
∫∫
∫∫
k n

17. • Therefore, Equation 6 gives:
( )( ) ( )( )2 1, , , , , ,
S
D
R dS
R x y u x y R x y u x y dA
×
 = − 
∫∫
∫∫
k n
•Comparison with Equation 5 shows that:
•Equations 2 and 3 are proved in a similar manner using the
expressions for E as a type 2 or type 3 region, respectively.
S E
R
R dS dV
z
∂
× =
∂∫∫ ∫∫∫k n

18. • Find the flux of the vector field
F(x, y, z) = z i + y j + x k
over the unit sphere
x2
+ y2
+ z2
= 1
–First, we compute the divergence of F:
 Example 1
( ) ( ) ( )div 1z y x
x y z
∂ ∂ ∂
= + + =
∂ ∂ ∂
F

19. • The unit sphere S is the boundary of the unit ball B given by:
x2
+ y2
+ z2
≤ 1
–So, the Divergence Theorem gives the flux
as:
( ) ( )
34
3
div 1
4
1
3
S B B
F dS dV dV
V B
π
π
× = =
= = =
∫∫ ∫∫∫ ∫∫∫F

20.  UNIONS OF SIMPLE SOLID REGIONS
• The Divergence Theorem can also be proved for regions
that are finite unions of simple solid regions.
•For example, let’s consider the region E that lies between the closed surfaces S1 and
S2, where S1 lies inside S2.
•Let n1 and n2 be outward normal
of S1 and S2.

21. • Then, the boundary surface of E is:
S = S1 S2
Its normal n is given
by:
n = –n1 on S1
n = n2 on S2

22. • Applying the Divergence Theorem to S, we get:
( )
1 2
1 2
1 2
div
E S
S
S S
S S
dV d
dS
dS dS
d d
= ×
= ×
= × − + ×
= − × + ×
∫∫∫ ∫∫
∫∫
∫∫ ∫∫
∫∫ ∫∫
F F S
F n
F n F n
F S F S

23. Thank you…..