1) Vectors are quantities that have both magnitude and direction, unlike scalars which only have magnitude. Common vector quantities include force, velocity, and displacement. 2) Vectors can be described by their magnitude, direction, and reference frame. Direction is measured in degrees from the x-axis. 3) Vector operations like addition, subtraction, multiplication and division can be performed graphically or using components and trigonometry. Parallel vectors can be added/subtracted algebraically but others require using components. 4) To add vectors using components, each vector is broken into x and y components using trigonometry. The x and y components can then be added separately and combined to find the overall resultant vector.

1. LECTURE 1
VECTORS
IB Physics Power Points
Topic 2
Kinematics
www.pedagogics.ca

2. Sections of Lecture 1
• What is a vector?
• Describing vectors
• Multiplication and Division of vectors
• Addition and Subtraction of Vectors
• Vectors in same or opposite directions
• Vectors at right angles
• All other vectors

3. What is a vector?
Vectors are quantities that have magnitude (size)
AND direction.
For example:
35 m is a scalar quantity.
35 m [East] is a vector quantity.
Quantities like temperature, time, mass and
distance are examples of scalar quantities.
Quantities like force, velocity, and displacement
are examples of vector quantities.

4. Describing Vectors
Consider a gravitational force of 65 N [down]
magnitude unit direction
Vectors are graphically represented by arrows:
Length = magnitude
Drawn to scale
F

5. When describing vectors, it is convenient to
use a standard (x,y) reference frame.
+ y direction
North
up
- y direction
South
down
- x direction
West
left
+x direction
East
right

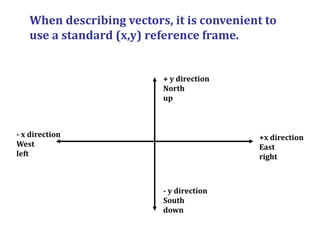
6. In physics, convention dictates vector direction
(angle) is measured from the x axis of the frame of
reference.
+ y direction
North
up
- y direction
South
down
- x direction
West
left
+x direction
East
right
30o
S
[right, 30o above horizontal]
[30o N of E]
[E, 30o upwards]

7. In math it is common to describe direction differently:
For example:
To a physicist, the direction of
this vector is [60o S of W]
OR . . . measure the angle of
direction in a counter clockwise
direction from East. The same
vector direction is now described as
[240o] This method has advantages.

8. Multiplication and Division with Vectors
Any vector can be multiplied or divided by a
scalar (regular) number.
The multiplication or division will change the
magnitude of the vector quantity but not the
direction.
For example:
F 2F

9. Addition and Subtraction of Vectors
Part 1: Parallel vectors
Example 1: Blog walks 35 m [E], rests for 20 s and
then walks 25 m [E]. What is Blog’s overall
displacement? (what is displacement??)
Solve graphically
by drawing a scale
diagram.
1 cm = 10 m
Place vectors head to
tail and measure
resultant vector.
1s
 2s
  60 m [E]s

10. Solve algebraically by adding the two magnitudes.
WE CAN ONLY DO THIS BECAUSE THE VECTORS ARE
IN THE SAME DIRECTION.
SO 35 m [E] + 25 m [E] = 60 m [E]
Solve Graphically
1 2x x
1x
 2x
  10 m [E]x
Example 2: Blog walks 35 m [E], rests for 20 s and
then walks 25 m [W]. What is Blog’s overall
displacement?
resultant

11. Algebraic solution, we can still add the two
magnitudes. WE CAN ONLY DO THIS BECAUSE THE
VECTORS ARE PARALLEL!
WE MUST MAKE ONE VECTOR NEGATIVE TO
INDICATE OPPOSITE DIRECTION.
SO 35 m [E] + 25 m [W]
= 35 m [E] + – 25 m [E]
= 10 m [E]
Note that 25 m [W] is the same as – 25 m [E]

12. Addition and Subtraction of Vectors
Part 2: Perpendicular Vectors
Example 3: Blog walks 30 m [N], rests for 20 s and
then walks 40 m [E]. What is Blog’s overall
displacement?
Solve Graphically
1 2x x
1x
 2x
length 50 m
37o
 
  o
x 50 m [37 N of E]

13. Addition and Subtraction of Vectors
Part 2: Perpendicular Vectors
Algebraic solution: use trigonometry.
Diagram does not need
to be to scale.
  2 2
30 40 50 mx
1x
 2x
  o
x 50 m [37 N of E]
1 1 30
tan tan 37
40
oy
x
   
    
 


14. Part 3 - Adding multiple vectors (method of components)
Consider the following 3 displacement vectors:
A student walks
3 m [45o N of E]
6 m [N]
5 m [30o N of W]
Vectors are illustrated here to scale.
To determine the resultant displacement, add the
individual vectors graphically by drawing them head to
tail.

15. The resultant displacement is 11 m [102o] OR 11 m [78o N of W]
Show scale diagram solution here

16. + x direction
West
left
It is not possible to add
the vectors shown in the
diagram by the algebra
methods discussed
previously. The vectors
are neither parallel or
perpendicular.

17. Method of Components
To add vectors that are not in the same or perpendicular
directions – use method of components.
All vectors can be described in terms of two components
called the x component and the y component.
This is a
displacement
vector of
magnitude 36 m
The vector has
been placed on an
x,y coordinate axis
with the tail at the
origin (0,0)

18. Method of Components
The x component of this vector is shown by the green line.
The y component of this vector is shown by the pink line.
x
y

19. Method of Components
You may have noticed that the original vector is just the sum
of the two vector components
x
y
+
36 m [34o N of E]
There is NO
difference in
displacement
between walking
36 m [34o N of E]
and walking x m
[E] followed by y m
[N]

20. Now consider this vector
18 m [45o S of E]
36 m [34o N of E]
Graphically added
to a second vector
Resultant
We can’t use algebra to add
these vectors directly BUT
we could use algebra to add
their components.

21. 18 m [45o S of E]
x1
y1
36 m [34o N of E]
To get the same resultant
x2
y2
x1 x2
y1
y2

22. Conclusion: Adding the vectors
graphically using their components
produces the same result.
BONUS: Components can be added using
math methods because all x components
are in the same plane as are all y
components. Furthermore, x and y
components are perpendicular and can be
added to each other using Pythagorean
theorem.
It really is
elementary!
Now you need
to meet my old
Greek friend

23. Meet Hipparchus,
considered to be the father
of trigonometry.
He is here to remind you of
our fictitious Mayan hero
Chief Soh Cah Toa

adjacent
opposite

24. Determining Components
The x component = S (cos )
The y component = S (sin )
x
y

S
sin
cos
y
S
x
S
 
   
 
 
   
 
Where S is the magnitude of the original vector and
 is the angle between the original vector and the x axis

25. Examples:
Resolve the following vectors into x and y components
Vector X Y
15.2 m [27o N of E]
12.7 ms-1 [56o]
45.0 N [48o N of W]
725 m [205o] -657 m -306 m
7.1 ms-1 10.5 ms-1
13.5 m 6.90 m
-30.1 N 33.4 N

26. Solving vector problems
Example: Blog starts his walk at the old oak tree.
He walks 55 m [42o S of E] to Point A. He then
walks 75 m [185o] to Point B. He then walks a final
62 m [78o N of W] to Point C. What is Blog’s overall
displacement?
Step 1 (always)
Sketch a diagram
(does not have to be to
scale but it helps) A
B
C

27. Solving vector problems
Step 2: Resolve vectors into x and y components
and add them.
Vector X Y
55 m [42o S of E] 40.9 -36.8
75 m [185o] -74.7 -6.54
62 m [78o N of W] -12.9 60.6
55cos(42) 75cos(185) 62cos(78)
40.9 74.7 12.9
46.7
x x x x
x
x
x
s A B C
s
s
s
  
  
  
 





28. Solving vector problems
Step 2: Resolve vectors into x and y components
and add them.
Vector X Y
55 m [42o S of E] 40.9 -36.8
75 m [185o] -74.7 -6.54
62 m [78o N of W] -12.9 60.6
55sin(42) 75sin(185) 62sin(78)
36.8 6.54 60.6
17.3
y y y y
y
y
y
s A B C
s
s
s
  
   
   






29. Solving vector problems
Step 3: Use sum of components to determine
resultant.
Sx = -46.7 m OR 46.7 m [W]
Sy = 17.3 m or 17.3 m [N]
Sy = 17.3 m
Sx = - 46.7 m
Use trig to find length and
direction of resultant.
49.8 m [20.3o N of W]