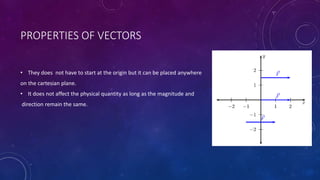
This document discusses calculating the resultant of perpendicular vectors. It defines scalar and vector quantities, with examples. It explains that vectors have both magnitude and direction, while scalars only have magnitude. The document then presents two methods for finding the resultant of perpendicular vectors: 1) the tail-to-head method, which draws the second vector from the tip of the first, and 2) the parallelogram method, which forms a rectangle using the vectors and takes the resultant as the diagonal. The document concludes with an activity asking the reader to apply these methods to find the resultant of a 3N rightward force and 5N downward force.

1. RESULTANT OF
PERPENDICULAR VECTOR
GRADE 11
PRESENTED BY: SEANEGO JK
14 May 2020

2. RECAP
• What are scalar and vector quantities and what
are their examples?

3. RESULTANT OF PERPENDICULAR VECTOR
• Vector is a physical quantity with both direction and magnitude( e.g.: force,
velocity, displacement etc.)
• A scalar is a physical quantity with only the magnitude ( e.g.: mass, time,
temperature etc.)

4. PROPERTIES OF VECTORS
• They does not have to start at the origin but it can be placed anywhere
on the cartesian plane.
• It does not affect the physical quantity as long as the magnitude and
direction remain the same.

5. REPRESENTING THE RESULTANT OF CO-LINEAR
FORCES/VECTORS
• Two persons are lifting a heavy box by pulling it upwards using two ropes. The total vertical pulling force is the
combined pulling force of the two men
• A vector is represented by arrows drawn to scale
• There are different ways of indicating direction of a vector
a) Points of a compass
b) 2. Bearing: the angle is measured in a clockwise direction from a south to north base line. This vertical base
line is taken a 0°.
c) The angle made to a given direction or point of reference ( e.g. 50° east of north or 50° E of N)
• Displacement – a straight line drawn from the starting point to the ending point indicating both magnitude
and directions
• Resultant-(R) (vector sum) of a number of vectors is that single vectors which will have the same effect as the
original vectors acting together

6. PHET SIMULATION
• https://phet.colorado.edu/sims/html/vector-addition/latest/vector-addition_en.html

7. METHODS TO CALCULATE RESULTANT OF TWO
FORCES
Method 1 :graphical representation- Tail to Head
• choose a suitable scale e.g. 10mm = 10 N
• Accurately draw the first vector as an arrow according to the chosen scale and in the correct
direction
• draw the second accurate vector by placing the tail of the second vector at the tip of the first
vector
• complete the diagram by drawing (the resultant) a straight line from the tail of the first vector
to the head of the second vector
• measure the length and direction of the resultant vector. Use the scale to determine the actual/ real
magnitude of the resultant. Use the protractor to measure the angle of the resultant
Rx=300N
Ry=40
R=500N
α=50.2°

8. DEMONSTRATION OF METHOD 1:
HTTPS://WWW.YOUTUBE.COM/WATCH?V=2EJSNXYNWVU

9. METHOD 2: PARALLELOGRAM METHOD
• choose an accurate scale e.g. 10mm = 10 N
• accurately draw the first vector as an arrow according to the chosen scale and in the correct direction (
east)
• draw the second accurate vector by placing the tail of the second vector on the tail of the first vector
and in the correct direction( south)
• Form a rectangle by drawing two lines parallel to Rx and Ry respectively and with the same length
• Lastly draw R being a diagonal line starting from the tails of RX and RY
Ry=400N
Rx=300N
R=500N

10. DEMONSTRATION OF METHOD 2
HTTPS://WWW.YOUTUBE.COM/WATCH?V=RQFYBU5KVJK

11. SUMMARY OF THE LESSON
• vectors do not have to start at the origin
• use arrows, compass, bearings and point of reference for vector direction
• we can use tail-to-head and parallelogram method to find resultant vector

12. ACTIVITY
• Two forces are applied to an object : 3 N to the right and 5 N downwards. Sketch the forces on the
Cartesian plane and draw the resultant force using these methods
• 1. Tail to head method
• 2. Parallelogram method